Связь поверхностного интеграла 2-го рода с интегралом 1-го рода.
Теорема Гаусса-Остроградского. Соленоидальное поле. Дивергенция
1. Поверхностный интеграл 2-го рода. Поток векторного поля
Будем рассматривать гладкие двусторонние поверхности. Сторона выбирается с помощью нормали к поверхности.
Пусть  некоторая двусторонняя поверхность,
некоторая двусторонняя поверхность,  - векторное поле на поверхности
- векторное поле на поверхности  . Нам необходимо определить поверхностный интеграл второго рода по какой-то стороне поверхности
. Нам необходимо определить поверхностный интеграл второго рода по какой-то стороне поверхности  для векторного поля
для векторного поля  . Этот интеграл запишется следующим образом:
. Этот интеграл запишется следующим образом:
 .
.
Определим интеграл  . Остальные интегралы будут определяться аналогично.
. Остальные интегралы будут определяться аналогично.
Пусть  . Стороны на этой поверхности можно выбирать следующим образом:
. Стороны на этой поверхности можно выбирать следующим образом:
 - это сторона поверхности, нормаль к которой образует с осью
- это сторона поверхности, нормаль к которой образует с осью  острый угол;
острый угол;
 - это сторона поверхности, нормаль к которой образует с осью
- это сторона поверхности, нормаль к которой образует с осью  тупой угол.
тупой угол.
В таком случае положим
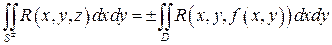 .
.
Физический смысл поверхностного интеграла 2-го рода – вычисление потока векторного поля  через поверхность
через поверхность  в направлении нормали
в направлении нормали 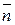 .
.
2. Связь поверхностного интеграла 2-го рода с интегралом 1-го рода
Имеем
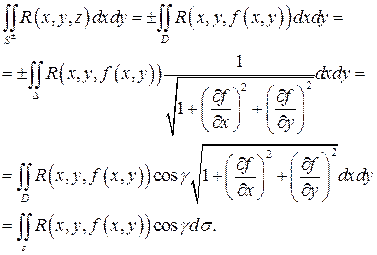
Отсюда
 .
.
3. Теорема Гаусса-Остроградского
Пусть  замкнутая поверхность с внешней нормалью
замкнутая поверхность с внешней нормалью 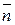 к.
к.  - тело, ограниченное этой поверхностью,
- тело, ограниченное этой поверхностью, 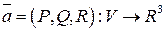 .
.
Тогда имеет место следующая теорема.
Теорема ( теорема Гаусса - Остроградского). Справедливо равенство:

где
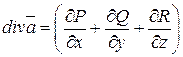 - дивергенция поля
- дивергенция поля 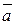 .
.
Доказательство. Имеем  ,
,
 .
.
Поэтому достаточно доказать следующие равенства:
 ,
,  ,
, 
Пусть  . Тогда
. Тогда

Далее


Аналогично  ,
,  .
.
Теорема доказана.
Из теоремы Гаусса – Остроградского вытекает важная в приложениях вторая формула Грина.
Пусть 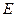 - пространственное тело, ограниченное кусочно-гладкой поверхностью
- пространственное тело, ограниченное кусочно-гладкой поверхностью  . На поверхности
. На поверхности  выбрана сторона с помощью внешней нормали. В теле
выбрана сторона с помощью внешней нормали. В теле 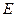 заданы два гладких векторных поля
заданы два гладких векторных поля  и
и  . В этих предположениях выполняется утверждение.
. В этих предположениях выполняется утверждение.
Теорема (вторая формула Грина) Справедливо следующее равенство
 ,
,
где  - производная
- производная  по направлению внешней нормали
по направлению внешней нормали  .
.
Доказательство. Имеем
 .
.
Согласно теоремы Гаусса - Остроградского

где поверхностные интегралы второго рода взяты по внешней стороне поверхности  , ограничивающей область
, ограничивающей область  . Пусть
. Пусть 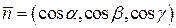 . Тогда поверхностные интегралы второго рода в правых частях могут быть записаны как поверхностные интегралы первого рода:
. Тогда поверхностные интегралы второго рода в правых частях могут быть записаны как поверхностные интегралы первого рода:

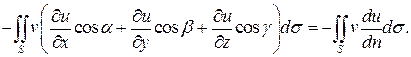
Окончательно получим 
4. Соленоидальное поле. Дивергенция
Векторное поле  в области
в области  называется соленоидальным, если для любого замкнутой поверхности
называется соленоидальным, если для любого замкнутой поверхности  поток через нее равен нулю. Из теоремы Гаусса – Остроградского вытекает следующее утверждение.
поток через нее равен нулю. Из теоремы Гаусса – Остроградского вытекает следующее утверждение.
Теорема. Следующие условия эквивалентны:
1) Поле  - соленоидальное в E;
- соленоидальное в E;
2)  в области E;
в области E;
3) существует векторное поле  .
.
ЛЕКЦИЯ 11
Формула Стокса. Условия независимости криволинейного интеграла 2-го рода от пути в R3. Потенциальное поле. Циркуляция. Ротор
1. Формула Стокса
Пусть 

 - двусторонняя поверхность
- двусторонняя поверхность
 .
.
Тогда множество  - граница (или край) поверхности S.
- граница (или край) поверхности S.
Теорема (Формула Стокса ). Если ориентации на  и
и  согласованы, то
согласованы, то

Доказательство. Необходимо доказать равенство

или три равенства

Для простоты докажем первое равенство в предложении, что поверхность
 .
.
Имеем










Что и требовать показать.
3. Потенциальное поле. Циркуляция. Ротор
Векторное поле  называется потенциальным, если существует скалярное поле
называется потенциальным, если существует скалярное поле  - потенциал такой, что
- потенциал такой, что 
т.е.  есть решение системы
есть решение системы 
Циркуляцией векторного поля  вдоль замкнутой кривой L называется криволинейный интеграл второго рода
вдоль замкнутой кривой L называется криволинейный интеграл второго рода

В случае, когда векторное поле  является силовым полем, циркуляция даёт величину работы этого поля вдоль кривой L.
является силовым полем, циркуляция даёт величину работы этого поля вдоль кривой L.
Ротором (или вихрем) дифференцируемого векторного поля  называется вектор
называется вектор
 .
.
2. Условия независимости криволинейного интеграла 2-го рода от пути в R 3
Лемма. Работа векторного поля  в области
в области  не зависит от пути, а зависит только от начала и конца пути
не зависит от пути, а зависит только от начала и конца пути  любая циркуляция в E равна 0.
любая циркуляция в E равна 0.
Доказательство. Точно такое же, как в плоском случае.
Теорема. Следующие условия эквивалентны:
1) поле  потенциальное, в односвязной области E;
потенциальное, в односвязной области E;
2) ротор  в области E;
в области E;
3) работа поля  в E не зависит от пути.
в E не зависит от пути.
Доказательство. Будем следовать схеме 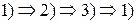 .
.
 :
: 


 .
.
 Имеем
Имеем


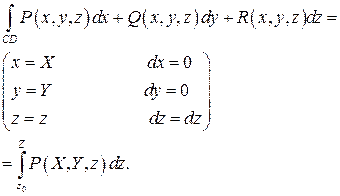
Отсюда  . Аналогично доказываются остальные равенства.
. Аналогично доказываются остальные равенства.
ЛЕКЦИЯ 12
Дифференциальные векторные операции 2-го порядка. Гармоническое поле, уравнение Лапласа, гармонические функции. Разложение произвольного векторного поля, уравнение Пуассона. Ортогональные криволинейные координаты. Выражение оператора Лапласа в ортогональных координатах
1. Дифференциальные векторные операции 2-го порядка
Рассмотрим скалярное поле  и векторное поле
и векторное поле  .
.
Дифференциальными операциями первого порядка называются операции
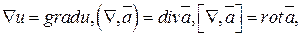
где  - оператор набла.
- оператор набла.
Дифференциальными операциями второго порядка называются попарные комбинации операций первого порядка. Рассмотрим эти операции
· 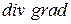 . Имеем
. Имеем

Выражение  называется оператором Лапласа.
называется оператором Лапласа.
·  . Имеем
. Имеем

·  . Имеем
. Имеем

·  . Имеем
. Имеем
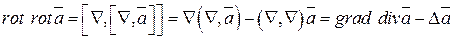 .
.
2. Гармоническое поле, уравнение Лапласа, гармонические функции
Векторное поле, которое одновременно является и соленоидальным и потенциальным, называется гармоническим.
Пусть поле  гармоническое
гармоническое 

Итак, потенциал гармонического поля удовлетворяет уравнению  - уравнению Лапласа
- уравнению Лапласа
 .
.
Решения уравнения Лапласа называются гармоническими функциями.
3. Разложение произвольного векторного поля, уравнение Пуассона
Теорема. Для любого векторного поля  справедливо разложение:
справедливо разложение:  , где
, где  - потенциальное поле,
- потенциальное поле,  - соленоидальное поле.
- соленоидальное поле.
Действительно, по определению потенциального поля  есть градиент некоторого скалярного поля u:
есть градиент некоторого скалярного поля u:  . Поэтому для вектора
. Поэтому для вектора  имеем
имеем
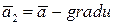 Чтобы векторное поле
Чтобы векторное поле  было соленоидальным, оно должно удовлетворять условию
было соленоидальным, оно должно удовлетворять условию  , откуда
, откуда 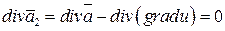 . Таким образом, для скалярного потенциала поля
. Таким образом, для скалярного потенциала поля  получаем уравнение
получаем уравнение
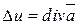 ,
,
называемое уравнением Пуассона:  .
.
4. Ортогональные криволинейные координаты. Выражение оператора Лапласа в ортогональных координатах
Дифференциальный оператор Лапласа второго порядка  для функции
для функции  переменных
переменных  задается равенством
задается равенством

Тогда
 - уравнение Лапласа.
- уравнение Лапласа.
Если  - ортогональные координаты, то оператор Лапласа в новых координат примет следующий вид:
- ортогональные координаты, то оператор Лапласа в новых координат примет следующий вид:

Оператор Лапласа в полярных координатах в  :
:
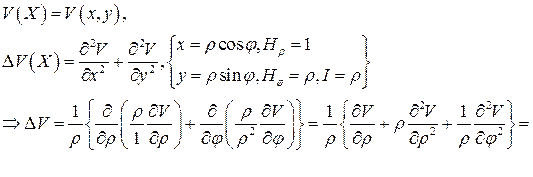
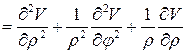 .
.
Оператор Лапласа в цилиндрических координатах:

Оператор Лапласа в сферических координатах:


ЛЕКЦИЯ 13


 некоторая двусторонняя поверхность,
некоторая двусторонняя поверхность,  - векторное поле на поверхности
- векторное поле на поверхности 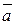 . Этот интеграл запишется следующим образом:
. Этот интеграл запишется следующим образом: .
. . Остальные интегралы будут определяться аналогично.
. Остальные интегралы будут определяться аналогично. . Стороны на этой поверхности можно выбирать следующим образом:
. Стороны на этой поверхности можно выбирать следующим образом: - это сторона поверхности, нормаль к которой образует с осью
- это сторона поверхности, нормаль к которой образует с осью  острый угол;
острый угол; - это сторона поверхности, нормаль к которой образует с осью
- это сторона поверхности, нормаль к которой образует с осью 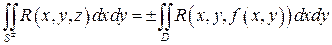 .
. .
.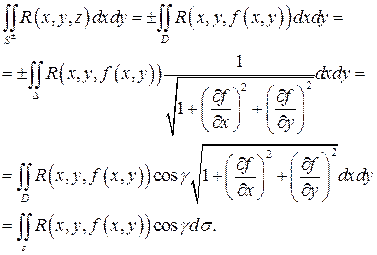
 .
. - тело, ограниченное этой поверхностью,
- тело, ограниченное этой поверхностью, 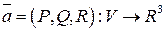 .
.
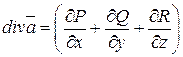 - дивергенция поля
- дивергенция поля  ,
, .
. ,
,  ,
, 
 . Тогда
. Тогда


 - пространственное тело, ограниченное кусочно-гладкой поверхностью
- пространственное тело, ограниченное кусочно-гладкой поверхностью  . На поверхности
. На поверхности  и
и  . В этих предположениях выполняется утверждение.
. В этих предположениях выполняется утверждение. ,
, - производная
- производная  по направлению внешней нормали
по направлению внешней нормали  .
. .
.
 . Пусть
. Пусть 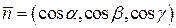 . Тогда поверхностные интегралы второго рода в правых частях могут быть записаны как поверхностные интегралы первого рода:
. Тогда поверхностные интегралы второго рода в правых частях могут быть записаны как поверхностные интегралы первого рода:
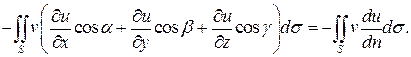

 в области
в области  называется соленоидальным, если для любого замкнутой поверхности
называется соленоидальным, если для любого замкнутой поверхности  поток через нее равен нулю. Из теоремы Гаусса – Остроградского вытекает следующее утверждение.
поток через нее равен нулю. Из теоремы Гаусса – Остроградского вытекает следующее утверждение. - соленоидальное в E;
- соленоидальное в E; в области E;
в области E; .
.

 - двусторонняя поверхность
- двусторонняя поверхность .
.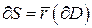 - граница (или край) поверхности S.
- граница (или край) поверхности S. согласованы, то
согласованы, то


 .
.









 называется потенциальным, если существует скалярное поле
называется потенциальным, если существует скалярное поле 

 вдоль замкнутой кривой L называется криволинейный интеграл второго рода
вдоль замкнутой кривой L называется криволинейный интеграл второго рода
 .
. любая циркуляция в E равна 0.
любая циркуляция в E равна 0. в области E;
в области E;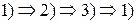 .
. :
: 


 .
. Имеем
Имеем

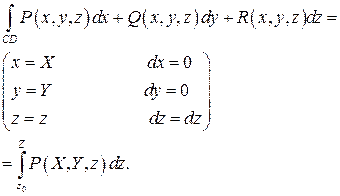
 . Аналогично доказываются остальные равенства.
. Аналогично доказываются остальные равенства.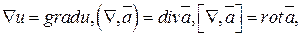
 - оператор набла.
- оператор набла. . Имеем
. Имеем
 называется оператором Лапласа.
называется оператором Лапласа. . Имеем
. Имеем
 . Имеем
. Имеем
 . Имеем
. Имеем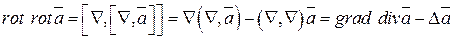 .
.

 - уравнению Лапласа
- уравнению Лапласа .
. , где
, где  - потенциальное поле,
- потенциальное поле,  - соленоидальное поле.
- соленоидальное поле. . Поэтому для вектора
. Поэтому для вектора 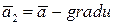 Чтобы векторное поле
Чтобы векторное поле  , откуда
, откуда 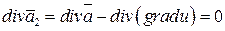 . Таким образом, для скалярного потенциала поля
. Таким образом, для скалярного потенциала поля 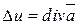 ,
, .
. для функции
для функции  переменных
переменных 
 - уравнение Лапласа.
- уравнение Лапласа. - ортогональные координаты, то оператор Лапласа в новых координат примет следующий вид:
- ортогональные координаты, то оператор Лапласа в новых координат примет следующий вид:
 :
: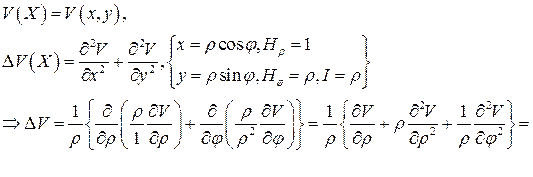
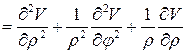 .
.