Иванов В.И.
профессор, д.ф.-м.н.
КОНСПЕКТ ЛЕКЦИЙ
по дисциплине
Математический анализ
(Часть 3)
Направление подготовки: 010400 «Прикладная математика и информатика»
Профиль подготовки: «Прикладная математика и информатика»
Форма обучения: очная
Тула 2013 г.
Рассмотрено на заседании кафедры
протокол № 1 от 02 сентября 2013 г.
Зав. кафедрой________________В.И. Иванов
СОДЕРЖАНИЕ
ЛЕКЦИЯ 1. Двойной интеграл по прямоугольной области. Два определения. Их эквивалентность. Критерий интегрируемости Римана. Вычисление интеграла путем сведения к повторному. 4
ЛЕКЦИЯ 2. Критерий Лебега существования двойного интеграла по прямоугольной области. 8
ЛЕКЦИЯ 3. Мера Жордана. Двойной интеграл по измеримой по Жордану области. Свойства двойного интеграла. Теорема о среднем. Вычисление двойного интеграла. 11
ЛЕКЦИЯ 4. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах 15
ЛЕКЦИЯ 5. Тройной интеграл, его вычисление. Замена переменных в тройном интеграле. Тройной интеграл в цилиндрических и сферических координатах. 17
ЛЕКЦИЯ 6. Механические приложения двойного и тройного интеграла. 20
ЛЕКЦИЯ 7. Криволинейный интеграл 1-го рода. Его свойства, вычисление, приложения. 21
ЛЕКЦИЯ 8. Криволинейный интеграл 2-го рода. Его физический смысл. Формула Грина. Условия независимости интеграла от пути в R 2. 25
ЛЕКЦИЯ 9. Площадь поверхности в R 3. Поверхностный интеграл 1-го рода. Его свойства, вычисление, приложения 29
ЛЕКЦИЯ 10. Поверхностный интеграл 2-го рода. Его связь с поверхностным интегралом 1-го рода. Соленоидальное поле. Дивергенция. Теорема Гаусса-Остроградского. Потенциальное поле. 32
ЛЕКЦИЯ 11. Циркуляция. Ротор. Формула Стокса. Поток векторного поля. Условия независимости криволинейного интеграла 2-го рода от пути в R 3 35
ЛЕКЦИЯ 12. Дифференциальные векторные операции 2-го порядка. Гармоническое поле, гармонические функции. Ортогональные криволинейные координаты. Коэффициенты Ламе. Выражение оператора Лапласа в ортогональных координатах. 39
ЛЕКЦИЯ 13. Сходимость и сумма числового ряда. Свойства сходящихся числовых рядов. Необходимые условия сходимости. Критерий Коши. 42
ЛЕКЦИЯ 14. Сходимость рядов с положительными членами. Критерий сходимости. Признак сравнения. Признак Даламбера. 44
ЛЕКЦИЯ 15. Радикальный признак Коши. Признак Коши для рядов с монотонными членами. Интегральный признак Коши. 47
ЛЕКЦИЯ 16. Ряды с произвольными членами. Абсолютная и условная сходимости. Признаки Лейбница, Абеля, Дирихле. 50
ЛЕКЦИЯ 17. Условная и безусловная сходимости. Теорема Римана о перестановках условно сходящегося ряда. Критерий безусловной сходимости. Сходимость бесконечного произведения. Необходимое условие сходимости. Сведение сходимости бесконечного произведения к сходимости числового ряда. Абсолютная и условная сходимости. 53
ЛЕКЦИЯ 1
Двойной интеграл по прямоугольной области. Два определения. Их эквивалентность. Критерий интегрируемости Римана. Вычисление интеграла путем сведения к повторному
1. Двойной интеграл по прямоугольной области. Два определения
Пусть 
 -параллелепипед в
-параллелепипед в 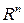 (замкнутый параллелепипед с гранями параллельными координатным плоскостям),
(замкнутый параллелепипед с гранями параллельными координатным плоскостям),  - объем параллелепипеда, функция
- объем параллелепипеда, функция  -ограниченная.
-ограниченная.
Необходимо определить число связанное с  , называемое интегралом от
, называемое интегралом от  по множеству
по множеству  :
:  .
.
Для простоты все построения будем вести для  . В этом случае
. В этом случае

 ,
,

 .
.
Пусть  - множество точек
- множество точек  ,
,
 - разбиения отрезков
- разбиения отрезков  ,
,
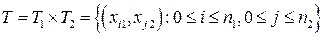 -разбиение прямоугольника
-разбиение прямоугольника  ; под разбиением
; под разбиением  прямоугольника
прямоугольника  будем понимать и маленькие прямоугольники
будем понимать и маленькие прямоугольники
 .
.
Этих прямоугольников будет 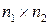 . Пусть далее
. Пусть далее
 - мелкость или диаметр разбиения
- мелкость или диаметр разбиения  (максимальная диагональ прямоугольников
(максимальная диагональ прямоугольников  ),
),
 - разметка разбиения
- разметка разбиения  ,
,
 размеченное разбиение.
размеченное разбиение.
В дальнейшем индексы у прямоугольников  будем опускать, т.е будем писать
будем опускать, т.е будем писать  .
.
Определим 3 типа интегральных сумм:
·  ,
, 
- интегральная сумма, отвечающая размеченному разбиению 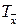 ;
;
·  - верхняя сумма Дарбу;
- верхняя сумма Дарбу;
·  -нижняя сумма Дарбу.
-нижняя сумма Дарбу.
Отметим следующие свойства этих сумм
1. Для любого  :
:  .
.
2. При измельчении разбиения  (получается путем добавления новых точек на
(получается путем добавления новых точек на  или
или  ) верхние суммы Дарбу не увеличиваются, а нижние суммы Дарбу не уменьшаются.
) верхние суммы Дарбу не увеличиваются, а нижние суммы Дарбу не уменьшаются.
3. Для любых 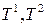 :
:  ,
,
Действительно, если  измельчение как
измельчение как 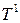 как и
как и  то
то  .
.
4. Если  - множество всех нижних сумм Дарбу,
- множество всех нижних сумм Дарбу, 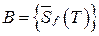 - множество всех верхних сумм Дарбу, то
- множество всех верхних сумм Дарбу, то  и по аксиоме непрерывности существует
и по аксиоме непрерывности существует  :
:  .
.
Определение 1.  - нижний интеграл Дарбу.
- нижний интеграл Дарбу.
Определение 2.  - верхний интеграл Дарбу.
- верхний интеграл Дарбу.
5. Для любых 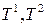 :
:  .
.
Определение 3. Первое определение интеграла Римана.
Будем говорить, что функция  интегрируема по Риману на прямоугольнике
интегрируема по Риману на прямоугольнике  и интеграл равен числу
и интеграл равен числу  , если существует
, если существует  , не зависящий от разметки
, не зависящий от разметки  , т.е для любого
, т.е для любого  существует
существует  такое, что для любого разбиения
такое, что для любого разбиения  и любой разметки
и любой разметки  разбиения
разбиения  :
:  .
.
Будем писать  .
.
Определение 4. Второе определение интеграла Римана.
Будем говорить, что функция  интегрируема по Риману на прямоугольнике
интегрируема по Риману на прямоугольнике  и интеграл равен числу
и интеграл равен числу  , если
, если  .
.
Критерий Коши. Для того чтобы функция  была интегрируема на прямоугольнике
была интегрируема на прямоугольнике  необходимо и достаточно,чтобы для любого
необходимо и достаточно,чтобы для любого  существовало
существовало  такое, что для любых разбиений
такое, что для любых разбиений  выполняется
выполняется
 .
.
2. Эквивалентность двух определений интеграла Римана
Доказательство эквивалентности двух определений интеграла Римана будет основано на двух леммах Дарбу.
Лемма 1.  .
.
Лемма 2.  .
.
Теорема. Оба определения интеграла Римана является эквивалентными, т.е
Если 
 в смысле первого определения, то
в смысле первого определения, то 
 в смысле определения второго и обратно.
в смысле определения второго и обратно.
Доказательство.
1.  . Доказательство опирается на вторую лемму Дарбу.
. Доказательство опирается на вторую лемму Дарбу.
Если 
 и не зависит от
и не зависит от  , то
, то  :
:  . Отсюда
. Отсюда 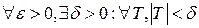 будет
будет
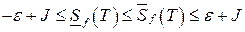 . Поэтому
. Поэтому

 ,
, 

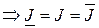 .
.
2. 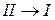 . Доказательство опирается на первую лемму Дарбу.
. Доказательство опирается на первую лемму Дарбу.
3. Критерий интегрируемости Римана
Теорема ( критерий интегрируемости Римана).
 , т.е
, т.е  интегрируема по Риману тогда и только тогда, когда
интегрируема по Риману тогда и только тогда, когда  .
.
Будем использовать запись  .
.
Здесь  - колебание функция на прямоугольнике
- колебание функция на прямоугольнике  (разность между самым большим и самым маленьким значением).
(разность между самым большим и самым маленьким значением).
Следствие.  является линейным пространством и кольцом.
является линейным пространством и кольцом.
Доказательство. Доказательство сводится к проверке замкнутости  относительно сложения и умножения.
относительно сложения и умножения.
Для доказательства оценим колебания на прямоугольнике суммы и произведение функций.
а.  .
.
Имеем 
 .
.
Далее  .
.
б. 
Имеем

Далее все очевидно.
Теорема.  , т.е. если функция
, т.е. если функция  непрерывна, то она интегрируема.
непрерывна, то она интегрируема.
Доказательство. Имеем  .
.
Если  , А- компактное, то
, А- компактное, то  равномерно непрерывна на А, поэтому
равномерно непрерывна на А, поэтому
 ,
, 
 такое, что
такое, что 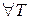 ,
,  и
и 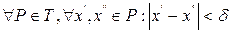 будет
будет  .
.
Итак  .
.
Отсюда, по критерию Римана  .
.
4. Вычисление интеграла путем сведения к повторному
Вычисление двойного интеграла по прямоугольнику основано на теореме Фубини. В этом случае она выглядит следующим образом.
Теорема Фубини. Если  , то для любого
, то для любого  ,
,  и справедливы следующие равенства
и справедливы следующие равенства

Последние два интеграла называют повторными.
ЛЕКЦИЯ 2
Доказательство.
Необходимость. Пусть функция  непрерывна в точке
непрерывна в точке  . Предположим, что
. Предположим, что 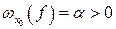 . Рассмотрим
. Рассмотрим  . Из определения
. Из определения  получим, что существуют точки
получим, что существуют точки  такие, что
такие, что  .
.
Кроме того, имеем  . Это противоречит непрерывности функции
. Это противоречит непрерывности функции  в точке
в точке  . Следовательно
. Следовательно  .
.
Достаточность. Поскольку  , то для любого
, то для любого  существует
существует  такое, что для любых
такое, что для любых  имеем
имеем  . Полагая
. Полагая  , получаем непрерывность в точке
, получаем непрерывность в точке  то лемма.
то лемма.
Лемма 4.  множество
множество  - ограниченное и замкнутое, т.е. компактное.
- ограниченное и замкнутое, т.е. компактное.
Доказательство. Так как  , то
, то  - ограниченное.
- ограниченное.
Пусть 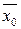 - предельная точка
- предельная точка  . Покажем, что она принадлежит
. Покажем, что она принадлежит  . Поскольку
. Поскольку 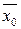 предельная точка, то существует последовательность
предельная точка, то существует последовательность  , сходящая к
, сходящая к 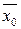 . Отсюда для любого
. Отсюда для любого  найдется
найдется 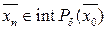 ,
,  открытое, поэтому существует
открытое, поэтому существует  такое, что
такое, что  . Отсюда имеем
. Отсюда имеем  , то есть
, то есть
 .
.
Лемма доказана.
Пусть 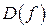 - множество точек разрыва функции
- множество точек разрыва функции  на прямоугольнике А.
на прямоугольнике А.
Лемма 5.  .
.
Множество, которое можно представить в виде счетного объединения замкнутых множеств называется множеством типа  . Итак, множество точек разрыва функции
. Итак, множество точек разрыва функции  - множество типа
- множество типа  .
.
3. Критерий Лебега
Теорема 1. ( Критерий Лебега).Ограниченная функия  тогда и только тогда, когда
тогда и только тогда, когда  .
.
Следствие. Всякая функция, имеющая не более чем счетное множество точек разрыва интегрируемая.
Теорема 2. ( Критерий интегрируемости). Ограниченная функия  тогда и только тогда, когда для любого
тогда и только тогда, когда для любого  .
.  .
.
Сначала  выведем теорему 1 из теоремы 2. Доказательство теоремы 1.
выведем теорему 1 из теоремы 2. Доказательство теоремы 1.
Необходимость. Ограниченная функция  по теореме 2, если для любого
по теореме 2, если для любого  .
.  .
.
Достаточность. 
По теореме 2 имеем  .
.
Теорема доказана.
Доказательство теоремы 2.
Необходимость. Предположим, что существует  ,
,  . То есть найдется
. То есть найдется  такое, что для любого набора
такое, что для любого набора  ,
,  , но
, но  . Рассмотрим любое разбиение Т прямоугольника А на прямоугольники
. Рассмотрим любое разбиение Т прямоугольника А на прямоугольники  . Пусть
. Пусть  -множество всех тех прямоугольников
-множество всех тех прямоугольников  , внутри которых находится хотя бы одна точка множества
, внутри которых находится хотя бы одна точка множества 
 . Заметим что для любого прямоугольника из
. Заметим что для любого прямоугольника из  колебание функции на этом прямоугольнике не меньше чем
колебание функции на этом прямоугольнике не меньше чем  . Отсюда для любого Т
. Отсюда для любого Т  Это означает, что функция не интегрируема на прямоугольнике. Получили противоречие. Значит, для любого
Это означает, что функция не интегрируема на прямоугольнике. Получили противоречие. Значит, для любого 
 .
.
Достаточность. Положим  .
.
Так как  , то его можно покрыть открытыми прямоугольниками
, то его можно покрыть открытыми прямоугольниками  ,
,  . Выделим из
. Выделим из  конечное подпокрытие
конечное подпокрытие  . Рассмотрим
. Рассмотрим  . Оно является компактом. Для любого
. Оно является компактом. Для любого  ,
,  .Из определения
.Из определения  получим, что существует открытый квадрат Н такой, что колебание функции на нем меньше чем
получим, что существует открытый квадрат Н такой, что колебание функции на нем меньше чем  . Квадраты Н образуют открытое покрытие множества К. Выделим из него конечное покрытие V. Продолжим стороны прямоугольников, составляющих I и V до пересечения со сторонами прямоугольника А. Получим разбиение Т, для которого
. Квадраты Н образуют открытое покрытие множества К. Выделим из него конечное покрытие V. Продолжим стороны прямоугольников, составляющих I и V до пересечения со сторонами прямоугольника А. Получим разбиение Т, для которого
 .
.
Таким образом,  .
.
Теорема доказана.
Следствия из критерия Лебега.
1.  .
.
2.  .
.
3. Пусть  . Тогда
. Тогда  .
.
ЛЕКЦИЯ 3
ЛЕКЦИЯ 4
ЛЕКЦИЯ 5
ЛЕКЦИЯ 6
ЛЕКЦИЯ 7
ЛЕКЦИЯ 8
Криволинейный интеграл 2-го рода. Его физический смысл. Формула Грина. Условия независимости интеграла от пути в R2
1. Криволинейный интеграл 2-го рода. Его физический смысл
Пусть  - гладкая кривая,
- гладкая кривая,
 .
.
Пусть  - разбиение отрезка
- разбиение отрезка  ,
,
 - мелкость разбиения,
- мелкость разбиения,
 -
-  разметка разбиения.
разметка разбиения.
Образуем следующую интегральную сумму:
 Будем говорить, что для функций
Будем говорить, что для функций  существует криволинейный интеграл второго рода по кривой
существует криволинейный интеграл второго рода по кривой  в направлении возрастания параметра
в направлении возрастания параметра  (от начальной точки кривой к конечной точке), если существует
(от начальной точки кривой к конечной точке), если существует  , не зависящий от
, не зависящий от  , т.е.
, т.е.

Этой интеграл имеет следующее обозначение
 .
.
Он зависит от ориентации кривой

В случае замкнутой кривой различают положительную и отрицательную ориентацию: против часовой стрелки и по часовой стрелке.
Этот случай подчеркивают следующим обозначением
 .
.
Функции  в записи интеграла можно считать координатами вектора
в записи интеграла можно считать координатами вектора  . Его называют векторным полем, заданным на кривой
. Его называют векторным полем, заданным на кривой  .
.
Обозначим 
Криволинейный интеграл  определяет работу векторного (силового) поля
определяет работу векторного (силового) поля 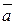 вдоль кривой
вдоль кривой  в направление от точки А к точке В. Работу по замкнутой кривой часто называют циркуляцией.
в направление от точки А к точке В. Работу по замкнутой кривой часто называют циркуляцией.
2. Формула Грина
Теорема (Формула Грина). Пусть в односвязной области  задано векторное поле
задано векторное поле  таким, что функции
таким, что функции  - непрерывные в Е.Кривая
- непрерывные в Е.Кривая  , множество
, множество  , ограниченное этой кривой выпуклое. Тогда справедлива формула
, ограниченное этой кривой выпуклое. Тогда справедлива формула
 .
.
Здесь кривая  обходится в положительном направлении.
обходится в положительном направлении.
Доказательство. Будем считать, что рассматриваемая область односвязная, т.е. в ней нет исключенных участков.
 y
y
y = y2(x)
D
A
C
B
y= y1(x)
0 x1 x2 x
Если замкнутый контур имеет вид, показанный на рисунке, то криволинейный интеграл по контуру L можно записать в виде:


Рассуждая аналогично, для области правильной при проектировании на ось 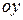 , получим
, получим
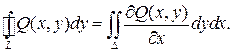 (2)
(2)
Складывая (1) и (2), получим формулу Грина.
3. Условия независимости интеграла от пути в R 2
Лемма. Работа векторного поля не зависит от пути тогда и только тогда, когда любая циркуляция равна 0.
Доказательство. Пусть  произвольный замкнутый контур, точки А и В – любые точки на
произвольный замкнутый контур, точки А и В – любые точки на  . Тогда
. Тогда
 .
.
Работа векторного поля не зависит от пути  .
.
Лемма доказана.
Векторное поле  называется потенциальным, если существует функция 2-х переменных
называется потенциальным, если существует функция 2-х переменных  - скалярное поле такое, что
- скалярное поле такое, что  ,т.е
,т.е  .
.
Замечание. В дифференциальных уравнениях уравнение первого порядка, записанное в дифференциалах  называется уравнением в полных дифференциалах, если существует скалярное поле
называется уравнением в полных дифференциалах, если существует скалярное поле  :
:  .
.
В этом случае общий интеграл уравнения имеет вид 
Теорема. Если в односвязной области  функции
функции 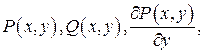
 непрерывны, то следующие условия эквивалентны:
непрерывны, то следующие условия эквивалентны:
1) поле  - потенциальное в
- потенциальное в  ;
;
2)  в
в  ;
;
3) Работа поля  в
в  не зависит от пути.
не зависит от пути.
Доказательство. Будем следовать схеме  .
.
· 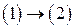
Поле  - потенциальное в
- потенциальное в  , поэтому
, поэтому 
 -скалярное поле:
-скалярное поле:  , т.е.
, т.е. 
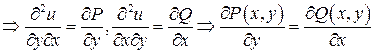 .
.
· 
Достаточно проверить, что любая циркуляция в  равна 0.
равна 0.
Используем формулу Грина, получим
 .
.
· 
Покажем, что следующее скалярное поле и есть искомый потенциал:

Итак,



 -потенциальное поле в
-потенциальное поле в  .
.
ЛЕКЦИЯ 9
Площадь поверхности в R3. Поверхностный интеграл 1-го рода. Его свойства, вычисление, приложения
1. Площадь поверхности в R 3
Поверхность в  задается параметрически при помощи 2 параметров
задается параметрически при помощи 2 параметров

 ,
,
 ,
,
 - поверхность в
- поверхность в  .
.
Иногда поверхность задают при помощи одной функции двух переменных
 .
.
Поверхность  называется гладкой если:
называется гладкой если:
 .
.
Из этих частных производных можно записать матрицу Якоби нашего отображения
 .
.
Точку  назовем не особой, если ранг А в этой точке максимален и равен двум. В не особой точке векторы-столбцы являются линейно не зависимыми.
назовем не особой, если ранг А в этой точке максимален и равен двум. В не особой точке векторы-столбцы являются линейно не зависимыми.
Выясним геометрический смысл этих векторов. Эти векторы  - касательные векторы к линиям
- касательные векторы к линиям  на поверхности. В не особой точке эти касательные векторы не коллинеарные.
на поверхности. В не особой точке эти касательные векторы не коллинеарные.
Можно показать, что все касательные векторы к кривым на поверхности, проходящие через  , лежат в одной плоскости. Эта плоскость называется касательной плоскостью к поверхности в точке
, лежат в одной плоскости. Эта плоскость называется касательной плоскостью к поверхности в точке 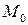 .
.
В не особой точке уравнение касательной плоскости можно записать с помощью точки  и двух касательных векторов
и двух касательных векторов  :
:
 .
.
Рассмотрим вектор  .
.
Очень часто в качестве нормального вектора будем использовать единичный нормальный вектор

Определим первую квадратную форму на поверхности. Пусть



Таким образом, п ервая квадратичная форма на поверхности имеет вид:
 .
.
Определение. Площадью гладкой поверхности  ,
,  -измеримо по Жордану, называется число:
-измеримо по Жордану, называется число:  .
.
Преобразуем эту формулу для площади поверхности
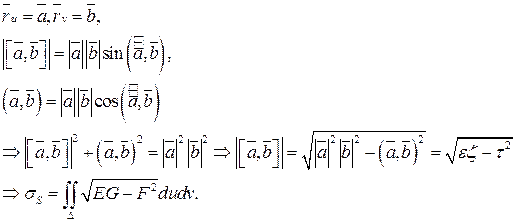
2. Поверхностный интеграл 1-го рода. Его свойства, вычисление
Пусть поверхность  ,
, 
 - непрерывная функция.
- непрерывная функция.
Определение. Поверхностным интегралом первого рода по поверхности  от функции
от функции  называется число
называется число
 .
.
Здесь  - элемент площади поверхности.
- элемент площади поверхности.
Данное определение справедливо и для кусочно-гладкой поверхности, т.е. поверхности, которая может быть разбита на конечное число гладких участков.
Поверхностный интеграл первого рода сводится к некоторому двойному интегралу и для него справедливы все его свойства.
3. Приложения поверхностного интеграла 1-го рода
Геометрическое приложение: Вычисление площади поверхности 
Механические приложения: Вычисление массы, статических моментов, координат центра тяжести поверхности, начиненной веществом с плотностью  .
.
Масса:  .
.
Первые статические моменты относительно координатных плоскостей:

Координаты центра тяжести:
 .
.
Вторые статические моменты относительно координатных плоскостей:
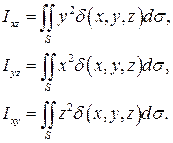
Статический момент (момент инерции) относительно начала координат:
 .
.
ЛЕКЦИЯ 10
ЛЕКЦИЯ 11
Формула Стокса. Условия независимости криволинейного интеграла 2-го рода от пути в R3. Потенциальное поле. Циркуляция. Ротор
1. Формула Стокса
Пусть 

 - двусторонняя поверхность
- двусторонняя поверхность
 .
.
Тогда множество 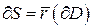 - граница (или край) поверхности S.
- граница (или край) поверхности S.
Теорема (Формула Стокса ). Если ориентации на  и
и  согласованы, то
согласованы, то

Доказательство. Необходимо доказать равенство

или три равенства

Для простоты докажем первое равенство в предложении, что поверхность
 .
.
Имеем










Что и требовать показать.
3. Потенциальное поле. Циркуляция. Ротор
Векторное поле  называется потенциальным, если существует скалярное поле
называется потенциальным, если существует скалярное поле  - потенциал такой, что
- потенциал такой, что 
т.е.  есть решение системы
есть решение системы 
Циркуляцией векторного поля  вдоль замкнутой кривой L называется криволинейный интеграл второго рода
вдоль замкнутой кривой L называется криволинейный интеграл второго рода

В случае, когда векторное поле  является силовым полем, циркуляция даёт величину работы этого поля вдоль кривой L.
является силовым полем, циркуляция даёт величину работы этого поля вдоль кривой L.
Ротором (или вихрем) дифференцируемого векторного поля  называется вектор
называется вектор
 .
.
2. Условия независимости криволинейного интеграла 2-го рода от пути в R 3
Лемма. Работа векторного поля  в области
в области  не зависит от пути, а зависит только от начала и конца пути
не зависит от пути, а зависит только от начала и конца пути  любая циркуляция в E равна 0.
любая циркуляция в E равна 0.
Доказательство. Точно такое же, как в плоском случае.
Теорема. Следующие условия эквивалентны:
1) поле  потенциальное, в односвязной области E;
потенциальное, в односвязной области E;
2) ротор  в области E;
в области E;
3) работа поля  в E не зависит от пути.
в E не зависит от пути.
Доказательство. Будем следовать схеме 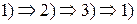 .
.
 :
: 


|
|
|




 -параллелепипед в
-параллелепипед в 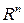 (замкнутый параллелепипед с гранями параллельными координатным плоскостям),
(замкнутый параллелепипед с гранями параллельными координатным плоскостям),  - объем параллелепипеда, функция
- объем параллелепипеда, функция  -ограниченная.
-ограниченная. , называемое интегралом от
, называемое интегралом от  по множеству
по множеству  :
:  .
. . В этом случае
. В этом случае
 ,
,
 .
. - множество точек
- множество точек  ,
, - разбиения отрезков
- разбиения отрезков  ,
,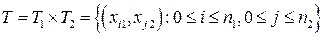 -разбиение прямоугольника
-разбиение прямоугольника  ; под разбиением
; под разбиением  прямоугольника
прямоугольника  .
.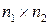 . Пусть далее
. Пусть далее - мелкость или диаметр разбиения
- мелкость или диаметр разбиения  ),
), - разметка разбиения
- разметка разбиения  размеченное разбиение.
размеченное разбиение. .
. ,
, 
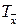 ;
; - верхняя сумма Дарбу;
- верхняя сумма Дарбу; -нижняя сумма Дарбу.
-нижняя сумма Дарбу. :
:  .
. или
или  ) верхние суммы Дарбу не увеличиваются, а нижние суммы Дарбу не уменьшаются.
) верхние суммы Дарбу не увеличиваются, а нижние суммы Дарбу не уменьшаются.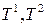 :
:  ,
,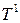 как и
как и  то
то  .
. - множество всех нижних сумм Дарбу,
- множество всех нижних сумм Дарбу, 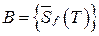 - множество всех верхних сумм Дарбу, то
- множество всех верхних сумм Дарбу, то  и по аксиоме непрерывности существует
и по аксиоме непрерывности существует  :
:  .
. - нижний интеграл Дарбу.
- нижний интеграл Дарбу. - верхний интеграл Дарбу.
- верхний интеграл Дарбу. .
. , если существует
, если существует  , не зависящий от разметки
, не зависящий от разметки  существует
существует  такое, что для любого разбиения
такое, что для любого разбиения  и любой разметки
и любой разметки  .
. .
. .
. выполняется
выполняется .
. .
. .
.
 в смысле первого определения, то
в смысле первого определения, то  . Доказательство опирается на вторую лемму Дарбу.
. Доказательство опирается на вторую лемму Дарбу. :
:  . Отсюда
. Отсюда 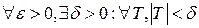 будет
будет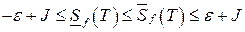 . Поэтому
. Поэтому ,
, 
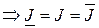 .
.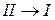 . Доказательство опирается на первую лемму Дарбу.
. Доказательство опирается на первую лемму Дарбу. , т.е
, т.е  .
. .
. - колебание функция на прямоугольнике
- колебание функция на прямоугольнике  (разность между самым большим и самым маленьким значением).
(разность между самым большим и самым маленьким значением). является линейным пространством и кольцом.
является линейным пространством и кольцом. .
.
 .
. .
.

 , т.е. если функция
, т.е. если функция  .
. , А- компактное, то
, А- компактное, то  ,
, 
 такое, что
такое, что 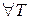 ,
,  и
и 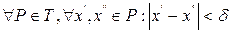 будет
будет  .
. .
. , то для любого
, то для любого  ,
,  и справедливы следующие равенства
и справедливы следующие равенства
 . Предположим, что
. Предположим, что 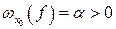 . Рассмотрим
. Рассмотрим  . Из определения
. Из определения  получим, что существуют точки
получим, что существуют точки  такие, что
такие, что  .
. . Это противоречит непрерывности функции
. Это противоречит непрерывности функции  .
. имеем
имеем  . Полагая
. Полагая  , получаем непрерывность в точке
, получаем непрерывность в точке  множество
множество  - ограниченное и замкнутое, т.е. компактное.
- ограниченное и замкнутое, т.е. компактное. , то
, то  - ограниченное.
- ограниченное.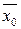 - предельная точка
- предельная точка  , сходящая к
, сходящая к 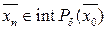 ,
,  открытое, поэтому существует
открытое, поэтому существует  такое, что
такое, что  . Отсюда имеем
. Отсюда имеем  , то есть
, то есть .
.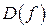 - множество точек разрыва функции
- множество точек разрыва функции  .
. . Итак, множество точек разрыва функции
. Итак, множество точек разрыва функции  .
. .
.  .
. .
.  .
.
 . То есть найдется
. То есть найдется  ,
,  , но
, но  . Рассмотрим любое разбиение Т прямоугольника А на прямоугольники
. Рассмотрим любое разбиение Т прямоугольника А на прямоугольники  -множество всех тех прямоугольников
-множество всех тех прямоугольников  . Заметим что для любого прямоугольника из
. Заметим что для любого прямоугольника из  . Отсюда для любого Т
. Отсюда для любого Т  Это означает, что функция не интегрируема на прямоугольнике. Получили противоречие. Значит, для любого
Это означает, что функция не интегрируема на прямоугольнике. Получили противоречие. Значит, для любого  .
. .
. . Выделим из
. Выделим из  . Рассмотрим
. Рассмотрим  . Оно является компактом. Для любого
. Оно является компактом. Для любого  ,
,  .Из определения
.Из определения  получим, что существует открытый квадрат Н такой, что колебание функции на нем меньше чем
получим, что существует открытый квадрат Н такой, что колебание функции на нем меньше чем  . Квадраты Н образуют открытое покрытие множества К. Выделим из него конечное покрытие V. Продолжим стороны прямоугольников, составляющих I и V до пересечения со сторонами прямоугольника А. Получим разбиение Т, для которого
. Квадраты Н образуют открытое покрытие множества К. Выделим из него конечное покрытие V. Продолжим стороны прямоугольников, составляющих I и V до пересечения со сторонами прямоугольника А. Получим разбиение Т, для которого .
. .
. .
. . Тогда
. Тогда  .
. - гладкая кривая,
- гладкая кривая, .
. - разбиение отрезка
- разбиение отрезка  ,
, - мелкость разбиения,
- мелкость разбиения, -
-  разметка разбиения.
разметка разбиения. Будем говорить, что для функций
Будем говорить, что для функций  существует криволинейный интеграл второго рода по кривой
существует криволинейный интеграл второго рода по кривой  в направлении возрастания параметра
в направлении возрастания параметра  (от начальной точки кривой к конечной точке), если существует
(от начальной точки кривой к конечной точке), если существует  , не зависящий от
, не зависящий от  , т.е.
, т.е.
 .
.
 .
. . Его называют векторным полем, заданным на кривой
. Его называют векторным полем, заданным на кривой  .
.
 определяет работу векторного (силового) поля
определяет работу векторного (силового) поля 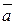 вдоль кривой
вдоль кривой  в направление от точки А к точке В. Работу по замкнутой кривой часто называют циркуляцией.
в направление от точки А к точке В. Работу по замкнутой кривой часто называют циркуляцией. задано векторное поле
задано векторное поле  - непрерывные в Е.Кривая
- непрерывные в Е.Кривая  , множество
, множество  , ограниченное этой кривой выпуклое. Тогда справедлива формула
, ограниченное этой кривой выпуклое. Тогда справедлива формула .
. y
y

 , получим
, получим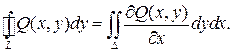 (2)
(2) .
. .
. - скалярное поле такое, что
- скалярное поле такое, что  ,т.е
,т.е  .
. называется уравнением в полных дифференциалах, если существует скалярное поле
называется уравнением в полных дифференциалах, если существует скалярное поле  .
.
 функции
функции 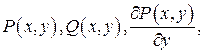
 непрерывны, то следующие условия эквивалентны:
непрерывны, то следующие условия эквивалентны: в
в  .
.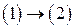
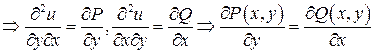 .
.
 .
.




 задается параметрически при помощи 2 параметров
задается параметрически при помощи 2 параметров
 ,
, ,
, - поверхность в
- поверхность в  .
. называется гладкой если:
называется гладкой если: .
. .
. назовем не особой, если ранг А в этой точке максимален и равен двум. В не особой точке векторы-столбцы являются линейно не зависимыми.
назовем не особой, если ранг А в этой точке максимален и равен двум. В не особой точке векторы-столбцы являются линейно не зависимыми. - касательные векторы к линиям
- касательные векторы к линиям  на поверхности. В не особой точке эти касательные векторы не коллинеарные.
на поверхности. В не особой точке эти касательные векторы не коллинеарные. , лежат в одной плоскости. Эта плоскость называется касательной плоскостью к поверхности в точке
, лежат в одной плоскости. Эта плоскость называется касательной плоскостью к поверхности в точке  :
: .
. .
.



 .
. ,
,  -измеримо по Жордану, называется число:
-измеримо по Жордану, называется число:  .
.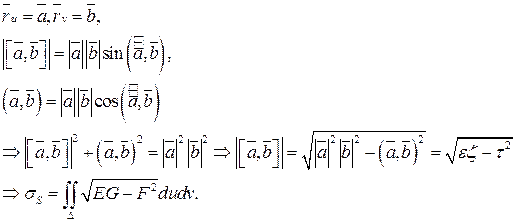
 ,
, 
 - непрерывная функция.
- непрерывная функция. от функции
от функции  называется число
называется число .
. - элемент площади поверхности.
- элемент площади поверхности.
 .
. .
.
 .
.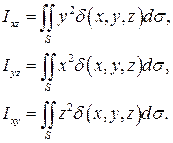
 .
.

 - двусторонняя поверхность
- двусторонняя поверхность .
. - граница (или край) поверхности S.
- граница (или край) поверхности S. согласованы, то
согласованы, то


 .
.









 называется потенциальным, если существует скалярное поле
называется потенциальным, если существует скалярное поле  - потенциал такой, что
- потенциал такой, что 
 есть решение системы
есть решение системы 
 вдоль замкнутой кривой L называется криволинейный интеграл второго рода
вдоль замкнутой кривой L называется криволинейный интеграл второго рода
 .
. в области
в области  не зависит от пути, а зависит только от начала и конца пути
не зависит от пути, а зависит только от начала и конца пути  любая циркуляция в E равна 0.
любая циркуляция в E равна 0. потенциальное, в односвязной области E;
потенциальное, в односвязной области E; в области E;
в области E;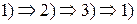 .
. :
: 





