Не всякое плоское движение является равноускоренным. Пример плоского неравноускоренного движения, известный вам из школьного курса физики, — это равномерное движение по окружности. Давайте рассмотрим его здесь. Поскольку это движение плоское, выберем в качестве этой плоскости, плоскость ХУ. Начало координат выберем в центре окружности.
Координаты частицы выразим через величину радиуса окружности r и угол φ: x=r cosφ,
y=r sinφ.
Поскольку движение происходит по окружности, r от времени не зависит. Функцией времени является только угол φ (t). Производная от угла по времени называется угловой скоростью вращения w:
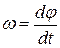 . (3.1)
. (3.1)
При равномерном вращении по окружности w=const и можно проинтегрировать это уравнение, результате
φ =wt+const. (3.2)
Константа интегрирования выбирается из условия φ (0) = 0. Таким образом,
x=r coswt,
y=r sinwt.
Это полностью определяет движение.
Для характеристики изменения угловой скорости вводится понятие – угловое ускорение.
Средним угловым ускорением называется вектор < 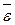 >, равный отношению вектора Δ
>, равный отношению вектора Δ  =
=  2 –
2 –  1 к промежутку времени Δ t, в течение которого произошло изменение угловой скорости:
1 к промежутку времени Δ t, в течение которого произошло изменение угловой скорости:
< 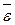 > =
> = 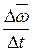 .
.
Переходя к пределу для бесконечно малого промежутка времени, получим вектор мгновенного углового ускорения тела в момент времени t:
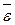 =
= 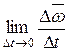 =
=  (3.3)
(3.3)
или с учетом, что угловая скорость есть первая производная угловой координаты от времени
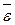 =
= 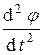 . (3.4)
. (3.4)
Очевидно, что вектора < 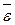 > и
> и 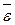 совпадают по направлению с вектором изменения угловой скорости Δ
совпадают по направлению с вектором изменения угловой скорости Δ  .
.
При рассмотрении вращательного движения мы ввели угловую скорость вращения w как производную по времени от угла поворота. Давайте теперь зададимся вопросом, какой величиной, скалярной или векторной, является угол поворота. Ведь когда говорят о повороте, нужно указывать не только величину угла поворота, но и то, вокруг какой оси происходит вращение (поворот) и в какую сторону (по часовой стрелке или против). С этой точки зрения угол поворота должен быть величиной векторной. Поэтому, говоря о повороте на какой-то малый угол D φ, можно приближенно говорить о векторе D φ, величина которого равна углу поворота, а направление показывает направление оси вращения так, чтобы поворот происходил по часовой стрелке, или в соответствии с правилом буравчика.
Если речь идет о бесконечно малых поворотах dφ, тогда бесконечно малым является и перемещение dr. Его величина (равная длине хорды) совпадает теперь с длиной дуги, то есть \dr\=rdφ, а по направлению вектор dr совпадает с касательной, то есть перпендикулярен r. В результате мы имеем три взаимно перпендикулярные вектора r, dr и dφ, образующие правую тройку, причем |dr| = dφ r. Те, кто помнят из школьного курса о векторном произведении векторов, без труда сообразят, что искомое соотношение можно записать в виде векторного произведения:
dr =[d φ ´ r ]. (3.5)
Разделив обе стороны этого равенства на бесконечно малый временной интервал dt, в течение которого произошло изменение вектора r на dr, мы получим  .
.
 Но величина, стоящая в левой части равенства, есть не что иное, как скорость частицы υ, а производная
Но величина, стоящая в левой части равенства, есть не что иное, как скорость частицы υ, а производная  = w называется вектором угловой скорости. Ее мы вначале ввели по абсолютной величине, а теперь показали, что имеет смысл говорить об угловой скорости вращения как о векторе. Ее величина определяет величину угловой скорости (скорость вращения, или скорость изменения угла), а направление параллельно оси вращения, причем так, что имеет место правило буравчика. Итак, мы получили, что υ = [w ´ r]. Ориентация этих трех векторов показана на рис. 3.2.
= w называется вектором угловой скорости. Ее мы вначале ввели по абсолютной величине, а теперь показали, что имеет смысл говорить об угловой скорости вращения как о векторе. Ее величина определяет величину угловой скорости (скорость вращения, или скорость изменения угла), а направление параллельно оси вращения, причем так, что имеет место правило буравчика. Итак, мы получили, что υ = [w ´ r]. Ориентация этих трех векторов показана на рис. 3.2.
Чтобы получить ускорение а, надо от обеих частей взять производную по времени. Если wпостоянно (как по величине, так и по направлению), то ускорение оказывается перпендикулярным угловой скорости вращения w и скорости движения υ. А поскольку последняя направлена по касательной, то, значит, ускорение направлено либо параллельно r, либо антипараллельно.
Поскольку вектор ускорения не совпадает по направлению с вектором скорости, то удобней ускорение разложить на две компоненты:
 в направлении скорости –
в направлении скорости –  t (тангенциальное ускорение); в перпендикулярном направлении –
t (тангенциальное ускорение); в перпендикулярном направлении –  n (нормальное ускорение), т.е.
n (нормальное ускорение), т.е.
 =
=  t +
t +  n
n
или
а =  (3.6)
(3.6)
Тангенциальное ускорение  t характеризует быстроту изменения численного значения скорости движения, нормальное ускорение
t характеризует быстроту изменения численного значения скорости движения, нормальное ускорение  n характеризует быстроту изменения направления скорости, тогда
n характеризует быстроту изменения направления скорости, тогда
 =
=  , а t =
, а t =  , а n =
, а n = 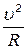 .
.
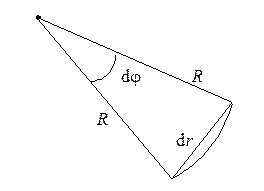 Поскольку вращательное движение может быть описано не только в угловых переменных, но и в линейных, установим между ними связь.
Поскольку вращательное движение может быть описано не только в угловых переменных, но и в линейных, установим между ними связь.
Из рис. видно, что d r = R sin d φ = R d φ (если угол выражен в радианах). По определению  , тогда
, тогда
υ = ω R. (3.7)
Нормальное ускорение а n = 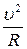 , тогда
, тогда
а n = ω 2 R. (3.8)
Тангенциальное ускорение
а t =  =
= 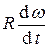 ,
,
тогда
а t = ε R. (3.9)
Полное мгновенное линейное ускорение а = 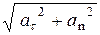 , тогда
, тогда
а =  . (3.10)
. (3.10)
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
Лекция 4
Инерциальные и неинерциальные системы отсчета. Движение относительно инерциальных систем отсчета. Законы Ньютона. Принцип относительности Галилея. Преобразование Галилея и Лоренца.
Динамика – раздел механики, изучающий движение материальных тел в пространстве и времени совместно с причинами, вызывающими это движение.
В основе динамики лежат законы И.Ньютона, сформулированные им в 1687 г. на основе экспериментальных данных и теоретических сведений, полученных Ньютоном и другими учеными.
При поступательном движении мерой механического воздействия на тела является сила 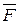 . Это векторная величина. Сила представляет собой обобщенную замену реальных взаимодействий между телами.
. Это векторная величина. Сила представляет собой обобщенную замену реальных взаимодействий между телами.
Мерой инертности тела при поступательном движении является масса m тела.
После введения понятий сила и масса, законы Ньютона можно сформулировать так:
Первый закон Ньютона. Если на тело (материальную точку) не действуют ни какие силы или все действующие силы скомпенсированы, то тело будет находиться в состоянии покоя или равномерного, прямолинейного движения.
а = 0, когда F = 0. (4.1)
Второй закон Ньютона. Если силы, действующие на тело, не скомпенсированы, то тело будет двигаться с ускорением 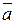 , величина которого пропорциональна результирующей силе
, величина которого пропорциональна результирующей силе 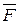 и обратно пропорционально массе тела m:
и обратно пропорционально массе тела m:
 .(4.2)
.(4.2)
Третий закон Ньютона. Тела взаимодействуют друг с другом силами равными по величине и противоположными по направлению.
F12 = -F21, (4.3)
Первые два закона движения выполняются только тогда, когда наблюдение ведется в системах отсчета, движущихся без ускорения. Такие системы отсчета называются инерциальными. Например, если тело в одной системе отсчета движется с постоянной скоростью и имеется система отсчета, которая движется с ускорением относительно нее то, очевидно, что тело будет двигаться относительно этой системы отсчета с ускорением.
Примером может служить система отсчета, неподвижно связанная с самолетом, который быстро набирает скорость при взлете. Благодаря ускорению, вас прижимает назад, к сидению, а сила, действующая со стороны спинки сидения, удерживает вас в состоянии покоя относительно этой системы.
Если бы вы находились в состоянии равномерного движения или покоя относительно системы отсчета, не имеющей ускорения, то для этого не требовалось бы никакой силы. Но если вы хотите находиться в состоянии покоя относительно системы отсчета, движущейся с ускорением, то вы должны прилагать силу или испытывать действие силы со стороны другого тела. Движение (его характер) в системах отсчета, движущихся с ускорением, играет важную роль в физике. Такие системы отсчета называются неинерциальными. Особенно важно понять характер движения тел во вращающейся системе отсчета (практическое применение — центрифуга), хотя бы потому, что мы с вами находимся как раз в такой системе отсчета (на Земле). Если существует хотя бы одна инерциальная система, то таких систем должно быть бесконечное множество, так как любая система, движущаяся с постоянной скоростью относительно инерциальной, тоже является инерциальной. Существует фундаментальный физический принцип, который называется принципом относительности Галилея.



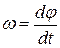 . (3.1)
. (3.1)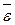 >, равный отношению вектора Δ
>, равный отношению вектора Δ  =
= 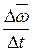 .
.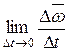 =
=  (3.3)
(3.3)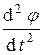 . (3.4)
. (3.4) .
. Но величина, стоящая в левой части равенства, есть не что иное, как скорость частицы υ, а производная
Но величина, стоящая в левой части равенства, есть не что иное, как скорость частицы υ, а производная  = w называется вектором угловой скорости. Ее мы вначале ввели по абсолютной величине, а теперь показали, что имеет смысл говорить об угловой скорости вращения как о векторе. Ее величина определяет величину угловой скорости (скорость вращения, или скорость изменения угла), а направление параллельно оси вращения, причем так, что имеет место правило буравчика. Итак, мы получили, что υ = [w ´ r]. Ориентация этих трех векторов показана на рис. 3.2.
= w называется вектором угловой скорости. Ее мы вначале ввели по абсолютной величине, а теперь показали, что имеет смысл говорить об угловой скорости вращения как о векторе. Ее величина определяет величину угловой скорости (скорость вращения, или скорость изменения угла), а направление параллельно оси вращения, причем так, что имеет место правило буравчика. Итак, мы получили, что υ = [w ´ r]. Ориентация этих трех векторов показана на рис. 3.2. в направлении скорости –
в направлении скорости –  t (тангенциальное ускорение); в перпендикулярном направлении –
t (тангенциальное ускорение); в перпендикулярном направлении –  (3.6)
(3.6) , а t =
, а t =  , а n =
, а n = 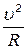 .
.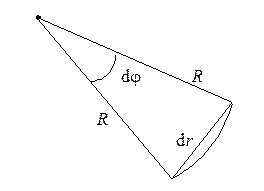 Поскольку вращательное движение может быть описано не только в угловых переменных, но и в линейных, установим между ними связь.
Поскольку вращательное движение может быть описано не только в угловых переменных, но и в линейных, установим между ними связь. , тогда
, тогда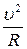 , тогда
, тогда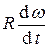 ,
,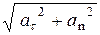 , тогда
, тогда . (3.10)
. (3.10)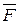 . Это векторная величина. Сила представляет собой обобщенную замену реальных взаимодействий между телами.
. Это векторная величина. Сила представляет собой обобщенную замену реальных взаимодействий между телами.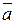 , величина которого пропорциональна результирующей силе
, величина которого пропорциональна результирующей силе  .(4.2)
.(4.2)

