Регрессионные модели с линейной структурой

· Полиномиальная регрессия. Распространенной “нелинейной” моделью является модель полиномиальной регрессии. Термин нелинейная заключен в кавычки, поскольку эта модель линейна по своей природе. Например, предположим, что вы измеряете в обучающем эксперименте связь физиологического возбуждения объектов и их производительности в задаче слежения за целями. На основании хорошо известного закона Йеркса-Додсона, можно ожидать нелинейной зависимости между уровнем возбуждения и производительностью. Это предположение можно выразить следующим уравнением регрессии:

· Производительность = a + b₁*Возбуждение + b₂*Возбуждение²

· В этом уравнении, a представляет свободный член, а b₁ и b₂ коэффициенты регрессии. Нелинейность этой модели выражается членом Возбуждение². Однако, в сущности, модель по-прежнему линейна, за исключением того, что при ее оценивании нам придется возводить наблюдаемый уровень возбуждения в квадрат. Для оценивания коэффициентов регрессии этой модели можно использовать фиксированное нелинейное оценивание. Такие модели, где мы составляем линейное уравнение из некоторых преобразований независимых переменных, относятся к моделям нелинейным по переменным.

· Модели, нелинейные по параметрам. Для сравнения с предыдущим примером рассмотрим зависимость между возрастом человека (переменная x) и его скоростью роста (переменная y). Очевидно, что соотношение между этими двумя переменными на первом году человеческой жизни (когда происходит наибольший рост) сильно отличается от соотношения во взрослом возрасте (когда человек почти не растет). Поэтому, эту зависимость лучше представить в виде какой-нибудь экспоненциальной функции с отрицательным показателем степени:

· Рост = exp(-b₁*Возраст)

· Если вы построите на графике оценку для коэффициента регрессии, то вы получите кривую следующего вида:

·

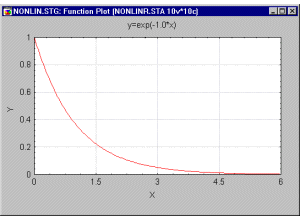
· Отметим, что эта модель по своей природе больше не является линейной, т.е. выражение, написанное сверху, не представимо в виде простой регрессионной модели с некоторыми преобразованиями независимых переменных. Такие модели называются нелинейными по параметрам.

· Сведение нелинейных моделей к линейным. В общем случае, всегда, когда регрессионная модель может быть сведена к линейной модели, этому способу отдается предпочтение (при оценивании соответствующей модели). Модель линейной множественной регрессии (см. Множественная регрессия) наиболее просто понимаема с точки зрения математики и, с практической точки зрения, наиболее проста для толкования. Поэтому, возвращаясь к простой экспоненциальной регрессионной модели Скорости роста как функции Возраста, описанной раньше, мы можем преобразовать это нелинейное уравнение в линейное, прологарифмировав обе части уравнения, получив:

· log(Рост) = -b₁*Возраст

· Если теперь заменить log(Рост)) на y, мы получим стандартную модель линейной регрессии, как уже было показано раньше (без свободного члена, который был опущен для простоты изложения). Таким образом, для оценивания взаимоотношения возраста и скорости роста вы можете прологарифмировать данные о скорости роста (например, воспользовавшись преобразованиями таблиц данных с помощью формул), а затем использовать Множественную регрессию, получив при этом интересующий нас коэффициент регрессии b₁.

· Адекватность модели. Конечно, используя “неправильное” преобразование, можно прийти к неадекватной модели. Поэтому, после ”линеаризации” модели, наподобие только что показанной, очень важно провести подробное изучение статистик остатков, вычисляемых с помощью Множественной регрессии.

·

· Существенно нелинейные регрессионные модели

· Для некоторых регрессионных моделей, которые не могут быть сведены к линейным, единственным способом для исследования остается Нелинейное оценивание. В приведенном выше примере для скорости роста, мы специально “забыли ” о случайной ошибке в зависимой переменной. Конечно, на скорость роста влияют множество других факторов (кроме возраста), и нам следует ожидать значительных случайных отклонений (остатков) от предложенной нами кривой. Если добавить эту ошибку или остаточную изменчивость, нашу модель можно переписать следующим образом:

· Рост = exp(-b₁*Возраст) + ошибка

· Аддитивная ошибка. В этой модели предполагается, что случайная ошибка не зависит от возраста, т.е., остаточная изменчивость одинакова для всех возрастов. Поскольку ошибка в этой модели аддитивна, т.е. просто прибавляется к точному значению скорости роста, мы больше не можем линеаризовать эту модель простым логарифмированием обеих частей. Если бы мы снова прологарифмировали входные данные о скорости роста и подобрали простую линейную модель, мы заметили бы, что остатки больше не являются равномерно распределенными вокруг значений переменной возраст; и поэтому, стандартный линейный регрессионный анализ (с помощью Множественной регрессии) больше не применим. Единственным способом оценивания параметров модели остается использование Нелинейного оценивания.

· Мультипликативная ошибка. В “оправдание” предыдущего примера заметим, что в данном случае постоянство вариации случайной ошибки в любом возрасте мало вероятно, т.е., предположение об аддитивности ошибки не слишком реалистично. Правдоподобнее, что изменения скорости роста более случайны и непредсказуемы в раннем возрасте, чем в позднем, когда рост практически останавливается. Поэтому, более реалистичной моделью, включающей ошибку, будет:

· Рост = exp(-b₁*Возраст) * ошибка

· На словах это означает, что чем больше возраст, тем меньше множитель exp(-b1*Возраст), и, следовательно, тем меньше будет разброс результирующей ошибки. Если же вы теперь прологарифмируете обе части нашего уравнения, то остаточная ошибка перейдет в свободный член линейного уравнения, т.е., аддитивный фактор, и вы сможете продолжить и оценить b1 пользуясь стандартную множественную регрессию.

· Log (Рост) = -b₁*Возраст + ошибка

· Теперь мы рассмотрим некоторые регрессионные модели (нелинейные по параметрам), которые не могут быть сведены к линейным простым преобразованием начальных данных.

· Общая модель роста. Общая модель роста похожа на рассмотренный ранее пример:

· y = b₀ + b₁*exp(b₂*x) + ошибка

· Эта модель обычно используется при изучении различных видов роста (y), когда скорость роста в любой момент времени (x) пропорциональна оставшемуся приросту. Параметр b₀ в этой модели представляет максимальное значение скорости роста. Типичным примером ее адекватного использования служит описание концентрации вещества (например, в воде) в виде функции времени.

· Модели бинарных откликов: пробит и логит. Нередко зависимая переменная - переменная отклика бинарна по своей природе, т.е. может принимать только два значения. Например, пациент может выздороветь, а может и нет, кандидат на должность может пройти, а может провалить тест при приеме на работу, подписчики журнала могут продлить, а могут не продлевать подписку, купоны скидок могут быть использованы, а могут быть и не использованы и т.п. Во всех этих случаях нас может заинтересовать поиск зависимости между одной или несколькими “непрерывными” переменными и одной, зависящей от них бинарной переменной.

· Использование линейной регрессии. Конечно, можно использовать стандартную множественную регрессию и вычислить стандартные коэффициенты регрессии. Например, если рассматривается продление журнальной подписки, можно задать переменную y со значениями 1 ’ и 0 ’, где 1 означает, что соответствующий подписчик продлил подписку, а 0, что он отказался от продления. Однако здесь возникает проблема: Множественная регрессия не “знает”, что переменная отклика бинарна по своей природе. Поэтому, это неизбежно приведет к модели с предсказываемыми значениями большими 1 и меньшими 0. Но такие значения вообще не допустимы для первоначальной задачи, таким образом, множественная регрессия просто игнорирует ограничения на диапазон значений для y.

· Непрерывные функции отклика. Задача регрессии может быть сформулирована иначе: вместо предсказания бинарной переменной, мы предсказываем непрерывную переменную со значениями на отрезке [0,1]. Наибольшее распространение в этой области получили регрессионные модели логит и пробит. \

Метод наименьших квадратов (МНК, англ. Ordinary Least Squares, OLS) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.

• МНК - минимизируется сумма квадратов отклонений реально наблюдаемых Y от их оценок Y ^ (имеются в виду оценки с помощью прямой линии, претендующей на то, чтобы представлять искомую регрессионную зависимость):

∑ _k = ∑ ^M (Y _k − Y _k ^) ² → min,

M — объём выборки.

Используется один из методов оптимизации, смотри библиотеки программ.

20. Методы оценки качества линейных и нелинейных регрессионных моделей: адекватность, значимость коэффициентов.