

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...
Топ:
Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Интересное:
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
ПРЕДЕЛАМИ (1-ГО РОДА).
Как следует из названия, к несобственным интегралам с бесконечными пределами относятся интегралы в тех случаях, если хотя бы один из пределов интегрирования равен  , т. е. интегралы вида
, т. е. интегралы вида
 ,
,  ,
,  .
.
Рассмотрим интеграл  .
.
Определение. Пусть функция f(x) задана на промежутке [a,∞) и для любого А≥а существует интеграл вида  . Несобственным интегралом с бесконечными пределами (или 1-го рода) называется предел
. Несобственным интегралом с бесконечными пределами (или 1-го рода) называется предел
 и обозначается
и обозначается  .
.
Определение. Если предел  существует и конечен, то несобственный интеграл 1-го рода называется сходящимся, в противном случае (т.е. равен бесконечности или не существует) – расходящимся.
существует и конечен, то несобственный интеграл 1-го рода называется сходящимся, в противном случае (т.е. равен бесконечности или не существует) – расходящимся.
Аналогично, несобственный интеграл вида  сходится, если существует и конечен предел вида
сходится, если существует и конечен предел вида  .
.
Для исследования сходимости несобственного интеграла вида  необходимо воспользоваться свойством аддитивности по области, а затем для каждого слагаемого отдельно вычислить предел
необходимо воспользоваться свойством аддитивности по области, а затем для каждого слагаемого отдельно вычислить предел

где с - любое вещественное число.
Примеры.
1. 

2. 




Замечание.
Так как в обоих примерах интеграла имеют конечные значения, то они сходятся.
Рассмотрим примеры расходящихся интегралов.
3. 

Так как для функций sin x и cos x на бесконечности предела не существует, то рассматриваемый интеграл расходится
4. 
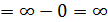
Следовательно, интеграл расходится.
На несобственные интегралы с бесконечными пределами распространяются многие свойства определенных интегралов, за исключением одного: интеграл от константы, не равной нулю, по бесконечному интервалу всегда расходится.
Геометрический смысл несобственного интеграла первого рода
Рассмотрим интеграл вида  . Будем считать, что функция f(x) неотрицательна. Тогда рассматриваемый интеграл численно равен площади неограниченной справа криволинейной трапеции, изображенной ниже
. Будем считать, что функция f(x) неотрицательна. Тогда рассматриваемый интеграл численно равен площади неограниченной справа криволинейной трапеции, изображенной ниже
|
|


 Y
Y
 |

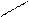 y=f(x)
y=f(x)
 |


 X
X
O x=a
Для вычисления несобственного интеграла 1-го рода применяют формулу Ньютона-Лейбница. Однако, если вычисление первообразной затруднительно, то выясняют только вопрос о сходимости или расходимости интеграла, оценивая его значение.
Для этого используют теоремы о сравнении.
Теорема 1.
Если для любого x (при x≥a) выполняется неравенство
0≤f(x)≤g(x)
и если интеграл  сходится, то интеграл
сходится, то интеграл  тоже сходится, при этом выполняется следующее неравенство
тоже сходится, при этом выполняется следующее неравенство
 ≤
≤  .
.
Теорема 2.
Если для любого x (при x≥a) выполняется неравенство
0≤g(x)≤f(x)
и если интеграл  расходится, то интеграл
расходится, то интеграл  тоже расходится, при этом выполняется следующее неравенство
тоже расходится, при этом выполняется следующее неравенство
 .
.
Теорема 3.
Если для любого x (при x≥a) существует предел
 ,
,
то интегралы  и
и 
сходятся или расходятся одновременно.
Замечания.
1. В заявленных теоремах рассматриваются интегралы от неотрицательных функций.
2. Для оценивания несобственных интегралов теорема 3 является самой удобной в использовании.
3. Условие теоремы 3 
означает, что заявленные функции не превосходят существенно друг друга на бесконечности, т.е.  при x →∞.
при x →∞.
4. Чаще всего исследуемый интеграл сравнивают с интегралом вида  , который сходится при p>1 и расходится при p≤1 (доказать эти утверждения самостоятельно).
, который сходится при p>1 и расходится при p≤1 (доказать эти утверждения самостоятельно).
Для того, чтобы определить степень знаменателя p, нужно вычислить предел подынтегральной функции на бесконечности, используя оценку этой функции степенными функциями. В последнем равенстве под пределом будет находиться требуемый одночлен xp. Рассмотрим конкретный пример.
Пример. Определить сходимость несобственного интеграла
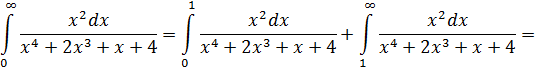

Свойство аддитивности по области представить несобственный интеграл в виде суммы двух слагаемых, первое – это определенный интеграл, т.е. имеет конечное значение, второе – это несобственный интеграл с новыми пределами интегрирования. Рассмотрим предел от подынтегральной функции
|
|


Заметим, что исходная подынтегральная функция и функция  будут стремиться к бесконечности с одинаковой скоростью, т.е. являются эквивалентными на бесконечности, и, следовательно, интегралы
будут стремиться к бесконечности с одинаковой скоростью, т.е. являются эквивалентными на бесконечности, и, следовательно, интегралы  будут сходиться или расходиться одновременно. Интеграл
будут сходиться или расходиться одновременно. Интеграл  будет сходиться, так как степень одночлена в знаменателе p=2 >1. Таким образом, интеграл
будет сходиться, так как степень одночлена в знаменателе p=2 >1. Таким образом, интеграл  также будет сходиться, т.е. будет конечен. Так как сумма двух конечных слагаемых - конечна, то исходный интеграл
также будет сходиться, т.е. будет конечен. Так как сумма двух конечных слагаемых - конечна, то исходный интеграл  <∞, т.е. будет сходиться.
<∞, т.е. будет сходиться.
Определение. Несобственный интеграл первого рода  называется абсолютно сходящимся, если сходится интеграл
называется абсолютно сходящимся, если сходится интеграл  .
.
Замечание.
Если неопределенный интеграл сходится абсолютно, то он тем более сходится.
Пример. Исследовать на сходимость интеграл  .
.
Так как функция cos x является знакопеременной, то и подынтегральная функция тоже знакопеременна. Проведем оценку этой функции
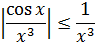
после чего рассмотрим новый несобственный интеграл  , так как степень одночлена в знаменателе p=3> 1, то он сходится, следовательно, сходится и интеграл
, так как степень одночлена в знаменателе p=3> 1, то он сходится, следовательно, сходится и интеграл  <∞. Исходя из этого, приходим к выводу, что исходный интеграл сходится абсолютно.
<∞. Исходя из этого, приходим к выводу, что исходный интеграл сходится абсолютно.
|
|
|

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!