Напряжение – численная мера распределения внутренних сил по плоскости поперечного сечения. Его используют при исследовании и определении внутренних сил любой конструкции.
Выделим на плоскости сечения площадку DA; по этой площадке будет действовать внутренняя сила DR. Величина отношения DR/DA=pср называется средним напряжением на площадке DA. Истинное напряжение в точке А получим устремив DA к нулю
Нормальные напряжения возникают, когда частицы материала стремятся отдалиться друг от друга или, наоборот, сблизиться. Касательные напряжения связаны со сдвигом частиц по плоскости рассматриваемого сечения.
 Очевидно, что
Очевидно, что 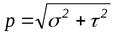 . Касательное напряжение в свою очередь может быть разложено по направлениям осей x и y (τzх, τzу). Размерность напряжений – Н/м2 (Па).
. Касательное напряжение в свою очередь может быть разложено по направлениям осей x и y (τzх, τzу). Размерность напряжений – Н/м2 (Па).
 1 7. Понятие о напряжениях. Нормальные и касательные напряжения.
1 7. Понятие о напряжениях. Нормальные и касательные напряжения.
Внутренние силовые факторы. Метод сечений. Эпюры. Выражение внутренних силовых факторов через нормальные и касательные напряжения.
Внутренние силовые факторы
В процессе деформации бруса, под нагрузкой происходит изменение взаимного расположения элементарных частиц тела, в результате чего в нем возникают внутренние силы.
По своей природе внутренние силы представляют собой взаимодействие частиц тела, обеспечивающее его целостность и совместность деформаций.
Чтобы численно установить величину внутренних сил пользуются методом сечений.
Метод сечений сводится к четырем действиям:
1. Разрезают (мысленно) тело плоскостью  в том месте, где нужно определить внутренние силы (рис. 7);
в том месте, где нужно определить внутренние силы (рис. 7);

Рис. 7
2. Отбрасывают любую отрезанную часть тела (желательно наиболее сложную), а ее действие на оставшуюся часть заменяют внутренними силами, чтобы оставшаяся исследуемая часть находилась в равновесии (рис.8);

Рис. 8
3. Приводят систему сил к одной точке (как правило, к центру тяжести сечения) и проецируют главный вектор и главный момент системы внутренних сил на нормаль к плоскости (ось  ) и главные центральные оси сечения (
) и главные центральные оси сечения ( и
и  ).
).
Полученные силы (N, Qy, Qz) (рис. 9) и моменты (Мк, Мy, Mz) называют внутренними силовыми факторами в сечении

Рис. 9
Для внутренних силовых факторов приняты следующие названия:
 - продольная или осевая сила;
- продольная или осевая сила;
 и
и  - поперечные силы;
- поперечные силы;
 - крутящий момент;
- крутящий момент;
 и
и  - изгибающие моменты.
- изгибающие моменты.
4. Находят внутренние силовые факторы, составляя шесть уравнений равновесия статики для рассматриваемой части рассеченного тела.
Эпю́ра (фр. epure — чертёж) — особый вид графика, показывающий распределение величины нагрузки на объект. Например, для стержня продольная ось симметрии берётся за область определения и составляются эпюры для сил, напряжений и разных деформаций в зависимости от абсциссы.
Расчёт эпюр напряжения является базовой задачей такой дисциплины, как сопротивление материалов. В частности, только при помощи эпюры возможно определить максимально допустимую нагрузку на материал.
Для построения ординаты эпюры M в каком либо сечении стержня
необходимо выполнить следующие две операции.
1. С помощью уравнения равновесия ∑M(слева)= 0 для левой отсеченной
части стержневой системы (или ∑M(справа) = 0 для правой части) подсчитать
численное значение изгибающего момента в сечении.
2. Отложить найденное численное значение в виде ординаты перпендикулярно оси стержня со стороны растянутого волокна стержня.
Численное значение изгибающего момента в сечении равно численному значению алгебраической суммы моментов всех сил, действующих на стержневую систему с любой одной из сторон сечения, взятых относительно точки на оси сечения.
Составляющую, лежащую в сечении в данной площадке обозначается через  и называется касательным напряжением.
и называется касательным напряжением.
Нормальное напряжение, направленное от сечения, считают положительным, направленное к сечению – отрицательным.
Нормальные напряжения возникают, когда под действием внешних сил частицы, расположенные по обе стороны от сечения, стремятся удалиться одна от другой или сблизиться. Касательные напряжения возникают, когда частицы стремятся сдвинуться одна относительно другой в плоскости сечения.
Касательное напряжение можно разложить по координатным осям на две составляющие  и
и  (рис. в) Первый индекс при
(рис. в) Первый индекс при  показывает, какая ось перпендикулярна сечению, второй – параллельно какой оси действует напряжение. Если в расчетах направление касательного напряжения не имеет значения, его обозначают без индексов.
показывает, какая ось перпендикулярна сечению, второй – параллельно какой оси действует напряжение. Если в расчетах направление касательного напряжения не имеет значения, его обозначают без индексов.






 Очевидно, что
Очевидно, что 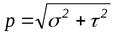 . Касательное напряжение в свою очередь может быть разложено по направлениям осей x и y (τzх, τzу). Размерность напряжений – Н/м2 (Па).
. Касательное напряжение в свою очередь может быть разложено по направлениям осей x и y (τzх, τzу). Размерность напряжений – Н/м2 (Па). 1 7. Понятие о напряжениях. Нормальные и касательные напряжения.
1 7. Понятие о напряжениях. Нормальные и касательные напряжения. в том месте, где нужно определить внутренние силы (рис. 7);
в том месте, где нужно определить внутренние силы (рис. 7);

 ) и главные центральные оси сечения (
) и главные центральные оси сечения ( и
и  ).
).
 - продольная или осевая сила;
- продольная или осевая сила; и
и  - поперечные силы;
- поперечные силы; - крутящий момент;
- крутящий момент; и
и  - изгибающие моменты.
- изгибающие моменты. и называется касательным напряжением.
и называется касательным напряжением. и
и  (рис. в) Первый индекс при
(рис. в) Первый индекс при 



