

30. 

31. мат ожидание и его св-ва







32. моменты случайных велечин




32. дисперсия св-ва


33распределение бернулли пуассона геометрическое
Закон распределения Бернулли, его определение, свойства и примеры.
Дискретная случайная величина X имеет биномиальное распределение (или распределена по биномиальному закону), если она принимает значения 0, 1, 2, …, n, с соответствующими вероятностями:
 , где
, где  ,
, 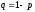 ,
,  .
.
Математическое ожидание и дисперсия случайной величины X, имеющей биномиальное распределение, находятся по формулам:
 .
.
Из формулы Бернулли следует, что случайная величина  – число наступлений события
– число наступлений события  в
в  независимых испытаниях (
независимых испытаниях (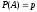 ) – распределена по биномиальному закону.
) – распределена по биномиальному закону.
21. Биномиальный закон распределения, его определение, свойства и примеры.
Пусть производится n независимых испытаний, в каждом из которых событие A может появиться или не появиться. Вероятность наступления события во всех испытаниях постоянна и равна p (следовательно, вероятность непоявления q = 1 - p).
Рассмотрим случайную величину X – число появлений события A в этих испытаниях. Случайная величина X принимает значения 0,1,2,…n с вероятностями, вычисленными по формуле Бернулли: 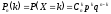 , где k = 0,1,2,…n.
, где k = 0,1,2,…n.
Определение: Биномиальным называют раcпределение вероятностей, определяемое формулой Бернулли.
Пример. По мишени производится три выстрела, причем вероятность попадания при каждом выстреле равна 0,8. Рассматривается случайная величина X – число попаданий в мишень. Найти ее ряд распределения.
Решение: Случайная величина X принимает значения 0,1,2,3 с вероятностями, вычисленными по формуле Бернулли, где n = 3, p = 0,8 (вероятность попадания), q = 1 - 0,8 = = 0,2 (вероятность непопадания).
Тогда
 ,
,



Таким образом, ряд распределения имеет следующий вид:
Пользоваться формулой Бернулли при больших значениях n достаточно трудно, поэтому для подсчета соответствующих вероятностей используют локальную теорему Лапласа, которая позволяет приближенно найти вероятность появления события ровно k раз в n испытаниях, если число испытаний достаточно велико.
22.Закон распределения Пуассона, его определение, свойства и примеры.
Определение. Будем говорить, что случайная величина ε распределена по закону Пуассона с параметром λ, еслиона принимает значения из множества { 0,1,…,n, …} с вероятностямиP{ ε =m} = (λm/m!)*e-λ.
33. Теорема. Если случайная величина ε распределена по закону Пуассона с параметром λ, то и математическое ожидание, и дисперсия этой случайной величины равны параметру λ.
Свойства распределения Пуассона:
1.  .
.
33Действительно: 
2.  .
.
3. если  , то из биномиального распределения следует закон распределения Пуассона.
, то из биномиального распределения следует закон распределения Пуассона.
Замечание. По формуле Пуассона можно вычислить вероятность того, что число событий, происшедших за время  равно
равно  , если события образуют пуассоновский поток, причём
, если события образуют пуассоновский поток, причём  – интенсивность потока, то есть среднее число событий, которые появляются в единицу времени:
– интенсивность потока, то есть среднее число событий, которые появляются в единицу времени:
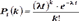 .
.
Геометрическое распределение, его определение, свойства и примеры.
Пусть проводятся независимые испытания, каждое испытание может иметь два исхода: удача с вероятностью p и неудача с вероятностью q = 1 - p. Введем в рассмотрение случайную величину X — число испытаний до первого появления удачи. Эта случайная величина может принимать значения 1, 2, 3, 4 и так далее до бесконечности. Когда говорят, что случайная величина X имеет значение k, то это означает, что первые k - 1 испытание закончились неудачей, а k-ое испытание стало удачным. Вероятность того, что в серии независимых испытаний будет вначале k - 1 неудач, а в k-ое испытание — удача, равна  . Таким образом мы получили закон распределения случайной величины X: значению k случайной величины соответствует вероятность
. Таким образом мы получили закон распределения случайной величины X: значению k случайной величины соответствует вероятность  . Этот закон распределения и называется геометрическим распределением. Название происходит из того, что величина
. Этот закон распределения и называется геометрическим распределением. Название происходит из того, что величина  представляет собой геометрическую прогрессию, с первым членом p и знаменателем q.Изучим теперь свойства этого распределения. С ростом k вероятности убывают. Используя формулу для суммы членов геометрической прогрессии, можем записать:
представляет собой геометрическую прогрессию, с первым членом p и знаменателем q.Изучим теперь свойства этого распределения. С ростом k вероятности убывают. Используя формулу для суммы членов геометрической прогрессии, можем записать:  , то есть условие, что сумма всех вероятностей в законе распределения равна единице, выполнено. Вычислим теперь математическое ожидание и дисперсию. По определению математического ожидания имеем:
, то есть условие, что сумма всех вероятностей в законе распределения равна единице, выполнено. Вычислим теперь математическое ожидание и дисперсию. По определению математического ожидания имеем:  . Для вычисления суммы воспользуемся следующим приемом — заменим
. Для вычисления суммы воспользуемся следующим приемом — заменим  на
на  и вынесем производную за знак суммы, в итоге получим:
и вынесем производную за знак суммы, в итоге получим:  . Оставшаяся сумма представляет собой сумму членов геометрической прогрессии и равна
. Оставшаяся сумма представляет собой сумму членов геометрической прогрессии и равна  . Вычисляя производную, запишем:
. Вычисляя производную, запишем:  . Аналогично можно получить выражение для
. Аналогично можно получить выражение для  :
:  . Заменяя сумму на 33ее значение
. Заменяя сумму на 33ее значение  , вычисляем:
, вычисляем:  . Таким образом, имеем выражение для дисперсии:
. Таким образом, имеем выражение для дисперсии:  .
.
34. равномерное и показат распределение 


35. неравенство Маркова и Чебышева. Виды сходимости случ посл


Как и в математическом анализе, в теории вероятностей приходится иметь дело с разными видами сходимости случайных величин. Рассмотрим основные виды сходимости: по вероятности; с вероятностью 1; в среднем порядка s; по распределению.
Пусть X1, X2,... - последовательность случайных величин задана на вероятностном пространстве < W,F,P>. Пусть на этом пространстве задана также и случайная величина X.
Определение 1. Последовательность случайных величин X1,...,Xn,... называется сходящейся по вероятности к случайной величине X (обозначение:  ), если для любого e>0 ("e>0) существует:
), если для любого e>0 ("e>0) существует:
 P{|Xn-X|>e}=0, n®¥ (1)
P{|Xn-X|>e}=0, n®¥ (1)
Определение 2. Последовательность случайных величин X1,X2,... называется сходящейся с вероятностью единица (почти наверное, почти всюду) к случайной величине X, если
 (2)
(2)
т.е. если множество исходов w, для которых Xn(w) не сходятся к X(w), имеет нулевую вероятность. Этот вид сходимости обозначают следующим образом: 
Определение 3. Последовательность случайных величин X1, X2,... называется сходящейся в среднем порядка s, 0 < s < ¥, к случайной величине X, если
M |Xn-X|s®0, n®¥ или  (3)
(3)
Если s = 2, то сходимость (3) называют сходимостью в среднем квадратическом и используют формулу.
 (4)
(4)
Определение 4. Последовательность случайных величин X1, X2,... называется сходящейся по распределению к случайной величине, если во всех точках x, где функция распределения FX(x) - непрерывна, выполняется условие
 (5)Это обозначается так:
(5)Это обозначается так:  ;
;  .
.
Замечание 1. О сходимости по распределению можно говорить и в том случае, если {Xn} и X заданы на разных вероятностных пространствах.
Замечание 2. Сходимость по вероятности, почти всюду, в среднем порядка s применима и к неслучайным величинам.
36 
Центра́льные преде́льные теоре́мы (Ц. П. Т.) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.


38 нормальный закон распределения и его свойсвтва
Нормальный закон распределения
Результаты, полученные при измерении той или иной величины, нельзя принять из-за ряда случайностей за достоверные (действительные значения измеряемых величин). Тогда приходится говорить о вероятности того или иного значения этих величин и определить их. Вероятность события - это количественная оценка объективной возможности появления данного события. Вероятность достоверных событий равна 1. Например, после ночи наступит утро. Вероятность невозможных событий равна 0. Случайные события имеют вероятность (p) больше 0, но меньше 1, т.е. 0 £ p £ 1.
Если число всех равновероятных событий n и появление желательного результата возможно m раз, то p* = m/n (частота появления события).
Как было показано Я. Бернулли, частота появления события будет сколь угодно мало отличаться от вероятности при большом числе n, т.е. p =  p*, p - статистическая вероятность события.
p*, p - статистическая вероятность события.
Всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями, есть закон распределения случайной величины.
Закон распределения случайной величины может быть задан в разных формах:а) ряд распределения (для дискретных величин);б) функция распределения;в) кривая распределения (для непрерывных величин).
Кривая нормального распределения была дана немецким математиком К.Ф.Гауссом в 1821 г.: 
где у (xi) - ордината кривой нормального распределения (плотность вероятности случайной величины); x - значение случайной величины; m - истинное значение величины (среднее арифметическое или математическое ожидание случайной величины); s - среднее квадратическое отклонение; e - основание натуральных логарифмов (e = 2.7183).
Основные свойства нормального распределения.
1. Функция плотности распределения определена на всей числовой оси Ох, то есть каждому значению х соответствует вполне определённое значение функции.
2. При всех значениях х (как положительных, так и отрицательных) функция плотности принимает положительные значения, то есть нормальная кривая расположена над осью Ох.
3. Предел функции плотности при неограниченном возрастании х равен нулю,  .
.
4. Функция плотности нормального распределения в точке  имеет максимум
имеет максимум  .
.
5. График функции плотности  симметричен относительно прямой
симметричен относительно прямой  .
.
6. Кривая распределения имеет две точки перегиба с координатами  и
и  .
.
7. Мода и медиана нормального распределения совпадают с математическим ожиданием а.
8. Форма нормальной кривой не изменяется при изменении параметра а.
9. Коэффициенты асимметрии и эксцесса нормального распределения равны нулю.
39. гамма и хи квадрат распределение
Гамма-распределение является двухпараметрическим распределением. Оно занимает важное место в теории надежности. Плотность распределения имеет ограничение с одной стороны (0 ≤ х ≤ ∞). Если параметр α формы кривой распределения принимает целое значение, то это свидетельствует о вероятности появления такого же числа событий (например, отказов) при условии, что они независимы и появляются с постоянной интенсивностью λ.
Гамма-распределение широко применяют при описании появления отказов стареющих элементов, времени восстановления, наработки на отказ резервированных систем. При различных параметрах гамма-распределение принимает разнообразные формы, что и объясняет его широкое применение.
Плотность вероятности гамма-распределения определяется равенствами
 при x ≥0; (38)
при x ≥0; (38)
f (x) = 0 при x <0,
где λ >0, α >0;
 (39)
(39)
Кривая изменения плотности распределения приведена на рис. 5.
Функция распределения
 при x ≥0; (40)
при x ≥0; (40)
F (x) = 0 при х < 0.
Математическое ожидание и дисперсия соответственно равны:
 (41)
(41)
При α <1 интенсивность отказов монотонно убывает (что соответствует периоду приработки изделия), при α >1 — возрастает (что характерно для периода изнашивания и старения элементов).

Рис. 5. Кривые плотности гамма-распределения
При α =1 гамма-распределение совпадает с экспоненциальным распределением, при α>10 гамма-распределение приближается к нормальному закону. Если α принимает значения
произвольных целых положительных чисел, то такое гамма-распределение называют распределением Эрланга. Если λ=1/2, а значение α кратно 1/2, то гамма-распределение совпадает с распределением χ2 (хи-квадрат).
) Распределение (хи-квадрат) с n степенями свободы — это распределение суммы квадратов n независимых стандартных нормальных случайных величин.
Распределение  (хи – квадрат) – распределение случайной величины (причем математическое ожидание каждой из них равно 0, а среднее квадратическое отклонение-1)
(хи – квадрат) – распределение случайной величины (причем математическое ожидание каждой из них равно 0, а среднее квадратическое отклонение-1)

где случайные величины  независимы и имеют одно и тоже распределение
независимы и имеют одно и тоже распределение  . При этом число слагаемых, т.е.
. При этом число слагаемых, т.е.  , называется "числом степеней свободы" распределения хи-квадрат. Число хи-квадрат опредляется одни параметром-числом степеней свободы. С увеличением числа степеней свободы распределение медленно приближается к нормальному.
, называется "числом степеней свободы" распределения хи-квадрат. Число хи-квадрат опредляется одни параметром-числом степеней свободы. С увеличением числа степеней свободы распределение медленно приближается к нормальному.
Тогда сумма их квадратов
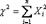 является случайной величиной, распределенной по так называемому закону «хи-квадрат» с k = n степенями свободы; если же слагаемые связаны каким-либо соотношением (например,
является случайной величиной, распределенной по так называемому закону «хи-квадрат» с k = n степенями свободы; если же слагаемые связаны каким-либо соотношением (например,  ), то число степеней свободы k = n –
), то число степеней свободы k = n –
40 Определение случайной величины. Многие случайные события могут быть оценены количественно случайными величинами,
Случайной называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств.
Случайными величинами являются: число больных на приеме у врача, число студентов в аудитории, число рождений в городе, продолжительность жизни отдельного человека, скорость молекулы, температура воздуха, погрешность в измерении какой-либо величины и др. Если пронумеровать шары в урне примерно так, как это делают при разыгрывании тиража лото, то произвольное вынимание шара из урны покажет число, являющееся случайной величиной.
Различают дискретные и непрерывные случайные величины.
Случайная величина называется дискретной, если она принимает счетное множество значений: число букв на произвольной странице книги, энергия электрона в атоме, число волос на голове человека, число зерен в колосьях, число молекул в выделенном объеме газа и т. п.
Непрерывная случайная величина принимает любые значения внутри некоторого интервала: температура тела, масса зерен в колосьях пшеницы, координата места попадания пули в цель (принимаем пулю за материальную точку) и др.
Распределение дискретной случайной величины. Дискретная случайная величина считается заданной, если указаны ее возможные значения и соответствующие им вероятности. Обозначим дискретную случайную величину X, ее значения хг х2,..., а вероятности Р(х1) — p1, Р(х2) = р2 и т. д. Совокупность X и Р называется распределением дискретной случайной величины (табл. 1).
Таблица 1
| X
| Х1
| Х2
| Х3
| Х4
| Х5
| …
|
| Р
| p1
| p2
| рз
| р4
| р5
| …
|
 Так как все возможные значения дискретной случайной величины представляют полную систему (см. § 2.1), то сумма вероятностей равна единице:
Так как все возможные значения дискретной случайной величины представляют полную систему (см. § 2.1), то сумма вероятностей равна единице:
Здесь предполагается, что дискретная случайная величина имеет п значений. Выражение (2.9) называется условием нормировки.
Распределение и характеристики непрерывной случайной величины. Непрерывную случайную величину нельзя задать тем же законом распределения, что и дискретную. В этом случае поступают следующим образом.
Пусть dP — вероятность того, что непрерывная случайная величина X принимает значения между х и х + dx. Очевидно, что чем больше интервал dx, тем больше и вероятность dP: dP ¥ dx. Кроме того, вероятность должна зависеть и от самой случайной величины, вблизи которой расположен интервал, поэтому
dP = f(x)dx, (2.15) где f(x) — плотность вероятности, или функция распределения вероятностей. Она показывает, как изменяется вероятность, отнесенная к интервалу dx случайной величины, в зависимости от значения самой этой величины:
f(x) = dP/dx. Интегрируя выражение (2.15) в соответствующих пределах, находим вероятность того, что случайная величина принимает какое-либо значение в интервале (ab):
 (2.17) Условие нормировки для непрерывной случайной величины имеет вид
(2.17) Условие нормировки для непрерывной случайной величины имеет вид
 (2.18) Наряду с плотностью вероятности в математике используют также и функцию распределения непрерывной случайной величины:
(2.18) Наряду с плотностью вероятности в математике используют также и функцию распределения непрерывной случайной величины:
 (2.19) Как видно из (2.19), эта функция равна вероятности того, что случайная величина принимает значения, меньшие х:
(2.19) Как видно из (2.19), эта функция равна вероятности того, что случайная величина принимает значения, меньшие х:

41Пусть случайный вектор  имеет вектор средних
имеет вектор средних  и невырожденную матрицу ковариаций
и невырожденную матрицу ковариаций  , составленную из элементов
, составленную из элементов  . Говорят, что вектор
. Говорят, что вектор 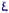 имеет нормальное распределение
имеет нормальное распределение  в
в  , если плотность этого вектора равна
, если плотность этого вектора равна

Квадратичная форма  в показателе экспоненты равна
в показателе экспоненты равна
Замечание 24. 
Вектор, составленный из нормальных случайных величин, не обязательно имеет многомерное нормальное распределение. Так, вектор  имеет вырожденную матрицу ковариаций
имеет вырожденную матрицу ковариаций  , если
, если  , и не имеет плотности в
, и не имеет плотности в  .
.
Поэтому в условиях следующей теоремы существование совместной нормальной плотности координат вектора обязательно. Теорема 14. Пусть вектор  имеет многомерное нормальное распределение
имеет многомерное нормальное распределение  . Координаты этого вектора независимы тогда и только тогда, когда они некоррелированы, т.е. когда матрица ковариаций
. Координаты этого вектора независимы тогда и только тогда, когда они некоррелированы, т.е. когда матрица ковариаций 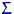 диагональна.
диагональна.
Замечание 25.
Следовало бы крикнуть «ура!»: свойство, о котором мы давно мечтали, — чтобы независимость следовала из некоррелированности, — имеет все же место. Но только для наборов случайных величин с нормальным совместным распределением, и это — очередное изумительное качество нормального распределения.
Доказательство. Только в случае диагональной матрицы 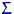 с элементами
с элементами  квадратичная форма (37) превращается в сумму квадратов
квадратичная форма (37) превращается в сумму квадратов

и многомерная плотность распадается в произведение плотностей координат.
Q.D.E.
Надеюсь, читатель поверит следующей теореме без доказательства, будучи в состоянии доказать ее, как и в одномерном случае, с помощью многомерных характеристических функций.


















 , где
, где  ,
, 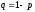 ,
,  .
. .
. – число наступлений события
– число наступлений события  в
в  независимых испытаниях (
независимых испытаниях (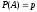 ) – распределена по биномиальному закону.
) – распределена по биномиальному закону.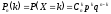 , где k = 0,1,2,…n.
, где k = 0,1,2,…n. ,
,


 .
.
 .
. , то из биномиального распределения следует закон распределения Пуассона.
, то из биномиального распределения следует закон распределения Пуассона. равно
равно  , если события образуют пуассоновский поток, причём
, если события образуют пуассоновский поток, причём  – интенсивность потока, то есть среднее число событий, которые появляются в единицу времени:
– интенсивность потока, то есть среднее число событий, которые появляются в единицу времени: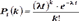 .
. . Таким образом мы получили закон распределения случайной величины X: значению k случайной величины соответствует вероятность
. Таким образом мы получили закон распределения случайной величины X: значению k случайной величины соответствует вероятность  . Этот закон распределения и называется геометрическим распределением. Название происходит из того, что величина
. Этот закон распределения и называется геометрическим распределением. Название происходит из того, что величина  представляет собой геометрическую прогрессию, с первым членом p и знаменателем q.Изучим теперь свойства этого распределения. С ростом k вероятности убывают. Используя формулу для суммы членов геометрической прогрессии, можем записать:
представляет собой геометрическую прогрессию, с первым членом p и знаменателем q.Изучим теперь свойства этого распределения. С ростом k вероятности убывают. Используя формулу для суммы членов геометрической прогрессии, можем записать:  , то есть условие, что сумма всех вероятностей в законе распределения равна единице, выполнено. Вычислим теперь математическое ожидание и дисперсию. По определению математического ожидания имеем:
, то есть условие, что сумма всех вероятностей в законе распределения равна единице, выполнено. Вычислим теперь математическое ожидание и дисперсию. По определению математического ожидания имеем:  . Для вычисления суммы воспользуемся следующим приемом — заменим
. Для вычисления суммы воспользуемся следующим приемом — заменим  на
на  и вынесем производную за знак суммы, в итоге получим:
и вынесем производную за знак суммы, в итоге получим:  . Оставшаяся сумма представляет собой сумму членов геометрической прогрессии и равна
. Оставшаяся сумма представляет собой сумму членов геометрической прогрессии и равна  . Вычисляя производную, запишем:
. Вычисляя производную, запишем:  . Аналогично можно получить выражение для
. Аналогично можно получить выражение для  :
:  . Заменяя сумму на 33ее значение
. Заменяя сумму на 33ее значение  , вычисляем:
, вычисляем:  . Таким образом, имеем выражение для дисперсии:
. Таким образом, имеем выражение для дисперсии:  .
.




 ), если для любого e>0 ("e>0) существует:
), если для любого e>0 ("e>0) существует: P{|Xn-X|>e}=0, n®¥ (1)
P{|Xn-X|>e}=0, n®¥ (1) (2)
(2)
 (3)
(3) (4)
(4) (5)Это обозначается так:
(5)Это обозначается так:  ;
;  .
.


 p*, p - статистическая вероятность события.
p*, p - статистическая вероятность события.
 .
. имеет максимум
имеет максимум  .
. симметричен относительно прямой
симметричен относительно прямой  .
. и
и  .
. при x ≥0; (38)
при x ≥0; (38) (39)
(39) при x ≥0; (40)
при x ≥0; (40) (41)
(41)
 (хи – квадрат) – распределение случайной величины (причем математическое ожидание каждой из них равно 0, а среднее квадратическое отклонение-1)
(хи – квадрат) – распределение случайной величины (причем математическое ожидание каждой из них равно 0, а среднее квадратическое отклонение-1)
 независимы и имеют одно и тоже распределение
независимы и имеют одно и тоже распределение  . При этом число слагаемых, т.е.
. При этом число слагаемых, т.е.  , называется "числом степеней свободы" распределения хи-квадрат. Число хи-квадрат опредляется одни параметром-числом степеней свободы. С увеличением числа степеней свободы распределение медленно приближается к нормальному.
, называется "числом степеней свободы" распределения хи-квадрат. Число хи-квадрат опредляется одни параметром-числом степеней свободы. С увеличением числа степеней свободы распределение медленно приближается к нормальному.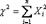 является случайной величиной, распределенной по так называемому закону «хи-квадрат» с k = n степенями свободы; если же слагаемые связаны каким-либо соотношением (например,
является случайной величиной, распределенной по так называемому закону «хи-квадрат» с k = n степенями свободы; если же слагаемые связаны каким-либо соотношением (например,  ), то число степеней свободы k = n –
), то число степеней свободы k = n – Так как все возможные значения дискретной случайной величины представляют полную систему (см. § 2.1), то сумма вероятностей равна единице:
Так как все возможные значения дискретной случайной величины представляют полную систему (см. § 2.1), то сумма вероятностей равна единице: (2.17) Условие нормировки для непрерывной случайной величины имеет вид
(2.17) Условие нормировки для непрерывной случайной величины имеет вид (2.18) Наряду с плотностью вероятности в математике используют также и функцию распределения непрерывной случайной величины:
(2.18) Наряду с плотностью вероятности в математике используют также и функцию распределения непрерывной случайной величины: (2.19) Как видно из (2.19), эта функция равна вероятности того, что случайная величина принимает значения, меньшие х:
(2.19) Как видно из (2.19), эта функция равна вероятности того, что случайная величина принимает значения, меньшие х:
 имеет вектор средних
имеет вектор средних  и невырожденную матрицу ковариаций
и невырожденную матрицу ковариаций  , составленную из элементов
, составленную из элементов  . Говорят, что вектор
. Говорят, что вектор 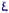 имеет нормальное распределение
имеет нормальное распределение  в
в  , если плотность этого вектора равна
, если плотность этого вектора равна
 в показателе экспоненты равна
в показателе экспоненты равна
 имеет вырожденную матрицу ковариаций
имеет вырожденную матрицу ковариаций  , если
, если  , и не имеет плотности в
, и не имеет плотности в  .
. имеет многомерное нормальное распределение
имеет многомерное нормальное распределение  . Координаты этого вектора независимы тогда и только тогда, когда они некоррелированы, т.е. когда матрица ковариаций
. Координаты этого вектора независимы тогда и только тогда, когда они некоррелированы, т.е. когда матрица ковариаций 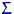 диагональна.
диагональна. квадратичная форма (37) превращается в сумму квадратов
квадратичная форма (37) превращается в сумму квадратов



