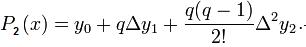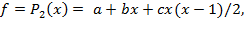Построение модели
Задача о разрезании пиццы
Формулировка задачи: сколько кусков пиццы можно получить, делая n прямолинейных разрезов ножом? Или, каково максимальное число Ln областей, на которые плоскость делится n прямыми?
В качестве примера посмотрим, как можно обнаружить, а потом описать закономерность.
Допустим, что нам нужно решить «Задачу о разрезаниях», то есть надо предсказать, сколько потребуется разрезов в виде прямых линий, чтобы разделить выпуклую фигуру (рис. 1) на заданное (наибольшее) число кусков. Для примера достаточно, чтобы фигура была выпуклой.
Попробуем решить эту задачу вручную.
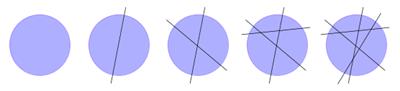
Рис. 1. Задача о разрезании фигуры на заданное число кусков
Из рис. 1 видно, что при 0 разрезах образуется 1 кусок, при 1 разрезе образуется 2 куска, при двух — 4, при трёх — 7, при четырёх — 11. Можете ли вы сейчас сказать наперёд, сколько потребуется разрезов для образования, например, 821 куска? По-моему, нет[1]!
Инженерный подход
Можно провести эксперимент. Как и насколько это продуктивный путь?
В чем затруднение? — Нам неизвестна закономерность y = f (x), где y — количество кусков, x — количество разрезов. Как обнаружить закономерность?
Нам неизвестна функция, но мы знаем ее значения в нескольких точках. Попробуем аппроксимировать неизвестную функцию y = f(x) многочленом (воспользуемся формулой Ньютона). Составим таблицу, связывающую известные нам числа кусков и разрезов.
Таблица 1.
Соответствие разрезов и получающихся фрагментов фигуры
Пока закономерность не ясна. Поэтому рассмотрим разности между отдельными экспериментами, посмотрим, чем отличается результат одного эксперимента от другого. Поняв разницу, мы найдём способ перехода от одного результата к другому, то есть закон, связывающий y и x.
Таблица 2.
Первые разности
| Разрезы
|
|
|
|
|
| …
|
| Куски
|
|
|
|
|
| …
|
| Первые разности
| –
| 1 = 2 – 1
| 2 = 4 – 2
| 3 = 7 – 4
| 4 = 11 – 7
| …
|
Уже кое-какая закономерность проявилась, не правда ли?
Вычислим вторые разности.
Таблица 3.
Вторые разности
| Разрезы
|
|
|
|
|
| …
|
| Куски
|
|
|
|
|
| …
|
| Первые разности
| –
| 1 = 2 – 1
| 2 = 4 – 2
| 3 = 7 – 4
| 4 = 11 – 7
| …
|
| Вторые разности
| –
|
| 1 = 2 – 1
| 1 = 3 – 2
| 1 = 4 – 3
| …
|
Очевидно, что продолжать процедуру вычисления разностей, смысла нет.
Теперь все просто. Функция f называется производящей функцией. Если она линейна, то первые разности равны между собой. Если она квадратичная, то вторые разности равны между собой. И так далее.
Математический подход
Другой подход к решению задачи о разрезании пиццы дает дискретная математика.
Задача о разрезании пиццы
Формулировка задачи: сколько кусков пиццы можно получить, делая n прямолинейных разрезов ножом? Или, каково максимальное число Ln областей, на которые плоскость делится n прямыми?
Снова начнем с рассмотрения крайних случаев.
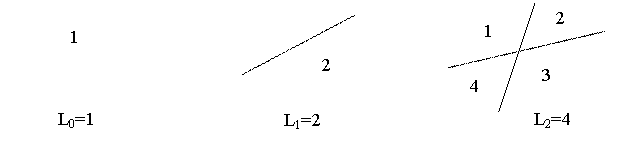
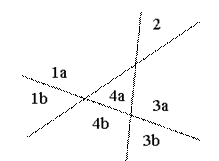
Эксперимент с тремя прямыми показывает, что добавленная третья прямая может рассекать самое большое три старых области вне зависимости от того, как расположены первые две прямые:
Таким образом, L
3=4+3=7 – самое большое, что можно сделать.
Обобщая, приходим к следующему выводу: новая n-я прямая (при n>0) увеличивает число областей на k, когда рассекает k старых областей, то есть когда пересекает прежние прямые в (k−1) различных местах. Две прямые могут пересекаться не более чем в одной точке. Поэтому новая прямая может пересекать (n−1) старых прямых не более чем в (n−1) различных точках, и мы должны иметь k ≤ n. Установлена верхняя граница:
Ln ≤ Ln-1+ n при n>0
В этой формуле можно достичь равенства следующим образом: проводим n-ю прямую так, чтобы она не была параллельна никакой другой прямой (следовательно, она пересекает каждую из них) и так, чтобы она не проходила ни через одну из имеющихся точек пересечения (следовательно, она пересекает каждую из прямых в различных местах). Поэтому рекуррентное соотношение имеет вид:
L0 = 1
Ln = Ln-1+ n при n > 0
Теперь получим решение в замкнутой форме.
Ln = Ln-1+ n = Ln-2+ (n−1) + n = Ln-3+ (n−2) + (n−1) + n = … = L0+1+2+…+(n−2)+(n−1) + n = 1 + 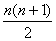
Ln = 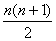 + 1 при n ≥ 0
+ 1 при n ≥ 0
Доказательство методом математической индукции приводится в книге Конкретная математика. Основание информатики. Р. Грэхем, Д. Кнут, О. Паташник Пер. с англ. — М.: Мир, 1998. —703 с.
Отчет о решении задачи
1. Постановка задачи: построить модель, задать вопрос (для заданного количества кусков определить количество разрезов), указать дополнительные условия (для каких y задача имеет решение?).
2. Предложить метод решения задачи в случае квадратного уравнения.
3. Предложить метод решения задачи для замкнутой формы.
4. Написать программы для решения задачи двумя способами. Провести вычисления.
5. Сравнить результаты (по количеству операций)
6. Список литературы.
Аналитический явный способ
Эта модель весьма далека от реальности. Что-либо изучить на ней представляется проблематичным, так как из неё можно найти только время T и место встречи S. Идеализация заключается в том, что дорога считается идеально прямой, без уклонов и подъёмов, скорости объектов считаются постоянными, желания объектов не меняются, силы безграничны, отсутствуют помехи для движения, модель не зависит от величин D, V 1, V 2 (они могут быть сколь угодно большими или малыми).
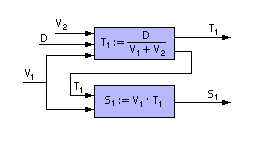
| T1:= D/(V1 + V2) S1:= V1 · T1
| | |
Реальность обычно не имеет ничего общего с такой постановкой задачи. Но за счёт идеализации получается очень простая модель, которая может быть разрешена в общем виде (аналитически) математическими способами. Так формулируются чаще всего алгоритмические модели, где протянута цепочка вычислений от исходных данных к выходу. Поэтому мы применили в записи знак присваивания (:=). После вычисления правой части выражения её значение присваивается переменной, стоящей в левой части. Далее значение этой переменной применено в правой части следующего выражения. Схематически это выглядит так, как показано на рис. 1.18.
|
| Рис. 1.18. Схема решения задачи о встрече (аналитический явный способ)
|
Упражнения.
1. Реализовать программу для проведения вычислений в имитационной алгоритмической постановке задачи.
2. Реализовать программу для проведения вычислений в имитационной статистической постановке задачи.
[1] Я могу ошибаться. Но если знаете, то «это догадка», или вы можете доказать правильность своего утверждения?
Построение модели
Задача о разрезании пиццы
Формулировка задачи: сколько кусков пиццы можно получить, делая n прямолинейных разрезов ножом? Или, каково максимальное число Ln областей, на которые плоскость делится n прямыми?
В качестве примера посмотрим, как можно обнаружить, а потом описать закономерность.
Допустим, что нам нужно решить «Задачу о разрезаниях», то есть надо предсказать, сколько потребуется разрезов в виде прямых линий, чтобы разделить выпуклую фигуру (рис. 1) на заданное (наибольшее) число кусков. Для примера достаточно, чтобы фигура была выпуклой.
Попробуем решить эту задачу вручную.

Рис. 1. Задача о разрезании фигуры на заданное число кусков
Из рис. 1 видно, что при 0 разрезах образуется 1 кусок, при 1 разрезе образуется 2 куска, при двух — 4, при трёх — 7, при четырёх — 11. Можете ли вы сейчас сказать наперёд, сколько потребуется разрезов для образования, например, 821 куска? По-моему, нет[1]!
Инженерный подход
Можно провести эксперимент. Как и насколько это продуктивный путь?
В чем затруднение? — Нам неизвестна закономерность y = f (x), где y — количество кусков, x — количество разрезов. Как обнаружить закономерность?
Нам неизвестна функция, но мы знаем ее значения в нескольких точках. Попробуем аппроксимировать неизвестную функцию y = f(x) многочленом (воспользуемся формулой Ньютона). Составим таблицу, связывающую известные нам числа кусков и разрезов.
Таблица 1.
Соответствие разрезов и получающихся фрагментов фигуры
Пока закономерность не ясна. Поэтому рассмотрим разности между отдельными экспериментами, посмотрим, чем отличается результат одного эксперимента от другого. Поняв разницу, мы найдём способ перехода от одного результата к другому, то есть закон, связывающий y и x.
Таблица 2.
Первые разности
| Разрезы
|
|
|
|
|
| …
|
| Куски
|
|
|
|
|
| …
|
| Первые разности
| –
| 1 = 2 – 1
| 2 = 4 – 2
| 3 = 7 – 4
| 4 = 11 – 7
| …
|
Уже кое-какая закономерность проявилась, не правда ли?
Вычислим вторые разности.
Таблица 3.
Вторые разности
| Разрезы
|
|
|
|
|
| …
|
| Куски
|
|
|
|
|
| …
|
| Первые разности
| –
| 1 = 2 – 1
| 2 = 4 – 2
| 3 = 7 – 4
| 4 = 11 – 7
| …
|
| Вторые разности
| –
|
| 1 = 2 – 1
| 1 = 3 – 2
| 1 = 4 – 3
| …
|
Очевидно, что продолжать процедуру вычисления разностей, смысла нет.
Теперь все просто. Функция f называется производящей функцией. Если она линейна, то первые разности равны между собой. Если она квадратичная, то вторые разности равны между собой. И так далее.
Прямая интерполяционная формула Ньютона
или первая интерполяционная формула Ньютона, применяется для интерполирования вперёд: 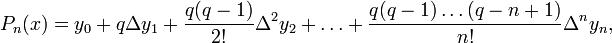 где
где 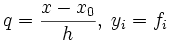 , а выражения вида
, а выражения вида 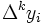 — конечные разности.
— конечные разности.
Функция f есть частный случай формулы Ньютона:
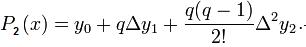
Выразим через x (h = 1):
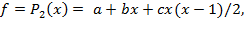
где a = y0, b = Δy1, c = Δ2y2.
Коэффициенты a, b, c для нашей квадратичной функции f находятся в первых ячейках строк экспериментальной таблицы 4.
Таблица 4.
Коэффициенты производящей функции
| Разрезы
|
|
|
|
|
| …
|
| Куски
| y0 =1
|
|
|
|
| …
|
| Первые разности
| –
| Δy1 = 1
| 2 = 4 – 2
| 3 = 7 – 4
| 4 = 11 – 7
| …
|
| Вторые разности
| –
|
| Δ2y2 = 1
| 1 = 3 – 2
| 1 = 4 – 3
| …
|
Итак, закономерность есть, и она такова:
f = a + b · x + c · x · (x – 1)/2 = 1 + x + x · (x – 1)/2 = 0.5 · x 2 + 0.5 · x + 1.
Теперь, когда закономерность определена, можно решить обратную задачу и ответить на поставленный вопрос: сколько надо выполнить разрезов, чтобы получить 821 кусок? x =?
Решаем квадратное уравнение 821 = 0.5 · x 2 + 0.5 · x + 1, находим корни: x = 41.
Упражнение. Написать программу решения квадратного уравнения. Ответить на вопрос, для каких y имеет решение уравнение y = 0.5 · x 2 + 0.5 · x + 1?
Подведём итоги (обратите на это внимание!).
Сразу угадать решение мы не смогли. Поставить эксперимент оказалось затруднительно. Пришлось построить модель, то есть найти закономерность между переменными. Модель получилась в виде уравнения. Добавив к модели вопрос и уравнение, отражающее известное условие, образовали задачу. Поскольку задача оказалась типового вида (канонического), то её удалось решить известным методом.
Математический подход
Другой подход к решению задачи о разрезании пиццы дает дискретная математика.
Задача о разрезании пиццы
Формулировка задачи: сколько кусков пиццы можно получить, делая n прямолинейных разрезов ножом? Или, каково максимальное число Ln областей, на которые плоскость делится n прямыми?
Снова начнем с рассмотрения крайних случаев.

Эксперимент с тремя прямыми показывает, что добавленная третья прямая может рассекать самое большое три старых области вне зависимости от того, как расположены первые две прямые:
Таким образом, L
3=4+3=7 – самое большое, что можно сделать.
Обобщая, приходим к следующему выводу: новая n-я прямая (при n>0) увеличивает число областей на k, когда рассекает k старых областей, то есть когда пересекает прежние прямые в (k−1) различных местах. Две прямые могут пересекаться не более чем в одной точке. Поэтому новая прямая может пересекать (n−1) старых прямых не более чем в (n−1) различных точках, и мы должны иметь k ≤ n. Установлена верхняя граница:
Ln ≤ Ln-1+ n при n>0
В этой формуле можно достичь равенства следующим образом: проводим n-ю прямую так, чтобы она не была параллельна никакой другой прямой (следовательно, она пересекает каждую из них) и так, чтобы она не проходила ни через одну из имеющихся точек пересечения (следовательно, она пересекает каждую из прямых в различных местах). Поэтому рекуррентное соотношение имеет вид:
L0 = 1
Ln = Ln-1+ n при n > 0
Теперь получим решение в замкнутой форме.
Ln = Ln-1+ n = Ln-2+ (n−1) + n = Ln-3+ (n−2) + (n−1) + n = … = L0+1+2+…+(n−2)+(n−1) + n = 1 + 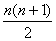
Ln = 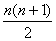 + 1 при n ≥ 0
+ 1 при n ≥ 0
Доказательство методом математической индукции приводится в книге Конкретная математика. Основание информатики. Р. Грэхем, Д. Кнут, О. Паташник Пер. с англ. — М.: Мир, 1998. —703 с.
Отчет о решении задачи
1. Постановка задачи: построить модель, задать вопрос (для заданного количества кусков определить количество разрезов), указать дополнительные условия (для каких y задача имеет решение?).
2. Предложить метод решения задачи в случае квадратного уравнения.
3. Предложить метод решения задачи для замкнутой формы.
4. Написать программы для решения задачи двумя способами. Провести вычисления.
5. Сравнить результаты (по количеству операций)
6. Список литературы.





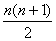
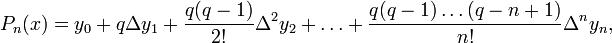 где
где 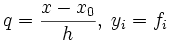 , а выражения вида
, а выражения вида 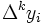 — конечные разности.
— конечные разности.