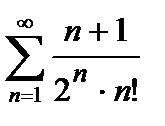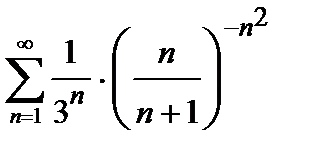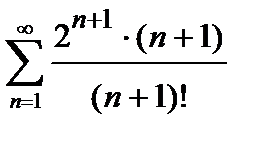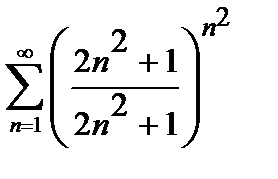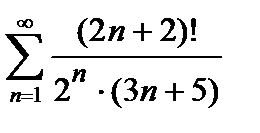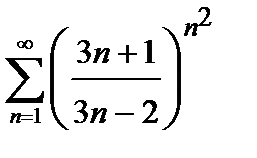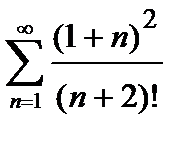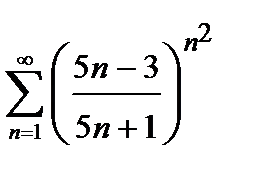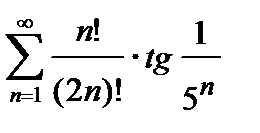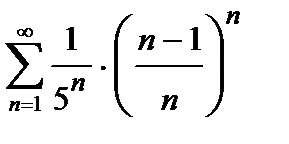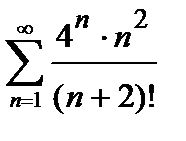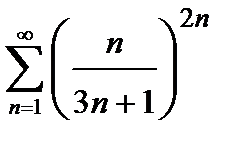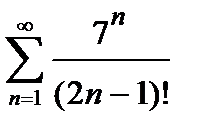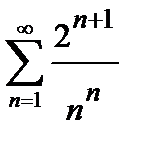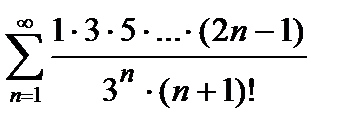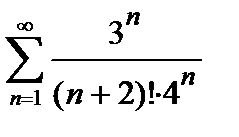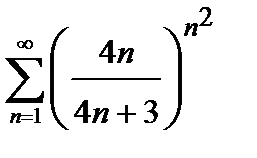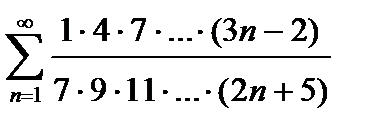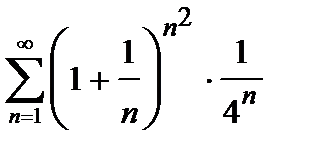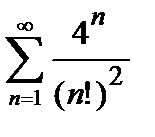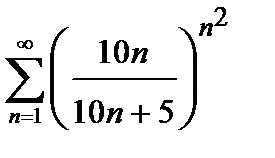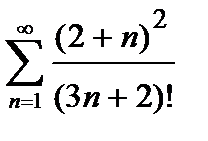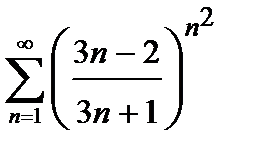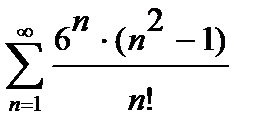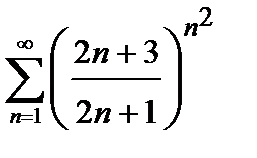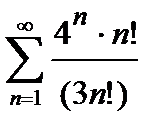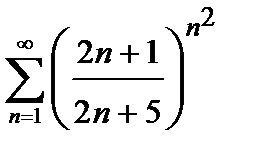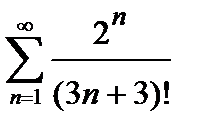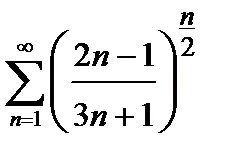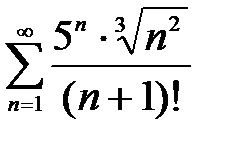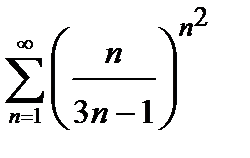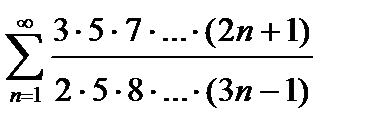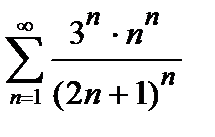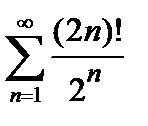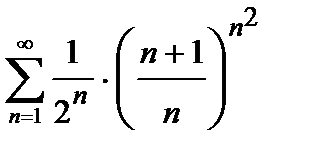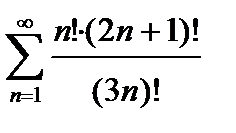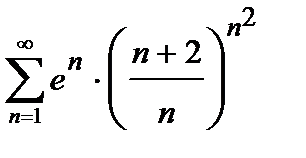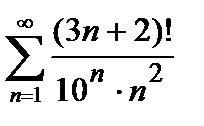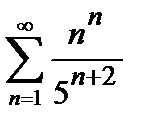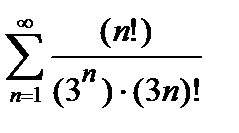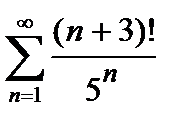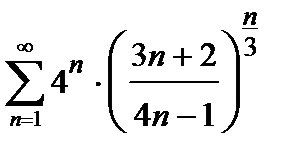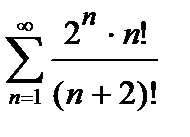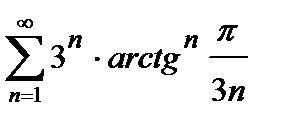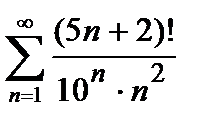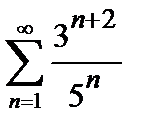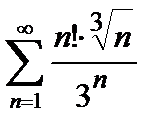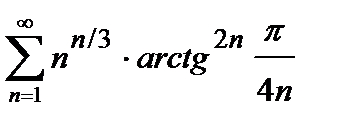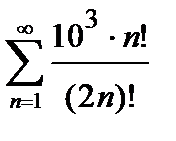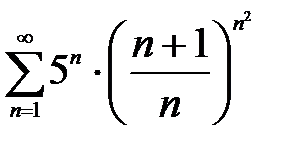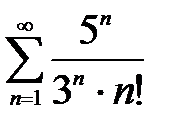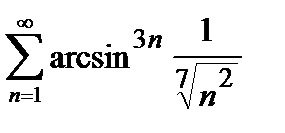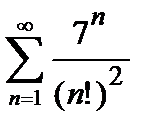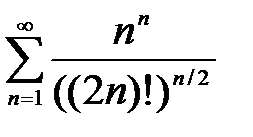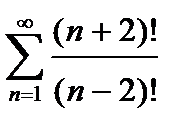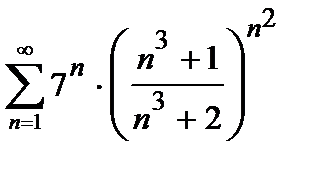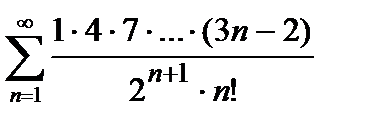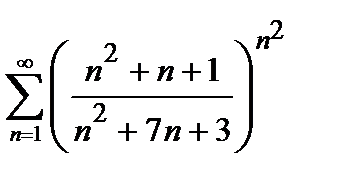Основные понятия
1. Общим решением дифференциального уравненияпервого порядка называется дифференцируемая функция y =  (х, С), которая при любом значении произвольной постоянной С является решением данного уравнения. Решения, получающиеся из общего решения y =
(х, С), которая при любом значении произвольной постоянной С является решением данного уравнения. Решения, получающиеся из общего решения y = 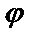 (х, С) при определенном значении произвольной постоянной С, называются частными. Задача нахождения частного решения, удовлетворяющего начальным условиям y=
(х, С) при определенном значении произвольной постоянной С, называются частными. Задача нахождения частного решения, удовлетворяющего начальным условиям y=  при
при 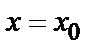 (другая запись
(другая запись 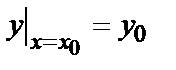 ), называется задачей Коши.
), называется задачей Коши.
График всякого решения y = 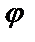 (х) данного дифференциального уравнения, построенный на плоскости хОy, называется интегральной кривой этого уравнения.
(х) данного дифференциального уравнения, построенный на плоскости хОy, называется интегральной кривой этого уравнения.
8.2. Дифференциальные уравнения с разделяющимися переменными. Наиболее простым дифференциальным уравнением первого порядка является уравнение вида:
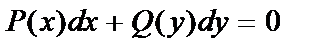 , (1)
, (1)
где P (x) зависит только от х, а Q (y) - от у.
Проинтегрировав почленно это уравнение, получаем:
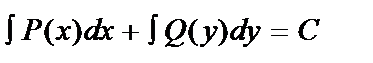 - его общий интеграл.
- его общий интеграл.
8.3. Однородные дифференциальные уравнения первого порядка приводятся к уравнению с разделяющимися переменными.
Функция f (x; y) называется однородной функцией n -го порядка (измерения), если при умножении каждого ее аргумента на произвольный множитель 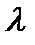 вся функция умножится на
вся функция умножится на 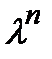 , то есть:
, то есть: 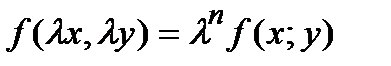 .
.
Например, 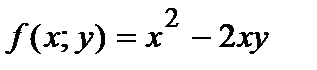 - однородная функция второго порядка, так как
- однородная функция второго порядка, так как 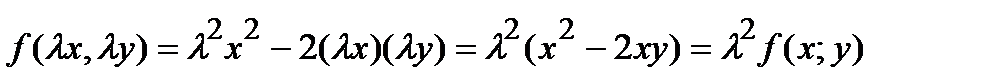 .
.
Дифференциальное уравнение
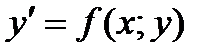 (2)
(2)
называется однородным, если функция 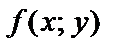 однородного нулевого порядка.
однородного нулевого порядка.
Если 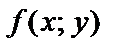 однородная функция нулевого порядка, то по определению
однородная функция нулевого порядка, то по определению 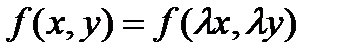 . Положив
. Положив 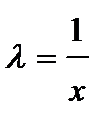 , получаем:
, получаем: 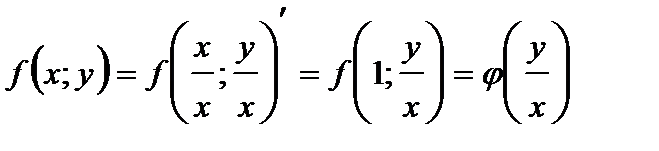 .
.
Дифференциальное уравнение (2) можно записать в виде:
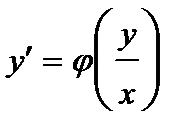 (3)
(3)
Однородное дифференциальное уравнение (3) преобразуется в уравнение с разделяющимися переменными при помощи замены переменной (подстановки): 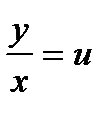 или
или 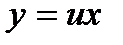 .
.
Подставив 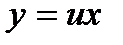 и
и 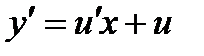 в уравнение (3) получаем:
в уравнение (3) получаем:
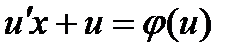 или
или 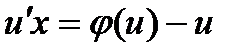 ,
,
то есть уравнение с разделяющимися переменными. Найдя его общее решение (общий интеграл), следует заменить в нем 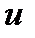 на
на 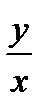 . Получим общее решение (интеграл) исходного уравнения.
. Получим общее решение (интеграл) исходного уравнения.
8.4. Линейные дифференциальные уравнения. Дифференциальное уравнение первого порядка называется линейным, если оно имеет вид:
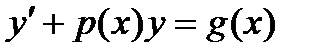 (4)
(4)
где 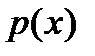 и
и 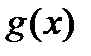 - некоторые (непрерывные) функции переменной х. В случае, когда
- некоторые (непрерывные) функции переменной х. В случае, когда 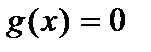 , уравнение называетсяоднородным; если
, уравнение называетсяоднородным; если 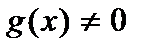
 неоднородным.
неоднородным.
Общее решение дифференциального уравнения (4) будем искать в виде: 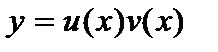 . Так как
. Так как 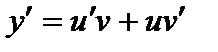 , то подставив в уравнение (4), получим:
, то подставив в уравнение (4), получим:
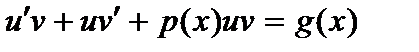 или
или 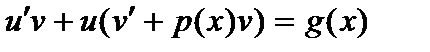 .
.
Сначала находят частное решение 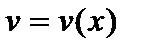 уравнения
уравнения 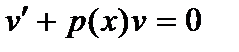 , тогда функция
, тогда функция 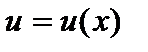 - решение уравнения
- решение уравнения 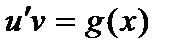 . Учитывая, что
. Учитывая, что 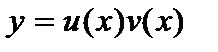 , получим общее решение линейного дифференциального уравнения (4).
, получим общее решение линейного дифференциального уравнения (4).
8.5. Дифференциальное уравнение n – го порядка, разрешенное относительно производной, имеет вид 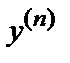 = f (х, у, у′,…,
= f (х, у, у′,…, 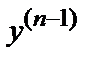 ).
).
Задача нахождения решения у = 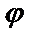 (х) данного уравнения, удовлетворяющего начальным условиям
(х) данного уравнения, удовлетворяющего начальным условиям 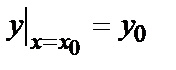 ;
; 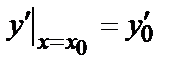 ;
; 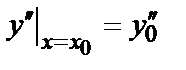 ; …;
; …; 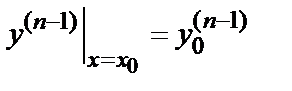 , называется задачей Коши.
, называется задачей Коши.
Для нахождения частного решения иногда используют так называемые краевые условия. Эти условия (их число не должно превышать порядка уравнения) задаются не в одной точке, а на концах некоторого промежутка. Краевые условия ставятся лишь для уравнений порядка выше первого.
Теорема существования и единственности решения задачи Коши. Если в уравнении 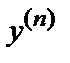 = f (х, у, у ′, …,
= f (х, у, у ′, …, 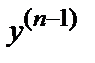 ) функция f (х, у, у ′,…,
) функция f (х, у, у ′,…, 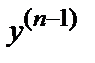 ):
):
a) непрерывна по всем своим аргументам х, у, у ′, …, 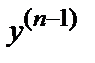 в некоторой области D их изменения;
в некоторой области D их изменения;
б) имеет ограниченные в области D частные производные 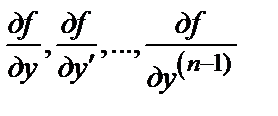 по аргументам у, у ′, …
по аргументам у, у ′, … 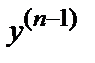 , то найдется интервал
, то найдется интервал 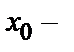 h < х <
h < х < 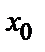 + h (h > 0), на котором существует единственное решение у =
+ h (h > 0), на котором существует единственное решение у = 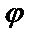 (х) данного уравнения, удовлетворяющее условиям у (
(х) данного уравнения, удовлетворяющее условиям у (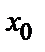 )=
)= 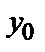 ; у ′(
; у ′(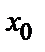 )=
)= 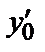 ; …;
; …; 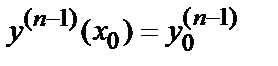 , где значения х =
, где значения х = 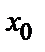 ; у =
; у = 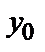 ; у ′=
; у ′= 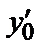 ; …;
; …; 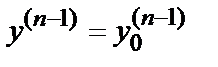 содержатся в области D.
содержатся в области D.
Проинтегрировать (в конечном виде) уравнение n– го порядка можно только в некоторых частных случаях.
8.6. Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид 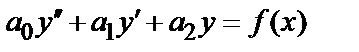 , где
, где 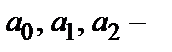 числа, причем
числа, причем 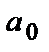 ≠0. Если f (х) = 0, то уравнение называется однородным, а если f(х)≠ 0 – неоднородным.
≠0. Если f (х) = 0, то уравнение называется однородным, а если f(х)≠ 0 – неоднородным.
Квадратное уравнение 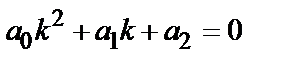 называется характеристическим уравнением дифференциального уравнения
называется характеристическим уравнением дифференциального уравнения 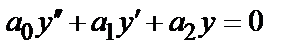 . Пусть D =
. Пусть D = 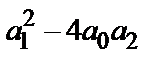 дискриминант квадратного уравнения. Возможны следующие случаи:
дискриминант квадратного уравнения. Возможны следующие случаи:
1) D >0 – общим решением уравнения 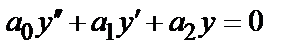 является функция
является функция 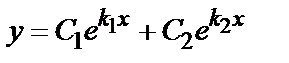 (
(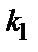 и
и 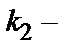 корни характеристического уравнения);
корни характеристического уравнения);
2) D =0 – общим решением служит функция у = 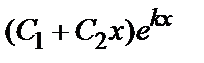 (k –корень характеристического уравнения);
(k –корень характеристического уравнения);
3) D <0–общим решением является функция 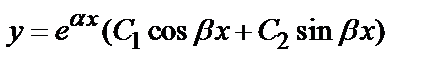 (
(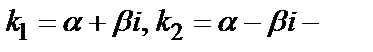 корни характеристического уравнения).
корни характеристического уравнения).
Решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами основывается на следующей теореме.
Теорема. Если 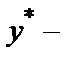 некоторое частное решение неоднородного уравнения
некоторое частное решение неоднородного уравнения 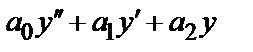 = f (х)и Y –общее решение соответствующего однородного уравнения
= f (х)и Y –общее решение соответствующего однородного уравнения 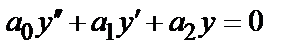 , то общее решение неоднородного уравнения имеет вид у = Y + у *.
, то общее решение неоднородного уравнения имеет вид у = Y + у *.
Укажем правило нахождения частного решения неоднородного уравнения методом неопределенных коэффициентов.
1) Пусть f (х)= 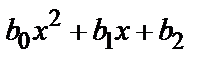 ; тогда:
; тогда:
а) у *= 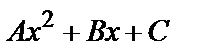 , если нуль не является корнем характеристического уравнения;
, если нуль не является корнем характеристического уравнения;
б) у *= 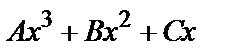 , если нуль является простым корнем характеристического уравнения;
, если нуль является простым корнем характеристического уравнения;
в) у *= 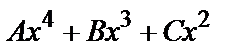 , если нуль является двукратным корнем характеристического уравнения.
, если нуль является двукратным корнем характеристического уравнения.
2) Пусть f (х)= 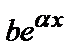 ; тогда:
; тогда:
а) у *= 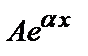 , если число
, если число 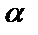 не является корнем характеристического уравнения;
не является корнем характеристического уравнения;
б) у *= 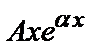 , если число
, если число 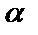 является корнем характеристического уравнения;
является корнем характеристического уравнения;
в) у *= 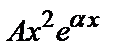 , если число
, если число 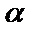 является двукратным корнем характеристического уравнения.
является двукратным корнем характеристического уравнения.
3) Пусть f (х)= 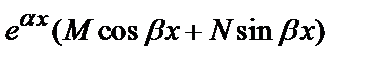 ; тогда:
; тогда:
а) у *= 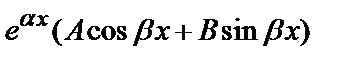 , если число
, если число 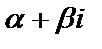 не является корнем характеристического уравнения;
не является корнем характеристического уравнения;
б) у *= 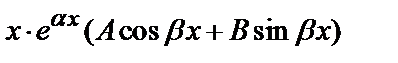 , если число
, если число 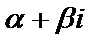 является корнем характеристического уравнения.
является корнем характеристического уравнения.
8.7. Решение типового задания
Пример 1. Найти общее решение уравнения 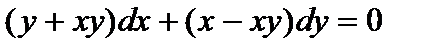 .
.
Решение. Выносим общий множитель из первой и второй скобки:
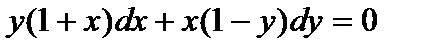 .
.
Получаем уравнение с разделяющимися переменными, разделив его на 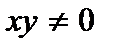 , получим
, получим
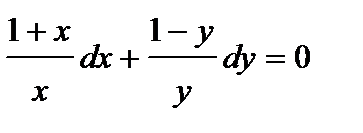 .
.
Интегрируя последнее уравнение, получаем:
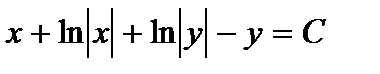 или
или 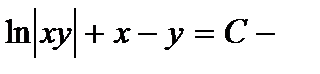 общий интеграл
общий интеграл
Пример 2. Найти общее решение уравнения 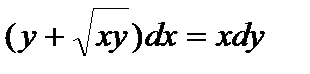 .
.
Решение. Функции P и Q – однородные функции первого порядка.
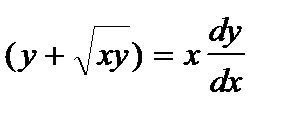 или
или 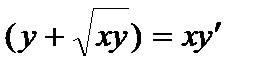 .
.
Положим 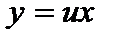 , тогда
, тогда 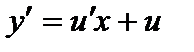 . Подставляя в последнее уравнение, получаем:
. Подставляя в последнее уравнение, получаем:
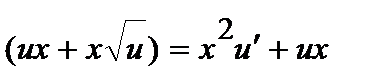 или
или 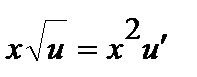 .
.
Учитывая, что 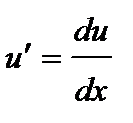 , получаем
, получаем 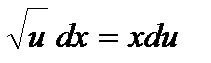 или
или 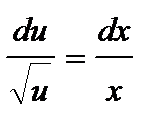 . Интегрируя почленно это уравнение, имеем:
. Интегрируя почленно это уравнение, имеем:
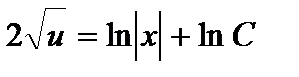 .
.
Возвращаясь к старой переменной, получаем общее решение:
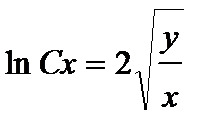 или
или 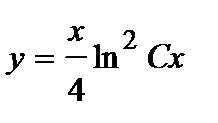 .
.
Пример 3. Найти общее решение уравнения 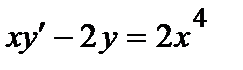 .
.
Решение. Разделив левую и правую части на х, приходим к линейному неоднородному уравнению:
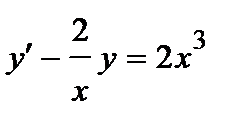 .
.
Пусть 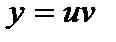 , тогда
, тогда 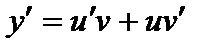 . Подставляя в последнее уравнение, получаем:
. Подставляя в последнее уравнение, получаем:
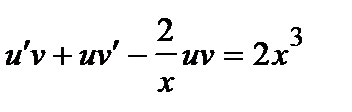 или
или 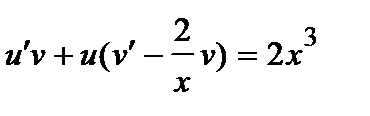 .
.
Положим 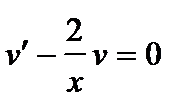 или
или 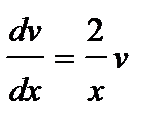 , откуда
, откуда 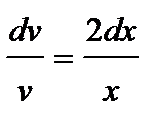 . Проинтегрировав, найдем какое-либо частное решение этого уравнения, например, при С =0 имеем
. Проинтегрировав, найдем какое-либо частное решение этого уравнения, например, при С =0 имеем 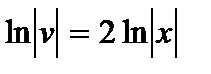 и
и 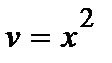 .
.
Найденное значение 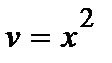 подставляем в уравнение
подставляем в уравнение 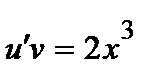 или
или 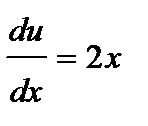 .
.
Решая это уравнение с разделяющимися переменными, получаем 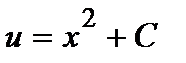 . Тогда окончательно имеем
. Тогда окончательно имеем 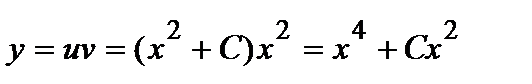 .
.
Пример 4. Найти общее решение уравнения 2 ху ′′′= у ′′ и частное решение, удовлетворяющее начальным условиям у (1)= 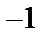 ; у ′(1)=0; у ′′(1)=1.
; у ′(1)=0; у ′′(1)=1.
Решение. Пусть у ′′= z. Имеем 2 хz ′ 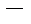 z =0
z =0 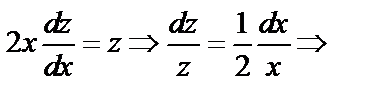
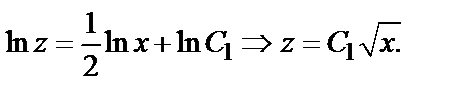
Но z = у ′′ 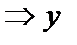 ′′=
′′= 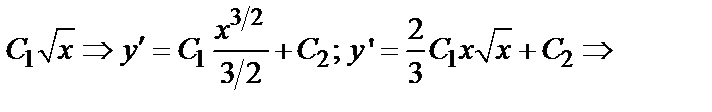
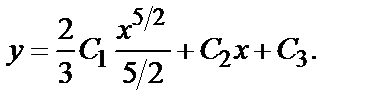 Следовательно, у =
Следовательно, у = 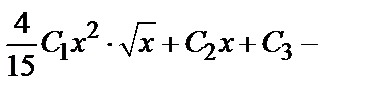 общее решение дифференциального уравнения.
общее решение дифференциального уравнения.
Чтобы найти частное решение, подставим в выражения для у, у ′ и у ′′ значение х =1:
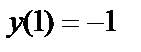
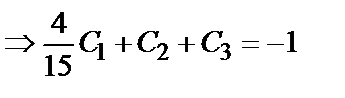 ;
;
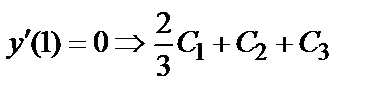 =0;
=0;
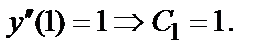
Из системы уравнений 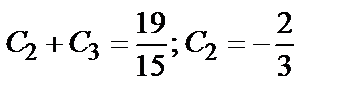 находим
находим 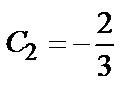 ;
; 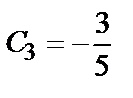 . Значит, искомое частное решение имеет вид:
. Значит, искомое частное решение имеет вид:
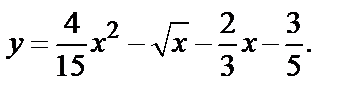
Пример 5. Найти общее решение уравнения y ′′ 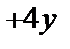 ′+13 у =5sin2 х и частное решение, удовлетворяющее начальным условиям
′+13 у =5sin2 х и частное решение, удовлетворяющее начальным условиям 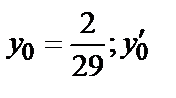 =
= 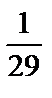 при х =0.
при х =0.
Решение. Рассмотрим однородное уравнение y ′′ 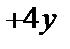 ′+13 у =0. Соответствующее характеристическое уравнение имеет вид
′+13 у =0. Соответствующее характеристическое уравнение имеет вид 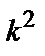 +4 k +13=0, откуда
+4 k +13=0, откуда 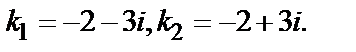 Следовательно, Y =
Следовательно, Y = 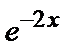
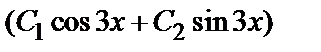 общее решение однородного уравнения.
общее решение однородного уравнения.
Частное решение неоднородного уравнения будем искать в виде
у *= 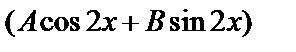 . Имеем:
. Имеем:
(у *)′= 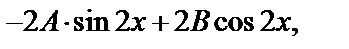 (у *)′′=
(у *)′′= 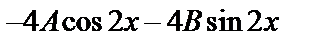 .
.
Подставим эти выражения в неоднородное уравнение
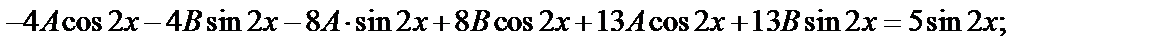
(9 А +8 В)cos2 х +(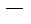 8 А +9 В)sin2 х =5sin2 х
8 А +9 В)sin2 х =5sin2 х
и получим систему для вычисления коэффициентов А и В:
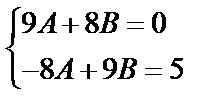
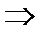
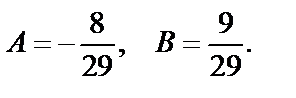
Итак, частное решение неоднородного уравнения имеет вид:
у *= 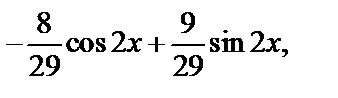
а общее решение неоднородного уравнения – вид
у = 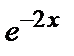
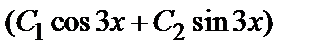
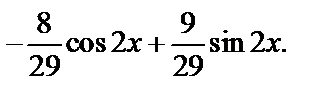
Найдем частное решение, удовлетворяющее заданным начальным условиям:
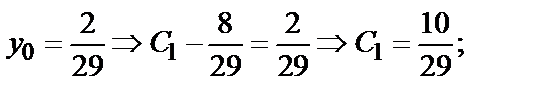
y= 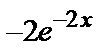
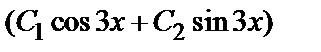 +
+ 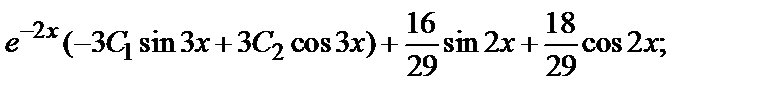
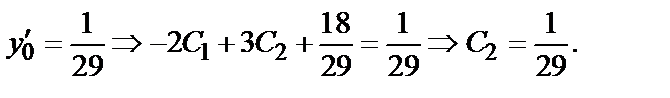
Искомое частное решение таково:
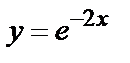
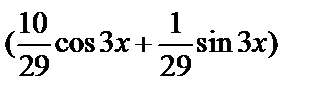
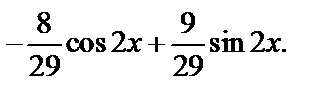
Задачи 361-390:
Найти общее решение дифференциальных уравнений.
361. а) 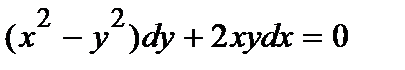
| б) 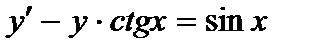
|
362. а) 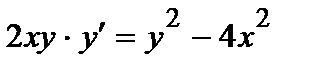
| б) 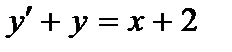
|
363. а) 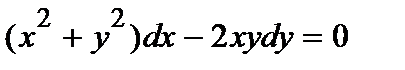
| б) 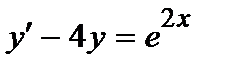
|
364. а) 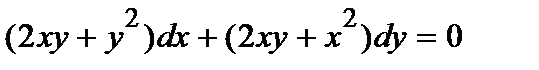
| б) 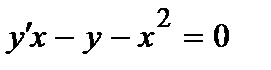
|
365. а) 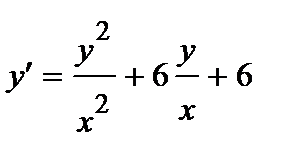
| б) 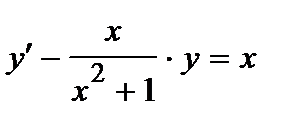
|
366. а) 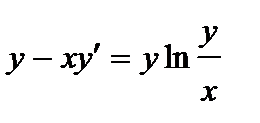
| б) 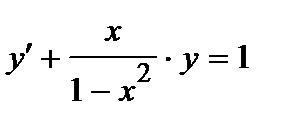
|
367. а) 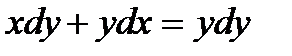
| б) 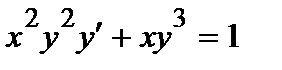
|
368. а) 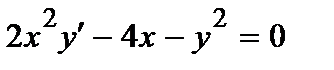
| б) 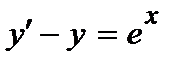
|
369. а) 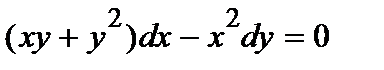
| б) 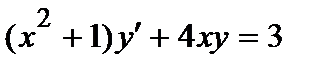
|
370. а) 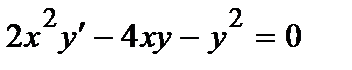
| б) 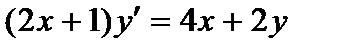
|
371. а) 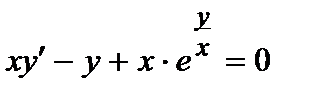
| б) 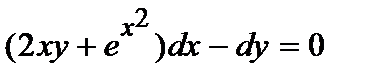
|
372. а) 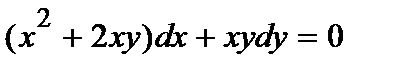
| б) 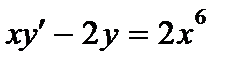
|
373. а) 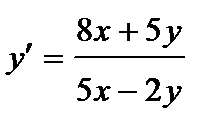
| б) 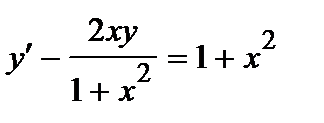
|
374. а) 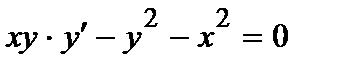
| б) 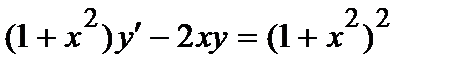
|
375. а) 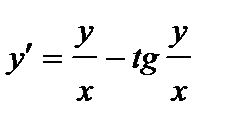
| б) 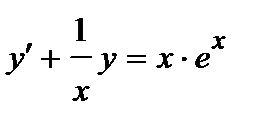
|
376. а) 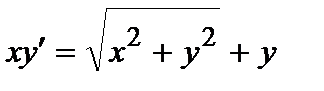
| б) 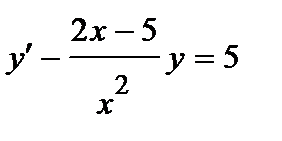
|
377. а) 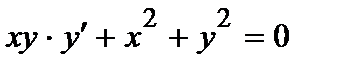
| б) 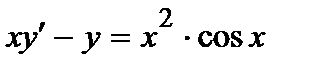
|
378. а) 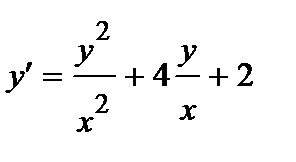
| б) 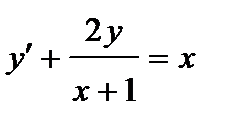
|
379. а) 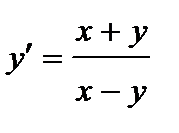
| б) 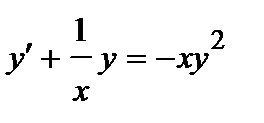
|
380. а) 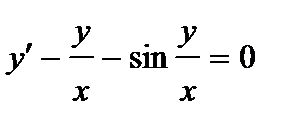
| б) 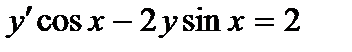
|
381. a) 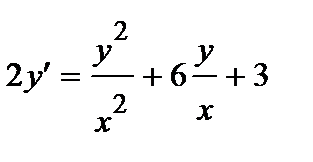
| б) 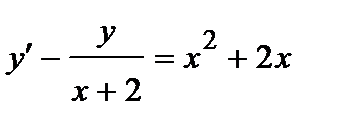
|
382. a) 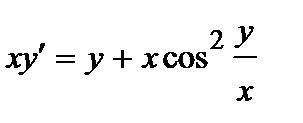
| б) 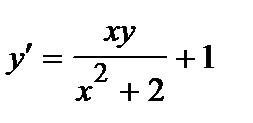
|
383. a) 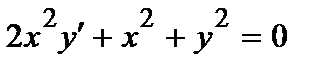
| б) 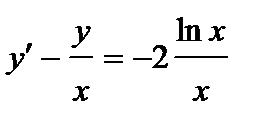
|
384. a) 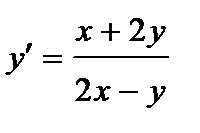
| б) 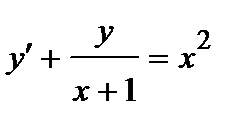
|
385. a) 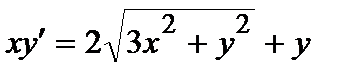
| б) 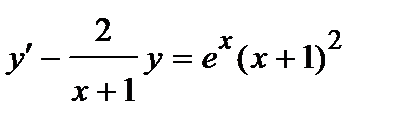
|
386. a) 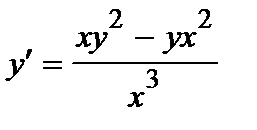
| б) 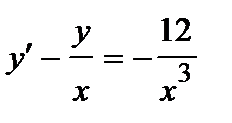
|
387. a) 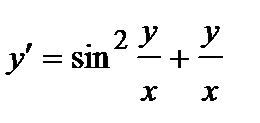
| б) 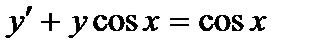
|
388. a) 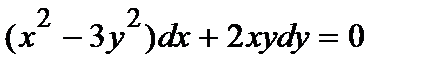
| б) 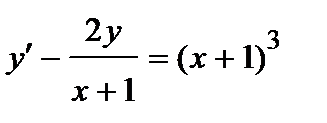
|
389. a) 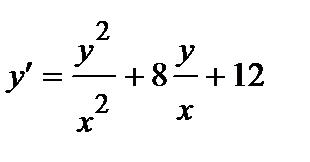
| б) 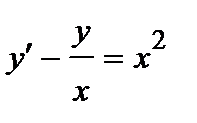
|
390. a) 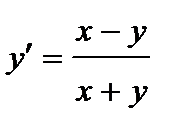
| б) 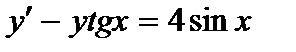
|
Задачи №391-420:
Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальным условиям.
391. 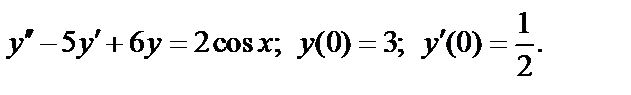
392. 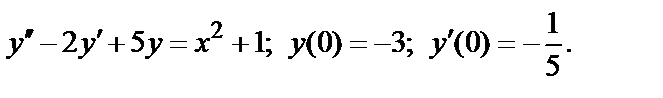
393. 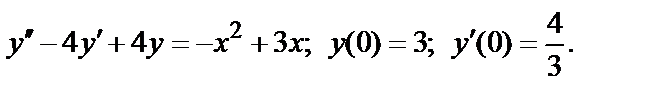
394. 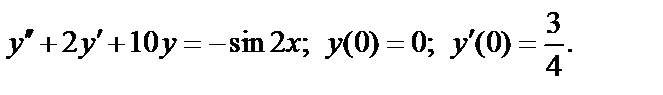
395. 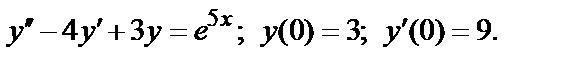
396. 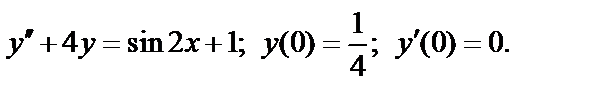
397. 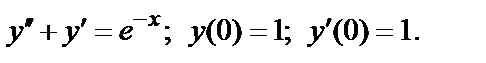
398. 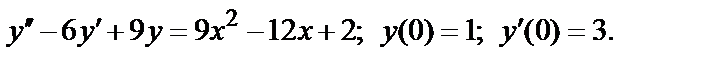
399. 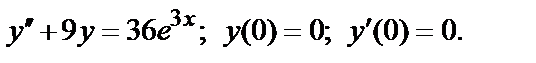
400. 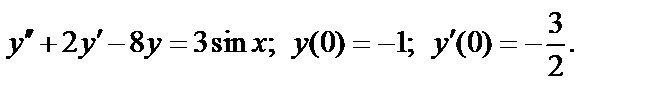
401. 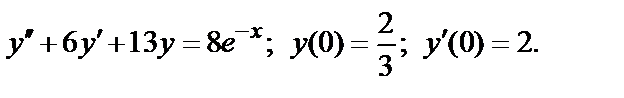
402. 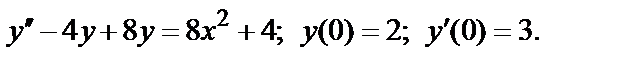
403. 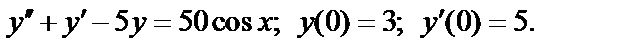
404. 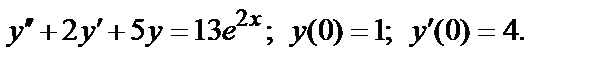
405. 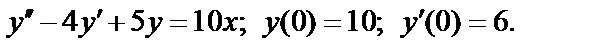
406. 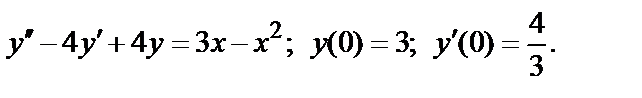
407. 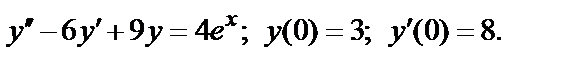
408. 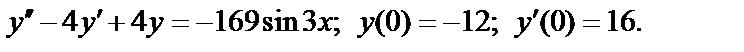
409. 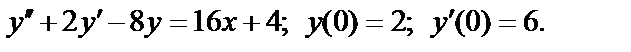
410. 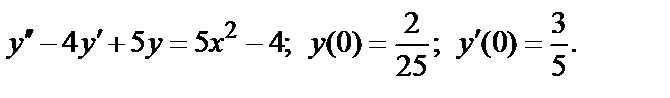
411. 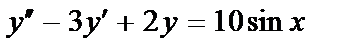 ;
; 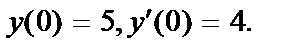
412. 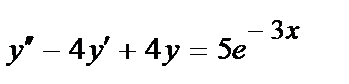 ;
; 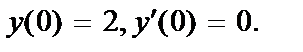
413. 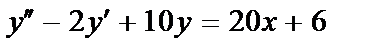 ;
; 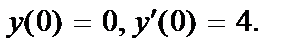
414. 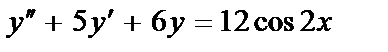 ;
; 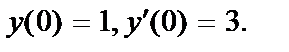
415. 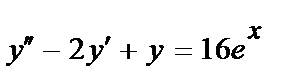 ;
; 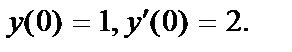
416. 23. 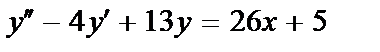 ;
; 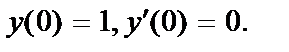
417. 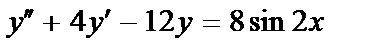 ;
; 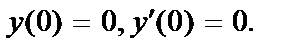
418. 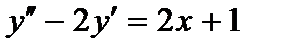 ;
; 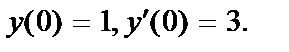
419. 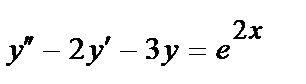 ;
; 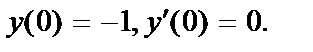
420. 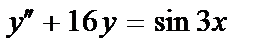 ;
; 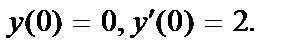
Тема 9. Ряды
Числовой ряд. Основные понятия
Числовой ряд 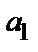 +
+ 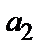 +…+ а
+…+ а 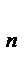 +… =
+… = 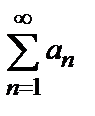 , (1)
, (1)
называется сходящимися, если существует предел его частичных сумм 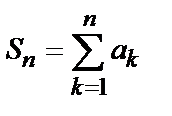 . Число
. Число 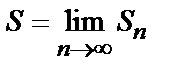 называется суммой ряда. Если же предел частичных сумм не существует, то ряд (1) называется расходящимися.
называется суммой ряда. Если же предел частичных сумм не существует, то ряд (1) называется расходящимися.
Необходимый признак сходимости: если ряд (1) сходится, то его общий член стремится к нулю при 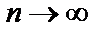 :
: 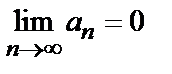 .
.
К достаточным признакам сходимости рядов с положительными членами (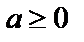 ) относятся:
) относятся:
9.2. Признак сравнения в предельной форме: если
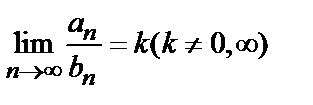 , (2)
, (2)
то ряды 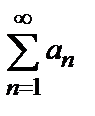 и
и 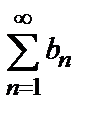 одновременно сходится или расходится. В качестве эталонных рядов для сравнения обычно служат:
одновременно сходится или расходится. В качестве эталонных рядов для сравнения обычно служат:
ряд 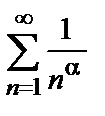 сходящийся при
сходящийся при 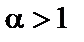 и расходящийся при
и расходящийся при 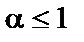 ;
;
ряд 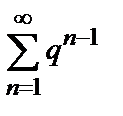 , сходящийся при
, сходящийся при 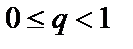 и расходящийся
и расходящийся 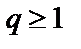 .
.
9.3. Признак Даламбера: если существует
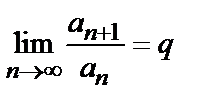 , (3)
, (3)
то ряд 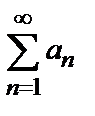 сходится при
сходится при 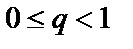 и расходится при
и расходится при 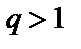 . Если же
. Если же 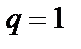 , то вопрос о сходимости ряда этим признаком не решается.
, то вопрос о сходимости ряда этим признаком не решается.
Ряд 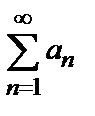 с членами, имеющими разные знаки, называется условно сходящимся, если ряд
с членами, имеющими разные знаки, называется условно сходящимся, если ряд 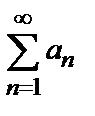 сходится, а ряд
сходится, а ряд 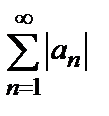 расходится, и абсолютно сходящимся, если ряд
расходится, и абсолютно сходящимся, если ряд 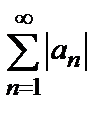 сходится.
сходится.
9.4. Радикальный признак Коши: если для ряда 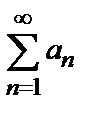 существует
существует
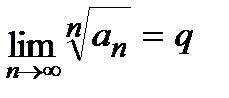 , (4)
, (4)
то ряд сходится при 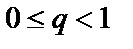 и расходится при
и расходится при 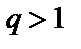 . Если же
. Если же 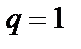 , то вопрос о сходимости ряда этим признаком не решается.
, то вопрос о сходимости ряда этим признаком не решается.
9.5. Признак Лейбница: если члены ряда 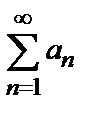 удовлетворяют условиям:
удовлетворяют условиям:
1) 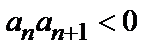 (т.е. ряд знакочередующийся);
(т.е. ряд знакочередующийся);
2) 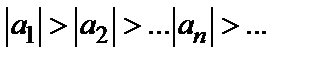 ;
;
3) 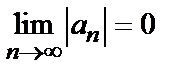 , то ряд сходится. Погрешность
, то ряд сходится. Погрешность  , происходящая от замены суммы сходящегося знакочередующегося ряда суммой его первых n членов, по абсолютной величине меньше первого из отброшенных членов:
, происходящая от замены суммы сходящегося знакочередующегося ряда суммой его первых n членов, по абсолютной величине меньше первого из отброшенных членов:
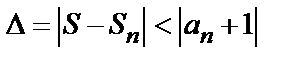 . (5)
. (5)
9.6. Степенной ряд. Ряд вида
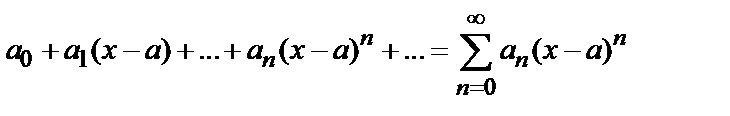 (6)
(6)
называется степенным рядом [относительно 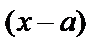 ], точка
], точка 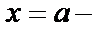 центром разложения,
центром разложения, 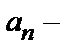 коэффициентами ряда. Число
коэффициентами ряда. Число 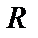 называется радиусом сходимости степенного ряда, если ряд (6) сходится при
называется радиусом сходимости степенного ряда, если ряд (6) сходится при 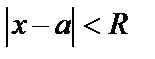 и расходится при
и расходится при 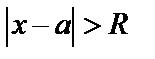 . При
. При 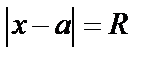 ряд может как сходится, так и расходится. Интервал
ряд может как сходится, так и расходится. Интервал 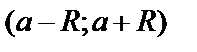 называется интервалом сходимости степенного ряда (6). Радиус сходимости R может быть найден по формуле
называется интервалом сходимости степенного ряда (6). Радиус сходимости R может быть найден по формуле
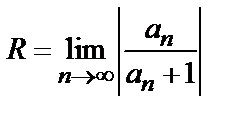 . (7)
. (7)
Степенной ряд (6) внутри интервала сходимости можно почленно дифференцировать и интегрировать с сохранением радиуса сходимости.
9.7. Решение типового задания
Пример 1. Исследовать на сходимость числовой ряд 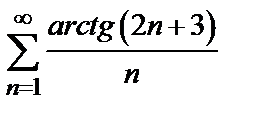 .
.
Решение. Проверяем сходимость ряда по признаку Даламбера (3). Так как общий член ряда 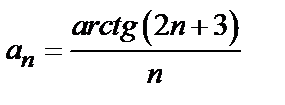 , то, заменяя в выражении n- го члена n на n +1, находим
, то, заменяя в выражении n- го члена n на n +1, находим 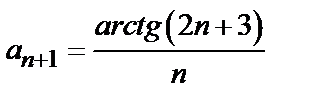 . Затем ищем предел отношения последующего члена
. Затем ищем предел отношения последующего члена 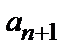 к предыдущему
к предыдущему 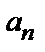 при
при 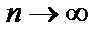 :
:
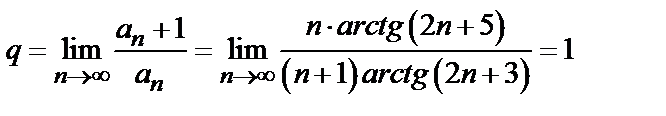 .
.
Поскольку полученный предел равен единице, признак Даламбера не дает ответа на вопрос о сходимости ряда (здесь для вычисления предела было использовано правило Лопиталя). Применим теперь признак сравнения в предельной форме. В качестве эталонного ряда выберем ряд 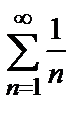 ,
, 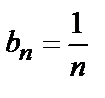 и в силу формулы (2) получим
и в силу формулы (2) получим
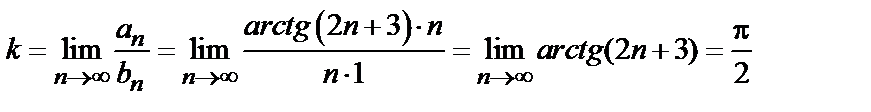 .
.
Следовательно, исследуемый ряд является расходящимся, так как эталонный ряд с общим членом  расходится (гармонический ряд).
расходится (гармонический ряд).
Пример 2. Исследовать на сходимость числовой ряд 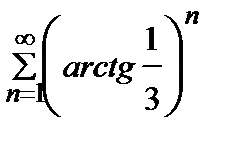 .
.
Решение. Проверяем сходимость ряда по радикальному признаку Коши (4).
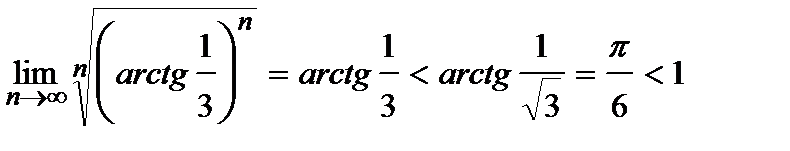
– ряд сходится.
Пример 3. Исследовать на сходимость числовой ряд 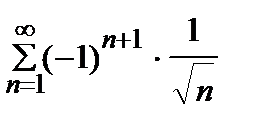 .
.
Решение. Проверяем сходимость ряда по признаку Лейбница (4).
1) 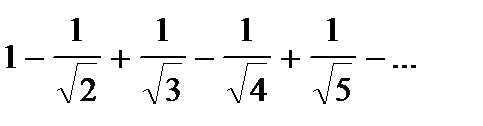 (т.е. ряд знакочередующийся);
(т.е. ряд знакочередующийся);
2) 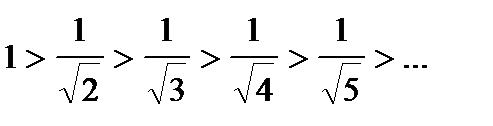 (монотонно убывают);
(монотонно убывают);
3) 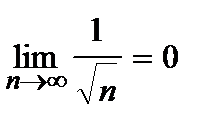 , то ряд сходится.
, то ряд сходится.
Ряд из абсолютных величин членов ряда 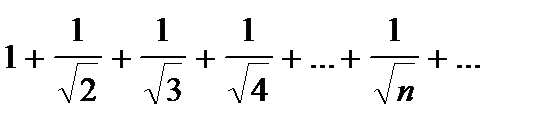 , общий член которого имеет вид
, общий член которого имеет вид 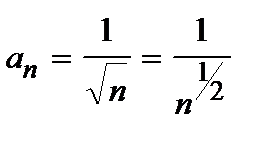 . Обобщенный гармонический ряд
. Обобщенный гармонический ряд 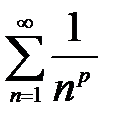 при p <1 расходится. Таким образом, исследуемый ряд сходится условно.
при p <1 расходится. Таким образом, исследуемый ряд сходится условно.
Пример 4. Найти радиус и интервал сходимости степенного ряда 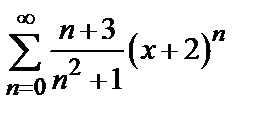 . Исследовать сходимость ряда на концах интервала сходимости.
. Исследовать сходимость ряда на концах интервала сходимости.
Решение. Радиус сходимости находим по формуле (7):
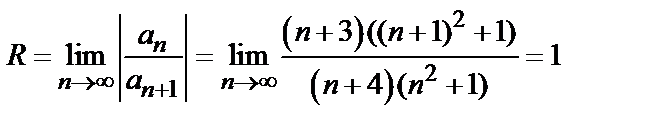 ,
,
Интервал сходимости данного ряда определяется интервалом 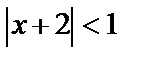 или
или 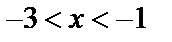 .
.
Исследуем концы интервала сходимости. При 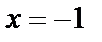 получаем числовой ряд
получаем числовой ряд
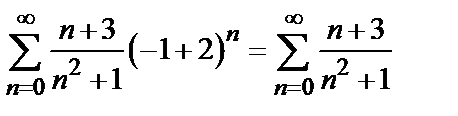 ,
,
расходимость которого может быть установлена с помощью предельного признака сравнения (эталонный ряд – гармонический).
При 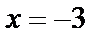 получаем числовой ряд
получаем числовой ряд
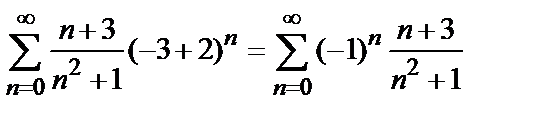 ,
,
который сходится по признаку Лейбница. Так как ряд, составленный из абсолютных членов данного ряда, т.е. ряд 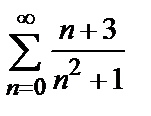 , расходится, то исследуемый ряд сходится условно.
, расходится, то исследуемый ряд сходится условно.
Таким образом, интервал сходимости исследуемого степенного ряда имеет вид 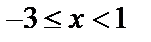 .
.
Задачи №421-450:
Исследовать сходимость рядов:
а) по признаку Даламбера;
б) по радикальному признаку Коши.
421. а) 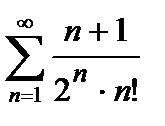
| б) 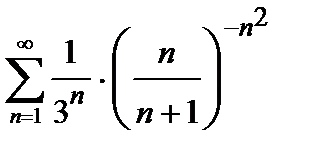
|
422. а) 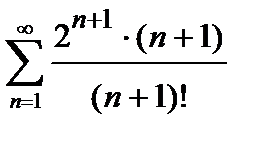
| б) 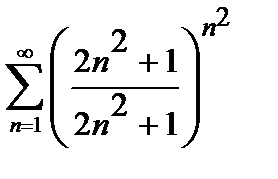
|
423. а) 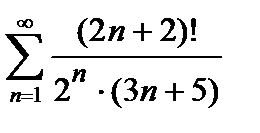
| б) 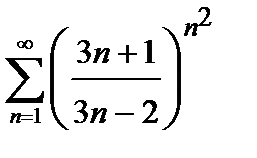
|
424. а) 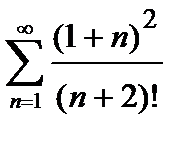
| б) 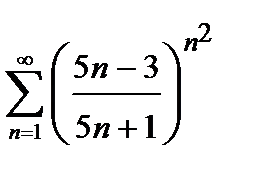
|
425. а) 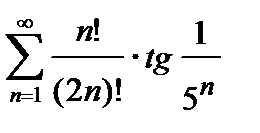
| б) 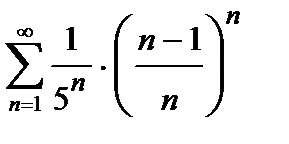
|
426. а) 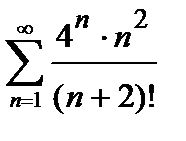
| б) 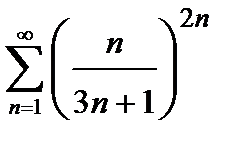
|
427. а) 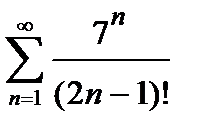
| б) 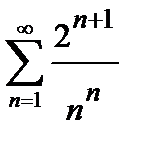
|
428. а) 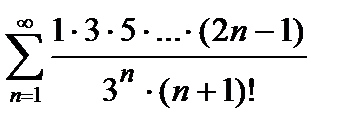
| б) 
|
429. а) 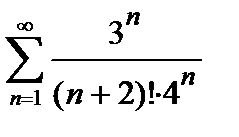
| б) 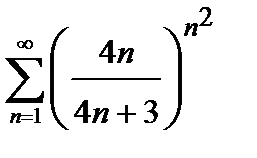
|
430. а) 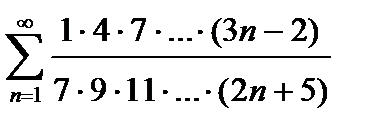
| б) 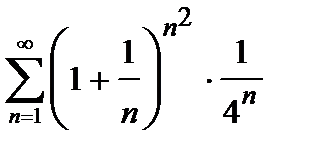
|
431. а) 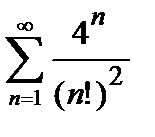
| б) 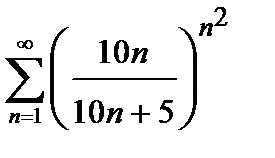
|
432. а) 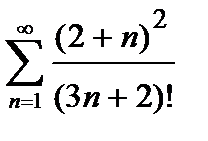
| б) 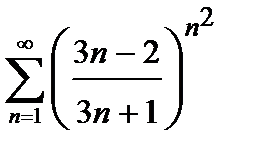
|
433. а) 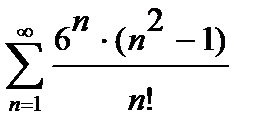
| б) 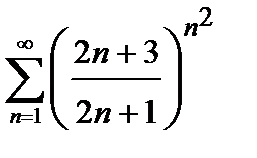
|
434. а) 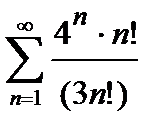
| б) 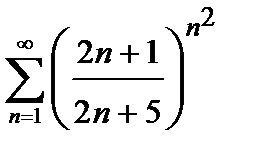
|
435. а) 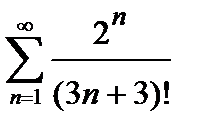
| б) 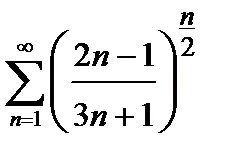
|
436. а) 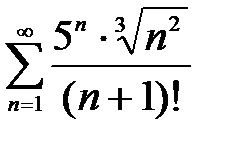
| б) 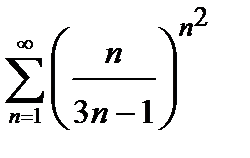
|
437. а) 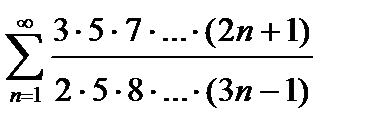
| б) 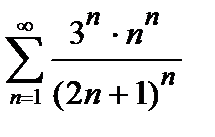
|
438. а) 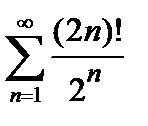
| б) 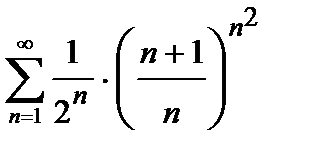
|
439. а) 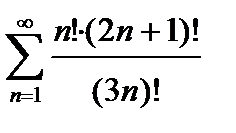
| б) 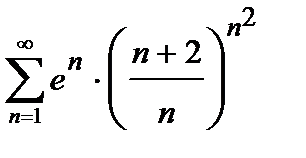
|
440. а) 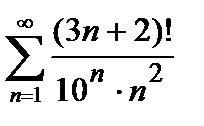
| б) 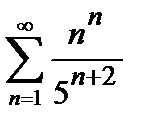
|
441. а) 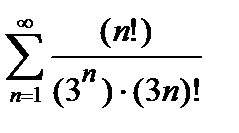
| б) 
|
442. а) 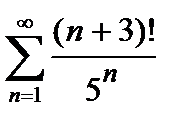
| б) 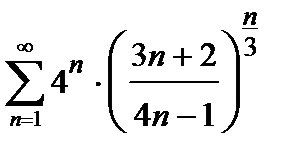
|
443. а) 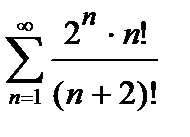
| б) 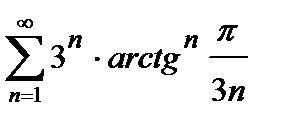
|
444. а) 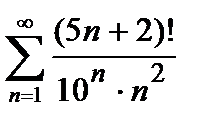
| б) 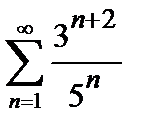
|
445. а) 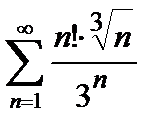
| б) 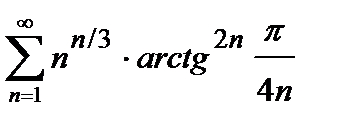
|
446. а) 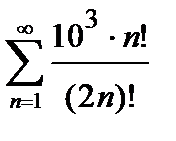
| б) 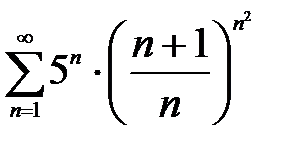
|
447. а) 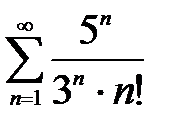
| б) 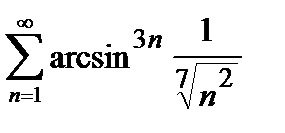
|
448. а) 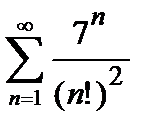
| б) 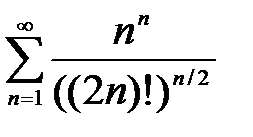
|
449. а) 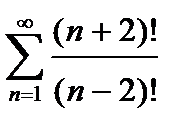
| б) 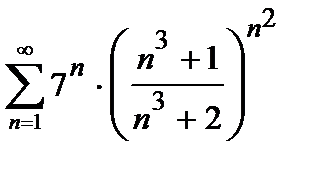
|
450. а) 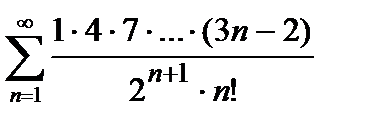
| б) 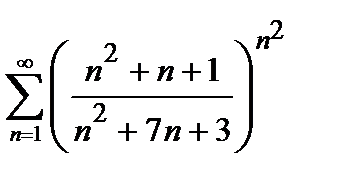
|
Задачи №451-480:
Исследовать на абсолютную и условную сходимость знакочередующиеся ряды:
451. 
|
|
|
|


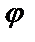 (х, С), которая при любом значении произвольной постоянной С является решением данного уравнения. Решения, получающиеся из общего решения y =
(х, С), которая при любом значении произвольной постоянной С является решением данного уравнения. Решения, получающиеся из общего решения y = 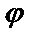 (х, С) при определенном значении произвольной постоянной С, называются частными. Задача нахождения частного решения, удовлетворяющего начальным условиям y=
(х, С) при определенном значении произвольной постоянной С, называются частными. Задача нахождения частного решения, удовлетворяющего начальным условиям y= 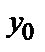 при
при 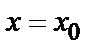 (другая запись
(другая запись 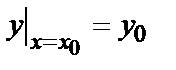 ), называется задачей Коши.
), называется задачей Коши. (х) данного дифференциального уравнения, построенный на плоскости хОy, называется интегральной кривой этого уравнения.
(х) данного дифференциального уравнения, построенный на плоскости хОy, называется интегральной кривой этого уравнения.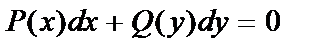 , (1)
, (1)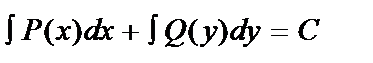 - его общий интеграл.
- его общий интеграл.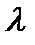 вся функция умножится на
вся функция умножится на 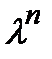 , то есть:
, то есть: 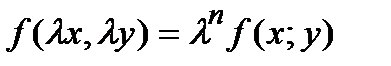 .
.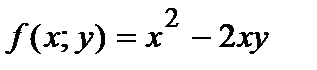 - однородная функция второго порядка, так как
- однородная функция второго порядка, так как 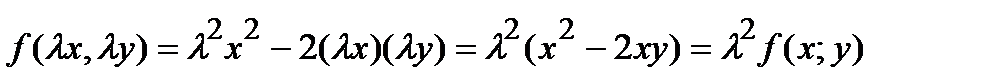 .
.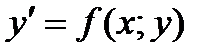 (2)
(2)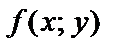 однородного нулевого порядка.
однородного нулевого порядка.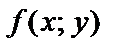 однородная функция нулевого порядка, то по определению
однородная функция нулевого порядка, то по определению 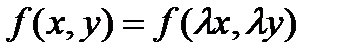 . Положив
. Положив 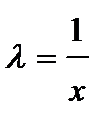 , получаем:
, получаем: 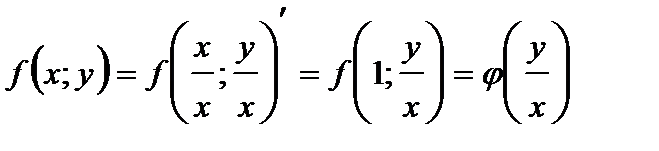 .
.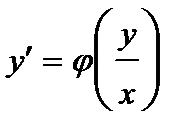 (3)
(3)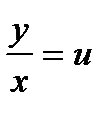 или
или 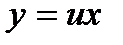 .
.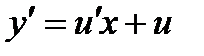 в уравнение (3) получаем:
в уравнение (3) получаем: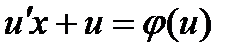 или
или 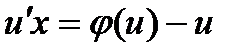 ,
,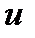 на
на 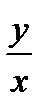 . Получим общее решение (интеграл) исходного уравнения.
. Получим общее решение (интеграл) исходного уравнения.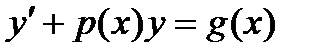 (4)
(4)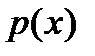 и
и 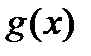 - некоторые (непрерывные) функции переменной х. В случае, когда
- некоторые (непрерывные) функции переменной х. В случае, когда 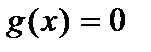 , уравнение называетсяоднородным; если
, уравнение называетсяоднородным; если 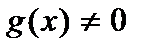
 неоднородным.
неоднородным.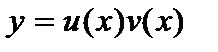 . Так как
. Так как 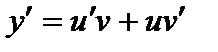 , то подставив в уравнение (4), получим:
, то подставив в уравнение (4), получим: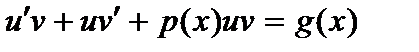 или
или 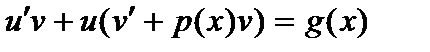 .
.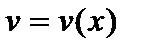 уравнения
уравнения 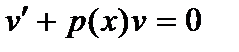 , тогда функция
, тогда функция 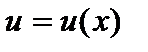 - решение уравнения
- решение уравнения 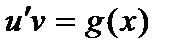 . Учитывая, что
. Учитывая, что 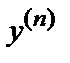 = f (х, у, у′,…,
= f (х, у, у′,…, 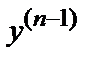 ).
).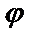 (х) данного уравнения, удовлетворяющего начальным условиям
(х) данного уравнения, удовлетворяющего начальным условиям 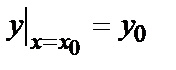 ;
; 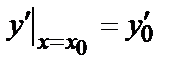 ;
; 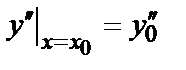 ; …;
; …; 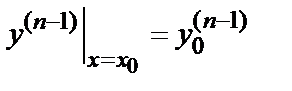 , называется задачей Коши.
, называется задачей Коши.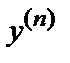 = f (х, у, у ′, …,
= f (х, у, у ′, …, 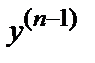 ) функция f (х, у, у ′,…,
) функция f (х, у, у ′,…, 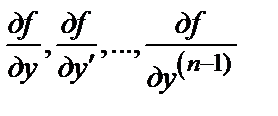 по аргументам у, у ′, …
по аргументам у, у ′, … 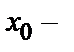 h < х <
h < х < 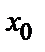 + h (h > 0), на котором существует единственное решение у =
+ h (h > 0), на котором существует единственное решение у = 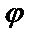 (х) данного уравнения, удовлетворяющее условиям у (
(х) данного уравнения, удовлетворяющее условиям у (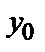 ; у ′(
; у ′(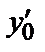 ; …;
; …; 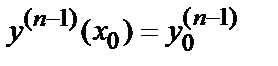 , где значения х =
, где значения х = 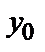 ; у ′=
; у ′= 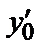 ; …;
; …; 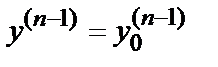 содержатся в области D.
содержатся в области D.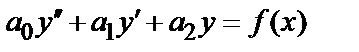 , где
, где 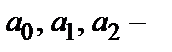 числа, причем
числа, причем 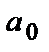 ≠0. Если f (х) = 0, то уравнение называется однородным, а если f(х)≠ 0 – неоднородным.
≠0. Если f (х) = 0, то уравнение называется однородным, а если f(х)≠ 0 – неоднородным.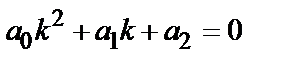 называется характеристическим уравнением дифференциального уравнения
называется характеристическим уравнением дифференциального уравнения 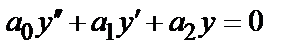 . Пусть D =
. Пусть D = 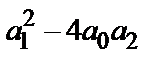 дискриминант квадратного уравнения. Возможны следующие случаи:
дискриминант квадратного уравнения. Возможны следующие случаи: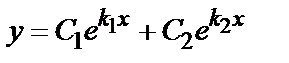 (
(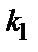 и
и 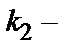 корни характеристического уравнения);
корни характеристического уравнения);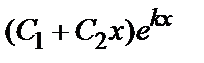 (k –корень характеристического уравнения);
(k –корень характеристического уравнения);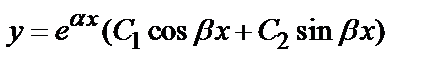 (
(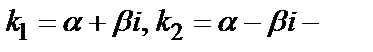 корни характеристического уравнения).
корни характеристического уравнения).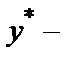 некоторое частное решение неоднородного уравнения
некоторое частное решение неоднородного уравнения 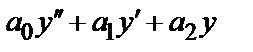 = f (х)и Y –общее решение соответствующего однородного уравнения
= f (х)и Y –общее решение соответствующего однородного уравнения 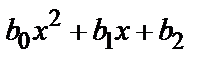 ; тогда:
; тогда: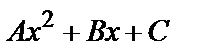 , если нуль не является корнем характеристического уравнения;
, если нуль не является корнем характеристического уравнения;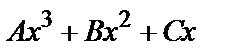 , если нуль является простым корнем характеристического уравнения;
, если нуль является простым корнем характеристического уравнения;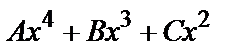 , если нуль является двукратным корнем характеристического уравнения.
, если нуль является двукратным корнем характеристического уравнения.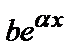 ; тогда:
; тогда: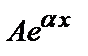 , если число
, если число 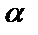 не является корнем характеристического уравнения;
не является корнем характеристического уравнения;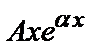 , если число
, если число 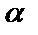 является корнем характеристического уравнения;
является корнем характеристического уравнения;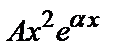 , если число
, если число 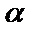 является двукратным корнем характеристического уравнения.
является двукратным корнем характеристического уравнения.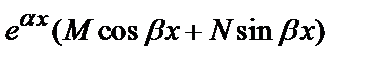 ; тогда:
; тогда: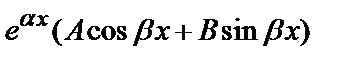 , если число
, если число 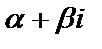 не является корнем характеристического уравнения;
не является корнем характеристического уравнения;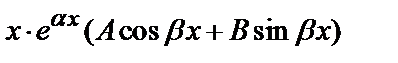 , если число
, если число 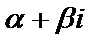 является корнем характеристического уравнения.
является корнем характеристического уравнения.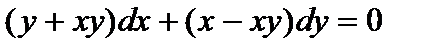 .
.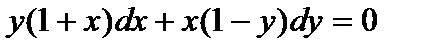 .
.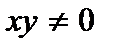 , получим
, получим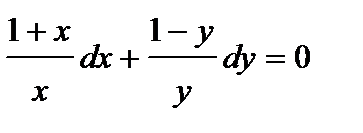 .
.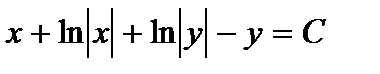 или
или 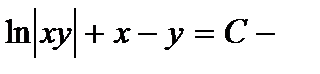 общий интеграл
общий интеграл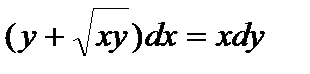 .
.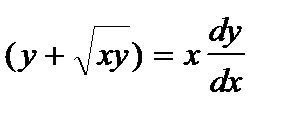 или
или 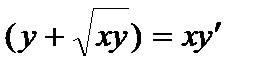 .
.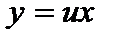 , тогда
, тогда 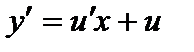 . Подставляя в последнее уравнение, получаем:
. Подставляя в последнее уравнение, получаем: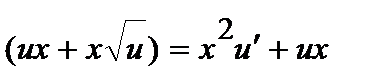 или
или 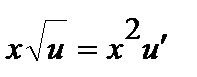 .
.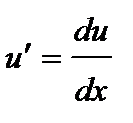 , получаем
, получаем 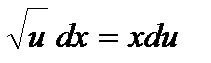 или
или 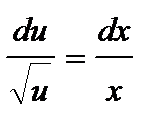 . Интегрируя почленно это уравнение, имеем:
. Интегрируя почленно это уравнение, имеем: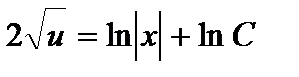 .
.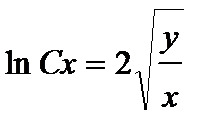 или
или 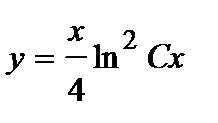 .
.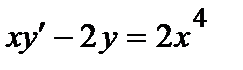 .
.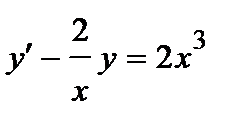 .
.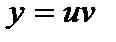 , тогда
, тогда 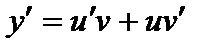 . Подставляя в последнее уравнение, получаем:
. Подставляя в последнее уравнение, получаем: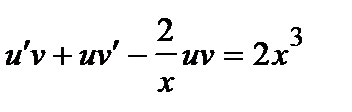 или
или 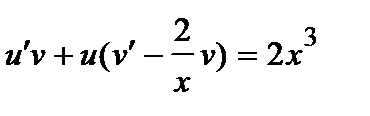 .
.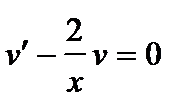 или
или 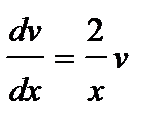 , откуда
, откуда 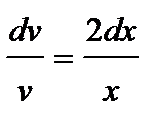 . Проинтегрировав, найдем какое-либо частное решение этого уравнения, например, при С =0 имеем
. Проинтегрировав, найдем какое-либо частное решение этого уравнения, например, при С =0 имеем 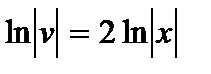 и
и 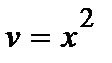 .
.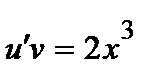 или
или 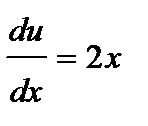 .
.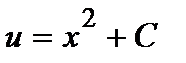 . Тогда окончательно имеем
. Тогда окончательно имеем 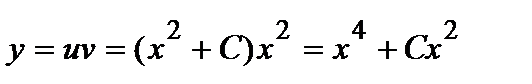 .
.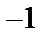 ; у ′(1)=0; у ′′(1)=1.
; у ′(1)=0; у ′′(1)=1. z =0
z =0 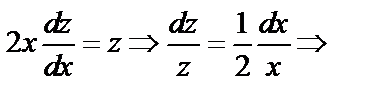
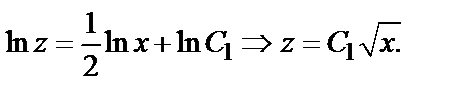
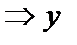 ′′=
′′= 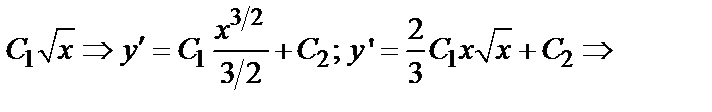
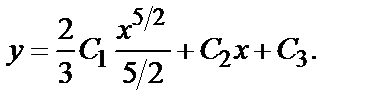 Следовательно, у =
Следовательно, у = 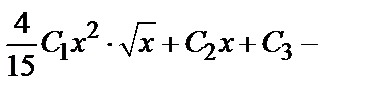 общее решение дифференциального уравнения.
общее решение дифференциального уравнения.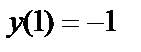
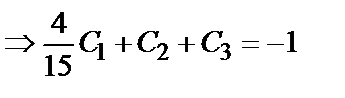 ;
;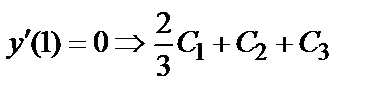 =0;
=0;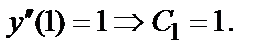
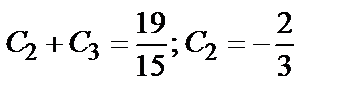 находим
находим 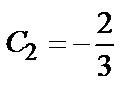 ;
; 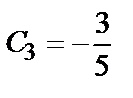 . Значит, искомое частное решение имеет вид:
. Значит, искомое частное решение имеет вид: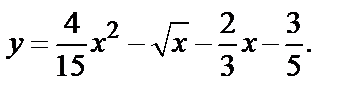
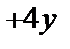 ′+13 у =5sin2 х и частное решение, удовлетворяющее начальным условиям
′+13 у =5sin2 х и частное решение, удовлетворяющее начальным условиям 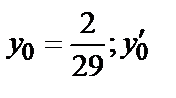 =
= 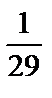 при х =0.
при х =0.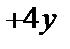 ′+13 у =0. Соответствующее характеристическое уравнение имеет вид
′+13 у =0. Соответствующее характеристическое уравнение имеет вид 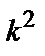 +4 k +13=0, откуда
+4 k +13=0, откуда 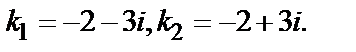 Следовательно, Y =
Следовательно, Y = 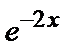
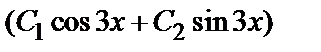 общее решение однородного уравнения.
общее решение однородного уравнения.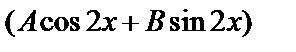 . Имеем:
. Имеем: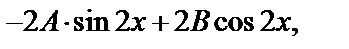 (у *)′′=
(у *)′′= 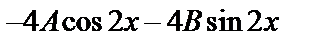 .
.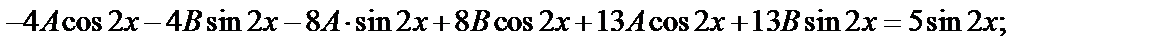
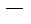 8 А +9 В)sin2 х =5sin2 х
8 А +9 В)sin2 х =5sin2 х
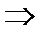
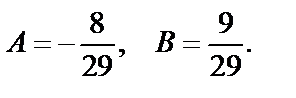
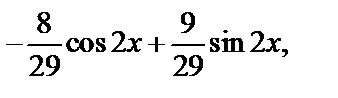
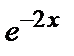
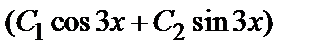
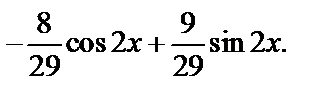
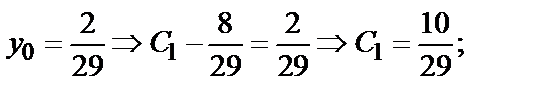
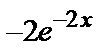
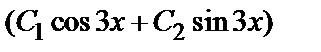 +
+ 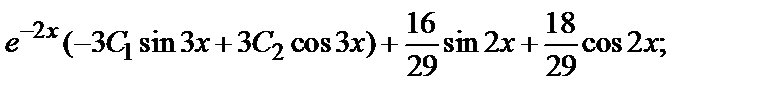
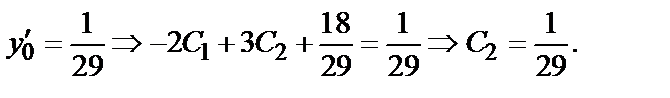
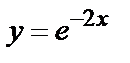
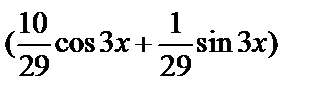
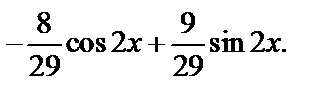
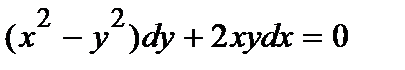
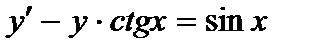
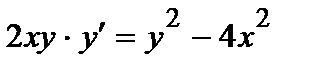
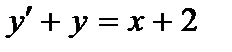
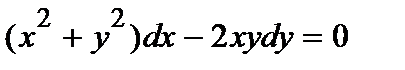
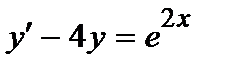
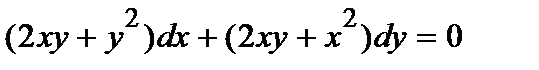
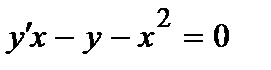
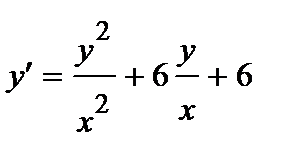
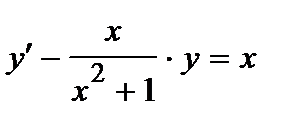
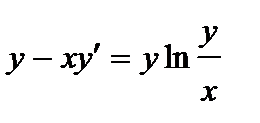
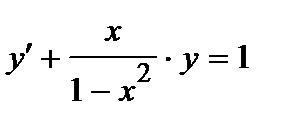
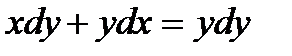
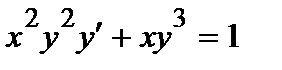
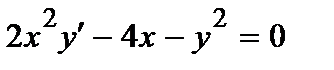
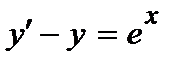
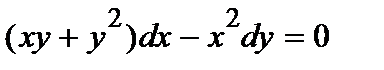
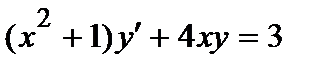
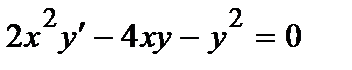
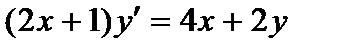
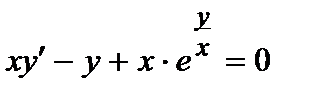
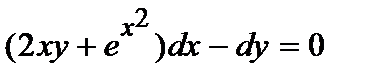
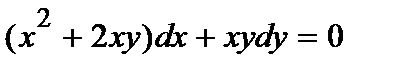
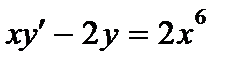
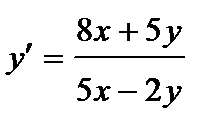
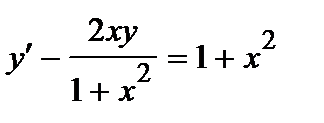
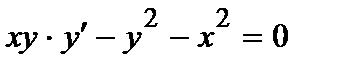
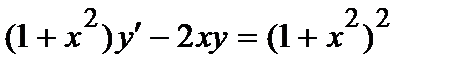
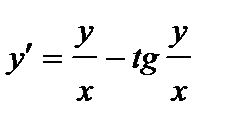
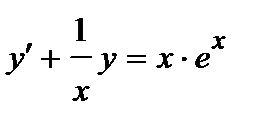
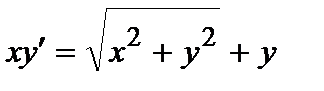
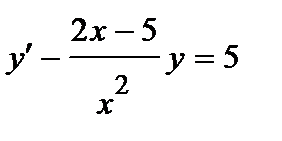
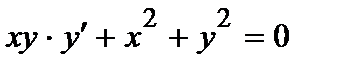
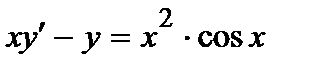
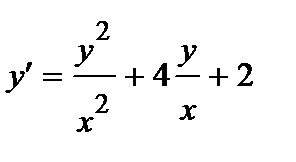
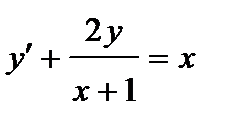
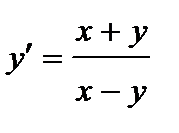
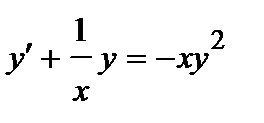
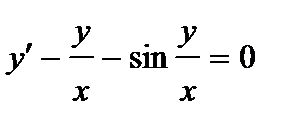
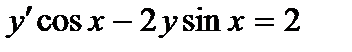
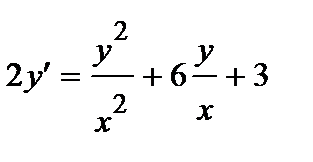
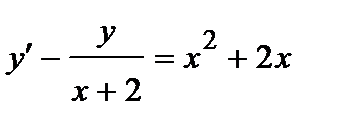
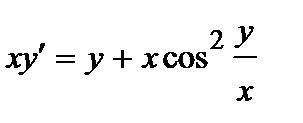
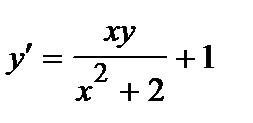
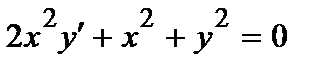
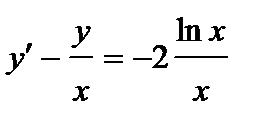
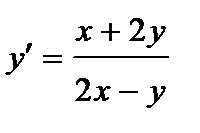
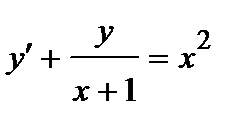
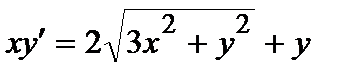
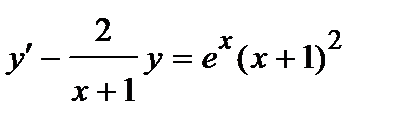
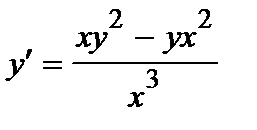
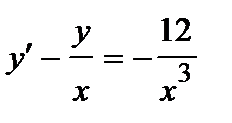
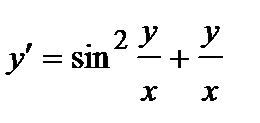
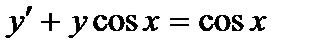
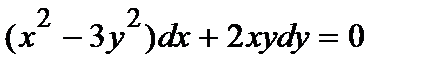
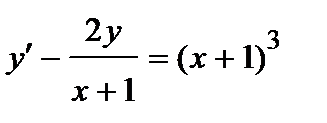
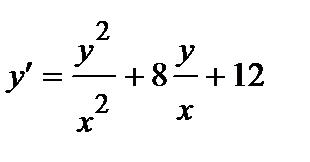
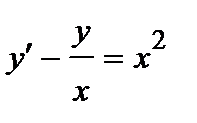
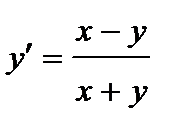
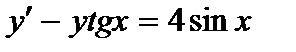
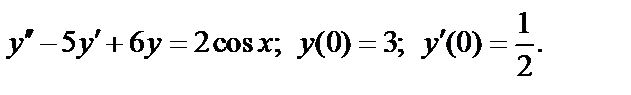
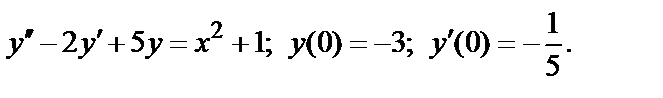
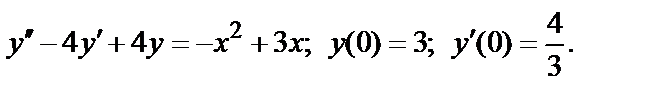
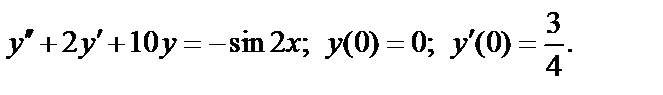
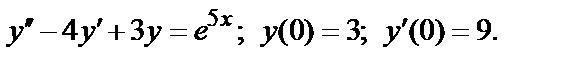
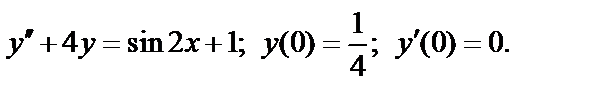
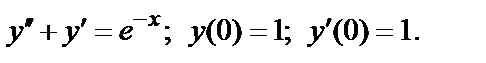
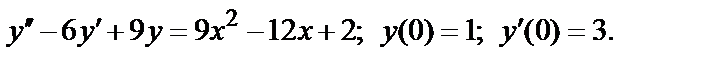
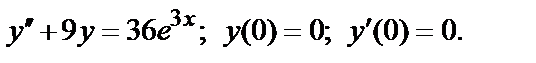
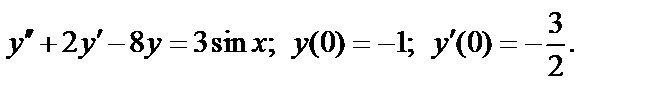
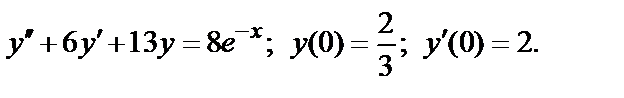
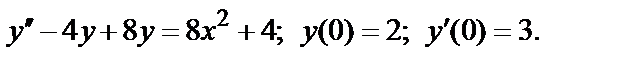
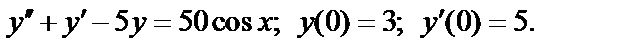
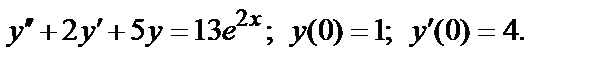
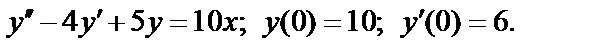
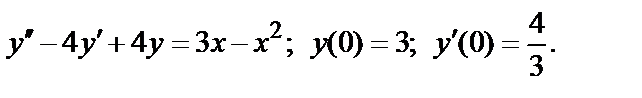
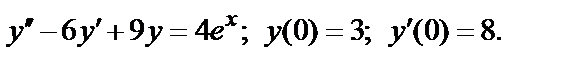
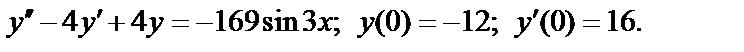
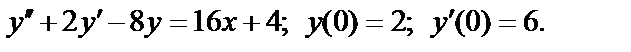
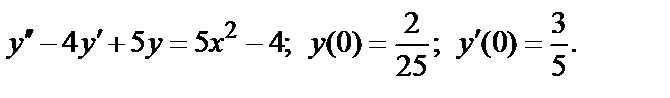
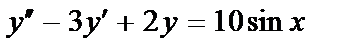 ;
; 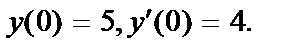
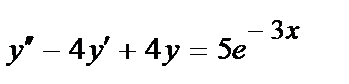 ;
; 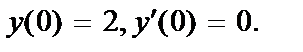
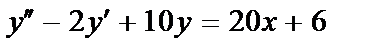 ;
; 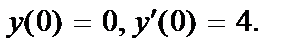
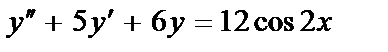 ;
; 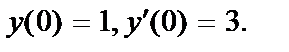
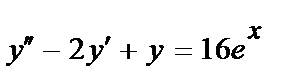 ;
; 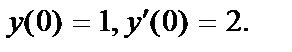
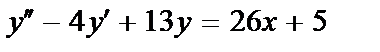 ;
; 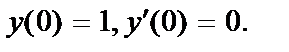
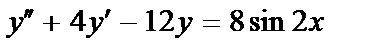 ;
; 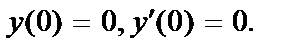
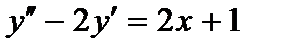 ;
; 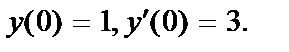
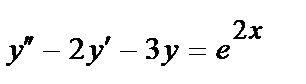 ;
; 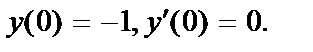
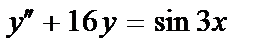 ;
; 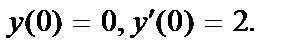
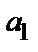 +
+ 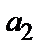 +…+ а
+…+ а 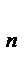 +… =
+… = 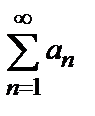 , (1)
, (1)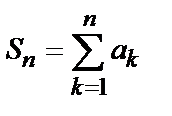 . Число
. Число 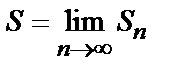 называется суммой ряда. Если же предел частичных сумм не существует, то ряд (1) называется расходящимися.
называется суммой ряда. Если же предел частичных сумм не существует, то ряд (1) называется расходящимися.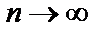 :
: 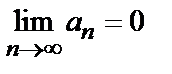 .
.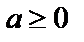 ) относятся:
) относятся: , (2)
, (2)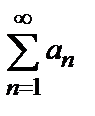 и
и 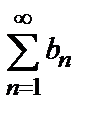 одновременно сходится или расходится. В качестве эталонных рядов для сравнения обычно служат:
одновременно сходится или расходится. В качестве эталонных рядов для сравнения обычно служат: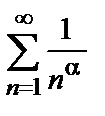 сходящийся при
сходящийся при 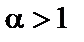 и расходящийся при
и расходящийся при 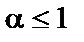 ;
;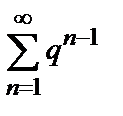 , сходящийся при
, сходящийся при 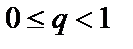 и расходящийся
и расходящийся 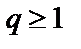 .
.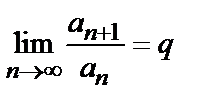 , (3)
, (3)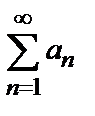 сходится при
сходится при 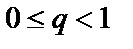 и расходится при
и расходится при 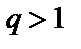 . Если же
. Если же 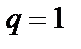 , то вопрос о сходимости ряда этим признаком не решается.
, то вопрос о сходимости ряда этим признаком не решается.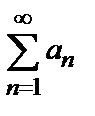 с членами, имеющими разные знаки, называется условно сходящимся, если ряд
с членами, имеющими разные знаки, называется условно сходящимся, если ряд 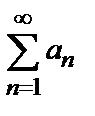 сходится, а ряд
сходится, а ряд 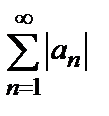 расходится, и абсолютно сходящимся, если ряд
расходится, и абсолютно сходящимся, если ряд 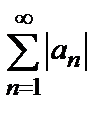 сходится.
сходится.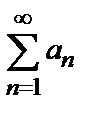 существует
существует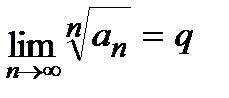 , (4)
, (4)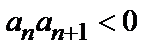 (т.е. ряд знакочередующийся);
(т.е. ряд знакочередующийся);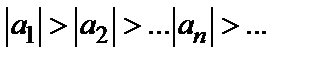 ;
;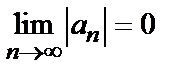 , то ряд сходится. Погрешность
, то ряд сходится. Погрешность  , происходящая от замены суммы сходящегося знакочередующегося ряда суммой его первых n членов, по абсолютной величине меньше первого из отброшенных членов:
, происходящая от замены суммы сходящегося знакочередующегося ряда суммой его первых n членов, по абсолютной величине меньше первого из отброшенных членов: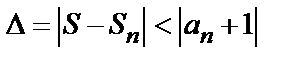 . (5)
. (5)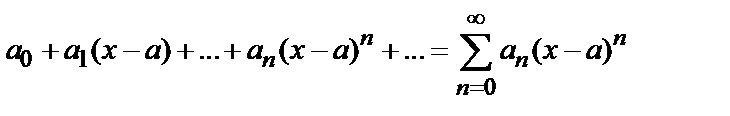 (6)
(6)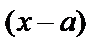 ], точка
], точка 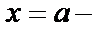 центром разложения,
центром разложения, 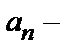 коэффициентами ряда. Число
коэффициентами ряда. Число 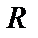 называется радиусом сходимости степенного ряда, если ряд (6) сходится при
называется радиусом сходимости степенного ряда, если ряд (6) сходится при 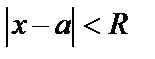 и расходится при
и расходится при 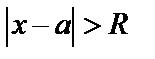 . При
. При 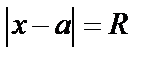 ряд может как сходится, так и расходится. Интервал
ряд может как сходится, так и расходится. Интервал 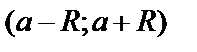 называется интервалом сходимости степенного ряда (6). Радиус сходимости R может быть найден по формуле
называется интервалом сходимости степенного ряда (6). Радиус сходимости R может быть найден по формуле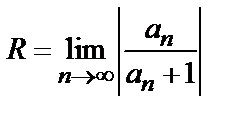 . (7)
. (7)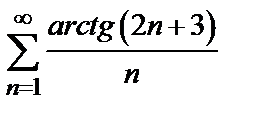 .
.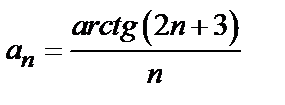 , то, заменяя в выражении n- го члена n на n +1, находим
, то, заменяя в выражении n- го члена n на n +1, находим 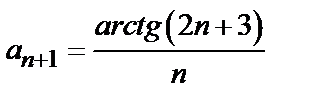 . Затем ищем предел отношения последующего члена
. Затем ищем предел отношения последующего члена 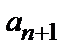 к предыдущему
к предыдущему 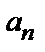 при
при 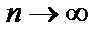 :
: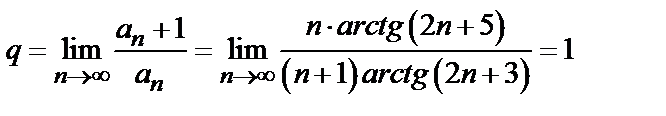 .
.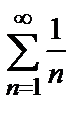 ,
, 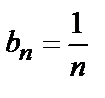 и в силу формулы (2) получим
и в силу формулы (2) получим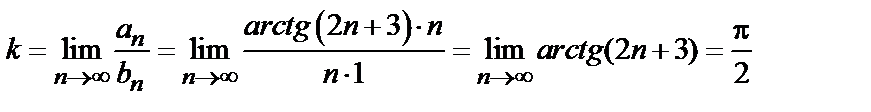 .
. расходится (гармонический ряд).
расходится (гармонический ряд).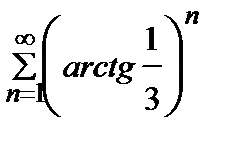 .
.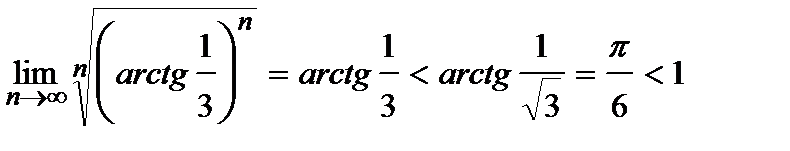
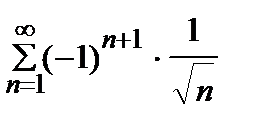 .
.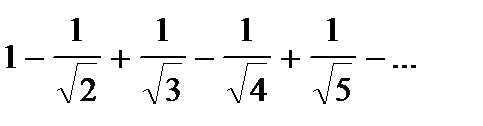 (т.е. ряд знакочередующийся);
(т.е. ряд знакочередующийся);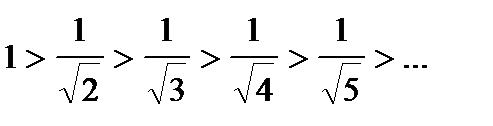 (монотонно убывают);
(монотонно убывают);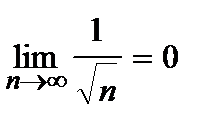 , то ряд сходится.
, то ряд сходится.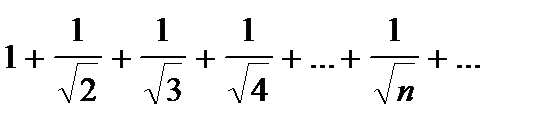 , общий член которого имеет вид
, общий член которого имеет вид 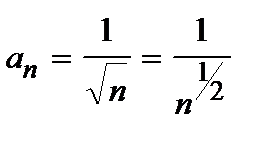 . Обобщенный гармонический ряд
. Обобщенный гармонический ряд 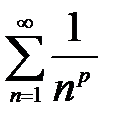 при p <1 расходится. Таким образом, исследуемый ряд сходится условно.
при p <1 расходится. Таким образом, исследуемый ряд сходится условно.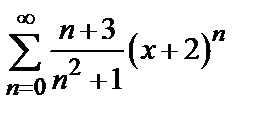 . Исследовать сходимость ряда на концах интервала сходимости.
. Исследовать сходимость ряда на концах интервала сходимости.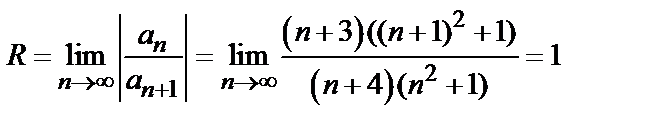 ,
,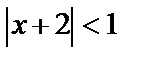 или
или 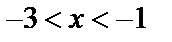 .
.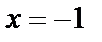 получаем числовой ряд
получаем числовой ряд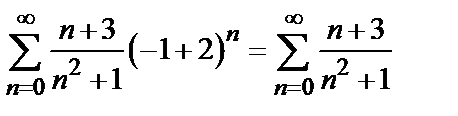 ,
,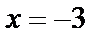 получаем числовой ряд
получаем числовой ряд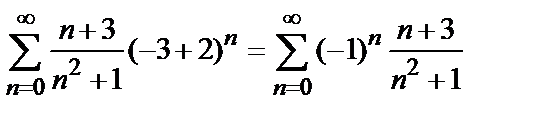 ,
,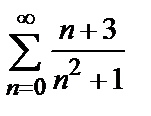 , расходится, то исследуемый ряд сходится условно.
, расходится, то исследуемый ряд сходится условно.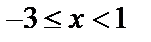 .
.