Пусть  определена на
определена на 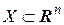 , и
, и  .
.
Определение 23. Внутренняя точка  называется точкой строгого локального максимума функции
называется точкой строгого локального максимума функции  , если существует такая окрестность точки
, если существует такая окрестность точки  , что
, что  и
и  , выполняется неравенство
, выполняется неравенство  .
.
Если  , то
, то  точка нестрогого локального максимума.
точка нестрогого локального максимума.
Если  , то
, то  точка строгого локального минимума.
точка строгого локального минимума.
Если  , то
, то  точка нестрогого локального минимума.
точка нестрогого локального минимума.
Точки локального максимума и минимума называются точками экстремума функции  .
.
Теорема 12 (необходимое условие экстремума). Если функция  дифференцируема в точке
дифференцируема в точке  и имеет в этой точке локальный (нестрогий) экстремум, то выполняются
и имеет в этой точке локальный (нестрогий) экстремум, то выполняются
 и
и  . (35)
. (35)
ƒ Так как по определению имеем
 ,
,  ,
,
то нужно доказать, что для  выполняются равенства
выполняются равенства  . Рассмотрим функцию
. Рассмотрим функцию  , у которой все переменные зафиксированы, кроме
, у которой все переменные зафиксированы, кроме  , а
, а  – направляющий вектор оси
– направляющий вектор оси  . Тогда, так как
. Тогда, так как  в точке
в точке  имеет экстремум, то
имеет экстремум, то  в точке
в точке  тоже имеет экстремум, как функции одной переменной. Отсюда согласно теореме Ферма
тоже имеет экстремум, как функции одной переменной. Отсюда согласно теореме Ферма  . Таким образом, из определения частной производной получаем:
. Таким образом, из определения частной производной получаем:
 , <
, <
Замечание. Условия (35) является необходимыми, но не достаточными. Например, функция  дифференцируемая в точке
дифференцируемая в точке 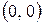 и
и
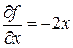 ,
,  ,
,  ,
,  ,
,
но экстремума в точке 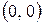 нет (рис. 4), так как в любой окрестности точки (0, 0)
нет (рис. 4), так как в любой окрестности точки (0, 0)  принимает как положительное, так и отрицательное значения.
принимает как положительное, так и отрицательное значения.
Определение 24. Точка  называется стационарной точкой функции
называется стационарной точкой функции  , если выполняется условие (35).
, если выполняется условие (35).
Стационарная точка  называется регулярной, если в этой точке существует второй дифференциал
называется регулярной, если в этой точке существует второй дифференциал  , (т.е. существуют все частные производные второго порядка) и он является невырожденной квадратичной формой переменных
, (т.е. существуют все частные производные второго порядка) и он является невырожденной квадратичной формой переменных  .
.

Так как матрица квадратичной формы  есть матрица Гессе
есть матрица Гессе  , то невырожденность квадратичной формы означает, что определитель матрицы Гессе
, то невырожденность квадратичной формы означает, что определитель матрицы Гессе  , который называется гессиан, не равен нулю.
, который называется гессиан, не равен нулю.
Теорема 13 (достаточное условие экстремума). Пусть функция  дважды дифференцируемой в окрестности точки
дважды дифференцируемой в окрестности точки  , где
, где  – стационарная точка, а второй дифференциал
– стационарная точка, а второй дифференциал  в точке
в точке  есть невырожденная квадратичная форма переменных
есть невырожденная квадратичная форма переменных  . Тогда:
. Тогда:
если  – положительная определенная квадратичная форма, то
– положительная определенная квадратичная форма, то  точка локального минимума;
точка локального минимума;
если  – отрицательная квадратичная форма, то
– отрицательная квадратичная форма, то  – точка максимума;
– точка максимума;
если  – знакопеременная квадратичная форма, то
– знакопеременная квадратичная форма, то  не является точкой экстремума.
не является точкой экстремума.
ƒ Так как  – стационарная точка, то из теоремы 12 следует
– стационарная точка, то из теоремы 12 следует
 и
и 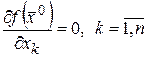 .
.
Запишем формулу Тейлора для случая m =2 с остаточным членом в форме Пеано
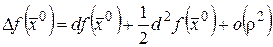 ,
,
где  ,
,  ,
,  .
.
Тогда формулу Тейлора можно переписать в виде
 . (36)
. (36)
Короткое (упрощенное) доказательство. Пусть второй дифференциал является отрицательно определенной квадратичной формой (функцией) в точке  . Тогда, при любых значениях
. Тогда, при любых значениях  в окрестности точки
в окрестности точки  , эта функция принимает отрицательное значение, т.е.
, эта функция принимает отрицательное значение, т.е. 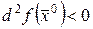 и из (36) следует, что
и из (36) следует, что  . Отсюда следует, что
. Отсюда следует, что  - точка максимума. Аналогично, остальное доказательство.
- точка максимума. Аналогично, остальное доказательство.
Подробное доказательство. Рассмотрим единичный вектор  сонаправленный с вектором, соединяющим
сонаправленный с вектором, соединяющим  и
и  :
:  ,
,  . Обозначим
. Обозначим  , где
, где 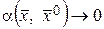 при
при  . Тогда
. Тогда

или
 . (37)
. (37)
Пусть второй дифференциал  есть положительно определенная квадратичная форма. Квадратичная форма
есть положительно определенная квадратичная форма. Квадратичная форма 
 задана на единичной сфере
задана на единичной сфере  , которая есть ограниченное замкнутое множество. По теореме Вейерштрасса функция n переменных
, которая есть ограниченное замкнутое множество. По теореме Вейерштрасса функция n переменных  достигает своего наименьшего значения на этом множестве, т.е. достигает нижней грани:
достигает своего наименьшего значения на этом множестве, т.е. достигает нижней грани:  и
и  .
.
Ясно, что 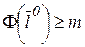 для произвольного значения
для произвольного значения  . Тогда из положительно определенности квадратичной формы и условия
. Тогда из положительно определенности квадратичной формы и условия  , следует, что
, следует, что 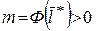 . Тогда
. Тогда
 ,
,  .
.
Так как  , то существует
, то существует  , что
, что  в
в  можно сделать не более любого наперед заданного числа, например
можно сделать не более любого наперед заданного числа, например  , т.е.
, т.е.
 ,
,  .
.
Из полученного соотношения и формулы (37) следует, что
 , т.к.
, т.к.

а откуда  , тогда
, тогда  – точка минимума.
– точка минимума.
Если второй дифференциал функции  есть отрицательно определенная квадратичная форма, то второй дифференциал функции
есть отрицательно определенная квадратичная форма, то второй дифференциал функции  в стационарной точке будет положительно определенной квадратичной формой. Тогда
в стационарной точке будет положительно определенной квадратичной формой. Тогда  – точка локального максимума функции
– точка локального максимума функции  .
.
Пусть  – знакопеременная квадратичная форма. Тогда существуют такие единичные векторы
– знакопеременная квадратичная форма. Тогда существуют такие единичные векторы  и
и 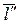 , что
, что
 ,
,
 .
.
По формуле (37) имеем
 ,
,
 ,
,
где  при
при  . Так как
. Так как  , то можно выбрать их сколь угодно малыми, так что слагаемые в скобках будут иметь фиксированные знаки. Тогда существует
, то можно выбрать их сколь угодно малыми, так что слагаемые в скобках будут иметь фиксированные знаки. Тогда существует  -окрестность точки
-окрестность точки  такая, что для
такая, что для  выполняются неравенства
выполняются неравенства

т.е. в любой сколько угодно малой окрестности точки  не выполняется определение экстремума. ■
не выполняется определение экстремума. ■
Следствие. Пусть  дважды дифференцируемая функция в окрестности стационарной точки
дважды дифференцируемая функция в окрестности стационарной точки  , тогда:
, тогда:
если  , то
, то  – точка минимума функции
– точка минимума функции  ;
;
если  , то
, то  – точка максимума функции
– точка максимума функции  ;
;
если  , то в точке
, то в точке  экстремума нет.
экстремума нет.
Справедливость следствия следует из критерия Сильвестра знакоопределенности квадратичных форм и теоремы 13. Здесь матрица Гессе имеет вид:
 ,
,
а гессиан есть определитель второго порядка  .
.
Пример. Для функции  найти точки экстремума или показать, что их нет.
найти точки экстремума или показать, что их нет.
Решение. Определим стационарные точки:
 ,
,
 .
.
Решая систему, получаем две точки 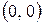 и
и  . Найдем матрицу Гессе:
. Найдем матрицу Гессе:
 .
.
Используя следствие, для точки 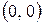 получаем
получаем
 ,
,

 .
.
Следовательно, в точке 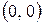 экстремума нет.
экстремума нет.
Для точки  получаем
получаем
 ,
,

 .
.
Следовательно,  точка локального минимума.
точка локального минимума.



 определена на
определена на 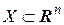 , и
, и  .
. , если существует такая окрестность точки
, если существует такая окрестность точки  , что
, что  и
и  , выполняется неравенство
, выполняется неравенство  .
. , то
, то  точка нестрогого локального максимума.
точка нестрогого локального максимума. , то
, то  , то
, то  .
. и
и  . (35)
. (35) ,
,  ,
, выполняются равенства
выполняются равенства  . Рассмотрим функцию
. Рассмотрим функцию  , у которой все переменные зафиксированы, кроме
, у которой все переменные зафиксированы, кроме  , а
, а  – направляющий вектор оси
– направляющий вектор оси  . Тогда, так как
. Тогда, так как  в точке
в точке  тоже имеет экстремум, как функции одной переменной. Отсюда согласно теореме Ферма
тоже имеет экстремум, как функции одной переменной. Отсюда согласно теореме Ферма  . Таким образом, из определения частной производной получаем:
. Таким образом, из определения частной производной получаем: , <
, < дифференцируемая в точке
дифференцируемая в точке 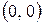 и
и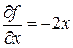 ,
,  ,
,  ,
,  ,
, принимает как положительное, так и отрицательное значения.
принимает как положительное, так и отрицательное значения. называется стационарной точкой функции
называется стационарной точкой функции  , (т.е. существуют все частные производные второго порядка) и он является невырожденной квадратичной формой переменных
, (т.е. существуют все частные производные второго порядка) и он является невырожденной квадратичной формой переменных  .
.
 , то невырожденность квадратичной формы означает, что определитель матрицы Гессе
, то невырожденность квадратичной формы означает, что определитель матрицы Гессе  , который называется гессиан, не равен нулю.
, который называется гессиан, не равен нулю. . Тогда:
. Тогда: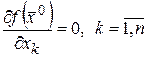 .
.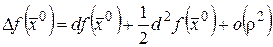 ,
, ,
,  ,
,  .
. . (36)
. (36) в окрестности точки
в окрестности точки 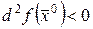 и из (36) следует, что
и из (36) следует, что  . Отсюда следует, что
. Отсюда следует, что  сонаправленный с вектором, соединяющим
сонаправленный с вектором, соединяющим  :
:  ,
,  . Обозначим
. Обозначим  , где
, где 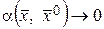 при
при  . Тогда
. Тогда
 . (37)
. (37) есть положительно определенная квадратичная форма. Квадратичная форма
есть положительно определенная квадратичная форма. Квадратичная форма 
 задана на единичной сфере
задана на единичной сфере  , которая есть ограниченное замкнутое множество. По теореме Вейерштрасса функция n переменных
, которая есть ограниченное замкнутое множество. По теореме Вейерштрасса функция n переменных  и
и  .
.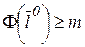 для произвольного значения
для произвольного значения  , следует, что
, следует, что 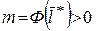 . Тогда
. Тогда ,
,  .
. , то существует
, то существует  , что
, что  в
в  можно сделать не более любого наперед заданного числа, например
можно сделать не более любого наперед заданного числа, например  , т.е.
, т.е. ,
,  .
. , т.к.
, т.к.
 в стационарной точке будет положительно определенной квадратичной формой. Тогда
в стационарной точке будет положительно определенной квадратичной формой. Тогда  .
. и
и 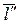 , что
, что ,
, .
. ,
, ,
, при
при  . Так как
. Так как  , то можно выбрать их сколь угодно малыми, так что слагаемые в скобках будут иметь фиксированные знаки. Тогда существует
, то можно выбрать их сколь угодно малыми, так что слагаемые в скобках будут иметь фиксированные знаки. Тогда существует  -окрестность точки
-окрестность точки  выполняются неравенства
выполняются неравенства
 , тогда:
, тогда: , то
, то  – точка минимума функции
– точка минимума функции  ;
; , то
, то  – точка максимума функции
– точка максимума функции  , то в точке
, то в точке  ,
, .
. найти точки экстремума или показать, что их нет.
найти точки экстремума или показать, что их нет. ,
, .
. . Найдем матрицу Гессе:
. Найдем матрицу Гессе: .
. ,
,
 .
. ,
, .
.


