Случайные события
Литература. [3], гл. I; [4], гл 1 – 4.
Рассмотрим решения некоторых задач на определение вероятностей событий, в которых используются теоремы сложения вероятностей, умножения вероятностей, формула полной вероятности.
Пример 1. В урне находится 7 белых и 5 красных шаров. Из урны вынимается один шар, отмечается его цвет и шар возвращается в урну. После этого из урны берется еще один шар. Найти вероятность того, что:
а) оба вынутых шара будут белыми;
б) оба вынутых шара будут одного цвета.
Решение:
В данной задаче опыт или испытание состоит в том, что из урны последовательно вынимают два шара (с возвращением). Рассмотрим следующие события:
A – первый вынутый шар белого цвета;
A – противоположное событию А событие, состоящее в том, что первый вынутый шар окажется красным;
B – второй вынутый шар белого цвета;
B - второй вынутый шар красного цвета;
C – оба вынутых шара белого цвета;
D – оба вынутых шара одного цвета;
В пункте а) надо найти вероятность
P (C)
события C. Событие C равно
произведению событий A и B, т. е. событие C состоит в том, что в результате опыта произойдут вместе событие A и событие B: C = A ⋅ B
События A и B - независимые, т.е. вероятность каждого из них не зависит от того,
что появится другое событие или нет. По теореме умножения вероятностей
P (C) = P (A) ⋅ P (B) =
7 ⋅ 7 = 49


 12 12 144
12 12 144
В пункте б) надо найти вероятность
P (D)
события D, которое состоит в том, что
либо первый и второй шары будут оба белыми A ⋅ B, либо первый и второй шары


будут оба красными A ⋅ B. Таким образом, событие D равно сумме событий A ⋅ B и
A ⋅ B:
D = A ⋅ B + A ⋅ B
События A ⋅ B


и A ⋅ B
несовместные, поэтому по теореме сложения вероятностей
вероятность события D будет равна
P (D) = P (A ⋅ B + A ⋅ B)= P (A ⋅ B) + P (A ⋅ B)
Воспользуемся теоремой умножения вероятностей независимых событий, тогда
P (D) = P (A) ⋅ P (B) + P (A)⋅ P (B)=

 = 7 ⋅ 7 +
= 7 ⋅ 7 +
5 ⋅ 5
= 37


 12 12 12 12 72
12 12 12 12 72
Отметим, что вероятности событий классической вероятности:
 P (A)= m,
P (A)= m,
n
A, B, A, B были найдены по формуле
где n - число всех равновероятных исходов эксперимента; m - число благоприятных событию A исходов.
Ответ: а)
 144
144
 ; б).
; б).
Пример 2. В урне находится 3 белых и 7 черных шаров. Из урны случайным образом вынимаются два шара. Найти вероятность того, что эти шары разных цветов.
Решение: Опыт состоит в том, что вынимаются два шара. Рассмотрим следующие события:
A - первый вынутый шар белый;
A - первый шар – черный;
B - второй шар – белый;
B - второй шар – черный;
C - вынутые шары разных цветов.
Событие C можно представить следующим образом:
C = A ⋅ B + A ⋅ B

События A ⋅ B

и A ⋅ B
- несовместные, поэтому


P (C) = P (A ⋅ B)+ P (A ⋅ B)
События A и B зависимые, поэтому вероятность
P (A ⋅ B)
по теореме умножения
вероятностей равна вероятности
P (A)
первого события A, умноженной на условную
вероятность произошло:

P (B | A)

второго события B при условии, что первое событие A

 P (A ⋅ B)= P (A)⋅ P (B | A)= 3
P (A ⋅ B)= P (A)⋅ P (B | A)= 3
⋅ 7.
Аналогично
10 9


 P (A ⋅ B)= P (A)⋅ P (B | A)= 7
P (A ⋅ B)= P (A)⋅ P (B | A)= 7
⋅ 3.
Поэтому




 P (C) =
P (C) =
3 ⋅ 7 + 7 ⋅ 3 = 7.
10 9
Ответ:
10 9 10 9 15
 .
.
Пример 3. Вероятность установления в данной местности устойчивого снежного покрова с октября равна 0,1. Определить вероятность того, что в ближайшие три года в этой местности устойчивый снежный покров с октября установится по крайней мере один раз.
Решение. Рассмотрим следующие события:
A 1 - в первый ближайший год устойчивый снежный покров установится с октября;
A 2 - во второй ближайший год – установится с октября;
A 3 - в третий ближайший год – установится с октября;
A - в ближайшие три года устойчивый снежный
покров установится с октября по крайней мере один раз;
A - в ближайшие три года с октября не будет ни разу устойчивого снежного покрова.
Найдем вероятность
P (A):




P (
A) =1−
P (
A)=1−
P (
A 1⋅
A 2⋅
A 3)=
=1− P (A 1)⋅ P (A 2)⋅ P (A 3)=
=1−(1−0,1)(1−0,1)(1−0,1) =1−(0,9)3=0,271
Ответ: 0, 271.
Пример 4. Для посева заготовлены семена пшеницы первого сорта, содержащие 1% примесей второго сорта и 3% примесей третьего сорта. Вероятность того, что из зерна вырастет колос, содержащий не мене 50 зерен, равна для первого сорта – 0,5, для второго сорта – 0,2, для третьего сорта – 0,05. Найти вероятность того, что из взятого наудачу зерна вырастет колос, содержащий не менее 50 зерен.
Решение:
Рассмотрим события:
A - событие, состоящее в том, что из наудачу взятого зерна вырастет колос, содержащий не менее 50 зерен;
H 1 - событие, состоящее в том, что наудачу взятое зерно окажется первого сорта;
H 2 - событие, состоящее в том, что наудачу взятое зерно окажется второго сорта;
H 3 - событие, состоящее в том, что наудачу взятое зерно окажется третьего сорта. По условию задачи имеем:
P (H 1) = 0,96;
 P (A H 1) = 0,5;
P (A H 1) = 0,5;
P (H 2) = 0,01;
 P (A H 2) = 0,2;
P (A H 2) = 0,2;
P (H 3) = 0,03
 P (A H 3) = 0,05
P (A H 3) = 0,05
Применяя формулу полной вероятности, получаем:
P (A) = P (H 1) ⋅ P (A | H 1) + P (H 2) ⋅ P (A | H 2) + P (H 3) ⋅ P (A | H 3),
P (A) = 0,96 ⋅ 0,5 + 0,01⋅ 0, 2 + 0,03 ⋅ 0,05 = 0, 4835
Ответ: 0, 4835.
Задачи 701 – 710
701) Три стрелка производят по одному выстрелу в цель. Вероятности попадания равны: для первого стрелка -- 0,6, для второго -- 0,7, для третьего -- 0,8. Найти вероятность одного попадания в цель.
702) Произведен залп из двух орудий по мишени. Вероятность попадания из первого орудия равна 0,85, из второго - 0,91. Найти вероятность поражения цели.
703) Вероятность попадания в мишень для первого стрелка - 0,8, а для второго - 0,6. Стрелки независимо друг от друга сделали по одному выстрелу. Какова вероятность того, что в мишень попадет только один из стрелков?
704) Рабочий обслуживает 4 станка. Вероятность того, что в течении часа первый станок не потребует внимания рабочего, равна 0,7; для второго станка эта вероятность равна 0,8; для третьего -- 0,9; для четвертого -- 0,85. Найти вероятность того, что в течении часа по крайней мере один станок потребует к себе внимания рабочего.
705) Экзаменационный билет содержит 3 вопроса. Вероятности того, что студент ответит на первый и второй вопросы билета, равны 0,9; на третий -- 0,8. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить хотя бы на два вопроса.
706) Детали проходят три операции обработки. Вероятность получения брака на первой операции равна 0,02, на второй - 0,03, на третьей - 0,02. Найти вероятность получения детали без брака после трех операций, предполагая, что получение брака на отдельных операциях являются независимыми событиями.
707) Пусть вероятность того, покупателю женской обуви потребуется обувь 37 размера, равна 0,25. Найти вероятность того, что из четырех первых покупателей обувь этого размера потребуется хотя бы одному.
708) Четыре охотника договорились стрелять по дичи в определенной последовательности. Следующий охотник производит выстрел лишь в случае промаха предыдущего. Вероятности попадания в цель каждым из охотников одинаковы и равны по 0,7. Найти вероятность того, что будет произведено три выстрела.
709) В двух ящиках находятся детали: в первом - 12 (из них 4 стандартных), во втором - 18 (из них 15 стандартных). Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что обе детали окажутся стандартными.
710) В студии телевидения 3 телевизионные камеры. Для каждой камеры вероятность того, что она включена в данный момент, равна 0,7. Найти вероятность того, что в данный момент включена хотя бы одна камера.
Задачи 711 – 720
711) На базе находятся костюмы, изготовленные на трех фабриках. Из них 30% изготовлено на первой, 50% на второй и 20% на третьей фабрике. Известно, что из каждых 100 костюмов, изготовленных на первой фабрике, знак качества имеют 60. Для второй и третьей фабрик этот показатель равен, соответственно, 70 и 80.Определить вероятность того, что взятый наугад с базы костюм не будет иметь знака качества.
712) В магазин поступают одинаковые электрические утюги. Первый завод поставляет 80%, второй - 20% всей продукции. Известно, что первый завод выпускает 90% продукции первого сорта, второй - 95%. Какова вероятность того, что проданный покупателю утюг партии первого сорта?
713) Электролампы изготавливаются на трёх заводах. Первый завод производит 45\% общего количества электроламп, второй -- 40%, третий -- 15%. Продукция первого завода содержит 70% стандартных ламп, второго -- 80%, третьего -- 81%
. В магазины поступает продукция всех трех заводов. Какова вероятность того, что купленная в магазине лампа окажется стандартной?
714) На сборку попадают детали с трех автоматов. Известно, что первый автомат дает
0,3% брака, второй -- 0,2% и третий -- 0,4%. С первого автомата поступило 1000, со второго -- 2000 и с третьего -- 2500 деталей. Какова вероятность попадания на сборку бракованной детали?
715) На фабрике, изготавливающей болты, первый станок производит -- 25%, второй
-- 35%, третий -- 40 % всех изделий. В их продукции брак составляет соответственно 5%, 4% и 2%. Какова вероятность того, что случайно выбранный болт дефектный?
716) Электрические лампочки производятся на двух заводах, причем первый из них поставляет 70%, а второй 30% всей поставляемой продукции. Из каждых 100 лампочек первого завода в среднем 83 стандартных, а из 100 лампочек второго завода - лишь 63 стандартных. Найти вероятность того, что взятая наудачу лампочка окажется стандартной.
717) Прибор может работать в двух режимах: нормальном и ненормальном.
Нормальный режим наблюдается в 80% всех случаев работы прибора;
ненормальный - в 20%. Вероятность выхода прибора из строя за время в нормальном режиме равна 0,2; в ненормальном - 0,6. Найти вероятность выхода прибора из строя за время.
718) В группе спортсменов 15 лыжников, 8 конькобежцев и 7 бегунов. Вероятность выполнить квалификационную норму для лыжника равна 0,8, для конькобежца - 0,7, для бегуна - 0,9. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму.
719) В хозяйстве имеется 6 гусеничных и 4 колесных трактора. Гусеничный трактор работает надежно с вероятностью 0,95, а колесный с вероятностью 0,8. Какова вероятность, что случайно выбранный для работы трактор будет работать надежно?
720) В группе стрелков два мастера спорта, три кандидата в мастера и пять перворазрядников. Мастер спорта попадает в десятку с вероятностью 95%, кандидат в мастера с вероятностью 90%, перворазрядник с вероятность 80%. Какова вероятность, что случайно выбранный стрелок попадёт в десятку?
Случайные величины
Литература. [4], гл. 6, 7, 8, 10, 11, 12.
Случайная величина, т. е. величина, значение которой зависит от случая, может быть “дискретной” – это когда она может принимать только отдельные, изолированные значения (например, номер, который достанется участнику соревнований) и “непрерывной” – это когда она может принимать все значения из некоторого промежутка (например, время, за которое спортсмен пробежит дистанцию).
Задать закон распределения дискретной случайной величины – это значит указать все ее возможные значения и указать вероятности этих значений. Например, если случайная величина X - это число выпадения герба при двух бросках монеты, то возможные значения такой случайной величины –это 0, 1, 2. Вероятности этих значений соответственно 0,25; 0,5; 0,25. Как это подсчитать покажем ниже. Обычно возможные значения и их вероятности принято записывать в таблицу:
Если такая таблица записана, то говорят, что закон распределения данной дискретной случайной величины известен.
Непрерывная случайная величина задается иначе. Для нее указывают либо так
называемую “интегральную” функцию распределения
F (x) = P (X
< x), т. е.
функцию, равную вероятности того, что в результате испытания случайная величина
X примет значение, меньше x, либо указывают производную от этой функции
F (x),
обозначаемую через
f (x) = F '(x).
f (x), так называемую “плотность вероятности”. То есть
В зависимости от вида функции
f (x)
говорят о том или другом законе
распределения вероятностей данной непрерывной случайной величины. Например, а) Закон равномерного распределения – если
0
f (
x) =
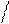
при при при
x < a
a < x < b b < x
где постоянная имеет вид:
C = 1 (b − a). Заметим, что в этом случае интегральная функция
0
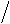
F (
x)=
x
(b − a)
при при при
x < a
a < x < b b < x
b) Показательный закон распределения – если
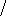 x > 0.
x > 0.
f (x) = 0 при
x < 0 и
f (x) = λ e −λ x
при
c) Нормальный закон распределения – если
f (x) =
1 e −(x − m)2
2σ2.
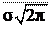 Если закон распределения известен, появляется возможность вычислить все
Если закон распределения известен, появляется возможность вычислить все
характеристики данной случайной величины. Наиболее известны следующие характеристики:
1. Математическое ожидание
M (X), определяющее “среднее значение” величины
X. Для дискретной случайной величины
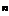
M (X) = ∑ xi ⋅ pi, т. е. это сумма
i =1
произведений возможных значений на их вероятности.
∞
Для непрерывной случайной величины M (X) = ∫ xf (x) dx
−∞
2. Дисперсия
D (X), характеризующая “степень рассеяния” возможных значений
случайной величины X вокруг ее среднего значения M (X).
По определению
D (X)= M (X − M (X))2или
D (X)= M (X 2)− (M (X))2,
что дает для дискретной случайной величины
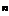
D (
X) = ∑
xi
i =1
⋅ pi − (M (x)),
а для непрерывной случайной величины
D (X) =
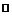
∫ x 2 f (x) dx − (M (x))2.
−∞
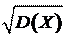 3. Среднее квадратическое отклонение σ(X) =.
3. Среднее квадратическое отклонение σ(X) =.
Если известны функции
F (x) и
f (x), легко вычислить вероятность попадания
случайной величины X в любой интервал (a, b):
P (a < X
< b) = F (b) − F (a) или, соответственно
P (a < X
b
< b) = ∫ f (x) dx.
a
Для нормального закона распределения этот интеграл просчитан и выражен через
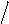 так называемую функцию Лапласа Ф (x)
так называемую функцию Лапласа Ф (x)
так, что
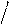 P (a < X < b)= Ф ((b − m)
P (a < X < b)= Ф ((b − m)
σ)− Ф ((a − m)
σ).
Для решения контрольных заданий укажем здесь, что Ф (− x) = − Ф (x) и что
Ф (0) = 0;
Ф (1) = 0,3413;
Ф (2) = 0, 4772;
Ф (3) = 0, 49865;
Ф (4) = 0, 49997; Ф (5) = 0, 49999.
Более подробные значения функции Лапласа можно найти в рекомендованных выше учебниках.
Пример 1. Случайная величина X - это число выпадения герба при двух бросках монеты. Построить закон распределения этой случайной величины и найти ее
математическое ожидание
отклонение σ(X).
M (X), дисперсию
D (x)
и среднее квадратическое
Решение: По формуле Бернулли число k появление события A в n испытаниях
имеет вероятность
P (k) = Ck pk qn − k. В данной задаче число p, т. е. вероятность
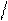
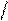
выпадения герба, равно 1 2. Соответственно
q тоже равно 1 2.
Поэтому вероятность того, что при двух бросках герб не выпадет ни разу, т. е. что
случайная величина X примет значение x = 0, будет равна
P (0) = C 0 p 0 q 2 = 1⋅1⋅ 1 = 1.


2 2 4 4
Вероятность одного выпадения герба, т. е. вероятность того, что X примет значение
x = 1 будет равна
P (1) = C 1 p 1 q 1 = 2 ⋅ 1 ⋅ 1 = 1.




2 2 1 2 2 2
И, наконец, вероятность того, что оба броска закончатся выпадением герба, т. е.
случайная величина X примет значение x = 2, будет равна
P (2) = C 2 p 2 q 0 = 2 ⋅1 ⋅ 1 ⋅1 = 1.
2 2 1⋅ 2 4 4
Итак, получаем такой закон распределения
X 0 1 2
P 0,25 0,5 0,25
Теперь находим M (X), D (x) и σ(X).
3 1 1 1



M (
X) =∑
xi pi =
x 1
p 1 +
x 2
p 2 +
x 3
p 3 =0⋅ +1⋅ +2⋅ =1
i =1
3 2 2
2 2 2 3
D (X) = ∑ xi
i =1
pi − (M (x))
= x 1
p 1 + x 2
p 2 + x 3
p 3 − (1) =



 = 0 ⋅ 1 + 1⋅ 1 + 4 ⋅ 1 −1 = 1
= 0 ⋅ 1 + 1⋅ 1 + 4 ⋅ 1 −1 = 1
4 2 4 2
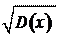
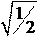 σ(X) = = ≈ 0,707
σ(X) = = ≈ 0,707
Ответ: M
(X) = 1;
D (x) = 0,5;
σ(X) = 0,707.
Пример 2. Найти математическое ожидание
M (X)
и среднее квадратичное
отклонение
σ(X)
непрерывной случайной величины X, если плотность
f (x) = 0
при
x < 0, и равна
f (x) = 5 e −5 x
при
x ≥ 0. Как называется закон распределения такой
случайной величины?
Решение:
∞ 0 ∞ ∞
M (x)= ∫ xf (x) dx = ∫ x 0 dx + ∫ x 5 ⋅ e −5 xdx = −∫ xd (e −5 x)=
−∞ −∞ 0 0
 = − xe −5 x ∞
= − xe −5 x ∞
∞−∞
+ ∫
∞
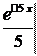
 e −5 xdx = 0 − = 1 5
e −5 xdx = 0 − = 1 5
0 0
Мы использовали метод интегрирования по частям, а также, что
 − xe −5 x ∞ = lim x = lim 1 = 0
− xe −5 x ∞ = lim x = lim 1 = 0
0 x →∞
e 5 x
x →∞
5 e 5 x
по правилу Лопиталя.
∞ ∞
D (X)= ∫ x 2 f (x) dx − (M (x))2= ∫ x 25 e −5 xdx − 1 =
−∞
= − 2 (
− 5x)
0 25
− 1 =
∫ x d e
∞
0 ∫
dx
1 2 1 1 1
25 5 5 25 25
= x 2 e −5 x |∞ +

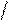 0
0
e −5 x ⋅ 2 xdx − = 0 + ⋅ − =
 σ(X) =
σ(X) =
D (x)=
1 25 = 1 5
Ответ:
M (x) = 1 5;
D (x) = 1 25;
σ(x)
= 1 5.
Закон распределения –
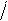
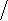
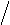 показательный, с параметром λ = 5.
показательный, с параметром λ = 5.
Пример 2. Найти вероятность попадания в заданный интервал (0,6)
нормально
 распределенной случайной величины X, если ее математическое ожидание среднее квадратичное отклонение σ = 2
распределенной случайной величины X, если ее математическое ожидание среднее квадратичное отклонение σ = 2
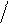 Решение: Известно, что
Решение: Известно, что
m = 4 и
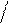 P (a < X < b)= Ф ((b − m)
P (a < X < b)= Ф ((b − m)
поэтому
σ)− Ф ((a − m)
σ),
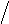
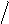 P (0 < X < 6)= Ф ((6 − 4)
P (0 < X < 6)= Ф ((6 − 4)
2)− Ф ((0 − 4)
2)= Ф (1)− Ф (−2)=
Ф (1)+ Ф (2)= 0,3413 + 0, 4772 = 0,8185
Ответ: 0,8185.
Задачи 721 – 730
721) Вероятность попадания при каждом выстреле
p = 0.8. Имеется три снаряда.
Написать закон распределения случайной величины X - числа израсходованных снарядов, если стрельба ведется до первого попадания в цель. Найти математическое ожидание M (X) этой случайной величины.
722) Найти математическое ожидание и дисперсию числа появления события A в
трех независимых испытаниях, если в одном испытании событие A происходит с вероятностью 0, 4.
723) Стрелок производит по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,3. Определить закон распределения случайной величины X числа попадания в мишень при трех выстрелах и найти ее математическое ожидание M (X).
724) В урне имеется 4 шара с номерами от 1 до 4. Вынули 2 шара. Случайная
величина X - сумма номеров этих шаров. Найти закон распределения
случайной величины X и ее математическое ожидание M (X).
725) Найти математическое ожидание
M (X)
и дисперсию
D (X)
непрерывной
случайной величины X, если интегральная функция
F (x) = 0
при
x < 0,
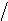 F (x) = x 5
F (x) = x 5
при 0 ≤ x < 5, и
F (x) = 1
при
x ≥ 5. Как называется закон
распределения такой случайной величины?
726) Найти математическое ожидание M (X)
и среднее квадратическое отклонение
σ(x)
непрерывной случайной величины X, если плотность
f (x) = 0
при
x < 0 и
f (x) = 2 e −2 x
при
x > 0. Как называется закон распределения такой
случайной величины?
727) Найти математическое ожидание
M (X)
и дисперсию
D (X)
непрерывной
случайной величины X, если интегральная функция
F (x) = 0
при
x < 0,
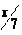 F (x) = при 0 ≤ x < 7, и
F (x) = при 0 ≤ x < 7, и
F (x) = 1
при
x ≥ 7. Как называется закон
распределения такой случайной величины?
728) Найти математическое ожидание
M (X)
и среднее квадратическое
отклонение
σ(x)
непрерывной случайной величины X, если плотность
f (x) = 0
при
x < 0, и
f (x) = 3 e −3 x
при
x > 0. Как называется закон
распределения такой случайной величины?
729) Найти математическое ожидание
M (X)
и дисперсию
D (X)
непрерывной
случайной величины X, если интегральная функция
F (x) = 0
при
x < 0,
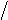 F (x) = x
F (x) = x
9 при 0 <
x < 9, и
F (x) = 1 при
x > 9. Как называется закон
распределения такой случайной величины?
730) Найти математическое ожидание
M (X)
и среднее квадратическое
отклонение
σ(x)
непрерывной случайной величины X, если плотность
f (x) = 0
при
x < 0, и
f (x) = 4 e −4 x
при
x > 0. Как называется закон
распределения такой случайной величины?
Задачи 731 – 740
В следующих задачах требуется найти вероятность попадания в заданный интервал
(a, b) нормально распределенной случайной величины X, если известны ее математическое ожидание m и среднее квадратичное отклонение ó.
| 731)
| a
| =1,
| b = 3,
| m = 1,
| ó = 2,
|
| 732)
| a
| =3,
| b = 7,
| m = 2,
| ó = 1,
|
| 733)
| a
| =3,
| b = 7,
| m = 3,
| ó = 1,
|
| 734)
| a
| =0,
| b = 8,
| m = 0,
| ó = 4,
|
| 735)
| a
| =1,
| b = 9,
| m = 1,
| ó = 2,
|
| 736)
| a
| =6,
| b = 9,
| m = 6,
| ó = 1,
|
| 737)
| a
| =0,
| b = 9,
| m = 0,
| ó = 3,
|
| 738)
| a
| =5,
| b = 8,
| m = 2,
| ó = 3,
|
| 739)
| a
| =5,
| b = 9,
| m = 5,
| ó = 3,
|
| 740)
| a
| =8,
| b = 9,
| m = 7,
| ó = 1.
|







 12 12 144
12 12 144






 12 12 12 12 72
12 12 12 12 72 P (A)= m,
P (A)= m, 144
144 ; б).
; б).


 P (A ⋅ B)= P (A)⋅ P (B | A)= 7
P (A ⋅ B)= P (A)⋅ P (B | A)= 7


 .
.





 P (A H 1) = 0,5;
P (A H 1) = 0,5; P (A H 3) = 0,05
P (A H 3) = 0,05
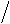
 x > 0.
x > 0.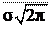 Если закон распределения известен, появляется возможность вычислить все
Если закон распределения известен, появляется возможность вычислить все
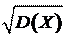 3. Среднее квадратическое отклонение σ(X) =.
3. Среднее квадратическое отклонение σ(X) =. так называемую функцию Лапласа Ф (x)
так называемую функцию Лапласа Ф (x) P (a < X < b)= Ф ((b − m)
P (a < X < b)= Ф ((b − m)


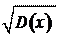
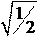 σ(X) = = ≈ 0,707
σ(X) = = ≈ 0,707 = − xe −5 x ∞
= − xe −5 x ∞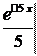
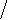 e −5 xdx = 0 − = 1 5
e −5 xdx = 0 − = 1 5 − xe −5 x ∞ = lim x = lim 1 = 0
− xe −5 x ∞ = lim x = lim 1 = 0




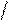 0
0 σ(X) =
σ(X) =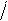
 показательный, с параметром λ = 5.
показательный, с параметром λ = 5. распределенной случайной величины X, если ее математическое ожидание среднее квадратичное отклонение σ = 2
распределенной случайной величины X, если ее математическое ожидание среднее квадратичное отклонение σ = 2 Решение: Известно, что
Решение: Известно, что P (a < X < b)= Ф ((b − m)
P (a < X < b)= Ф ((b − m)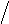
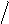 P (0 < X < 6)= Ф ((6 − 4)
P (0 < X < 6)= Ф ((6 − 4)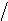 F (x) = x 5
F (x) = x 5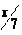 F (x) = при 0 ≤ x < 7, и
F (x) = при 0 ≤ x < 7, и F (x) = x
F (x) = x


