1. Делимость. Все показатели производственно-технологического процесса могут быть увеличены или уменьшены при сохранении их взаимной пропорциональности.
2. Аддитивность. Полное количество каждого из потребленных ресурсов равняется сумме одноименных ресурсов, затраченных при реализации всех применявшихся технологических процессов.
Применительно к фиксированному производственно-технологическому процессу приведенные условия означают, что доходы строго пропорциональны затраченным ресурсам, а непропорциональный эффект (технологического или экономического характера) оказывается невозможным.
При решении задач условной оптимизации целесообразно использовать методы безусловной оптимизации, учитывая большое количество разработанных по этим методам программ. С этой целью задача условной оптимизации сводится к задаче безусловной оптимизации устранением ограничений путем преобразования параметра XI, на значения которого наложены ограничения, в неограничиваемый.
Сведение исходной задачи условной оптимизации к последовательности задач безусловной оптимизации может быть выполнено с помощью функций штрафа.
Метод отжига - метод поисковой оптимизации, в котором для увеличения вероятности выхода из областей притяжения локальных минимумов допускается переход в точки с худшим значением целевой функции с некоторой вероятностью
Метод распространения ограничений - метод решения задач условной оптимизации, основанный на сокращении интервалов значений управляемых переменных (или мощности множеств значений этих переменных) благодаря учету исходных ограничений. Сокращенные интервалы в явном виде определяют подмножество допустимых решений
Различают методы условной и безусловной оптимизации по наличию или отсутствию ограничений. Для реальных задач характерно наличие ограничений, однако методы безусловной оптимизации также представляют интерес, поскольку задачи условной оптимизации с помощью специальных методов могут быть сведены к задачам без ограничений.
Суть метода заключается в преобразовании задачи условной оптимизации в задачу безусловной оптимизации с помощью образования новой целевой функции.
Для решения задач данного типа применяются такие методы как:
1) Симплекс-метод,разработанный Danzig'oM около 50 лет назад, перебирает "базисные" решения, построенные путем фиксирования достаточного количества переменных, чтобы матрица системы ограничений Ах = b стала квадратной. Такая полученная система может быть решена для единственных значений оставшихся переменных. Базисные решения являются экстремальными граничными точками области допустимых решений, определяемой системой ограничений, и симплекс-метод может рассматриваться как прохождение от одной такой точки к другой по границе области.
Метод барьеров или внутренних точек,с другой стороны, обходит точки из внутренней части области допустимых значений. Эта группа методов происходит от технологий нелинейного программирования, разработанных и популяризованных в 60-х гг. Fiacco и McCormick, но их приложения к линейному программированию датируются только 1984 г.
Родственная ЛП задача целочисленного программирования(или целочисленного линейного программирования, точнее говоря) допускает только целочисленные значения переменных. Задачи ЦП обычно ближе к реальным задачам, чем задачи ЛП, но намного более трудоемки в решении. Наиболее широко используемые методы решения задач ЦП используют решение серии задач ЛП, чтобы найти целочисленные решения и доказать оптимальность. Поэтому большая часть ПО ЦП построена на базе ПО ЛП, и данный FAQ применим для решения задач этих двух видов.
Линейное и целочисленное программирование пригодно для моделирования множества различных проблем в планировании, маршрутизации, разработке расписаний, назначениях и дизайне. ЛП и его расширения используются в транспортной индустрии, энергетике и машиностроении.
В жизни решение задач оптимизации занимает очень много времени и это достаточно трудоемкий процесс, где необходимо учесть все параметры. И чтобы облегчить нам работу по поиску оптимума программисты разных стран написали большое количество программ для решения задач оптимизации практически во всех отраслях производства и сферах нашей жизни.
Система Mathematica объединяет в себе запас мировых математических знаний, накопленных в справочной литературе, и использует свои собственные
революционные алгоритмы, чтобы развивать эти знания.
Умение проводить аналитические расчеты — одно из главных достоинств этой программы, автоматизирующей математические расчеты. Mathematica умеет преобразовывать и упрощать алгебраические выражения, дифференцировать и вычислять определенные и неопределенные интегралы, вычислять конечные и бесконечные суммы и произведения, решать алгебраические и дифференциальные уравнения и системы, а также разлагать функции в ряды и находить пределы
Mathematica позволяет строить двух и трехмерные графики различных типов в виде точек и линии на плоскости, поверхностей, а также контурные, градиентные (dencity plot), параметрические. Mathematica выполняет построение графика в три этапа. На первом создается множество графических примитивов, на втором они преобразуются в независимое от вычислительной платформы описание на языке PostScript, а на третьем это описание переводится в графический формат для той системы, на которой установлена Mathematica.
Система MatLab
Данная система ориентирована на матричные и векторные вычисления (её названием является сокращение словосочетания Matrix Laboratory) и предназначена в основном для численного моделирования технических систем. Её последние версии содержат элементы универсальных систем компьютерной алгебры: специальный модуль MatLab Notebook, позволяющий, в том числе, использовать возможности Microsoft Word для оформления документов, а также приобретённый у компании Maple Waterloo модуль основной символьной библиотеки системы Maple V 4.0 для выполнения некоторых аналитических расчётов. Входной язык в определённой мере напоминает BASIC (с элементами Фортрана и Паскаля). Интерфейс менее доступный и красочный, чем у системы MathCAD, однако скорость вычислений выше.
Использование в образовании нецелесообразно; система предназначена для профессиональной работы в области математики и смежных областях.
Система MatLab предназначена для выполнения инженерных и научных расчетов и высококачественной визуализации получаемых результатов. Эта система применяется в математике, вычислительном эксперименте, имитационном моделировании.
В пакет входит множество хорошо проверенных численных методов (решателей), операторы графического представления результатов, средства создания диалогов. Отличительной особенностью MatLab по сравнению с обычными языками программирования является матричное представление данных и большие возможности матричных операций над данными. Используя пакет MatLab можно, как из кубиков конструктора, построить довольно сложную математическую модель, или написать свою программу (весьма похожую на Фортран-программу). А можно используя SIMULINK и технологию визуального моделирования составить имитационную модель или систему автоматического регулирования.
Гибкий язык MatLab дает возможность инженерам и ученым легко реализовывать свои идеи. Мощные численные методы и графические возможности позволяют проверять предположения и новые возникающие идеи, а интегрированная среда дает возможность быстро получать практические результаты.
Вопрос 5. Формулирование задачи нелинейного программирования в общем виде. Способы решения задачи нелинейного программирования (метод ньютона и т.д.).
В общем виде задача нелинейного программирования (ЗНП) формируется следующим образом:
f (x1, x2,..., xn) max (min)
ì gi (x1, x2 ..., xn £ bi, i=1, m1
ï gi (x1, x2 ..., xn ³ bi, i=m1+1, m2
í...........................
î gi (x1, x2 ..., xn = bi, i=m2+1, m2
где xj - управляющие переменные или решения ЗНП, j=1, n;
bi - фиксированные параметры, i=1, m;
f, gi, i=1, n - заданные функции от n переменных.
Если f и gi линейны, то ) проходит в задачу линейного программирования.
Решить задачу нелинейного программирования - это значит найти такие значения управляющих переменных xj, j=1, n, которые удовлетворяют системе ограничений и доставляют максимум или минимум функции f.
Для задачи нелинейного программирования, в отличие от линейных задач, нет единого решения. В зависимости от вида целевой функции и ограничений разработано несколько специальных методов решения, к которым относятся методы множителей Лагранжа, квадратичное и выпуклое программирование, градиентные методы, ряд приближенных методов решения, графический метод. Заметим, что нелинейное моделирование экономических задач часто бывает довольно искусственным. Большая часть экономических проблем сводится к линейным моделям.
Одним из методов, которые позволяют свести задачу нелинейного программирования к решению системы уравнений является метод неопределенных множителей Лагранжа.
Если целевая функция F является линейной, а ограниченным пространством является политоп, то задача является задачей линейного программирования, которая может быть решена с помощью хорошо известных решений линейного программирования.
Если целевая функция является вогнутой (задача максимизации), или выпуклой (задача минимизации) и множество ограничений является выпуклой, то задачу называют выпуклой и в большинстве случаев могут быть использованы общие методы выпуклой оптимизации.
Если целевая функция является отношением вогнутых и выпуклых функций (при максимизации) и ограничения выпуклые, то задача может быть преобразована в задачу выпуклой оптимизации использованием техник дробного программирования.
Существуют несколько методов для решения невыпуклых задач. Один подход заключается в использовании специальных формулировок задач линейного программирования. Другой метод предусматривает использование методов ветвей и границ, где задача делится на подклассы, чтобы быть решенной с выпуклыми (задача минимизации) или линейными аппроксимациями, которые образуют нижнюю границу общей стоимости в пределах раздела. При следующих разделах в определенный момент будет получено фактическое решение, стоимость которого равна лучшей нижней границе, полученной для любого из приближенных решений. Это решение является оптимальным, хотя, возможно, не единственным. Алгоритм можно прекратить на ранней стадии, с уверенностью, что оптимальное решение находится в рамках допустимого отклонения от найденной лучшей точки; такие точки называются (Эпсилон)-оптимальными. Завершение у (Эпсилон)-оптимальных точек, как правило, необходимое для обеспечения конечности завершения. Это особенно полезно для больших, сложных задач и задач с неопределенными расходами или значениями, где неопределенность может быть определена из соответствующей оценки надежности.
Диференцийность и условия регулярности, условия Каруша - Куна - Такера (ККТ) обеспечивают необходимые условия оптимальности решения. При выпуклости, эти условия являются и достаточными.
Метод половинного деления
Для этого метода существенно, чтобы функция f(x) была непрерывна и ограничена в заданном интервале [a, b], внутри которого находится корень. Предполагается также, что значения функции на концах интервала f(a) и f(b) имеют разные знаки, т.е. выполняется условие f(a)f(b) < 0.
Обозначим исходный интервал [a, b] как [a0, b0]. Для нахождения корня уравнения f(x) = 0 отрезок [a0, b0] делится пополам, т.е. вычисляется начальное приближение x0 = (a0 + b0)/2. Если f(x0) = 0, то значение x0 = x* является корнем уравнения. В противном случае выбирается один из отрезков [a0, x0] или [x0, b0], на концах которого функция f(x) имеет разные знаки, так как корень лежит в этой половине. Далее выбранный отрезок обозначается как [a1, b1], вновь делится пополам точкой x1 = (a1 + b1)/2 и т.д. В результате на некоторой итерации получается точный корень x* уравнения f(x) = 0, либо бесконечная последовательность вложенных отрезков [a0, b0], [a1, b1],..., [ai, bi],..., таких, что f(ai)f(bi) < 0 (i =1, 2,...), сходящихся к корню x*.
Если требуется определить корень x* с погрешностью e, то деление исходного интервала [a, b] продолжают до тех пор, пока длина отрезка [ai, bi] не станет меньше 2e, что записывается в форме условия
çbi - ai ç< 2e.
В этом случае середина последнего интервала [ai, bi] с требуемой степенью точности дает приближенное значение корня
x*» (ai + bi) / 2.
Метод половинного деления легко реализуется на ЭВМ и является наиболее универсальным среди итерационных методов уточнения корней. Его применение гарантирует получение решения для любой непрерывной функции f(x), если найден интервал, на котором она изменяет знак. В том случае, когда корни не отделены, будет найден один из корней уравнения. Метод всегда сходится, но скорость сходимости является небольшой, так как за одну итерацию точность увеличивается примерно в два раза. Поэтому на практике метод половинного деления обычно применяется для грубого нахождения корней уравнения, поскольку при повышении требуемой точности значительно возрастает объем вычислений.
3. Метод хорд
Пусть дано уравнение f(x) = 0, где f(x) - непрерывная функция, имеющая в интервале (a, b) производные первого и второго порядков. Корень считается отделенным и находится на отрезке [a, b].
Идея метода хорд состоит в том, что на достаточно малом промежутке [a, b] дугу кривой y = f(x) можно заменить хордой и в качестве приближенного значения корня принять точку пересечения с осью абсцисс. Рассмотрим случай (рис. 1), когда первая и вторая производные имеют одинаковые знаки, т.е. f '(x)f ²(x) > 0. Тогда уравнение хорды, проходящей через точки A0 и B, имеет вид
 .
.
Приближение корня x = x1, для которого y = 0, определяется как
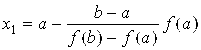 .
.
Аналогично для хорды, проходящей через точки A1 и B, вычисляется следующее приближение корня
 .
.
В общем случае формула метода хорд имеет вид:
 . (2)
. (2)
Если первая и вторая производные имеют разные знаки, т.е.
f '(x)f "(x) < 0,
то все приближения к корню x* выполняются со стороны правой границы отрезка [a, b], как это показано на рис. 2, и вычисляются по формуле:
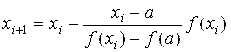 . (3)
. (3)
Выбор формулы в каждом конкретном случае зависит от вида функции f(x) и осуществляется по правилу: неподвижной является граница отрезка [a, b] изоляции корня, для которой знак функции совпадает со знаком второй производной. Формула (2) используется в том случае, когда f(b)f "(b) > 0. Если справедливо неравенство f(a)f "(a) > 0, то целесообразно применять формулу (3).
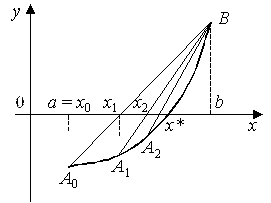
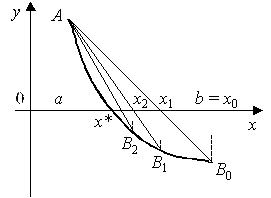
Рис. 1 Рис. 2
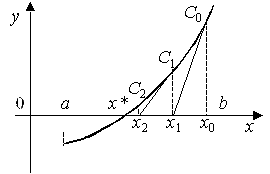

Рис. 3 Рис. 4
Итерационный процесс метода хорд продолжается до тех пор, пока не будет получен приближенный корень с заданной степенью точности. При оценке погрешности приближения можно пользоваться соотношением:
 .
.
Тогда условие завершения вычислений записывается в виде:
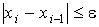 , (4)
, (4)
где e - заданная погрешность вычислений. Необходимо отметить, что при отыскании корня метод хорд нередко обеспечивает более быструю сходимость, чем метод половинного деления.
4. Метод Ньютона (касательных)
Пусть уравнение (1) имеет корень на отрезке [a, b], причем f '(x) и f "(x) непрерывны и сохраняют постоянные знаки на всем интервале [a, b].
Геометрический смысл метода Ньютона состоит в том, что дуга кривой y = f(x) заменяется касательной. Для этого выбирается некоторое начальное приближение корня x0 на интервале [a, b] и проводится касательная в точке C0(x0, f(x0)) к кривой y = f(x) до пересечения с осью абсцисс (рис. 3). Уравнение касательной в точке C0 имеет вид
y = f(x0) + f '(x0)×(x - x0).
Далее за приближение корня принимается абсцисса x1, для которой y = 0:

Затем проводится касательная через новую точку C1(x1, f(x1)) и определяется точка x2 ее пересечения с осью 0x и т.д. В общем случае формула метода касательных имеет вид:

В результате вычислений получается последовательность приближенных значений x1, x2,..., xi,..., каждый последующий член которой ближе к корню x*, чем предыдущий. Итерационный процесс обычно прекращается при выполнении условия (4).
Начальное приближение x0 должно удовлетворять условию:
f(x0) f ¢¢(x0) > 0. (6)
В противном случае сходимость метода Ньютона не гарантируется, так как касательная будет пересекать ось абсцисс в точке, не принадлежащей отрезку [a, b]. На практике в качестве начального приближения корня x0, обычно выбирается одна из границ интервала [a, b], т.е. x0 = a или x0 = b, для которой знак функции совпадает со знаком второй производной.
Метод Ньютона обеспечивает высокую скорость сходимости при решении уравнений, для которых значение модуля производной ½f ¢(x)½вблизи корня достаточно велико, т.е. график функции y = f(x) в окрестности корня имеет большую крутизну. Если кривая y = f(x) в интервале [a, b] почти горизонтальна, то применять метод касательных не рекомендуется.
Существенным недостатком рассмотренного метода является необходимость вычисления производных функции для организации итерационного процесса. Если значение f ¢(x) мало изменяется на интервале [a, b], то для упрощения вычислений можно пользоваться формулой
 , (7)
, (7)
т.е. значение производной достаточно вычислить только один раз в начальной точке. Геометрически это означает, что касательные в точках Ci(xi, f(xi)), где i = 1, 2,..., заменяется прямыми, параллельными касательной, проведенной к кривой y = f(x) в начальной точке C0(x0, f(x0)), как это показано на рис. 4.
В заключение необходимо отметить, что все изложенное справедливо в том случае, когда начальное приближение x0 выбрано достаточно близким к истинному корню x* уравнения. Однако это не всегда просто осуществимо. Поэтому метод Ньютона часто используется на завершающей стадии решения уравнений после работы какого-либо надежно сходящегося алгоритма, например, метода половинного деления.
5. Метод простой итерации
Чтобы применить этот метод для решения уравнения (1) необходимо преобразовать его к виду 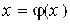 . Далее выбирается начальное приближение
. Далее выбирается начальное приближение 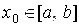 и вычисляется x1, затем x2 и т.д.:
и вычисляется x1, затем x2 и т.д.:
x1 = j(x0); x2 = j(x1); …; xk = j(xk-1);...
нелинейный алгебраический уравнение корень
Полученная последовательность сходится к корню при выполнении следующих условий:
1) функция j(x) дифференцируема на интервале [a, b].
2) во всех точках этого интервала j¢(x) удовлетворяет неравенству:
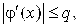 0 £ q £ 1. (8)
0 £ q £ 1. (8)
При таких условиях скорость сходимости является линейной, а итерации следует выполнять до тех пор, пока не станет справедливым условие:
 .
.
Критерий вида
 ,
,
может использоваться только при 0 £ q £ ½. Иначе итерации заканчиваются преждевременно, не обеспечивая заданную точность. Если вычисление q затруднительно, то можно использовать критерий окончания вида
 ;
;  .
.
Возможны различные способы преобразования уравнения (1) к виду 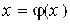 . Следует выбирать такой, который удовлетворяет условию (8), что порождает сходящийся итерационный процесс, как, например, это показано на рис. 5, 6. В противном случае, в частности, итерационный процесс расходится и не позволяет получить решение (рис. 7).
. Следует выбирать такой, который удовлетворяет условию (8), что порождает сходящийся итерационный процесс, как, например, это показано на рис. 5, 6. В противном случае, в частности, итерационный процесс расходится и не позволяет получить решение (рис. 7).

Рис. 5

Рис. 6

В MS Excel существует возможность с помощью надстройки Поиск решения найти решение, оптимальное в некотором смысле при нескольких входных значениях и наборе ограничений на решение.
Диспетчер сценариев способен запомнить несколько решений, найденных данным средством и сгенерировать на этой основе отчет.
С помощью надстройки Поиск решенияможно решать как линейные задачи (задачи линейного, целочисленного и стохастического программирования), так и нелинейные (задачи нелинейного программирования).
Работа по решению некоторой оптимизационной задачи всегда начинается с построения математической модели.



 .
.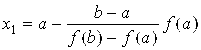 .
. .
. . (2)
. (2)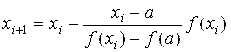 . (3)
. (3)



 .
.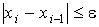 , (4)
, (4)

 , (7)
, (7)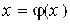 . Далее выбирается начальное приближение
. Далее выбирается начальное приближение 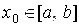 и вычисляется x1, затем x2 и т.д.:
и вычисляется x1, затем x2 и т.д.: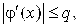 0 £ q £ 1. (8)
0 £ q £ 1. (8) .
. ,
, ;
;  .
.




