Теорема 6. Если функция f (x) интегрируема на отрезке  , то она интегрируема на любом отрезке
, то она интегрируема на любом отрезке  .
.
□ Пусть ε > 0 произвольное число. Поскольку f (x) интегрируема на  , то существует разбиение Т, такое что
, то существует разбиение Т, такое что
 (10)
(10)
Если  разбиение
разбиение  , получено по разбиению Т добавлением точек
, получено по разбиению Т добавлением точек 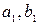 , а
, а  - разбиение
- разбиение  образованное точками разбиения
образованное точками разбиения  , принадлежащему отрезку
, принадлежащему отрезку  . Тогда
. Тогда
 .
.
Оценки верны, поскольку в последнем неравенстве первая сумма содержит неотрицательные слагаемые, соответствующие разбиению  , а вторая – слагаемые, соответствующие разбиению
, а вторая – слагаемые, соответствующие разбиению  , причем каждое слагаемое первой суммы входит во вторую сумму. Действительно, поскольку
, причем каждое слагаемое первой суммы входит во вторую сумму. Действительно, поскольку  , в силу (10) и свойства 2 сумм Дарбу имеем:
, в силу (10) и свойства 2 сумм Дарбу имеем:
 .
.
Тогда по критерию интегрируемости, f (x) интегрируема на  . ■
. ■
Теорема 7. Пусть  . Тогда, если f (x)интегрируема на отрезках
. Тогда, если f (x)интегрируема на отрезках  и
и  , то она интегрируема на отрезке
, то она интегрируема на отрезке 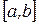 , причем
, причем
 (11)
(11)
□ Пусть  , Т - разбиение
, Т - разбиение  , образованное точками разбиений
, образованное точками разбиений 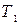 и
и 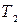 отрезков
отрезков  и
и  . По критерию интегрируемости разбиения
. По критерию интегрируемости разбиения 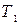 и
и 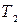 можно выбрать так, чтобы
можно выбрать так, чтобы
 и
и  .
.
Очевидно, что  и, следовательно,функция интегрируема по критерию интегрируемости.
и, следовательно,функция интегрируема по критерию интегрируемости.
Теперь докажем (11). Интегральную сумму для построенного разбиения Т можно записать  .
.
Переходя здесь к пределу при 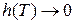 (при этом
(при этом  ,
,  ), получим доказываемое равенство (11). ■
), получим доказываемое равенство (11). ■
Формула (11) остается справедливой, если на отрезок [ a,b ] разбит на большее, чем два отрезка. Эта теорема называется свойством аддитивности определенного интеграла.
Теорема 8. Если f (x) и g (x) интегрируемы на отрезке  , тогда их сумма также интегрируема на
, тогда их сумма также интегрируема на  и справедливо равенство:
и справедливо равенство:
 . (12)
. (12)
□ 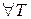 отрезка
отрезка  и при любом выборе точек
и при любом выборе точек  имеем
имеем
 .
.
В силу интегрируемости f(x) и g(x) существуют пределы интегральных сумм, стоящих в правой части, поэтому существует и предел левой части при h (Т) → 0 и по определению определенного интеграла получим (12). ■
Теорема 9. Пусть f (x) интегрируема на  и А - постоянная. Тогда функция Аf (x) также интегрируема на отрезке
и А - постоянная. Тогда функция Аf (x) также интегрируема на отрезке  , причем
, причем
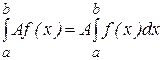 .
.
□ Доказательство следует из равенств:
 . ■
. ■
Теорема 10. Пусть функции f (x) и g (x) определены на  , причем f (x) интегрируема на
, причем f (x) интегрируема на  , а g (x) отличается от f (x) в конечном числе точек. Тогда справедливо равенство:
, а g (x) отличается от f (x) в конечном числе точек. Тогда справедливо равенство:
 .
.
□ Рассмотрим функцию  . Очевидно
. Очевидно  на
на  за исключением конечного числа точек, которые обозначим
за исключением конечного числа точек, которые обозначим  . Положим
. Положим  . Пусть Т - разбиение. Тогда каждая из точек
. Пусть Т - разбиение. Тогда каждая из точек  принадлежит не более, чем двум отрезкам
принадлежит не более, чем двум отрезкам  (
( ) одновременно, а на остальных отрезках
) одновременно, а на остальных отрезках  , то для любого разбиения Т отрезка
, то для любого разбиения Т отрезка  , при любом выборе точек
, при любом выборе точек  имеем:
имеем:  .
.
Переходя в этом неравенстве к пределу при h (Т) → 0 получим:
 .
.
В силу Т.8 функция 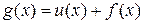 интегрируема на
интегрируема на  и
и
 . ■
. ■
Замечание. Определенный интеграл можно определить и для функций, заданных всюду на отрезке  , за исключением конечного числа точек этого отрезка. Если доопределить функцию в этих точках произвольным образом, мы получим функцию, интегрируемую по Риману. В силу теоремы, интеграл не зависит от того какое значение принимает подынтегральная функция в этих точках.
, за исключением конечного числа точек этого отрезка. Если доопределить функцию в этих точках произвольным образом, мы получим функцию, интегрируемую по Риману. В силу теоремы, интеграл не зависит от того какое значение принимает подынтегральная функция в этих точках.
Теорема 11. Если функции f (x) и g (x)интегрируемы на  , то их произведение также интегрируемо на отрезке
, то их произведение также интегрируемо на отрезке  .
.
□ Без доказательства.
Теорема 12. Если функция f (x)интегрируема на  и
и 
 , то
, то
 . (13) □ Т.к.
. (13) □ Т.к. 
 , то
, то  отрезка
отрезка  и при любом выборе
и при любом выборе 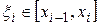 будет справедливо неравенство
будет справедливо неравенство  . Переходя к пределу h (T)
. Переходя к пределу h (T) 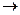 0 получим (13). ■
0 получим (13). ■
Следствие. Если 
 и функции интегрируемы, то
и функции интегрируемы, то  .
.
Теорема 13. Если f (x) интегрируема на отрезке  , то
, то  также интегрируема на
также интегрируема на  и выполняется неравенство:
и выполняется неравенство:
 .
.
□ Из неравенства  следует, что колебание функции
следует, что колебание функции 
 на отрезке
на отрезке 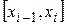 не меньше колебания
не меньше колебания  функции
функции  на этом же отрезке, т.е.
на этом же отрезке, т.е.  . Т.к. f (x) интегрируема, то
. Т.к. f (x) интегрируема, то  . Тогда для разбиения Т получим
. Тогда для разбиения Т получим  , т.е.
, т.е.  интегрируемая. Пусть теперь Т - произвольное разбиение отрезка
интегрируемая. Пусть теперь Т - произвольное разбиение отрезка  , тогда,по свойству абсолютной величины имеем:
, тогда,по свойству абсолютной величины имеем:

 .
.
Переходя к пределу h (T) 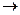 0получим (13), в силу теоремы сравнения для пределов. ■
0получим (13), в силу теоремы сравнения для пределов. ■
Замечание. Из интегрируемости  на
на  не следует интегрируемость f (x). Например, функция
не следует интегрируемость f (x). Например, функция  , где
, где  - функция Дирихле, не является интегрируемой на
- функция Дирихле, не является интегрируемой на  т.к.
т.к.  не интегрируется, а функция
не интегрируется, а функция  интегрируемая.
интегрируемая.
Tеорема14. Если  и функция f (x)интегрируема на
и функция f (x)интегрируема на  , то
, то 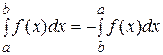 , если
, если  , то
, то  .
.
□ Пусть Т некоторое разбиение  . Обозначим
. Обозначим
 .
.
Тогда
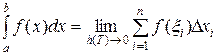 ;
;
 -
-  . ■
. ■
Классы функций, интегрируемых по Риману. Выясним, какие функции можно интегрировать по Риману.
Теорема 15. Непрерывная на отрезке  функция f (x) интегрируема по Риману на этом отрезке.
функция f (x) интегрируема по Риману на этом отрезке.
□ В силу теоремы Кантора, непрерывная на отрезке  функция равномерно непрерывна па этом отрезке, т.е.
функция равномерно непрерывна па этом отрезке, т.е.  , что на любом отрезке
, что на любом отрезке  , для которого
, для которого 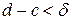 , колебание будет удовлетворять неравенству:
, колебание будет удовлетворять неравенству:
 <
<  .
.
Пусть Т разбиение отрезка  с шагом
с шагом  . Тогда колебание на
. Тогда колебание на 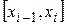 удовлетворяет неравенству
удовлетворяет неравенству
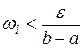 .
.
Для этого разбиения имеем
 .
.
Тогда согласно критерию интегрируемости функция f(x) интегрируема по Риману на  . ■
. ■
Теорема 16. Ограниченная на отрезке  функция f (x), имеющая на
функция f (x), имеющая на  конечное число точек разрыва интегрируема на этом отрезке.
конечное число точек разрыва интегрируема на этом отрезке.
□ Вначале рассмотрим случай, когда f (x) имеет единственную точку разрыва, причем точкой разрыва является один из концов отрезка. Пусть это точка а. Обозначим  колебание f (x)на
колебание f (x)на  . Зададим произвольное положительное число ε. Выберем точку x 1, чтобы
. Зададим произвольное положительное число ε. Выберем точку x 1, чтобы  .
.
На отрезке  функция непрерывна и следовательно интегрируема по Риману. По критерию интегрируемости найдется такое разбиение
функция непрерывна и следовательно интегрируема по Риману. По критерию интегрируемости найдется такое разбиение  отрезка
отрезка  , что
, что  . Для разбиения
. Для разбиения  отрезка
отрезка  в силу предыдущего, получим
в силу предыдущего, получим
 .
.
По критерию интегрируемости это означает, что f (x) интегрируема на  . Аналогично, если точка разрыва при
. Аналогично, если точка разрыва при  . Рассмотрим общий случай. Пусть
. Рассмотрим общий случай. Пусть  точки разрыва f (x) на (a,b). Выберем точки
точки разрыва f (x) на (a,b). Выберем точки 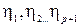 , так чтобы выполнялось неравенства
, так чтобы выполнялось неравенства
 . На каждом из отрезков
. На каждом из отрезков  функция интегрируема в силу предыдущего рассуждения, т.к. имеет не более одной точки разрыва. Тогда она интегрируема по Риману и на всем отрезке
функция интегрируема в силу предыдущего рассуждения, т.к. имеет не более одной точки разрыва. Тогда она интегрируема по Риману и на всем отрезке  в силу свойства аддитивности. ■
в силу свойства аддитивности. ■
Функция f (x) называется кусочно-непрерывной наотрезке  если она имеет на этом отрезке не более конечного числа точек разрыва 1-го рода. Тогда теорема может быть сформулирована так: кусочно-непрерывная на отрезке функция f (x)интегрируема на нем.
если она имеет на этом отрезке не более конечного числа точек разрыва 1-го рода. Тогда теорема может быть сформулирована так: кусочно-непрерывная на отрезке функция f (x)интегрируема на нем.
Теорема 17. Монотонная на отрезке  функция f (x) интегрируема по Риману на этом отрезке.
функция f (x) интегрируема по Риману на этом отрезке.
□ Для определенности будем считать, что f (x) не убывает. Зададим произвольное  . Пусть Т - разбиение
. Пусть Т - разбиение  с шагом
с шагом  . Очевидно, что в силу монотонности
. Очевидно, что в силу монотонности  . Поэтому, проверяя критерий интегрируемости, получаем
. Поэтому, проверяя критерий интегрируемости, получаем
 . ■
. ■
Теорема 18. Ограниченная на отрезке  функция f (x), имеющая счетное множество точек разрыва, интегрируема по Риману на этом отрезке.
функция f (x), имеющая счетное множество точек разрыва, интегрируема по Риману на этом отрезке.
□ Без доказательства.
Таким образом, интегрируемыми по Риману функциями являются следующие функции: непрерывные; ограниченные с конечным числом точек разрыва; монотонные; ограниченные, имеющие счетное множество точек.
Теоремы о среднем для интеграла Римана. Имеют место важные для оценок интегралов теоремы.
Теорема19. Пусть выполняется условия:
1) функции f (x)и g (x) интегрируемы на отрезке  ;
;
2)  ;
;
3)  ;
;
тогда справедлива формула
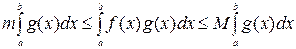 (14)
(14)
□ Произведение  интегрируемо на
интегрируемо на  по теореме 11. Тогда, интегрируя почленно неравенство
по теореме 11. Тогда, интегрируя почленно неравенство  , получим формулу. ■
, получим формулу. ■
Следствие. При условиях теоремы, если  , справедлива формула:
, справедлива формула:
 .
.
Теорема 20 ( обобщенная теорема о среднем ). Пусть выполняются условия
1) функция f (x) непрерывная на отрезке  ;
;
2) g (x)интегрируема на  ;
;
3)  .
.
Тогда  , что справедлива формула среднего значения:
, что справедлива формула среднего значения:
 (15)
(15)
□ Поскольку функции  интегрируемы на отрезке
интегрируемы на отрезке  , то справедливы неравенства (14). Если
, то справедливы неравенства (14). Если  , то из (14) следует, что
, то из (14) следует, что  и формула (15) будет выполняться
и формула (15) будет выполняться  . Пусть
. Пусть 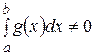 , тогда из (14) получим:
, тогда из (14) получим:
 .
.
Так как f (x) непрерывна на  , то по второй теореме Вейерштрасса
, то по второй теореме Вейерштрасса 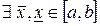 , такие, что
, такие, что  . Тогда
. Тогда
 .
.
В силу теоремы Коши для непрерывных на отрезке функций, непрерывная функция f(x) принимает все промежуточные значения между m и M. Поэтому существует точка
ξ є [ a, b ], в которой будет выполнятся равенство:
 .
.
Откуда следует формула (15). ■
Следствие (теорема о среднем). Если f (x) непрерывна на [ a, b ], то существует ξ є [ a, b ], такая, что
 .
.
Очевидно, что формула следует из (15) при g (x) ≡ 1.
Значение  - называется средним значением
- называется средним значением  на[ a, b ].
на[ a, b ].
Замечание. Если f (x) не является непрерывной, то формула (15) в общем случае несправедлива. Действительно, пусть
 ;
; 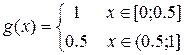 ;
;

 ;
; 
Однако точки ξ є [0,1], где f ( ) = 2/3 не существует.
) = 2/3 не существует.



 , то она интегрируема на любом отрезке
, то она интегрируема на любом отрезке  .
. (10)
(10) разбиение
разбиение 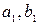 , а
, а  - разбиение
- разбиение  образованное точками разбиения
образованное точками разбиения  , принадлежащему отрезку
, принадлежащему отрезку  . Тогда
. Тогда .
. , причем каждое слагаемое первой суммы входит во вторую сумму. Действительно, поскольку
, причем каждое слагаемое первой суммы входит во вторую сумму. Действительно, поскольку  , в силу (10) и свойства 2 сумм Дарбу имеем:
, в силу (10) и свойства 2 сумм Дарбу имеем: .
. . Тогда, если f (x)интегрируема на отрезках
. Тогда, если f (x)интегрируема на отрезках  и
и  , то она интегрируема на отрезке
, то она интегрируема на отрезке 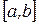 , причем
, причем (11)
(11) , Т - разбиение
, Т - разбиение 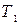 и
и 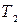 отрезков
отрезков  и
и  и
и  .
. и, следовательно,функция интегрируема по критерию интегрируемости.
и, следовательно,функция интегрируема по критерию интегрируемости. .
.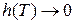 (при этом
(при этом  ,
,  ), получим доказываемое равенство (11). ■
), получим доказываемое равенство (11). ■ . (12)
. (12)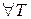 отрезка
отрезка  имеем
имеем .
.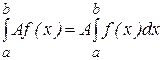 .
. . ■
. ■ .
. . Очевидно
. Очевидно  на
на  . Положим
. Положим  . Пусть Т - разбиение. Тогда каждая из точек
. Пусть Т - разбиение. Тогда каждая из точек  (
( ) одновременно, а на остальных отрезках
) одновременно, а на остальных отрезках  .
. .
.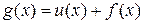 интегрируема на
интегрируема на  . ■
. ■
 , то
, то . (13) □ Т.к.
. (13) □ Т.к.  отрезка
отрезка  и при любом выборе
и при любом выборе 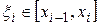 будет справедливо неравенство
будет справедливо неравенство  . Переходя к пределу h (T)
. Переходя к пределу h (T)  0 получим (13). ■
0 получим (13). ■
 и функции интегрируемы, то
и функции интегрируемы, то  .
. также интегрируема на
также интегрируема на  .
. следует, что колебание функции
следует, что колебание функции 
 на отрезке
на отрезке 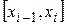 не меньше колебания
не меньше колебания  . Т.к. f (x) интегрируема, то
. Т.к. f (x) интегрируема, то  . Тогда для разбиения Т получим
. Тогда для разбиения Т получим  , т.е.
, т.е. 
 .
. на
на  , где
, где  - функция Дирихле, не является интегрируемой на
- функция Дирихле, не является интегрируемой на  интегрируемая.
интегрируемая. и функция f (x)интегрируема на
и функция f (x)интегрируема на 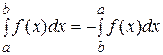 , если
, если  , то
, то  .
. .
.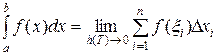 ;
; -
-  . ■
. ■ , что на любом отрезке
, что на любом отрезке  , для которого
, для которого 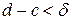 , колебание будет удовлетворять неравенству:
, колебание будет удовлетворять неравенству: <
<  .
. . Тогда колебание на
. Тогда колебание на 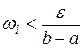 .
. .
. колебание f (x)на
колебание f (x)на  . Зададим произвольное положительное число ε. Выберем точку x 1, чтобы
. Зададим произвольное положительное число ε. Выберем точку x 1, чтобы  .
. функция непрерывна и следовательно интегрируема по Риману. По критерию интегрируемости найдется такое разбиение
функция непрерывна и следовательно интегрируема по Риману. По критерию интегрируемости найдется такое разбиение  отрезка
отрезка  . Для разбиения
. Для разбиения  отрезка
отрезка  .
. . Рассмотрим общий случай. Пусть
. Рассмотрим общий случай. Пусть  точки разрыва f (x) на (a,b). Выберем точки
точки разрыва f (x) на (a,b). Выберем точки 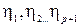 , так чтобы выполнялось неравенства
, так чтобы выполнялось неравенства . На каждом из отрезков
. На каждом из отрезков  функция интегрируема в силу предыдущего рассуждения, т.к. имеет не более одной точки разрыва. Тогда она интегрируема по Риману и на всем отрезке
функция интегрируема в силу предыдущего рассуждения, т.к. имеет не более одной точки разрыва. Тогда она интегрируема по Риману и на всем отрезке  . Пусть Т - разбиение
. Пусть Т - разбиение  . Очевидно, что в силу монотонности
. Очевидно, что в силу монотонности  . Поэтому, проверяя критерий интегрируемости, получаем
. Поэтому, проверяя критерий интегрируемости, получаем . ■
. ■ ;
; ;
;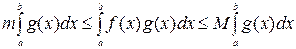 (14)
(14) интегрируемо на
интегрируемо на  , получим формулу. ■
, получим формулу. ■ , справедлива формула:
, справедлива формула: .
. .
. , что справедлива формула среднего значения:
, что справедлива формула среднего значения: (15)
(15) интегрируемы на отрезке
интегрируемы на отрезке  , то из (14) следует, что
, то из (14) следует, что  и формула (15) будет выполняться
и формула (15) будет выполняться  . Пусть
. Пусть 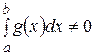 , тогда из (14) получим:
, тогда из (14) получим: .
.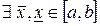 , такие, что
, такие, что  . Тогда
. Тогда .
. .
. .
. - называется средним значением
- называется средним значением  на[ a, b ].
на[ a, b ]. ;
; 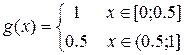 ;
;
 ;
; 
 ) = 2/3 не существует.
) = 2/3 не существует.