Для определения интервала, содержащего точку минимума, обычно используют следующую процедуру.
Выбирают две стартовые точки x и у такие, что y=x+s.
Затем, если f(x)>f(y), определяют следующие точки xk+1 = xk + s до тех пор, пока не будет получено f(xk) < f(xk+1).
В этом случае полученный интервал [x, xk+1] "накрывает" искомую точку минимума.
Если же f(x) < f(y), то выбирается противоположное направление. Точки строятся по правилу xk+1= xk- s до тех пор, пока не будет получено f(xk) < f(xk+1).
Основной проблемой при применении описанной процедуры является правильный выбор величины s. Во многих прикладных задачах переменная изменяется в пределах многих степеней десятки (например, от 0,001 до 10000). Тогда при неправильном выборе величины s минимизация может потребовать слишком больших затрат (при очень малом s - на "накрытие" точки минимума, а при большом - на последующее за "накрытием" сужение отрезка до требуемой точности).
Для того чтобы преодолеть эту проблему, был предложен подход с удвоением шага. В этом случае определение верхней границы интервала осуществляется по правилу
xk+1= x0+ 2ks.
После того, как точка минимума была накрыта, нижняя граница интервала определяется тем же самым процессом, но с изменением знака перед s и в обратном направлении.
И последнее, что следует здесь учесть - это возможность того, что целевая функция вообще является постоянной. Для учета этого обстоятельства необходимо вводить максимальную длину шага, которая не должна быть превышена в процессе определения отрезка, содержащего точку минимума.
Методы прямого поиска. (деления интервала)
Иногда такой процесс используют не только для "накрытия" точки минимума, но и для ее отыскания. Будем считать функцию f(x) унимодальной на отрезке [a, b].
Шаблонный подход: равномерно распределить точки в пределах начального интервала. При этом длина интервала, гарантированно накрывающего точку минимума, 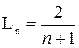 .
.
Дихотомия (метод половинного деления). Исходный отрезок делится пополам парой измерений: 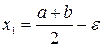 ,
, 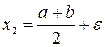 , где ε – некоторое заранее заданное достаточно малое число. Вычисляются значения функции в этих точках и сравниваются между собой. Если при поиске минимума
, где ε – некоторое заранее заданное достаточно малое число. Вычисляются значения функции в этих точках и сравниваются между собой. Если при поиске минимума 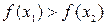 , то отрезок [a; x1] заведомо не содержит точку минимуиа и поэтому интервал поиска можно сократить, перенеся его левый конец в точку х2. После этого возникает та же, что и ранее, задача, но интервал поиска сокращен (с точностью до ε) вдвое. Таким образом осуществляется последовательное деление исходного интервала пополам парами измерений. При этом
, то отрезок [a; x1] заведомо не содержит точку минимуиа и поэтому интервал поиска можно сократить, перенеся его левый конец в точку х2. После этого возникает та же, что и ранее, задача, но интервал поиска сокращен (с точностью до ε) вдвое. Таким образом осуществляется последовательное деление исходного интервала пополам парами измерений. При этом 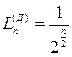 .
.
Дихотомия существенно эффективнее, чем шаблонный подход. Так, для сужения интервала в 100 раз нужно 198 пассивных измерений или 14 дихотомий.
Метод Фибоначчи. (число Фибоначчи равно сумме двух предыдущих 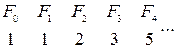 ). Недостаток метода Фибоначчи – необходимость заранее знать число шагов n.
). Недостаток метода Фибоначчи – необходимость заранее знать число шагов n. 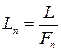 ,
, 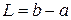 .
.
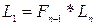 .
.
На первом шаге симметрично относительно краев интервала строятся точки на расстоянии 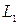 ,
, 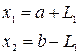 . Вычисляются значения функций в этих точках и сравниваются. Аналогично методу Дихотомии производится сужение интервала.
. Вычисляются значения функций в этих точках и сравниваются. Аналогично методу Дихотомии производится сужение интервала.
На втором и последующих шагах делается только одно измерение 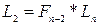 , …,
, …, 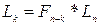 ,
, 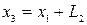 , если
, если 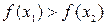 и
и 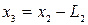 , если
, если 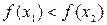 . И так далее, до тех пор пока интервал неопределенности не будет меньше ε. В качестве точки минимума выбирается середина отрезка.
. И так далее, до тех пор пока интервал неопределенности не будет меньше ε. В качестве точки минимума выбирается середина отрезка.
Для сокращения интервала в 100 раз требуется всего 11 измерений.
Метод золотого сечения. Принципиальная характеристика метода: симметрия измерений относительно концов интервала. 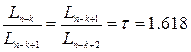 . Первое измерение выбирается так, чтобы
. Первое измерение выбирается так, чтобы 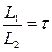 , второе измерение проводится симметрично первому. Дальнейшие действия проводятся как в методе Фибоначчи. Таким образом после проведения очередного измерения, на чинная со второго, интервал сокращается в 1,618 раз.
, второе измерение проводится симметрично первому. Дальнейшие действия проводятся как в методе Фибоначчи. Таким образом после проведения очередного измерения, на чинная со второго, интервал сокращается в 1,618 раз.
Поиск методом "золотого сечения" является предельным случаем поиска Фибоначчи и при достаточно больших n дает результат, лишь на 17% худший. Зато не требует начального задания количества вычислений функции.
Метод Монте-Карло работает аналогично Фибоначчи и «золотому сечению» положение разбиения же выбирается случайным образом. Прост в реализации, результаты в среднем близки к «золотому сечению».



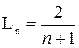 .
.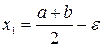 ,
, 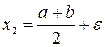 , где ε – некоторое заранее заданное достаточно малое число. Вычисляются значения функции в этих точках и сравниваются между собой. Если при поиске минимума
, где ε – некоторое заранее заданное достаточно малое число. Вычисляются значения функции в этих точках и сравниваются между собой. Если при поиске минимума 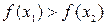 , то отрезок [a; x1] заведомо не содержит точку минимуиа и поэтому интервал поиска можно сократить, перенеся его левый конец в точку х2. После этого возникает та же, что и ранее, задача, но интервал поиска сокращен (с точностью до ε) вдвое. Таким образом осуществляется последовательное деление исходного интервала пополам парами измерений. При этом
, то отрезок [a; x1] заведомо не содержит точку минимуиа и поэтому интервал поиска можно сократить, перенеся его левый конец в точку х2. После этого возникает та же, что и ранее, задача, но интервал поиска сокращен (с точностью до ε) вдвое. Таким образом осуществляется последовательное деление исходного интервала пополам парами измерений. При этом 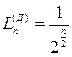 .
.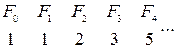 ). Недостаток метода Фибоначчи – необходимость заранее знать число шагов n.
). Недостаток метода Фибоначчи – необходимость заранее знать число шагов n. 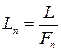 ,
, 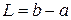 .
.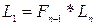 .
.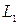 ,
, 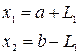 . Вычисляются значения функций в этих точках и сравниваются. Аналогично методу Дихотомии производится сужение интервала.
. Вычисляются значения функций в этих точках и сравниваются. Аналогично методу Дихотомии производится сужение интервала.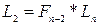 , …,
, …, 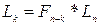 ,
, 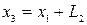 , если
, если 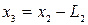 , если
, если 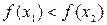 . И так далее, до тех пор пока интервал неопределенности не будет меньше ε. В качестве точки минимума выбирается середина отрезка.
. И так далее, до тех пор пока интервал неопределенности не будет меньше ε. В качестве точки минимума выбирается середина отрезка.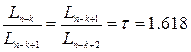 . Первое измерение выбирается так, чтобы
. Первое измерение выбирается так, чтобы 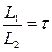 , второе измерение проводится симметрично первому. Дальнейшие действия проводятся как в методе Фибоначчи. Таким образом после проведения очередного измерения, на чинная со второго, интервал сокращается в 1,618 раз.
, второе измерение проводится симметрично первому. Дальнейшие действия проводятся как в методе Фибоначчи. Таким образом после проведения очередного измерения, на чинная со второго, интервал сокращается в 1,618 раз.


