Лабораторная работа № 6
Цель работы: лабораторной работы – ознакомить студентов с возможностями использования пакета Mathcad для решения кратных интегралов, привить навыки работы с компьютером в процессе изучения дисциплины «Компьютерные исчисления», навыки самостоятельной работы с современными математическими программами.
Указания к выполнению лабораторной работы:
Подобно тому, как задача о нахождении площади криволинейной трапеции, а также ряд задач механики и в, частности, задача о нахождении работы, совершаемой переменной силой по перемещению материальной точки вдоль отрезка прямой, привели к понятию определённого интеграла, так и более сложные задачи геометрии и физики (нахождение объёма тела, площади криволинейной поверхности, массы тела, статических моментов и моментов инерции тел и др.) приводят к понятию кратных интегралов.
Вычисления двойных и тройных интегралов вызывают некоторые трудности у студентов (как правило, расстановка пределов интегрирования в повторных интегралах). Использование компьютерной техники, программного продукта Mathcad позволяет производить достаточно громоздкие вычисления, связанные с непосредственным вычислением интегралов и строить графики функций, ограничивающих область интегрирования, что существенно повышает наглядность и способствует более глубокому пониманию изучаемых теоретических положений. В пятой и шестой лабораторных работах рассмотрены элементы теории поля, т. е.
решается ряд задач, связанных со скалярными и векторными полями.
Отчёт по лабораторной работе должен включать выполнение индивидуального задания и ответы на вопросы.
Задание 1. Вычислить двойной интеграл по указанной области G.
Задание 2: Найти площадь фигуры, ограниченной данными линиями.
Задание 3. Вычислить координаты центра тяжести пластины.
Задание 4. Тело V задано ограничивающими его поверхностями,  - плотность. Найти объем тела.
- плотность. Найти объем тела.
Задание 5. Покажите, что поле 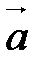 является потенциальным, и найдите потенциал этого поля. НЕ НУЖНО ДЕЛАТЬ!!!
является потенциальным, и найдите потенциал этого поля. НЕ НУЖНО ДЕЛАТЬ!!!
Теоретические положения
Двойной интеграл
Пусть функция f(x, y) = f(P) определена и непрерывна на замкнутой ограниченной области G плоскости O xy,  – некоторое разбиение области на элементарные подобласти
– некоторое разбиение области на элементарные подобласти  , площади которых также обозначим через
, площади которых также обозначим через  , а диаметры – через dk. Зафиксируем точки Pk Î
, а диаметры – через dk. Зафиксируем точки Pk Î  , k=1, 2, …n. Выражение
, k=1, 2, …n. Выражение

называется интегральной суммой для функции f(P) по области G.
Определение. Если существует предел последовательности интегральных сумм Sn при 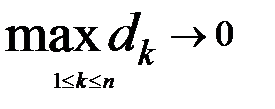 (при этом n ®¥) и если этот предел не зависит ни от способа разбиения области G на элементарные подобласти
(при этом n ®¥) и если этот предел не зависит ни от способа разбиения области G на элементарные подобласти  , ни от выбора точек Pk Î
, ни от выбора точек Pk Î  .
.
.
Таким образом,
 .
.
Для двойного интеграла справедливы свойства линейности и аддитивности:
а) линейность:
 ;
;
б) аддитивность: если G = G1+G2, то
 .
.
Вычисление двойного интеграла сводится к вычислению повторных интегралов следующим образом. Пусть область G (рис. 6.1) ограничена кривыми  ,
, 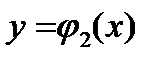 , x=a, x=b причём всюду на [ a, b ] функции
, x=a, x=b причём всюду на [ a, b ] функции 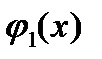 и
и  непрерывны и
непрерывны и 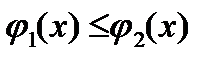 . Тогда
. Тогда
 ,
,
причём сначала вычисляется внутренний интеграл по переменной y (x считается постоянной), потом полученный результат интегрируется по x. Интегралы такого вида называются повторными. Если кривая 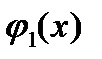 (или кривая
(или кривая 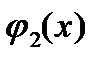 ) в промежутке
) в промежутке  задаётся различными аналитическими выражениями, то следует разбить область интегрирования на части и воспользоваться свойством аддитивности интеграла.
задаётся различными аналитическими выражениями, то следует разбить область интегрирования на части и воспользоваться свойством аддитивности интеграла.
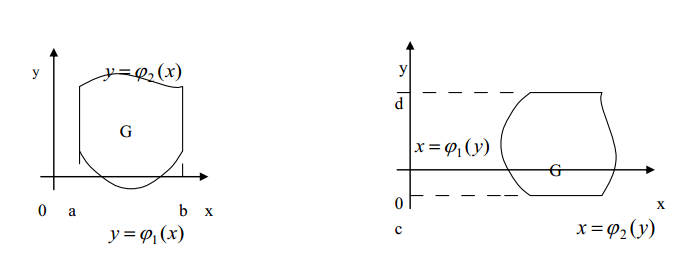
Рис.6.1 Рис. 6.2
Аналогично, можно построить второй повторный интеграл. Если область G ограничена кривыми  ,
,  , y=c, y=d, причём всюду на [c, d] функции
, y=c, y=d, причём всюду на [c, d] функции  и
и  непрерывны и
непрерывны и  (рис. 6.2), то
(рис. 6.2), то
 .
.
Векторное поле
Векторным полем называется часть пространства, каждой точке которого поставлен в соответствие вектор  :
:
 .
.
Векторными линиями векторного поля  называются такие линии, которые в каждой своей точке М имеют направление
называются такие линии, которые в каждой своей точке М имеют направление  . Они определяются системой дифференциальных уравнений
. Они определяются системой дифференциальных уравнений
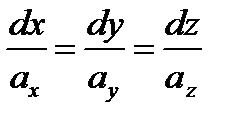 .
.
Если поле а – силовое поле, то работа А п оля при перемещении материальной точки по дуге L равна
 .
.
Циркуляция векторного поля  по замкнутому контуру С в выбранном направлении равна
по замкнутому контуру С в выбранном направлении равна
 .
.
Потоком векторного поля через поверхность S в сторону, определяемую единичным вектором нормали  к поверхности S, называется интеграл
к поверхности S, называется интеграл

 .
.
Дивергенцией векторного поля  в точке M 0 называется скалярная величина
в точке M 0 называется скалярная величина  , равная отнесённому к единице объёма потоку вектора
, равная отнесённому к единице объёма потоку вектора  через поверхность бесконечно малого объёма, окружающего данную точку:
через поверхность бесконечно малого объёма, окружающего данную точку:
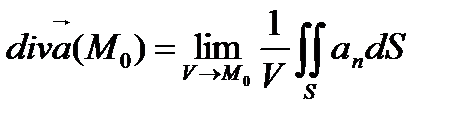 .
.
В декартовых координатах дивергенция вычисляется по формуле
 .
.
Ротором (вихрем) векторного поля  в точке M 0 называется вектор, проекция которого на любое направление
в точке M 0 называется вектор, проекция которого на любое направление  определяется равенством
определяется равенством
 ,
,
где S – площадь площадки, перпендикулярной  , ограниченной замкнутым контуром C. Контур С пробегается против часовой стрелки, если смотреть на него из конца вектора
, ограниченной замкнутым контуром C. Контур С пробегается против часовой стрелки, если смотреть на него из конца вектора  .
.
В декартовых координатах:
 .
.
Формула Стокса. Циркуляция векторного поля  по замкнутому контуру С равна потоку его ротора через произвольную поверхность S, «натянутую» на контур С:
по замкнутому контуру С равна потоку его ротора через произвольную поверхность S, «натянутую» на контур С:
 .
.
где направление  нормали к поверхности S согласовано с направлением обхода контура С.
нормали к поверхности S согласовано с направлением обхода контура С.
Вектор  , являющийся градиентом некоторого скалярного поля φ называется потенциальным вектором, а поле вектора
, являющийся градиентом некоторого скалярного поля φ называется потенциальным вектором, а поле вектора  называется потенциальным полем, скалярная функция φ называется потенциалом векторного поля.
называется потенциальным полем, скалярная функция φ называется потенциалом векторного поля.
Для потенциальности поля  , заданного в односвязной области, необходимо и достаточно, чтобы оно было безвихревым, т.е. чтобы
, заданного в односвязной области, необходимо и достаточно, чтобы оно было безвихревым, т.е. чтобы  . В этом случае существует потенциал φ, определяемый как решение уравнения
. В этом случае существует потенциал φ, определяемый как решение уравнения
 .
.
С точностью до постоянной он находится по формуле
 ,
,
где интеграл берётся по любому пути, исходящему из некоторой фиксированной точки M 0, где поле существует. Обычно в качестве пути выбирают ломаную, звенья которой параллельны координатным осям, например, ломаную M 0 M 1 M 2 M (рис. 6.5), а φ (M 0) полагают равной С (С=const). Тогда

 .
.

Рис. 6.5
Кратные интегралы
Кратным называется интеграл функции многих переменных, берущийся по нескольким переменным. Для того чтобы вычислить кратный интеграл:
1. Введите, как обычно, оператор интегрирования.
2. В соответствующих местозаполнителях введите имя первой переменной интегрирования и пределы интегрирования по этой переменной.
3. На месте ввода подынтегральной функции введите ещё один оператор интегрирования (рис. 6.6).
4. Точно так же введите вторую переменную, пределы интегрирования и подынтегральную функцию (если интеграл двукратный) или следующий оператор интегрирования (если более чем двукратный) и т. д., пока выражение с многократным интегралом не будет введено окончательно.

Рис. 6.6. Ввод нескольких операторов интегрирования для расчёта кратного интеграла
Пример символьного и численного расчёта двукратного интеграла в бесконечных пределах приведён в листинге 6.1. Обратите внимание, что символьный процессор "угадывает" точное значение интеграла л, а вычислительный определяет его приближённо и выдаёт в виде числа 3.142.
Листинг 6.1. Символьное и численное вычисления кратного интеграла:

Внимание!
Аккуратнее вводите в редакторе Mathcad кратные интегралы, если они имеют различные пределы интегрирования по разным переменным. Не перепутайте пределы, относящиеся к разным переменным. Если вы имеете дело с такого рода задачами, обязательно разберитесь с листингом 6.2, в котором символьный процессор вычисляет двукратный интеграл. В первой строке пределы интегрирования [а,b] относятся к переменной у, а во второй строке – к переменной X.
Листинг 6.2. Символьное вычисление кратных интегралов:

Указания к выполнению лабораторной работы:
Задание 1: Вычислить двойной интеграл  по указанной области G.
по указанной области G.
Порядок выполнения задания 1
1. Определите подынтегральную функцию как функцию переменных x и y.
2. Определите кривые, задающие область интегрирования.
3. Постройте на одном графике линии, ограничивающие область интегрирования.
4. Найдите границы области интегрирования и точки пересечения графиков
данных функций.
5. Вычислите аналитически искомый интеграл.
6. Вычислите двойной интеграл, изменяя порядок интегрирования.
Пример 1. Расставить пределы интегрирования двумя способами и вычислить
двойной интеграл  , если область интегрирования G ограничена линиями у=х,
, если область интегрирования G ограничена линиями у=х,  , х=2.
, х=2.
Образец выполнения задания в Mathcad
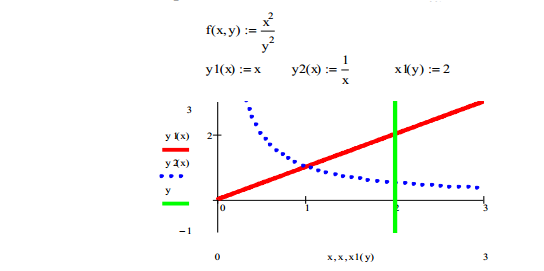
Найдём точки пересечения графиков функций. Для этого надо решить систему
уравнений

Система имеет два решения, но исходя из графика видно, что подходит точка с координатами (1,1). а – x- вая координата точки. Ещё две точки имеют координаты (2, y1(2)), (2, y2(2)). Найдём другое выражение для границ области интегрирования - это функции x2(y), x3(y).

Вычислим двойной интеграл, переходя к повторному двумя способами.


Рис 6.7 – Решение задания 1.
Таблица 6.1
Варианты задания1
| №№
| f(x,y)
| Уравнения линий, ограничивающих область G
|
|
| 
| 
|
|
| 
| 
|
|
| 
| 
|
|
| 
| 
|
|
| 
| 
|
|
| 
| 
|
|
| 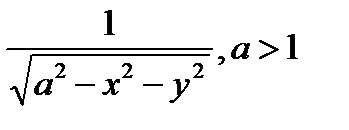
| 
|
|
| 
| 
|
|
| 
| 
|
|
| 
| 
|
|
| 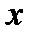
| 
|
|
| 
| 
|
|
| 
| 
|
|
| 
| 
|
|
| 
| 
|
|
| 
| 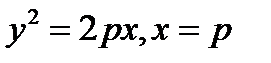
|
|
| 
| 
|
|
| 
| 
|
|
| 
| 
|
|
| 
| 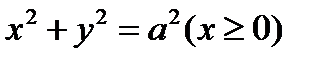
|
|
| 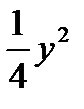
| 
|
|
| 
| 
|
|
| 
| 
|
|
| 
| 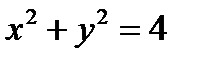
|
|
| 
| 
|
|
| 
| 
|
|
| 
| 
|
|
| 
| 
|
|
| 
| 
|
|
| 
| 
|
Задание 2: Найти площадь фигуры, ограниченной данными линиями.
Порядок выполнения задания 2
1. Введите полярные координаты.
2. Определите в полярных координатах уравнение кривых, ограничивающих данную область.
3. Изобразите на графике область интегрирования.
4. Вычислите площадь полученной фигуры, используя полярные координаты.
Вариант 1-12. Рассмотрите двойной интеграл  где D: y = x + m,
где D: y = x + m,
y = x + n, y = p x + r, y = p x + t.
Таблица 6. 3
| N
| m
| n
| p
| t
| r
| N
| m
| n
| p
| t
| r
|
| 1.
|
| -4
| -1/4
|
|
| 7.
|
| -9
| -1/9
| 13/9
|
|
| 2.
|
| -5
| -1/5
| 9/5
|
| 8.
|
| -10
| -1/10
| 7/5
|
|
| 3.
|
| -6
| -1/6
| 5/3
|
| 9.
| -1
|
| -1
|
|
|
| 4.
|
| -7
| -1/7
| 11/7
|
| 10.
|
| -11
| -1/11
| 15/11
|
|
| 5.
|
| -2
| -1/2
|
|
| 11.
| -2
| -1
| -2
|
|
|
| 6.
|
| -8
| -1/8
| 3/2
|
| 12.
| -3
| -2
| -3
|
|
|
Вариант 12-24. Рассмотрите двойной интеграл  D: y = x2 - m,
D: y = x2 - m,
y = x2 - n, y = - x2 + r, y = -x2 + t, x>0.
Таблица 6. 4
| N
| m
| n
| t
| r
| N
| m
| n
| t
| r
|
| 13.
|
|
|
|
| 19.
|
|
|
|
|
| 14.
|
|
|
|
| 20.
|
|
|
|
|
| 15.
|
|
|
|
| 21.
|
|
|
|
|
| 16.
|
|
|
|
| 22.
|
|
|
|
|
| 17.
|
|
| -1
|
| 23.
|
|
|
|
|
| 18.
|
|
| -2
|
| 24.
|
|
|
|
|
Задание 3. Вычислить координаты центра тяжести пластины.
Порядок выполнения задания 2
1 Записать уравнения кривых, которые описывают область D пластины.
2 Найти точки их пересечения, для того чтобы использовать их в двукратном интегрировании.
3 Найти площадь S однородной пластинки через двойной интеграл.
3.1 Обратиться на панели Символы к функции simplify.
3.2 Ввести оператор интегрирования. В соответствующих местах заполнить имя первой переменной и границы интегрирования.
3.3 На месте ввода функции под интегралом ввести ещё один оператор интегрирования, границы интегрирования и подынтегральную функцию

4 Найти аналогично статические моменты Mx и My пластины относительно осей Ох и Оу как двойные интегралы

5 Определить координаты центра тяжести как отношение подынтегральной функции, которая определяет статические моменты пластины относительно осей Ох и Оу


Пример 3. Вычислить координаты центра тяжести пластины площадь которой ограничена линиями x=4y-y 2 и x+y=6.
Образец выполнения задания в Mathcad:
Найти координаты точек пересечения заданных линий, для чего необходимо решить систему уравнений (одной из встроенных функций MathCad, графически или решить систему уравнений).
x=4y-y2
x+y=6.
В результате будут получены точки пересечения А(4;2) и В(3;3).
Записать формулу для вычисления площади через кратный интеграл и использовать на панели Символы функцию simplify
 .
.
Вычислить координаты центра тяжести пластины, которая ограничена кривыми y2=4x+4 и y2=-2x+4.
Площадь

Статические моменты относительно осей Ох и Оу
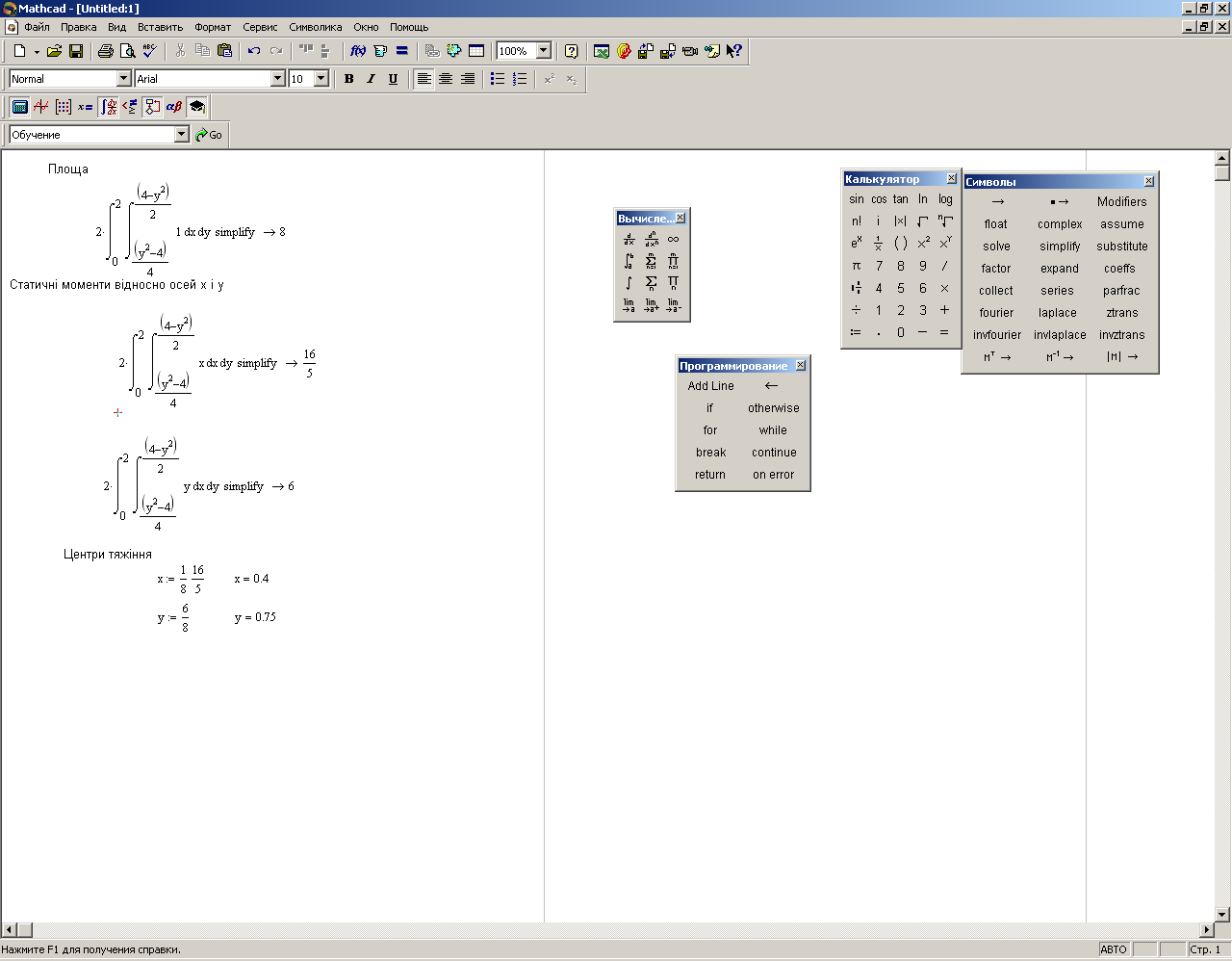

Координаты центра тяжести


Рис 6.9 – Решение задания 3
Таблица 6.5
Варианты задания 3
| Номер варианта
| Функции для вычисления площади фигуры
| Функции для вычисления координат центра тяжести фигуры
|
|
|
|
|
|
| x=y2-2y; x+y=0
| 
|
|
| y=2-x; y2=4x+4
| y=x2; y=2x2; x=1;x=2
|
|
| y2=4x-4; y2=2x (извне параболы)
|
y2=x; x2=y
|
|
| 3y2=25x; 5x2=9y
| y= 
|
|
| y2+2y-3x+1=0; 3x-3y-7=0
| 
|
|
| y=4x-4x2; y=x2-5x
| 
|
|
| x=4-y2; x+2y-4=0
| 
|
|
| y2=4(x-1); x2+ y2=4 (извне параболы)
| 
|
|
| x=y2-2y; x+y=0
| 
|
|
| y=2-x; y2=4x+4
| 
|
|
| y2+2y-3x+1=0; 3x-3y-7=0
| 
|
|
| y=4x-4x2; y=x2-5x
|
y2=x; x2=y
|
|
| x=4-y2; x+2y-4=0
| y= 
|
|
| x=y2-2y; x+y=0
| 
|
|
| y=2-x; y2=4x+4
| y=x2; y=2x2; x=1;x=2
|
|
| y2+2y-3x+1=0; 3x-3y-7=0
| 
|
|
| y=4x-4x2; y=x2-5x
| 
|
|
| x=4-y2; x+2y-4=0
| 
|
|
| x=y2-2y; x+y=0
| 
|
|
| y=2-x; y2=4x+4
| 
|
|
| y2=4(x-1); x2+ y2=4 (извне параболы)
| 
|
|
| y=2-x; y2=4x+4
| y=x2; y=2x2; x=1;x=2
|
|
| 2
| 3
|
|
| y2=4x-4; y2=2x (извне параболы)
|
y2=x; x2=y
|
|
| x=y2-2y; x+y=0
| y= 
|
|
| y=2-x; y2=4x+4
| 
|
|
| 3y2=25x; 5x2=9y
| 
|
|
| x=y2-2y; x+y=0
| 
|
|
| y2+2y-3x+1=0; 3x-3y-7=0
| 
|
|
| y=4x-4x2; y=x2-5x
| y=x2; y=2x2; x=1;x=2
|
|
| x=4-y2; x+2y-4=0
| y2=x; x2=y
|
| | | | | |
Задание 4. Тело V задано ограничивающими его поверхностями,  - плотность. Найти объем тела.
- плотность. Найти объем тела.
Порядок выполнения задания 4
1. Задайте пределы интегрирования (переходя к цилиндрическим или сферическим координатам, если это удобно).
2. Выразите уравнение поверхностей в сферических (цилиндрических) координатах.
3. Задайте якобиан преобразования.
4. Определите плотность тела.
5. Введите формулу для вычисления объёма тела и найдите его значение.
Пример выполнения задания:
Пример 4. Переходя к цилиндрическим координатам, вычислить тройной интеграл  , где область Т задана неравенствами
, где область Т задана неравенствами
 ,
,  ,
, 
Образец выполнения задания в Mathcad:

Указание: Переходя в тройном интеграле к цилиндрическим (сферическим) координатам, целесообразно найти пределы интегрирования отдельно, по возможности используя инструменты Mathcad.
Таблица 6.4
Варианты задания 4
| N
| V
| 
|
| 1.
| x 2 + y 2 =1, x 2 + y 2 = 2 z, x = 0, y = 0, z = 0 (x ≥ 0, y ≥ 0)
| 10 x
|
| 2.
| x 2 + y 2 + z 2 =9, x 2 + y 2 = 4 (x 2 + y 2 ≤4), z = 0 (z ≥ 0)
| 2 z
|
| 3.
| x 2 + y 2 + z 2 =1, x 2 + y 2 = 4, x = 0, y = 0, z = 0 (x≥ 0, y≥ 0,
z≥ 0)
| 
|
| 4.
| x 2 + y 2 = z 2, x 2 + y 2 = z, x = 0, y = 0 (x≥ 0, y ≥ 0)
| 32 z
|
| 5.
| x 2 + y 2 = 4, x 2 + y 2 = 4 z, x= 0, y = 0, z = 0 (x≥ 0, y≥ 0)
| 5 y
|
| 6.
| x 2 + y 2 + z 2 =9, x 2 + y 2 = 4 (x 2 + y 2 ≤ 4)
| 
|
| 7.
| 16(x 2 + y 2) = z 2, x 2 + y 2 =1, x = 0, y = 0, z = 0 (x≥ 0, y ≥ 0,
z ≥ 0)
| 5(x 2 + y 2)
|
| 8.
| x 2 + y 2 + z 2 = 4, x 2 + y 2 = 4 z 2, x = 0, y = 0 (x≥ 0, y ≥ 0, z≥ 0)
| 10 z
|
| 9.
| x 2 + y 2 =1, x 2 + y 2 = z, x = 0, y = 0, z = 0 (x≥ 0, y ≥ 0)
| 10 y
|
| 10.
| x 2 + y 2 + z 2 = 4, x 2 + y 2 =1 (x 2 + y 2 ≤1)
| 6 z
|
| 11.
| 9(x 2 + y 2) = z 2, x 2 + y 2 = 4, x = 0, y = 0, z = 0 (x≥ 0, y ≥ 0,
z ≥ 0)
| 
|
| 12.
| x 2 + y 2 + z 2 = 4, x 2 + y 2 =9 z 2 , x = 0, y = 0, z = 0 (x≥ 0, y ≥ 0, z ≥ 0)
| 
|
| 13.
| x 2 + y 2 =1, x 2 + y 2 = 6 z, x = 0, y = 0, z = 0 (x ≥ 0, y ≥0)
| 90 y
|
| 14.
| x 2 + y 2 + z 2 =9, x 2 + y 2 = 4 (x 2 + y 2 ≤ 4), y = 0 (y ≥ 0)
| 
|
| 15.
| 25(x 2 + y 2) = z 2, x 2 + y 2 = 4, x = 0, y = 0, z = 0 (x ≥ 0, y ≥ 0, z ≥0)
| 2(x 2 + y 2)
|
| 16.
| x 2 + y 2 = 4, x 2 + y 2 =8 z, x = 0, y = 0, z = 0 (x ≥ 0, y ≥0)
| 5 x
|
| 17.
| x 2 + y 2 + z 2 =16, x 2 + y 2 = 4 (x 2 + y 2 ≤ 4)
| 2 
|
| 18.
| 36(x 2 + y 2) = z 2, x 2 + y 2 =1, x = 0, z = 0 (x= 0, z = 0)
| 
|
| 19.
| x 2 + y 2 + z 2 =1, x 2 + y 2 = 4 z 2, x = 0, y = 0 (x ≥ 0, y ≥ 0, z ≥ 0)
| 20 z
|
| 20.
| 49(x 2 + y 2) =16 z 2, x 2 + y 2 = 4 z 2, x = 0, y = 0, z = 0 (x ≥ 0,
y ≥ 0, z ≥ 0)
| 20 z
|
| 21.
| 25(x 2 + y 2) = 4 z 2, 5(x 2 + y 2) = 2 z, x = 0, y = 0 (x ≥ 0, y 0)
| 28 xz
|
| 22.
| 25(x 2 + y 2) = z 2, 5(x 2 + y 2) = z, x = 0, y = 0 (x ≥ 0, y ≥ 0)
| 14 yz
|
| 23.
| 16(x 2 + y 2) = z 2, x 2 + y 2 =1, x = 0, z = 0 (x ≥ 0, z ≥ 0)
| 20 z
|
| 24.
| x 2 + y 2 + z 2 =16, x 2 + y 2 =4 (x 2 + y 2 ≤ 4)
| 5 x
|
Лабораторная работа № 6
Цель работы: лабораторной работы – ознакомить студентов с возможностями использования пакета Mathcad для решения кратных интегралов, привить навыки работы с компьютером в процессе изучения дисциплины «Компьютерные исчисления», навыки самостоятельной работы с современными математическими программами.
Указания к выполнению лабораторной работы:
Подобно тому, как задача о нахождении площади криволинейной трапеции, а также ряд задач механики и в, частности, задача о нахождении работы, совершаемой переменной силой по перемещению материальной точки вдоль отрезка прямой, привели к понятию определённого интеграла, так и более сложные задачи геометрии и физики (нахождение объёма тела, площади криволинейной поверхности, массы тела, статических моментов и моментов инерции тел и др.) приводят к понятию кратных интегралов.
Вычисления двойных и тройных интегралов вызывают некоторые трудности у студентов (как правило, расстановка пределов интегрирования в повторных интегралах). Использование компьютерной техники, программного продукта Mathcad позволяет производить достаточно громоздкие вычисления, связанные с непосредственным вычислением интегралов и строить графики функций, ограничивающих область интегрирования, что существенно повышает наглядность и способствует более глубокому пониманию изучаемых теоретических положений. В пятой и шестой лабораторных работах рассмотрены элементы теории поля, т. е.
решается ряд задач, связанных со скалярными и векторными полями.
Отчёт по лабораторной работе должен включать выполнение индивидуального задания и ответы на вопросы.
Задание 1. Вычислить двойной интеграл по указанной области G.
Задание 2: Найти площадь фигуры, ограниченной данными линиями.
Задание 3. Вычислить координаты центра тяжести пластины.
Задание 4. Тело V задано ограничивающими его поверхностями,  - плотность. Найти объем тела.
- плотность. Найти объем тела.
Задание 5. Покажите, что поле 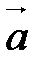 является потенциальным, и найдите потенциал этого поля. НЕ НУЖНО ДЕЛАТЬ!!!
является потенциальным, и найдите потенциал этого поля. НЕ НУЖНО ДЕЛАТЬ!!!
Теоретические положения
Двойной интеграл
Пусть функция f(x, y) = f(P) определена и непрерывна на замкнутой ограниченной области G плоскости O xy,  – некоторое разбиение области на элементарные подобласти
– некоторое разбиение области на элементарные подобласти  , площади которых также обозначим через
, площади которых также обозначим через  , а диаметры – через dk. Зафиксируем точки Pk Î
, а диаметры – через dk. Зафиксируем точки Pk Î  , k=1, 2, …n. Выражение
, k=1, 2, …n. Выражение

называется интегральной суммой для функции f(P) по области G.
Определение. Если существует предел последовательности интегральных сумм Sn при 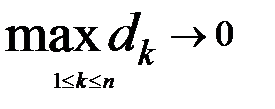 (при этом n ®¥) и если этот предел не зависит ни от способа разбиения области G на элементарные подобласти
(при этом n ®¥) и если этот предел не зависит ни от способа разбиения области G на элементарные подобласти  , ни от выбора точек Pk Î
, ни от выбора точек Pk Î  .
.
.
Таким образом,
 .
.
Для двойного интеграла справедливы свойства линейности и аддитивности:
а) линейность:
 ;
;
б) аддитивность: если G = G1+G2, то
 .
.
Вычисление двойного интеграла сводится к вычислению повторных интегралов следующим образом. Пусть область G (рис. 6.1) ограничена кривыми  ,
, 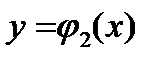 , x=a, x=b причём всюду на [ a, b ] функции
, x=a, x=b причём всюду на [ a, b ] функции 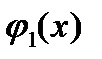 и
и  непрерывны и
непрерывны и 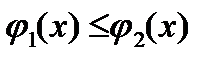 . Тогда
. Тогда
 ,
,
причём сначала вычисляется внутренний интеграл по переменной y (x считается постоянной), потом полученный результат интегрируется по x. Интегралы такого вида называются повторными. Если кривая 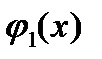 (или кривая
(или кривая 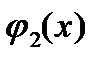 ) в промежутке
) в промежутке  задаётся различными аналитическими выражениями, то следует разбить область интегрирования на части и воспользоваться свойством аддитивности интеграла.
задаётся различными аналитическими выражениями, то следует разбить область интегрирования на части и воспользоваться свойством аддитивности интеграла.
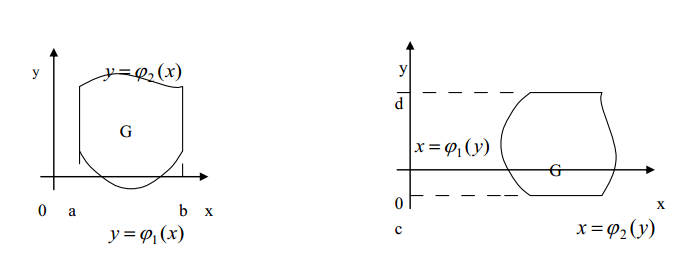
Рис.6.1 Рис. 6.2
Аналогично, можно построить второй повторный интеграл. Если область G ограничена кривыми  ,
,  , y=c, y=d, причём всюду на [c, d] функции
, y=c, y=d, причём всюду на [c, d] функции  и
и  непрерывны и
непрерывны и  (рис. 6.2), то
(рис. 6.2), то
 .
.
Замена переменных в двойных интегралах
Пусть функции
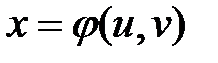 и
и  (1)
(1)
осуществляют взаимно-однозначное непрерывно дифференцируемое отображение области Г плоскости Ouv на область G плоскости Oxy. Это означает, что в области G существует обратное непрерывно дифференцируемое отображение  и
и  в области Г отличен от нуля якобиан преобразования, т.е.
в области Г отличен от нуля якобиан преобразования, т.е.
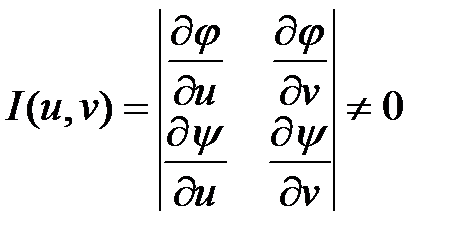 ,
,  . (2)
. (2)
Величины u и v можно рассматривать как прямоугольные координаты для точек области Г и в то же время как криволинейные координаты точек области G.



 - плотность. Найти объем тела.
- плотность. Найти объем тела.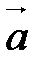 является потенциальным, и найдите потенциал этого поля. НЕ НУЖНО ДЕЛАТЬ!!!
является потенциальным, и найдите потенциал этого поля. НЕ НУЖНО ДЕЛАТЬ!!! – некоторое разбиение области на элементарные подобласти
– некоторое разбиение области на элементарные подобласти  , площади которых также обозначим через
, площади которых также обозначим через  , а диаметры – через dk. Зафиксируем точки Pk Î
, а диаметры – через dk. Зафиксируем точки Pk Î 
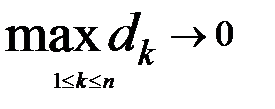 (при этом n ®¥) и если этот предел не зависит ни от способа разбиения области G на элементарные подобласти
(при этом n ®¥) и если этот предел не зависит ни от способа разбиения области G на элементарные подобласти  .
. ;
; .
. ,
, 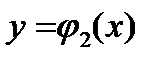 , x=a, x=b причём всюду на [ a, b ] функции
, x=a, x=b причём всюду на [ a, b ] функции 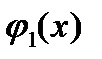 и
и  непрерывны и
непрерывны и 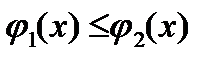 . Тогда
. Тогда ,
,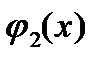 ) в промежутке
) в промежутке  задаётся различными аналитическими выражениями, то следует разбить область интегрирования на части и воспользоваться свойством аддитивности интеграла.
задаётся различными аналитическими выражениями, то следует разбить область интегрирования на части и воспользоваться свойством аддитивности интеграла.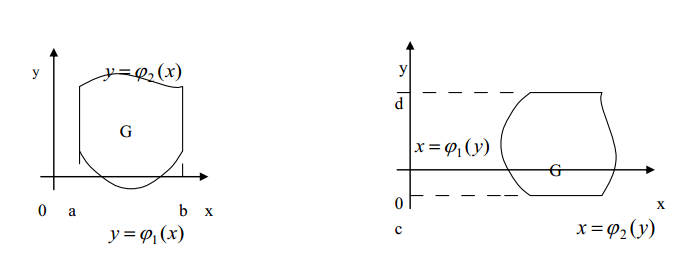
 ,
,  , y=c, y=d, причём всюду на [c, d] функции
, y=c, y=d, причём всюду на [c, d] функции  и
и  непрерывны и
непрерывны и  (рис. 6.2), то
(рис. 6.2), то .
. :
: .
. называются такие линии, которые в каждой своей точке М имеют направление
называются такие линии, которые в каждой своей точке М имеют направление 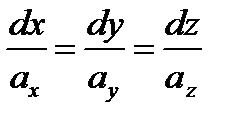 .
. .
. .
. к поверхности S, называется интеграл
к поверхности S, называется интеграл
 .
. , равная отнесённому к единице объёма потоку вектора
, равная отнесённому к единице объёма потоку вектора 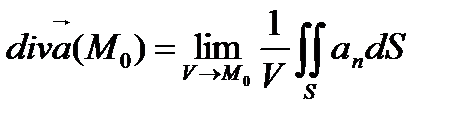 .
. .
.  в точке M 0 называется вектор, проекция которого на любое направление
в точке M 0 называется вектор, проекция которого на любое направление  определяется равенством
определяется равенством ,
, .
. .
. , являющийся градиентом некоторого скалярного поля φ называется потенциальным вектором, а поле вектора
, являющийся градиентом некоторого скалярного поля φ называется потенциальным вектором, а поле вектора  называется потенциальным полем, скалярная функция φ называется потенциалом векторного поля.
называется потенциальным полем, скалярная функция φ называется потенциалом векторного поля. . В этом случае существует потенциал φ, определяемый как решение уравнения
. В этом случае существует потенциал φ, определяемый как решение уравнения .
. ,
,
 .
.



 по указанной области G.
по указанной области G. , если область интегрирования G ограничена линиями у=х,
, если область интегрирования G ограничена линиями у=х,  , х=2.
, х=2.
















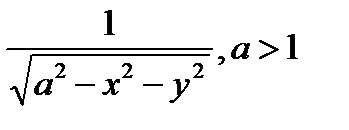







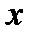










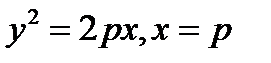







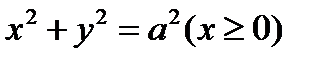
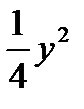






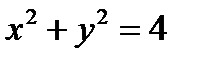












 где D: y = x + m,
где D: y = x + m, D: y = x2 - m,
D: y = x2 - m,



 .
.









 , где область Т задана неравенствами
, где область Т задана неравенствами ,
,  ,
, 







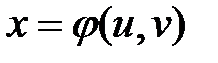 и
и  (1)
(1) и
и  в области Г отличен от нуля якобиан преобразования, т.е.
в области Г отличен от нуля якобиан преобразования, т.е.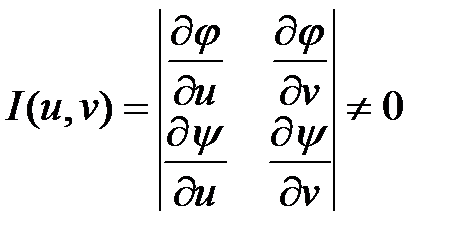 ,
,  . (2)
. (2)


