

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Оснащения врачебно-сестринской бригады.
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Интересное:
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|

1) Уметь составить характеристическое уравнение по виду дифференциального уравнения. Для этого нужно формально заменить  любой буквой в степени n:
любой буквой в степени n:  заменить
заменить  ,
,  заменить
заменить  ,
,  заменить
заменить  .
.
2) Уметь решать квадратное уравнение  по формуле
по формуле
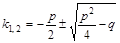
или по теореме Виета  .
.
3) Знать на память вид общего решения в зависимости  .
.
5. Решение неоднородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами основывается на следующей теореме.
Теорема. Если  - некоторое частное решение неоднородного уравнения
- некоторое частное решение неоднородного уравнения  и
и  - общее решение соответствующего однородного уравнения
- общее решение соответствующего однородного уравнения  , то общее решение неоднородного уравнения имеет вид
, то общее решение неоднородного уравнения имеет вид 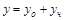 .
.
Правило нахождения частного решения  неоднородного уравнения методом неопределенных коэффициентов.
неоднородного уравнения методом неопределенных коэффициентов.
1. Пусть  , где
, где  - многочлен степени n, тогда:
- многочлен степени n, тогда:
а)  , где
, где  - многочлен той же степени n с неопределенными коэффициентами, если
- многочлен той же степени n с неопределенными коэффициентами, если  и
и  ;
;
б) 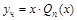 , если
, если  (или
(или  );
);
в)  , если
, если  .
.
2. Пусть 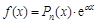 , тогда:
, тогда:
а)  , если
, если  ;
;
б)  , если
, если  (или
(или  );
);
в)  , если
, если  .
.
3. Пусть  , где
, где  и
и  - многочлены, наибольшая степень которых n, тогда:
- многочлены, наибольшая степень которых n, тогда:
а)  , если
, если  ;
;
б)  , если
, если  , где
, где  и
и  - многочлены с неопределенными коэффициентами.
- многочлены с неопределенными коэффициентами.
Пример 1. Найти общее решение уравнения  .
.
▲ Так как функции  и
и  - однородные второго измерения, то данное уравнение – однородное (см. п. 2). Сделаем замену
- однородные второго измерения, то данное уравнение – однородное (см. п. 2). Сделаем замену  . Тогда
. Тогда
 .
.
Предполагая, что  , сокращаем обе части уравнения
, сокращаем обе части уравнения  . Далее имеем:
. Далее имеем:
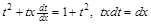 .
.
Разделяя переменные (для разделения переменных необходимо перенести все, что содержит t в одну сторону, а все, что содержит x - в другую, при этом  и
и  должны быть только в числителях), последовательно находим:
должны быть только в числителях), последовательно находим:
 .
.
В последнее выражение вместо переменной t подставим значение  . Получим общий интеграл
. Получим общий интеграл  . Разрешив его относительно y, найдем общее решение исходного дифференциального уравнения:
. Разрешив его относительно y, найдем общее решение исходного дифференциального уравнения:  . ▼
. ▼
|
|
Пример 2. Найти общее решение уравнения  .
.
▲ 1. Убедившись, что данное уравнение линейное (см. п. 2), полагаем
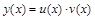 , тогда
, тогда 
и данное уравнение преобразуется к виду
 .
.
Составим систему для определения u и v: 
Решаем первое уравнение системы  (при определении v не нужно писать произвольную постоянную величину, ибо
(при определении v не нужно писать произвольную постоянную величину, ибо  достаточно знать с точностью до постоянной величины). Подставляем во второе уравнение системы
достаточно знать с точностью до постоянной величины). Подставляем во второе уравнение системы  и решаем полученное уравнение:
и решаем полученное уравнение:
 .
.
Зная u и v, находим искомую функцию y:  .
.
2. Перепишем данное уравнение так: 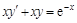 . Рассмотрим однородное уравнение
. Рассмотрим однородное уравнение  . Так как
. Так как  (значение
(значение  не является решением неоднородного уравнения), то
не является решением неоднородного уравнения), то
 -
-
общее решение однородного уравнения.
Применяем далее метод вариации произвольной постоянной C. Общее решение неоднородного уравнения будем искать в виде
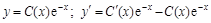 .
.
Подставив значения y и  в неоднородное уравнение, получим
в неоднородное уравнение, получим
 .
.
Т.к. 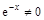 , то
, то  .
.
Подставив это значение  в общее решение неоднородного уравнения, получим
в общее решение неоднородного уравнения, получим 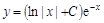 - общее решение неоднородного уравнения. ▼
- общее решение неоднородного уравнения. ▼
Пример 3. Найти общее решение уравнения  .
.
▲ В уравнении нет в явном виде искомой функции y. Понизим порядок этого уравнения, положив  . Тогда
. Тогда 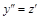 и исходное уравнение превращается в уравнение с разделяющимися переменными
и исходное уравнение превращается в уравнение с разделяющимися переменными
 .
.
Т.к.  , то последнее уравнение является дифференциальным уравнением с разделяющимися переменными
, то последнее уравнение является дифференциальным уравнением с разделяющимися переменными

 .
.
Получили общее решение исходного уравнения  . ▼
. ▼
Пример 4. Найти общее решение уравнения  .
.
▲ В уравнении нет в явном виде аргумента x. Понизим порядок уравнения подстановкой  , тогда
, тогда  и исходное уравнение превращается в уравнение с разделяющимися переменными
и исходное уравнение превращается в уравнение с разделяющимися переменными
 .
.
Т.к.  , то последнее уравнение является дифференциальным уравнением 1-го порядка с разделяющимися переменными
, то последнее уравнение является дифференциальным уравнением 1-го порядка с разделяющимися переменными
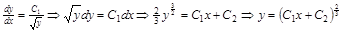 . ▼
. ▼
Пример 5. Найти общее решение уравнения  и частное решение, удовлетворяющее начальным условиям
и частное решение, удовлетворяющее начальным условиям  ,
, 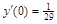 .
.
|
|
▲ Рассмотрим однородное уравнение  . Соответствующее характеристическое уравнение имеет вид
. Соответствующее характеристическое уравнение имеет вид  , откуда
, откуда  ,
,  . Следовательно,
. Следовательно,  - общее решение однородного уравнения.
- общее решение однородного уравнения.
Подберем вид частного решения для данного уравнения.

Подставляя  и
и  в неоднородное исходное уравнение, получим тождество (
в неоднородное исходное уравнение, получим тождество ( - решение данного уравнения). Для удобства вычислений будем выписывать выражения
- решение данного уравнения). Для удобства вычислений будем выписывать выражения  ,
,  ,
,  в отдельные строки и слева за вертикальной чертой помещать коэффициенты, стоящие перед ними в уравнении. Умножая эти выражения на коэффициенты, складывая и приводя подобные члены, имеем:
в отдельные строки и слева за вертикальной чертой помещать коэффициенты, стоящие перед ними в уравнении. Умножая эти выражения на коэффициенты, складывая и приводя подобные члены, имеем:

 .
.
Приравнивая коэффициенты при подобных членах в левой и правой части последнего тождества, находим  и
и  :
:

Итак, частное решение неоднородного уравнения имеет вид
 ,
,
а общее решение неоднородного уравнения -
 .
.
Найдем частное решение, удовлетворяющее заданным начальным условиям:
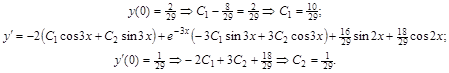
Искомое частное решение таково:
 . ▼
. ▼
Вариант контрольной работы
1. Найти общее решение дифференциальных уравнений:
а) 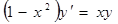 ; ;
| в) 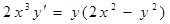 ; ;
|
б) 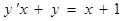 ; ;
| г) 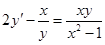 . .
|
2. Найти общее решение дифференциального уравнения
а) 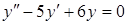 , б)
, б) 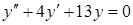 .
.
3. Определить и записать структуру частного решения 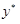 линейного неоднородного дифференциального уравнения по виду функции
линейного неоднородного дифференциального уравнения по виду функции 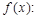
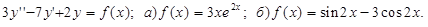
|
|
|

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!