Введение
Начальные понятия, свойства жидкости
Математики отличается от других специалистов логичностью рассуждений и строгостью доказательств.
Постараемся с учетом этого рассмотреть основы механики жидкости, проследить логику ее развития и введения понятий (гипотез)
При изучении курса будем вводить понятия и гипотезы по мере их усложнения и необходимости.
Первоначально рассмотрим жидкость, исходя из молекулярных представлений о строении материи.
1. Известно, что все тела состоят из молекул (мельчайших частиц), которые взаимодействуют между собой.
Твердые тела сохраняют свою форму из–за сильного взаимодействия (притяжения) молекул и жестких связей между ними, не позволяющих молекулам свободно перемещаться по объему, занимаемому телом.
В жидкостях силы притяжения во много раз слабее, но еще достаточны для объединения молекул в некие ансамбли (частицы).
Слабость связей между отдельными молекулами (частицами) позволяет им перескакивать с одного места на другое, что и обуславливает текучесть жидкости.
Поэтому жидкость из-за действующих на нее сил не может сохранять собственную форму, и, сохраняя лишь объем, принимать форму занимаемого ею сосуда.
Примечание:
Жидкость и твердое тело тоже меняют свой объем при изменении давления. Однако (для сравнения) при t=20° C изменение объема газа (воздуха) примерно в 14 000 раз превосходит изменение объема воды (жидкости) при равном увеличении давления.
Известны вещества, называемые газами. Слово «газ» (от греческого – хаос) было введено Ван-Гельмонотом для определения вещества, способного занимать любой, предоставленный ему объем. Эта способность объясняется крайне слабыми силами взаимного притяжения молекул, благодаря чему они могут свободно перемещаться относительно друг друга.
Внимание:
1) Таким образом жидкости отличаются от других тел свойством - текучестью.
Назовем меру легкости, с которой течет жидкость - вязкостью.
2) Поместим «газ» в резиновую оболочку. Простым сдавливанием ее убеждаемся, что на руку действует некая сила сопротивления, стремящаяся вернуть оболочке первоначальную форму.
Назовем силу сопротивления – давлением.
Численно давление равно силе сопротивления. Будем считать, что давление направлено внутрь интересующего нас объема.
Важное замечание:
Известно, что при нагревании (или охлаждении) вес тела изменяет свой объем. При этом газ во много раз больше изменяет свой объем, чем жидкость.
Вот эта особенность газа и обуславливает необходимость привлечения понятий термодинамики (теплообмена) при изучении их движения.
Теплообмен вообще говоря сказывается и на движении жидких сред. Известны, так называемые, конвективные потоки жидкости при ее нагревании, т.е. действие теплообмена в жидкости при малом изменении ее объема проявляется косвенным образом, посредством влияния температуры на механические свойства самой жидкости.
Однако в нашем курсе «чистой» гидромеханики этими явлениями (теплообмена) для жидкости будем пренебрегать, т.к. их изучением занимается теория теплообмена.
Как разделить между собой понятия газ и жидкость, учитывая, что те и другие в большей или меньшей степени обладают одинаковыми свойствами?
В связи с невозможностью такого разделения, мы будем пользоваться терминами:
«капельная жидкость» (малосжимаемая жидкость)
«сжимаемая жидкость» (газ)
«жидкость», применяя последний в широком смысле слова, охватывающем как капельную жидкость, так и газ (т.е. под жидкостью будем понимать всякую среду, обладающую свойством текучести).
Гипотеза сплошности
Исследование течения жидкости существенно упрощается, если его рассматривать не как совокупность беспорядочно движущихся частиц (молекул), а как некоторую сплошную среду, лишенную каких либо пустот и присутствующую буквально в любой точке занимаемого ею пространства.
Т.е. введем гипотезу сплошности.
Важное замечание:
Введение гипотезы сплошности позволяет нам рассматривать макроскопические параметры (например, такие, как температура, давление) непрерывно распределенными в массе текущей жидкости и, следовательно пользоваться математическим аппаратом дифференциального и интегрального исчисления.
Заметим, однако, что в действительности капельные жидкости и газы состоят из молекул, отделенных друг от друга относительно большими промежутками (особенно это относится к газам) и поэтому просто вводить удобные нам представления, вообще говоря, мы не имеем права.
Такой произвол, если он не подкреплен надежными данными, может существенным образом исказить истинные свойства среды, а, следовательно, и явления, которые в ней протекают.
Докажем правомерность использования нами сплошности:
Из курса физики известно броуновское движение. Т.е. в неподвижной среде (жидкости) наблюдается движение малых по величине объектов наблюдения. Значит, молекулярные эффекты будут проявляться и в том случае, если рассматривать движение в жидкой или газообразной среде малых по величине тел или если изучать течение этой среды в узких каналах.
Когда мы говорим «малый» или «большой», то всегда имеем в виду по сравнению с чем.
Сами по себе эти понятия бессмысленны.
Таким образом, размеры тел или каналов необходимо сравнивать с расстоянием между молекулами. А т.к. молекулы непрерывно перемещаются, то за эталон длины, очевидно, следует принять среднюю длину свободного «пробега» (пролета). Таким образом дело не только в том, сколько молекул содержится в малых объемах (хотя в мм3 воздуха при норм. условиях содержится 2,7 ∙1016 молекул), а в том, каково соотношение между характерным размером канала (для труб это Ø) или омываемого тела по сравнению со средней длиной свободного «пробега».
Важное замечание:
Принято считать, что если соотношение между характерными размерам канала и длиной свободного пробега молекулы составляет величину порядка 105 и выше, то молекулярные эффекты уже не могут себе проявить и исследуемое течение можно рассматривать как течение сплошной среды.
Договоримся, что мы рассматриваем только случаи течения, в которых это условие всегда выполняется.
Объемные (массовые) силы
Объемными (массовыми) силами назовем силы, которые действуют на все частицы жидкости внутри любого выделенного объема.
Такими силами являются гравитационные (сила тяжести) и инерционная (сила инерции, возникающая при изменении скорости движения жидкости).
Роль этих сил неодинакова. Так:
1. Сила тяжести оказывает слабое влияние на процесс течения и ею будем пренебрегать.
2. Пренебрежение силами инерции недопустимо. Т.к. исключение их из уравнений движения жидкости существенно искажает истинную картину течения.
Примечание: инерционные силы не проявляют себя лишь тогда, когда жидкость движется без ускорения.
Поверхностные силы
Поскольку нами принята гипотеза сплошности, то, выделяя некоторый объем ΔV, мы можем говорить о поверхности, отделяющей этот объем от остальной массы жидкости.
По этой поверхности будут распределены каким-то образом силы взаимодействия выделенного объема с окружающими его частями среды или твердыми стенками.
Таким образом, мы вводим понятие поверхностных сил.
Возьмем достаточно малых элемент ΔS этой поверхности, чтобы его можно было считать плоским.
Разложим силу Δ  , действующую на выделенный элемент, на две составляющие: нормальную и касательную.
, действующую на выделенный элемент, на две составляющие: нормальную и касательную.
Рассмотрим их по отдельности.
Касательные силы
Ранее мы отметили, что жидкость отличается от твердых тел - текучестью. Т.е. если к жидкости приложены силы, то она ни на мгновение не способна их сдерживать и начинает течь. Мера легкости, с которой течет жидкость определяется ее вязкостью.
Введем математическое определение этого важнейшего свойства жидкости.
Вначале введем понятие напряжения касательных сил в точке. Для этого перейдем к пределу в отношении 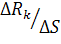 при ΔS → 0 и получим значение напряжения касательной силы в некоторой точке, принадлежащей элементарной площадке ΔS:
при ΔS → 0 и получим значение напряжения касательной силы в некоторой точке, принадлежащей элементарной площадке ΔS:
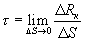 (2.8)
(2.8)
Ранее мы отмечали, что касательные напряжения в неподвижной жидкости отсутствуют. Они возникают только при проскальзывании одних частиц среды относительно других, т.е. зависят от относительной скорости скольжения жидкости по поверхности ΔS. Очевидно, что чем больше эта скорость, тем больше касательные усилия и тем заметнее проявляется вязкость жидкости.
Казалось бы в рассматриваемой точке не может быть разности скорости (т.е. скорости скольжения) из-за введения нами гипотезы сплошности и следующей из нее непрерывности изменения скорости жидкости. Однако в различных точках движущейся жидкости скорость различна. Значит, можно говорить об изменении скорости в данной точке, т.е. о производной от скорости, которая и определяет скорость относительного смещения одних точек жидкости относительно других. Поскольку нас интересует взаимное скольжение частиц жидкости вдоль поверхности ΔS, то логично взять производную от касательной составляющей скорости к этой поверхности по нормали к ней. Эта величина и будет определять скорость взаимного скольжения в интересующей нас точке.
Но в какой мере касательные напряжения зависят от производной 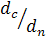 (здесь с – касательная сост. скор. к рассматр. пов. ΔS)
(здесь с – касательная сост. скор. к рассматр. пов. ΔS)
Ньютон в 1687 году предложил гипотезу, между величинами  и
и 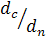 существует прямопропорциональная зависимость. Т.е. касательные напряжения (напряжение трения) могут вычисляться в движущихся средах по формуле
существует прямопропорциональная зависимость. Т.е. касательные напряжения (напряжение трения) могут вычисляться в движущихся средах по формуле
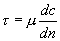 (2.9)
(2.9)
где 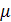 - коэффициент пропорциональности, называемый коэффициентом динамической вязкости.
- коэффициент пропорциональности, называемый коэффициентом динамической вязкости.
Т.о., в соответствии с предположением Ньютона, динамическая вязкость 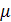 определяется исключительно физическими свойствами среды (т.е. эти свойства, в том числе и
определяется исключительно физическими свойствами среды (т.е. эти свойства, в том числе и 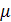 , могут зависеть от температуры и давления, но не зависят от распределения скоростей в потоке жидкости).
, могут зависеть от температуры и давления, но не зависят от распределения скоростей в потоке жидкости).
Замечание:
Эта Гипотеза Ньютона является всего лишь предположением, истинность или ложность которого может быть проверена опытом или теоретическими методами других наук.
Проверка гипотезы Ньютона показала, что она справедлива для большинства жидкостей и поэтому уравнение (2.9) трактуется как математическое выражение закона трения, а величину 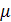 рассматривают как физическую константу, зависящую от свойств среды.
рассматривают как физическую константу, зависящую от свойств среды.
Жидкости, которые подчиняются закону трения Ньютона, называются ньютоновскими.
Однако существует множество жидкостей (расплавы полимеров, коллоидные растворы, суспензии и т.д.), которые закону трения Ньютона не удовлетворяют.
Жидкости, которые не подчиняются закону трения Ньютона, называются неньютоновскими.
Мы в нашем курсе будем рассматривать лишь ньютоновские жидкости.
Для облегчения и удобства решения задач гидромеханики введем модель (понятия) идеальной жидкости.
Под идеальной жидкостью будем понимать воображаемую жидкость, обладающую абсолютной подвижность (т.е. лишенную вязкости), абсолютно несжимаемую, не расширяющуюся с изменением температуры, абсолютно не способную сопротивляться разрыву (растягивающим усилиям).
Оказывается там, где силы вязкости вносят небольшие поправки к основному движению, где нужно выявить главные особенности течения, модель идеальной жидкости чрезвычайно удобна.
Замечание:
Понятие идеальной жидкости не следует смешивать с понятием идеального газа, которое установилось в термодинамике.
В курсе механики жидкости идеальным газом по-прежнему (аналогично термодинамике) называется газ, подчиняющийся уравнению состояния Клапейрона.
Нормальные силы
Давление
Естественно, что изучение поведения жидкости под действием различных сил наиболее целесообразно начать с условий ее равновесия.
Говоря о равновесии жидкости, будем подразумевать под этим термином состояние покоя одних ее частиц относительно других внутри рассматриваемого объема ΔV конечных размеров.
Т.о. мы не ограничиваем себя рассмотрением лишь неподвижной жидкости (т.к., как известно, движение и покой есть понятия относительные). Т.е. жидкость может перемещаться, ставится лишь условие, чтобы вся интересующая нас масса жидкости, заключенная в выделенном объеме ΔV, двигалась как единое целое.
Рассмотрим условия, которым должны удовлетворять поверхностные силы при равновесии жидкости.
Повторим рассуждения, сделанные в начале раздела 2.3.2. (поверхностные силы).
Т.е. выделим некоторый объем ΔV жидкости, находящейся в равновесии. На поверхности, отделяющей этот объем от остальной массы жидкости, возьмем такой достаточно малый элемент ΔS, чтобы его можно было считать плоским.
Пусть равнодействующая всех сил Δ  , действующая на этот элемент, приложена в некоторой точке M
, действующая на этот элемент, приложена в некоторой точке M 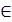 ΔS.
ΔS.
Разлагая эту силу по нормали и касательной к элементу ΔS, мы получаем 2 силы: нормальную ΔRH и касательную ΔRK.
Нормальная сила ΔRH вжимает (вдавливает) элемент ΔS в объем ΔV, и, поскольку жидкость сопротивляется сжатию, возникает сила противодействия, которая уравновешивает силу ΔRH и обеспечивает равновесие жидкости.
Касательная сила ΔRK стремиться сдвинуть элемент ΔS. Чтобы сдвига не произошло и равновесие не нарушилось необходимо соблюдение условия, чтобы ΔRK=0.
Т.о. для равновесия элемента ΔS необходимо, чтобы действующая на него сила была сжимающей (т.е. направлена по внутренней нормали к граничной поверхности).
Вывод:
1. Для сохранения равновесия массы жидкости необходимо, чтобы внешние силы, действующие в точках ее граничной поверхности, были направлены только по внутренним нормалям к этой поверхности.
2. Все частицы внутри жидкости, находящейся в равновесии, испытывают всестороннее сжатие.
Отношение  (2.10), очевидно, представляет собой «напряжение», т.е. силу, приходящуюся на единицу площади.
(2.10), очевидно, представляет собой «напряжение», т.е. силу, приходящуюся на единицу площади.
Т.к. при равновесии жидкости ΔRH является сжимающей силой, то 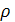 представляет собой среднее для данного элемента поверхности напряжение сжатия, которое называют средним гидростатистическим давлением на элементе ΔS.
представляет собой среднее для данного элемента поверхности напряжение сжатия, которое называют средним гидростатистическим давлением на элементе ΔS.
Для определения точного значения давления в данной точке переходят к пределу в отношении 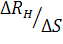 при ΔS → 0, т.е.
при ΔS → 0, т.е.
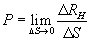 (2.11)
(2.11)
Замечание:
1. Если в жидкости, находящейся в равновесии, выделить элементарную площадку ΔS, проходящую через некоторую точку M, то при любой ориентации площадки относительно точки M сила давления на нее будет оставаться неизменной.
Примечание:
Это утверждение называется законом Паскаля или основной теоремой гидростатики.
2. Силы давления проявляют себя и в движущейся среде. Там они части взаимосвязаны со скоростью течения. Но это не означает, что изменение скорости является причиной появления или изменения давления. Взаимосвязь давления и скорости при движении жидкости объясняются тем, что под влиянием внешних воздействий в потоке энергия перераспределяется между ее различными формами, что в конечном итоге сказывается на величине давления и скорости.
Тензоры
В нашем курсе гидромеханики с тензорными величинами много работать не придется, поэтому ограничимся лишь самими необходимыми сведениями.
Рассмотрим операцию деления векторов. Пусть 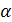 есть частное от деления векторов
есть частное от деления векторов  и
и 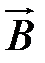 :
:
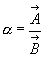 (3.1)
(3.1)
Пока не интересуяся тем, как выполняется деление, поставим перед собой вопрос: какого класса есть величина 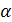 ? (т.е. что это – скаляр, вектор или нечто новое?)
? (т.е. что это – скаляр, вектор или нечто новое?)
Перепишем (3.1) так:
 (3.2)
(3.2)
Допустим, что 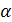 - это скаляр. Тогда векторы
- это скаляр. Тогда векторы  и
и 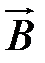 отличаются только модулем, направление же их либо одинаково, либо противоположено, т.е. эти векторы коллинеарны.
отличаются только модулем, направление же их либо одинаково, либо противоположено, т.е. эти векторы коллинеарны.
Таким образом очевидно, что 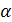 скаляром быть не может, так как этой величиной мы определили частное от деления двух любых векторов, а не только коллинеарных.
скаляром быть не может, так как этой величиной мы определили частное от деления двух любых векторов, а не только коллинеарных.
Рассуждая подобным образом, легко установим, что 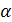 не может принадлежать и к классу векторов, поскольку тогда под
не может принадлежать и к классу векторов, поскольку тогда под  следует понимать векторное произведение и, значит векторы
следует понимать векторное произведение и, значит векторы  и
и 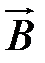 должны быть взаимно перпендикулярны.
должны быть взаимно перпендикулярны.
Таким образом ни скаляр, ни вектор не могут в общем случае представлять результат частного деления двух произвольно выбранных векторов.
Остается заключить,что 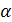 есть величина иного ранга, которая называется тензором.
есть величина иного ранга, которая называется тензором.
Из равенства (3.2) следует, что вектор 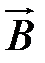 будучи умножен на тензор
будучи умножен на тензор 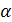 , дает новый вектор
, дает новый вектор  .
.
Таким образом равенство (3.2) можно рассматривать как определение тензора, т.е. под тензором будем понимать новую величину, которая преобразует один вектор в другой.
Преобразование одного вектора в другой (в нашем примере 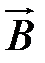 в
в  ) можно осуществлять различными способами. Можно, к примеру, взять составляющие исходного вектора
) можно осуществлять различными способами. Можно, к примеру, взять составляющие исходного вектора 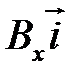 ,
, 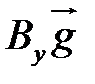 ,
, 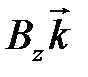 и просто изменить длину каждого из них, что эквивалентно умножению скалярных величин Вх, Вy, Вz на некоторые числа
и просто изменить длину каждого из них, что эквивалентно умножению скалярных величин Вх, Вy, Вz на некоторые числа 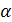 xx,
xx, 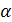 yy,
yy, 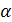 zz.
zz.
В результате получим:
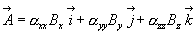 (3.3)
(3.3)
Но это далеко не самый общий вид преобразования, а один из наиболее простых.
Вообще, говоря о преобразовании векторов, целесообразнее было бы ввести более широкое представление о такой операции.
Очевидно, что если вместе с изменением длины каждого из векторов 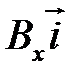 ,
, 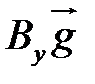 ,
, 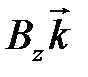 будет осуществлен их поворот на некоторые углы в пространстве, то сумма этих новых векторов дает вместо исходного вектора
будет осуществлен их поворот на некоторые углы в пространстве, то сумма этих новых векторов дает вместо исходного вектора 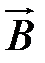 другой вектор
другой вектор  .
.
Формально результат такого преобразования будет состоять в замене векторов  ,
,  ,
, 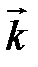 векторами
векторами  ,
, 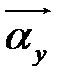 ,
,  такими, что
такими, что
 (3.4)
(3.4)
Сопоставляя равенства (3.4) и (3.2), можно утверждать, что векторы  ,
, 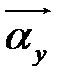 ,
,  образуют тензор
образуют тензор 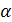 .
.
Замечание:
Тензор 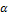 не есть сумма векторов
не есть сумма векторов  ,
, 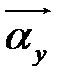 ,
,  , а совокупность этих векторов составляет тензор. Это аналогично тому, что совокупность скалярных величин Вх, Вy, Вz составляют вектор
, а совокупность этих векторов составляет тензор. Это аналогично тому, что совокупность скалярных величин Вх, Вy, Вz составляют вектор 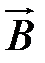 .
.
Условно это можно записать так:
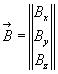 (3.5)
(3.5)
Двойная черта, ограничивающая матрицу, ставится для того, чтобы отличить ее от определителя, в котором предполагаются некоторые действия над его элементами, в то время как в матрице эти действия не подразумеваются.
 (3.6)
(3.6)
Зная, что векторы  ,
, 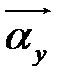 ,
,  , имеют проекции на оси координат, равные αxx, αxy, αxz, αyx, αyy, αyz и т.д., тензор можно представить таблицей (матрицей) из девяти скалярных величин:
, имеют проекции на оси координат, равные αxx, αxy, αxz, αyx, αyy, αyz и т.д., тензор можно представить таблицей (матрицей) из девяти скалярных величин:
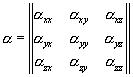 (3.7)
(3.7)
В записи (3.7) тензора α первый индекс означает строку, а второй столбец, встречается такая запись:
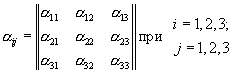 (3.8)
(3.8)
Такой тензор называют тензором второго ранга (по числу индексов у компонент).
Тензор – более общее понятие, чем вектор или скаляр. Компоненты вектора имеют один индекс (смотри запись (3.5)) или 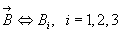 т.е. вектор может быть записан матрицей (таблицей) из одного столбца.
т.е. вектор может быть записан матрицей (таблицей) из одного столбца.
Вектор называют тензором первого ранга.
Скаляр, представляемый буквой без индекса (a = a(x,y,z)), называют тензором нулевого ранга.
Тензор второго ранга (3.7) в общем случае записывается девятью функциями трех переменных.
Замечание:
Вектор  может быть получен из вектора
может быть получен из вектора 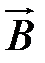 с помощью неединственной тройки векторов
с помощью неединственной тройки векторов  ,
, 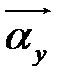 ,
,  .
.
Существует бесчисленное множество комбинаций векторов  ,
, 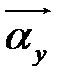 ,
,  (т.е. бесчисленное количество тензоров α), которые преобразуют вектор
(т.е. бесчисленное количество тензоров α), которые преобразуют вектор 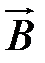 в один и тот же вектор
в один и тот же вектор  . Это значит, что операция деления векторов многозадачна, она не дает единственного результата (именно по этому и не употребляется в векторном исчислении).
. Это значит, что операция деления векторов многозадачна, она не дает единственного результата (именно по этому и не употребляется в векторном исчислении).
Однако если тензор α уже определен, то умножение его на вектор приводит к единственному решению и использование такой операции вполне целесообразно.
Grad Р (градиент давления)
Пусть под скаляром мы будем понимать давление P.
Рассмотрим подынтегральное выражение входящее в формулу (3.18)
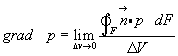
Под знаком интеграла содержится произведение p∙dF, которое дает величину силы давления, приложенного к площадке dF.
После умножения не единичный нормальный вектор  получаем направление действия этой силы, поскольку давление всегда действует по нормали к рассматриваемой площадке.
получаем направление действия этой силы, поскольку давление всегда действует по нормали к рассматриваемой площадке.
Выделим в пространстве некоторый объем ΔV или будем рассматривать одну и ту же массу жидкости, занимающую объем ΔV, (в данном случае различие точек зрения не меняет смысла понятия градиента давления), тогда величина -  pdF дает величину и направление силы давления на этот объем по площадке dF.
pdF дает величину и направление силы давления на этот объем по площадке dF.
Знак минус поставлен на том основании, что давление действует всегда по внутренней нормали, а в формуле рассматривается внешняя нормаль  к поверхности, охватывающей объем ΔV.
к поверхности, охватывающей объем ΔV.
Проинтегрируем теперь по замкнутой поверхности F и получим суммарную силу давления на объем ΔV:
 (3.21)
(3.21)
Разделив равенство (3.21) на величину объема ΔV, получим среднее значение силы давления, действующей на единичный объем, заключенный внутри поверхности F.
При ΔV → 0 предел этого отношения дает точное значение величины и направления суммарной силы давления, которой подвергается единичный объем, охватывающий интересующую нас точку пространства или центр инерции движущейся бесконечно малой частички жидкости.
3.2.3 rot 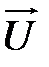 (ротор скорости)
(ротор скорости)
Анализируя выражение (3.19), т.е.

и рассматривая частицу жидкости произвольной формы, как это делали при обсуждении div 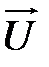 и grad P, невозможно дать физическое трактование rot
и grad P, невозможно дать физическое трактование rot 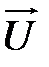 .
.
Замечание: rot 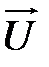 представляет собой удвоенную угловую скорость вращения частицы жидкости в рассматриваемой точке пространства, т.е.
представляет собой удвоенную угловую скорость вращения частицы жидкости в рассматриваемой точке пространства, т.е.
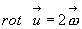 (3.22)
(3.22)
Символическое исчисление
Оператор Гамильтона
Рассмотрев внимательно математическое содержание операций div, grad, rot (формулы 3.17, 3.18, 3.19), замечаем, что эти три соотношения могут быть представлены одним общим выражением вида:
 (*)
(*)
где символ 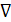 …, называемый оператором Гамильтона или вектором Набла, обозначает предел отношения, стоящий в правой части равенств 3.17, 3.18, 3.19.
…, называемый оператором Гамильтона или вектором Набла, обозначает предел отношения, стоящий в правой части равенств 3.17, 3.18, 3.19.
Известна запись определения производной от функции
 (**)
(**)
Запись (*) и (**) имеют сходство и различие.
1. Сходство записей (*) и (**):
В записи (**) под знаком предела стоит разность значений (изменения) функции на границах интервала Δx, отнесенная к величине самого интервала.
В записи (*) также под знаком предела стоит отношение изменения (разности) значений некоторой величины (представляемое интегралом по поверхности) на границах интервала к самому интервалу ΔV.
Однако в выражении (**) рассматривается линейный интервал, в в выражении (*) трехмерный.
Поэтому знак 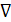 можно трактовать, подобно символу
можно трактовать, подобно символу 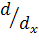 , как оператор дифференцирования, но не по одной координате, а по всем трем координатам сразу, т.е. по объему.
, как оператор дифференцирования, но не по одной координате, а по всем трем координатам сразу, т.е. по объему.
2. Различие записей (*) и (**)
Известно, что оператор 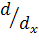 , примененный к скалярной функции, всегда дает скалярную величину, а к векторной – векторную. Но мы ранее установили, что дивергенция вектора – скаляр, градиент скаляра – вектор, ротор вектора – вектор.
, примененный к скалярной функции, всегда дает скалярную величину, а к векторной – векторную. Но мы ранее установили, что дивергенция вектора – скаляр, градиент скаляра – вектор, ротор вектора – вектор.
Т.е., казалось бы, применение оператора дифференцирования 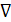 к векторным и скалярным функциям не приводит к однозначности результатов. Однако будем считать, что знак
к векторным и скалярным функциям не приводит к однозначности результатов. Однако будем считать, что знак  имеет двойственную природу, являясь одновременно и оператором дифференцирования, и особым символическим вектором, т.е. вектором, не имеющим не определенной длины, ни направления.
имеет двойственную природу, являясь одновременно и оператором дифференцирования, и особым символическим вектором, т.е. вектором, не имеющим не определенной длины, ни направления.
Замечание:
Исходя из двойственности (двойственной природы) символа 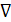 , строится изящное исчисление, широко применяемое в векторном анализе.
, строится изящное исчисление, широко применяемое в векторном анализе.
т.о.
 (3.23)
(3.23)
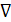 ∙
∙ 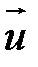 - есть скалярное произведение вектора набла на вектор скорости (и в то же время определенным образом выполненное дифференцирование), поэтому ясно, что дивергенция вектора есть скорость.
- есть скалярное произведение вектора набла на вектор скорости (и в то же время определенным образом выполненное дифференцирование), поэтому ясно, что дивергенция вектора есть скорость.
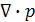 - есть вектор (умножение вектора на скаляр), но в то же время осуществляется дифференцирование скалярной функции по объему.
- есть вектор (умножение вектора на скаляр), но в то же время осуществляется дифференцирование скалярной функции по объему.
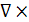
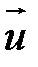 - есть векторное произведение вектора набла на вектор скорости, что дает производный вектор получившийся в результате определенным образом проведенного дифференцирования векторной функции по объему.
- есть векторное произведение вектора набла на вектор скорости, что дает производный вектор получившийся в результате определенным образом проведенного дифференцирования векторной функции по объему.
Замечание:
В векторном анализе в основном действуют все те правила, которые справедливы для дифференциального исчисления обычных скалярных функций, однако имеется и некоторое отличие.
Дифференциальные тензоры
Составим диадное произведение вектора набла 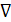 и какого-нибудь переменного вектора, например
и какого-нибудь переменного вектора, например 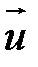 .
.
Помня, что умножить на составляющую символического вектора 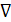 - это значит продифференцировать по соответствующей координате, находим:
- это значит продифференцировать по соответствующей координате, находим:
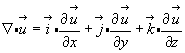 (3.44)
(3.44)
Этот тензор по аналогии с градиентом скалярной величины (см. формулу 3.33) назовем градиентом вектора:
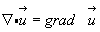 (3.42)
(3.42)
Его составляющие легко выявляются, если рассмотреть диадные произведения ортов на скалярные производные от вектора 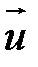 в равенстве (3.41), и записываются в виде матрицы:
в равенстве (3.41), и записываются в виде матрицы:
Примечание:
Свойство сопряженного тензора:
Величина произведения вектора на тензор, не изменится, если при перестановке сомножителей тензор заменить на сопряженный.
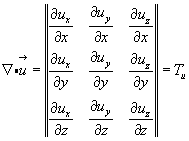 (3.43)
(3.43)
Умножим тензор grad 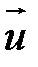 на дифференциал радиус вектора слева:
на дифференциал радиус вектора слева:
 (3.44)
(3.44)
Полученное соотношение совершенно аналогично (3.37) полному дифференциалу скалярной функции. Т.е. имеем:
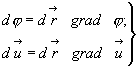 (3.44а)
(3.44а)
Если в тензоре (3.43) заменить элементы строк на элементы столбцов, то получим сопряженный тензор:
 (3.45)
(3.45)
Если в другой записи (с учетом (3.6) и (3.7)):
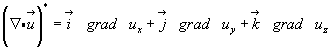 (3.46)
(3.46)
но по свойству сопряженного тензора равенство (3.44а) можно переписать в следующем виде:
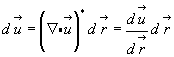 (3.47)
(3.47)
Следовательно, тензор (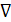 ∙
∙ 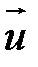 )* можно рассматривать как производную от векторной функции
)* можно рассматривать как производную от векторной функции 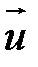 по векторному аргументу
по векторному аргументу 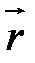 .
.
Виды движения жидкости
Представим себе, что мы последовательно фотографируем поток жидкости в некоторой области в различные моменты времени.
Если после проявления фотографий будет обнаружено, что они ничем не отличаются одна от другой, то имеем установившееся движение. Т.о. в установившемся времени в каждой точке пространства все параметры (такие как давление, скорость, температура, плотность и др.) движущейся жидкости остаются неизменными.
Если фотографии будут отличаться друг от друга, то имеем неустановившееся движение. При таком движении все параметры жидкости меняются не только от одной точки пространства к другой, но и в каждой точке с течением времени.
Замечание:
Установившееся движение – это предельный случай неустановившегося. Т.е. такое движение к которому придет неустановившееся движение если прекратить изменение внешних воздействий.
Ускорение жидкой частицы
Рассмотрим в качестве параметра скорость жидкой частицы 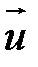 .
.
Воспользуемся формулой (4.17) и в результате получим векторную форму записи ускорения жидкой частицы.
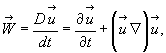 (4.18)
(4.18)
где 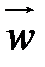 - называется субстанциональным (полным) ускорением;
- называется субстанциональным (полным) ускорением;
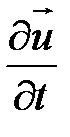 - локальным ускорением;
- локальным ускорением;
(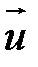
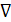 )
) 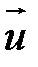 - конвекторным ускорением.
- конвекторным ускорением.
Замечание:
1. Локальное ускорение определяется изменением вектора скорости в данной точке пространства.
2. Конвективное ускорение возникает вследствие того, что частица жидкости в процессе движения перемещается из данной точки в другую, в которой вектор скорости отличается от первоначального.
Из этого следует, что:
1. Если поле вектора однородно (т.е. вся жидкость перемещается поступательно как твердое тело), то конвективное ускорение равно нулю и все ускорение сводится к локальному, одинаковому во всех точках пространства, занятого движущейся жидкостью.
2. Если движение жидкости является установившимся (т.е. скорость жидкости в каждой точке не меняется с течением времени), то локальное ускорение отсутствует, а имеется лишь конвективное.
Перейдем от векторной формы записи ускорения к координатной. В результате с учетом (3.36) получим:
 (4.19)
(4.19)
Встречается и другая векторная запись ускорения. Перепишем (4.19), заменив порядок сомножителей.
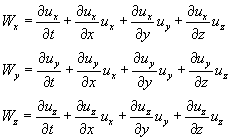
Используя формулы произведения тензора на вектор (3.4) и (3.7) и выражение дифференциального тензора векторного поля (3.42) и (3.45), можно представить вектор ускорения в следующей компактной форме:
 (4.20)
(4.20)
где

Для исследования (изучения) вихревого движения выражение (4.20) для ускорения следует преобразовать, вводя компоненты вихря.
В соответствии с равенством (3.11) разложим тензор Tu* на симметричную и антисимметричную часть
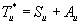 (4.21)
(4.21)
причем, как это следует из (4.8)
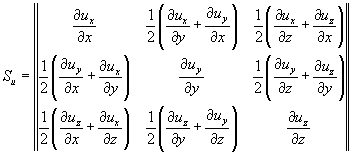
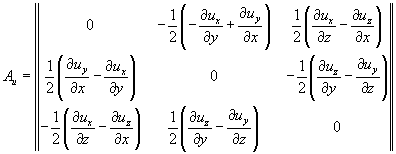
из выражения (3.34) следует, что:
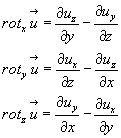
Поэтому тензор Аu можем переписать в следующем виде:
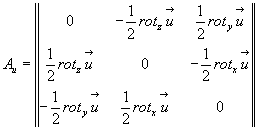 (4.22)
(4.22)
Умножим дифференциальный тензор Tu* поля вектора 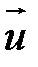 на произвольный вектор
на произвольный вектор 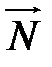 с проекциями Nx, Ny, Nz. Очевидно, что
с проекциями Nx, Ny, Nz. Очевидно, что
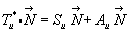 (4.23)
(4.23)
Представим произведение Аu 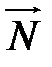 в развернутом виде. В соответствии с (3.3) и (4.22) можем записать:
в развернутом виде. В соответствии с (3.3) и (4.22) можем записать:
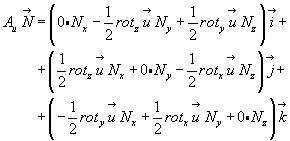 (4.24)
(4.24)
Этот же вектор Аu 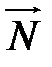 представим в другой форме. Для этого запишем (определим) векторное произведение rot
представим в другой форме. Для этого запишем (определим) векторное произведение rot 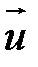 на
на 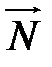
 (4.25)
(4.25)
Сравнивая выражения (4



 , действующую на выделенный элемент, на две составляющие: нормальную и касательную.
, действующую на выделенный элемент, на две составляющие: нормальную и касательную.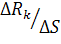 при ΔS → 0 и получим значение напряжения касательной силы в некоторой точке, принадлежащей элементарной площадке ΔS:
при ΔS → 0 и получим значение напряжения касательной силы в некоторой точке, принадлежащей элементарной площадке ΔS: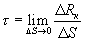 (2.8)
(2.8)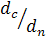 (здесь с – касательная сост. скор. к рассматр. пов. ΔS)
(здесь с – касательная сост. скор. к рассматр. пов. ΔS) и
и 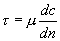 (2.9)
(2.9)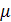 - коэффициент пропорциональности, называемый коэффициентом динамической вязкости.
- коэффициент пропорциональности, называемый коэффициентом динамической вязкости.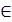 ΔS.
ΔS. (2.10), очевидно, представляет собой «напряжение», т.е. силу, приходящуюся на единицу площади.
(2.10), очевидно, представляет собой «напряжение», т.е. силу, приходящуюся на единицу площади.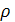 представляет собой среднее для данного элемента поверхности напряжение сжатия, которое называют средним гидростатистическим давлением на элементе ΔS.
представляет собой среднее для данного элемента поверхности напряжение сжатия, которое называют средним гидростатистическим давлением на элементе ΔS.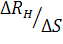 при ΔS → 0, т.е.
при ΔS → 0, т.е.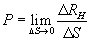 (2.11)
(2.11)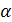 есть частное от деления векторов
есть частное от деления векторов  и
и 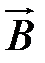 :
: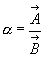 (3.1)
(3.1) (3.2)
(3.2) следует понимать векторное произведение и, значит векторы
следует понимать векторное произведение и, значит векторы 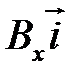 ,
, 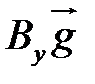 ,
, 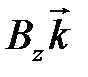 и просто изменить длину каждого из них, что эквивалентно умножению скалярных величин Вх, Вy, Вz на некоторые числа
и просто изменить длину каждого из них, что эквивалентно умножению скалярных величин Вх, Вy, Вz на некоторые числа 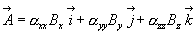 (3.3)
(3.3) ,
,  ,
, 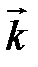 векторами
векторами  ,
, 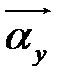 ,
,  такими, что
такими, что (3.4)
(3.4)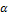 не есть сумма векторов
не есть сумма векторов 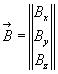 (3.5)
(3.5) (3.6)
(3.6)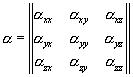 (3.7)
(3.7)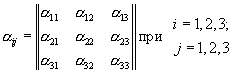 (3.8)
(3.8)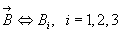 т.е. вектор может быть записан матрицей (таблицей) из одного столбца.
т.е. вектор может быть записан матрицей (таблицей) из одного столбца.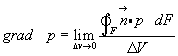
 получаем направление действия этой силы, поскольку давление всегда действует по нормали к рассматриваемой площадке.
получаем направление действия этой силы, поскольку давление всегда действует по нормали к рассматриваемой площадке. (3.21)
(3.21)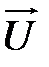 (ротор скорости)
(ротор скорости)
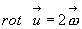 (3.22)
(3.22) (*)
(*)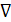 …, называемый оператором Гамильтона или вектором Набла, обозначает предел отношения, стоящий в правой части равенств 3.17, 3.18, 3.19.
…, называемый оператором Гамильтона или вектором Набла, обозначает предел отношения, стоящий в правой части равенств 3.17, 3.18, 3.19. (**)
(**)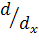 , как оператор дифференцирования, но не по одной координате, а по всем трем координатам сразу, т.е. по объему.
, как оператор дифференцирования, но не по одной координате, а по всем трем координатам сразу, т.е. по объему. имеет двойственную природу, являясь одновременно и оператором дифференцирования, и особым символическим вектором, т.е. вектором, не имеющим не определенной длины, ни направления.
имеет двойственную природу, являясь одновременно и оператором дифференцирования, и особым символическим вектором, т.е. вектором, не имеющим не определенной длины, ни направления. (3.23)
(3.23)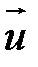 - есть скалярное произведение вектора набла на вектор скорости (и в то же время определенным образом выполненное дифференцирование), поэтому ясно, что дивергенция вектора есть скорость.
- есть скалярное произведение вектора набла на вектор скорости (и в то же время определенным образом выполненное дифференцирование), поэтому ясно, что дивергенция вектора есть скорость.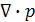 - есть вектор (умножение вектора на скаляр), но в то же время осуществляется дифференцирование скалярной функции по объему.
- есть вектор (умножение вектора на скаляр), но в то же время осуществляется дифференцирование скалярной функции по объему.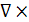
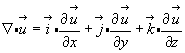 (3.44)
(3.44)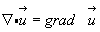 (3.42)
(3.42)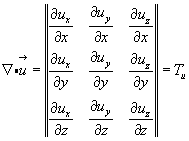 (3.43)
(3.43) (3.44)
(3.44)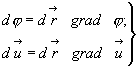 (3.44а)
(3.44а) (3.45)
(3.45)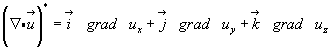 (3.46)
(3.46)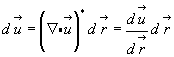 (3.47)
(3.47)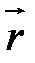 .
.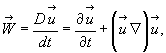 (4.18)
(4.18)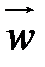 - называется субстанциональным (полным) ускорением;
- называется субстанциональным (полным) ускорением;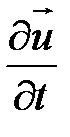 - локальным ускорением;
- локальным ускорением; (4.19)
(4.19)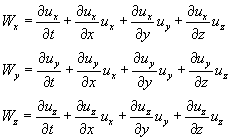
 (4.20)
(4.20)
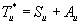 (4.21)
(4.21)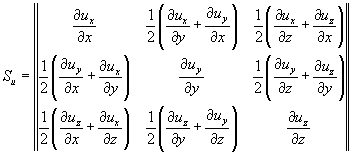
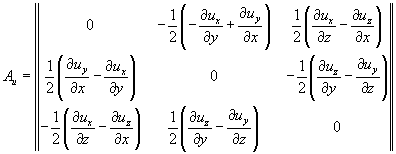
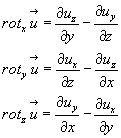
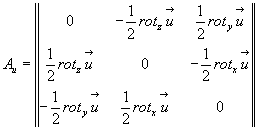 (4.22)
(4.22)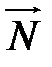 с проекциями Nx, Ny, Nz. Очевидно, что
с проекциями Nx, Ny, Nz. Очевидно, что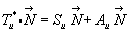 (4.23)
(4.23)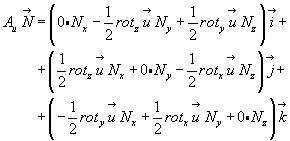 (4.24)
(4.24) (4.25)
(4.25)


