Определение. Линейным дифференциальным уравнением первого порядка называется уравнение вида
 (1.28)
(1.28)
где  – непрерывные на некотором интервале
– непрерывные на некотором интервале 
 функции.
функции.
По теореме существования и единственности решения задачи Коши (см. п.1.1) через каждую точку полосы

проходит одна и только одна интегральная кривая рассматриваемого уравнения.
Если  то уравнение (1.28) называется однородным линейным дифференциальным уравнением.
то уравнение (1.28) называется однородным линейным дифференциальным уравнением.
Это уравнение с разделяющимися переменными, его общее решение есть
 (1.29)
(1.29)
где  произвольная постоянная, а
произвольная постоянная, а  означает первообразную функцию для функции
означает первообразную функцию для функции  .
.
При  уравнение (1.28) называется неоднородным. При интегрировании неоднородного линейного дифференциального уравнения (1.28) применяют так называемый метод вариации произвольной постоянной или метод Лагранжа. Этот метод состоит в том, что общее решение ОДУ (1.28) ищут в таком же виде, что и общее решение соответствующего ему однородного уравнения, т.е. в виде (1.29). Но при этом считают произвольную постоянную
уравнение (1.28) называется неоднородным. При интегрировании неоднородного линейного дифференциального уравнения (1.28) применяют так называемый метод вариации произвольной постоянной или метод Лагранжа. Этот метод состоит в том, что общее решение ОДУ (1.28) ищут в таком же виде, что и общее решение соответствующего ему однородного уравнения, т.е. в виде (1.29). Но при этом считают произвольную постоянную  непрерывно дифференцируемой функцией от
непрерывно дифференцируемой функцией от 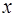 . Иллюстрацию метода проведем на следующих примерах.
. Иллюстрацию метода проведем на следующих примерах.
Пример 1. Проинтегрировать дифференциальное уравнение
 . (1.30)
. (1.30)
Решение. Перепишем данное уравнение в виде
 (1.31)
(1.31)
Уравнение (1.31) - неоднородное линейное дифференциальное уравнение. Однородное уравнение, соответствующее (1.31), есть уравнение вида

которое имеет общее решение

или
 (1.32)
(1.32)
Общее решение ОДУ (1.31) будем искать в виде (1.32), где  считаем непрерывно дифференцируемой функцией от
считаем непрерывно дифференцируемой функцией от  , т.е. в виде
, т.е. в виде
 . (1.33)
. (1.33)
Из (1.33) находим
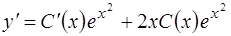 .
.
Подставляя  из (1.33) и найденное выражение
из (1.33) и найденное выражение 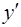 в уравнение (1.31), получаем следующее дифференциальное уравнение для определения
в уравнение (1.31), получаем следующее дифференциальное уравнение для определения  :
:

или
 .
.
Из последнего находим 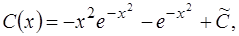 где
где  произвольная постоянная. Подставив
произвольная постоянная. Подставив  в (1.33), получим общее решение ОДУ (1.31):
в (1.33), получим общее решение ОДУ (1.31):
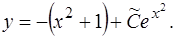
Оно, очевидно, есть общее решение и уравнения (1.30).
Пример 2. Найти интегральную кривую уравнения
 (1.34)
(1.34)
проходящую через точку  .
.
Решение. Считая  функцией от
функцией от  , приведем данное уравнение к линейному относительно
, приведем данное уравнение к линейному относительно  . Для этого обе части (1.34) умножим на функцию
. Для этого обе части (1.34) умножим на функцию 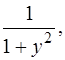 тогда будем иметь
тогда будем иметь
 . (1.35)
. (1.35)
Уравнение (1.35) проинтегрируем методом Лагранжа. Общее решение однородного линейного уравнения, соответствующего (1.35), есть

или

Последнее соотношение перепишем в виде
 . (1.36)
. (1.36)
Общее решение ОДУ (1.35) также будем искать в виде (1.36), при этом считаем  С учетом последнего из (1.36) находим
С учетом последнего из (1.36) находим 
 .
.
Подставим  и
и  в (1.35), получим дифференциальное уравнение для определения
в (1.35), получим дифференциальное уравнение для определения  :
:

или

Из последнего уравнения находим
 ,
,
где  произвольная постоянная. Подставим
произвольная постоянная. Подставим  вместо
вместо 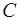 в (1.36), найдем общее решение уравнения (1.35)
в (1.36), найдем общее решение уравнения (1.35)
 . (1.37)
. (1.37)
Ясно, что (1.37) есть общий интеграл и уравнения (1.34). Выделим из него частное решение ОДУ (1.34), удовлетворяющее начальным данным  Для этого положим в (1.37)
Для этого положим в (1.37)  , тогда имеем
, тогда имеем 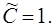 Следовательно, искомая интегральная кривая уравнения (1.34) задается уравнением
Следовательно, искомая интегральная кривая уравнения (1.34) задается уравнением
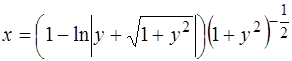 .
.
1.4.1. Примеры для самостоятельного решения
Решить следующие дифференциальные уравнения.
1. 
2. 
3. 
4. 
5. 
Решить задачу Коши.
1.  ;
;
2.  ;
;
3. 
Уравнения Бернулли
Определение. Уравнение вида
 (1.38)
(1.38)
где  – непрерывные на некотором интервале
– непрерывные на некотором интервале  функции,
функции,  действительное число, отличное от 0 и 1, называется уравнением Бернулли.
действительное число, отличное от 0 и 1, называется уравнением Бернулли.
Делением обеих частей на  и подстановкой
и подстановкой 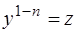 , где
, где  новая неизвестная функция, это уравнение приводится к линейному уравнению
новая неизвестная функция, это уравнение приводится к линейному уравнению
 .
.
Заметим, что при делении обеих частей уравнения (1.38) на  при
при  возможна потеря решения
возможна потеря решения  . Это решение является частным, если
. Это решение является частным, если  , и особым, если
, и особым, если  .
.
Пример 1. Решить уравнение
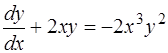 .
.
Решение. Обе части уравнения разделим на  , тогда будем иметь:
, тогда будем иметь:
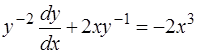 . (1.39)
. (1.39)
Положим  , откуда
, откуда  . В силу введенной подстановки уравнение (1.39) можно записать следующим образом:
. В силу введенной подстановки уравнение (1.39) можно записать следующим образом:

или
 (1.40)
(1.40)
Последнее уравнение – линейное относительно функции  . Его общее решение есть
. Его общее решение есть
 ,
,
где  произвольная константа (см. п.1.4., пример 1). Отсюда, учитывая, что
произвольная константа (см. п.1.4., пример 1). Отсюда, учитывая, что  , записываем общий интеграл исходного уравнения
, записываем общий интеграл исходного уравнения
 .
.
Так как показатель степени  в правой части нашего уравнения равен 2, то потерянное при интегрировании решение
в правой части нашего уравнения равен 2, то потерянное при интегрировании решение  является частным.
является частным.
Замечание. При интегрировании уравнения Бернулли можно также непосредственно применить подстановку  или метод вариации произвольной постоянной.
или метод вариации произвольной постоянной.
Пример 2. Проинтегрировать уравнение
 . (1.41)
. (1.41)
Решение. Уравнение (1.41) – это уравнение Бернулли. Положим  , тогда (1.41) запишется в виде
, тогда (1.41) запишется в виде
 .
.
или
 .
.
Функцию  выберем так, чтобы
выберем так, чтобы  . Например, пусть
. Например, пусть 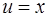 . Подставив
. Подставив  вместо
вместо  в последнее уравнение и учитывая, что
в последнее уравнение и учитывая, что  , для определения
, для определения  будем иметь уравнение
будем иметь уравнение
 . (1.42)
. (1.42)
Последнее уравнение – это уравнение с разделяющимися переменными, его общий интеграл есть
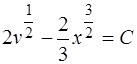 ,
,
откуда
 ,
,
где  произвольная константа. Следовательно, общее решение ОДУ (1.41) есть
произвольная константа. Следовательно, общее решение ОДУ (1.41) есть
 . (1.43)
. (1.43)
Заметим, что при интегрировании уравнения (1.42) методом разделения переменных мы теряем решение  , это ведет к потере решения
, это ведет к потере решения  уравнения (1.41). Так как в правой части (1.41) стоит степень
уравнения (1.41). Так как в правой части (1.41) стоит степень  с показателем
с показателем  , то теряемое решение является особым.
, то теряемое решение является особым.
Рассмотрим другой способ решения уравнения (1.41), а именно проинтегрируем его методом вариации произвольной постоянной. Запишем однородное уравнение, соответствующее (1.41):
 .
.
Его общее решение есть  . Пусть С= С (х), тогда общее решение (1.41) будем искать в виде
. Пусть С= С (х), тогда общее решение (1.41) будем искать в виде
 . (1.44)
. (1.44)
Подставив  и
и  в уравнение, будем иметь
в уравнение, будем иметь
 ,
,
или
 .
.
Проинтегрировав последнее уравнение, находим
 ,
,
или
 ,
,
где  произвольная константа,
произвольная константа,  . Подставляя С (х) в (1.44), получаем общее решение уравнения (1.44) в форме (1.43)
. Подставляя С (х) в (1.44), получаем общее решение уравнения (1.44) в форме (1.43)
 .
.
1.5.1. Примеры для самостоятельного решения
Решить уравнения.
1.  , 3.
, 3.  .
.
2.  ,
,
Найти решение задач Коши.
1.  ; 3.
; 3.  .
.
2.  ;
;



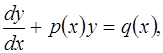 (1.28)
(1.28) – непрерывные на некотором интервале
– непрерывные на некотором интервале 
 функции.
функции.
 то уравнение (1.28) называется однородным линейным дифференциальным уравнением.
то уравнение (1.28) называется однородным линейным дифференциальным уравнением. (1.29)
(1.29) произвольная постоянная, а
произвольная постоянная, а  означает первообразную функцию для функции
означает первообразную функцию для функции  .
. уравнение (1.28) называется неоднородным. При интегрировании неоднородного линейного дифференциального уравнения (1.28) применяют так называемый метод вариации произвольной постоянной или метод Лагранжа. Этот метод состоит в том, что общее решение ОДУ (1.28) ищут в таком же виде, что и общее решение соответствующего ему однородного уравнения, т.е. в виде (1.29). Но при этом считают произвольную постоянную
уравнение (1.28) называется неоднородным. При интегрировании неоднородного линейного дифференциального уравнения (1.28) применяют так называемый метод вариации произвольной постоянной или метод Лагранжа. Этот метод состоит в том, что общее решение ОДУ (1.28) ищут в таком же виде, что и общее решение соответствующего ему однородного уравнения, т.е. в виде (1.29). Но при этом считают произвольную постоянную  непрерывно дифференцируемой функцией от
непрерывно дифференцируемой функцией от 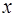 . Иллюстрацию метода проведем на следующих примерах.
. Иллюстрацию метода проведем на следующих примерах. . (1.30)
. (1.30) (1.31)
(1.31)

 (1.32)
(1.32) считаем непрерывно дифференцируемой функцией от
считаем непрерывно дифференцируемой функцией от  , т.е. в виде
, т.е. в виде . (1.33)
. (1.33)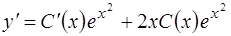 .
. из (1.33) и найденное выражение
из (1.33) и найденное выражение 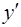 в уравнение (1.31), получаем следующее дифференциальное уравнение для определения
в уравнение (1.31), получаем следующее дифференциальное уравнение для определения  :
:
 .
.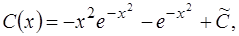 где
где  произвольная постоянная. Подставив
произвольная постоянная. Подставив 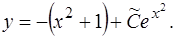
 (1.34)
(1.34) .
.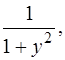 тогда будем иметь
тогда будем иметь . (1.35)
. (1.35)

 . (1.36)
. (1.36) С учетом последнего из (1.36) находим
С учетом последнего из (1.36) находим 
 .
. в (1.35), получим дифференциальное уравнение для определения
в (1.35), получим дифференциальное уравнение для определения  :
:

 ,
,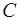 в (1.36), найдем общее решение уравнения (1.35)
в (1.36), найдем общее решение уравнения (1.35) . (1.37)
. (1.37) Для этого положим в (1.37)
Для этого положим в (1.37)  , тогда имеем
, тогда имеем 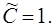 Следовательно, искомая интегральная кривая уравнения (1.34) задается уравнением
Следовательно, искомая интегральная кривая уравнения (1.34) задается уравнением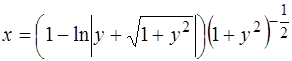 .
.




 ;
; ;
;
 (1.38)
(1.38) – непрерывные на некотором интервале
– непрерывные на некотором интервале  функции,
функции,  действительное число, отличное от 0 и 1, называется уравнением Бернулли.
действительное число, отличное от 0 и 1, называется уравнением Бернулли. и подстановкой
и подстановкой 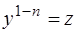 , где
, где  новая неизвестная функция, это уравнение приводится к линейному уравнению
новая неизвестная функция, это уравнение приводится к линейному уравнению .
. возможна потеря решения
возможна потеря решения  . Это решение является частным, если
. Это решение является частным, если  , и особым, если
, и особым, если  .
.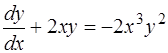 .
. , тогда будем иметь:
, тогда будем иметь: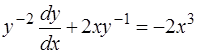 . (1.39)
. (1.39) , откуда
, откуда  . В силу введенной подстановки уравнение (1.39) можно записать следующим образом:
. В силу введенной подстановки уравнение (1.39) можно записать следующим образом:
 (1.40)
(1.40) . Его общее решение есть
. Его общее решение есть ,
, , записываем общий интеграл исходного уравнения
, записываем общий интеграл исходного уравнения .
. является частным.
является частным. или метод вариации произвольной постоянной.
или метод вариации произвольной постоянной. . (1.41)
. (1.41) .
. .
. выберем так, чтобы
выберем так, чтобы  . Например, пусть
. Например, пусть 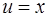 . Подставив
. Подставив  , для определения
, для определения  будем иметь уравнение
будем иметь уравнение . (1.42)
. (1.42)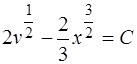 ,
, ,
, произвольная константа. Следовательно, общее решение ОДУ (1.41) есть
произвольная константа. Следовательно, общее решение ОДУ (1.41) есть . (1.43)
. (1.43) , это ведет к потере решения
, это ведет к потере решения  уравнения (1.41). Так как в правой части (1.41) стоит степень
уравнения (1.41). Так как в правой части (1.41) стоит степень  , то теряемое решение является особым.
, то теряемое решение является особым. .
. . Пусть С= С (х), тогда общее решение (1.41) будем искать в виде
. Пусть С= С (х), тогда общее решение (1.41) будем искать в виде . (1.44)
. (1.44) в уравнение, будем иметь
в уравнение, будем иметь ,
, .
. ,
, ,
, произвольная константа,
произвольная константа,  . Подставляя С (х) в (1.44), получаем общее решение уравнения (1.44) в форме (1.43)
. Подставляя С (х) в (1.44), получаем общее решение уравнения (1.44) в форме (1.43) .
. , 3.
, 3.  .
. ,
, ; 3.
; 3.  .
. ;
;