Під час розв’язування деяких задач виникла потреба добувати квадратний корінь з від’ємних чисел. Зокрема, так було під час розв’язування квадратних рівнянь з від’ємним дискримінантом.
Наприклад: 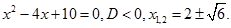
Добування кореня парного степеня з від’ємного числа неможливо, якщо обмежуватися розгляданням тільки дійсних чисел. Серед дійсних чисел немає 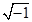 . Коренем парного степеня з від’ємного числа являються особливі (не дійсні) числа.
. Коренем парного степеня з від’ємного числа являються особливі (не дійсні) числа.
Щоб виконувалась ця операція, необхідно розширити множину дійсних чисел приєднанням до неї нових чисел так, щоб множина утворила числове поле, в якому, крім перелічених вище дій, завжди можна було виконувати і добування коренів. Це питання було успішно розв’язане лише у ХІХ ст. При розширені множини дійсних чисел повинні виконуватися такі умови:
1) визначення нових чисел повинно опиратися на поняття дійсного числа, і нова множина повинна містити всі дійсні числа;
2) для нових чисел повинно виконуватися п’ять законів перших арифметичних дій;
3) в новій числовій множині повинно мати розв’язки рівняння 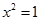 , так як в цій множині повинна виконуватися дія, обернена до піднесення до степеня, вважаючи її розв’язком цього рівняння.
, так як в цій множині повинна виконуватися дія, обернена до піднесення до степеня, вважаючи її розв’язком цього рівняння.
Домовившись 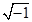 позначити буквою і і називати уявною одиницею, тобто
позначити буквою і і називати уявною одиницею, тобто 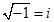 .
.
Отже, за означенням і – число, квадрат якого дорівнює -1, тобто 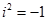 .
.
Як бачимо, що нова множина, крім дійсних чисел, містить й число і.
Розв’яжемо квадратне рівняння: 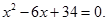
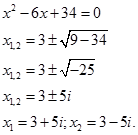
Кожен з найдених коренів представляє собою алгебраїчну суму дійсного і уявного доданків. Такі числа називаються комплексними числами.
Комплексним числом називається будь – яке число, яке має вигляд 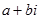 , де a і b – дійсні числа, а і – уявна одиниця.
, де a і b – дійсні числа, а і – уявна одиниця.
Оскільки в цій множині можливе множення, то вона містить і всі числа виду bi. Завжди можливе в цій множині і додавання, тому їй належать і всі числа виду 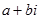 . Число а прийнято називати дійсною частиною, вираз bi – уявною частиною комплексного числа
. Число а прийнято називати дійсною частиною, вираз bi – уявною частиною комплексного числа 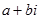 . Число b називається коефіцієнтом при уявній частині. Комплексне число позначають буквою z.
. Число b називається коефіцієнтом при уявній частині. Комплексне число позначають буквою z.
Наприклад, для комплексного числа 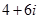 дійсною частиною є 4, а уявною – вираз 6і, коефіцієнт при уявній частині дорівнює 6, для числа
дійсною частиною є 4, а уявною – вираз 6і, коефіцієнт при уявній частині дорівнює 6, для числа 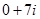 дійсною частиною є число 0, а уявною – вираз 7і, коефіцієнт при уявній частині 7.
дійсною частиною є число 0, а уявною – вираз 7і, коефіцієнт при уявній частині 7.
Із визначення комплексного числа випливає, що дійсні і уявні числа можна розглядати як окремі випадки комплексних чисел. Дійсно, в комплексному числі 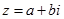 коефіцієнт
коефіцієнт 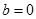 то
то 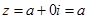 . Комплексне число стає дійсним. Якщо ж
. Комплексне число стає дійсним. Якщо ж 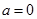 , то
, то 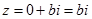 , тобто комплексне число стає чисто уявним.
, тобто комплексне число стає чисто уявним.
Поняття комплексного числа, яке ввійшло в математику ще з XVIII ст., на протязі довгого часу мало лише теоретичне значення і служило тільки потребам математики, утворюючи ряд незручностей при розв’язанні рівнянь. В науці доволі довго не було реальних явищ, які описувались би за допомогою комплексних чисел, і це призвело до того, що комплексні числа довго розглядалися як поняття, які не відповідають чому – не будь, що має місце в реальному світі. Звідси і походить термін "уявне число", тобто "реально не існуюче". Але в останній час цей погляд невірний.
Комплексне число використовується в багатьох науках: електротехніці, радіотехніці, аеродинаміці і т.д.
Із сказаного вище випливає, що комплексне число представляє корисне значення для нашої практичної діяльності розширення і узагальнення поняття числа, яке дозволяє описати важкі реальні явища, і тому являється поняттям таким же реальним, як і дійсне число.
Відносно комплексних чисел прийняті наступні властивості:
1. Два комплексних числа 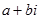 і
і 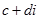 називаються рівними тоді. І тільки тоді, коли їх дійсні і уявні частини рівні і рівні коефіцієнти при уявній одиниці, тобто
називаються рівними тоді. І тільки тоді, коли їх дійсні і уявні частини рівні і рівні коефіцієнти при уявній одиниці, тобто 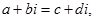 якщо
якщо 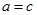 і
і 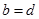 .
.
З умови рівності комплексних чисел визначимо х і у у рівнянні 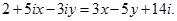
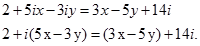
З умови рівності комплексних чисел випливає:
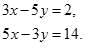
Розв’яжемо отриману систему з двох лінійних рівнянь з двома невідомими:
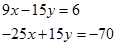
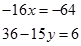
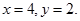
Перевірка: 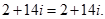
2. З умови рівності комплексних чисел виходить, що комплексне число 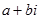 дорівнює нулю тоді, і тільки тоді, коли його дійсна частина дорівнює нулю і коефіцієнт біля уявної частини дорівнює нулю, тобто
дорівнює нулю тоді, і тільки тоді, коли його дійсна частина дорівнює нулю і коефіцієнт біля уявної частини дорівнює нулю, тобто 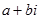 , якщо
, якщо 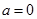 і
і 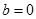 .
.
3. Модулем комплексного числа називається корінь квадратний із суми квадратів його дійсної частини і коефіцієнта біля уявної частини, тобто 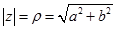 . Модуль є величина додатна, тобто яка виражає арифметичне значення кореня.
. Модуль є величина додатна, тобто яка виражає арифметичне значення кореня.
Наприклад: 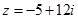 ,
, 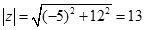 .
.
4. Два комплексних числа 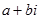 і
і 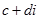 , які відрізняються лише знаком коефіцієнта біля уявної частини, називаються спряженими.
, які відрізняються лише знаком коефіцієнта біля уявної частини, називаються спряженими.
Наприклад: 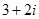 і
і 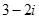 - спряжені комплексні числа.
- спряжені комплексні числа.
Комплексні корені квадратного рівняння завжди будуть спряженими числами.
Покажемо, що модулі двох спряжених чисел рівні між собою:
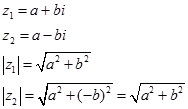
тобто 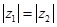 .
.
Кожне комплексне число z може бути записане у вигляді: 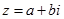 , де a і b – дійсні числа, а і – уявна одиниця. Ця форма запису комплексного числа називається алгебраїчною формою комплексного числа.
, де a і b – дійсні числа, а і – уявна одиниця. Ця форма запису комплексного числа називається алгебраїчною формою комплексного числа.
Дії над комплексними числами виконують за правилами дій над многочленами.



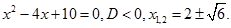
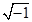 . Коренем парного степеня з від’ємного числа являються особливі (не дійсні) числа.
. Коренем парного степеня з від’ємного числа являються особливі (не дійсні) числа.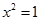 , так як в цій множині повинна виконуватися дія, обернена до піднесення до степеня, вважаючи її розв’язком цього рівняння.
, так як в цій множині повинна виконуватися дія, обернена до піднесення до степеня, вважаючи її розв’язком цього рівняння.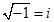 .
.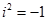 .
.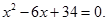
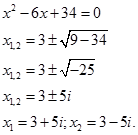
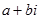 , де a і b – дійсні числа, а і – уявна одиниця.
, де a і b – дійсні числа, а і – уявна одиниця.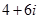 дійсною частиною є 4, а уявною – вираз 6і, коефіцієнт при уявній частині дорівнює 6, для числа
дійсною частиною є 4, а уявною – вираз 6і, коефіцієнт при уявній частині дорівнює 6, для числа 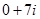 дійсною частиною є число 0, а уявною – вираз 7і, коефіцієнт при уявній частині 7.
дійсною частиною є число 0, а уявною – вираз 7і, коефіцієнт при уявній частині 7.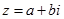 коефіцієнт
коефіцієнт 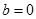 то
то 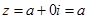 . Комплексне число стає дійсним. Якщо ж
. Комплексне число стає дійсним. Якщо ж 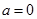 , то
, то 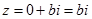 , тобто комплексне число стає чисто уявним.
, тобто комплексне число стає чисто уявним.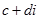 називаються рівними тоді. І тільки тоді, коли їх дійсні і уявні частини рівні і рівні коефіцієнти при уявній одиниці, тобто
називаються рівними тоді. І тільки тоді, коли їх дійсні і уявні частини рівні і рівні коефіцієнти при уявній одиниці, тобто 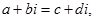 якщо
якщо 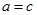 і
і 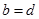 .
.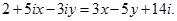
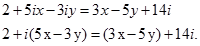
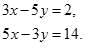
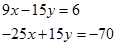
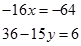
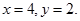
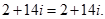
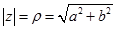 . Модуль є величина додатна, тобто яка виражає арифметичне значення кореня.
. Модуль є величина додатна, тобто яка виражає арифметичне значення кореня.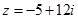 ,
, 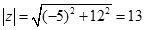 .
.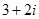 і
і 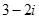 - спряжені комплексні числа.
- спряжені комплексні числа.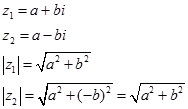
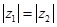 .
.


