№1.1 Найти максимальное и минимальное значения функции
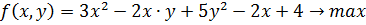
при заданных ограничениях: 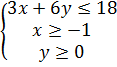 .
.
Решение:
а) Решение задачи «вручную»:
а.1) Найдём все частные производные первого порядка
 ,
, 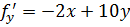 ;
;
a.2) Из одновременного равенства нулю всех частных производных
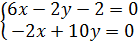 ,
, 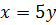 ,
,  ,
, 
получим единственную точку  , где возможен безусловный экстремум;
, где возможен безусловный экстремум;
а.3) Найдём частные производные второго порядка и вычислим их в найденной критической точке:  ,
, 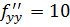 ,
,  ,
,
тогда знак выражения 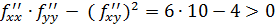 говорит о наличии экстремума в точке М. Тип экстремума даёт знак числа
говорит о наличии экстремума в точке М. Тип экстремума даёт знак числа 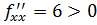 , следовательно в точке М имеется локальный безусловный минимум;
, следовательно в точке М имеется локальный безусловный минимум;
а.4) Заданная системой ограничений допустимая область является треугольником АВС, см. Рисунок 1. Все неравенства нестрогие дают замкнутость области (она содержит все точки своей границы). На этой замкнутой и ограниченной области целевая функция непрерывна, что гарантирует достижимость её наибольшего и наименьшего значений в этой области. Найденная ранее точка М попадает в эту область.
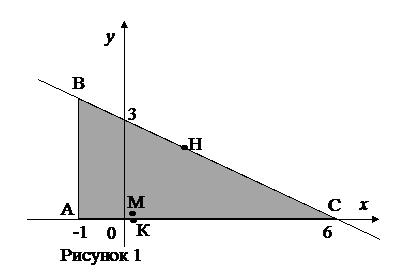
а.5) На каждом участке границы области найдём точки условного экстремума:
а.5.1) На границе АС
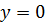 ,
, 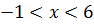 ,
,
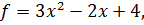
 ,
,  при
при 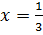 .
.
Слева от неё  , справа
, справа  , в этой точке К(
, в этой точке К(  имеется условный минимум;
имеется условный минимум;
а.5.2) На границе АВ  ,
,  ,
,

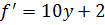 ,
,  при
при 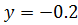 .
.
На рассмотренном промежутке  , т.е. при движении от А к В функция монотонно возрастает;
, т.е. при движении от А к В функция монотонно возрастает;
а.5.3) На границе ВС  ,
, 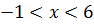 ,
,
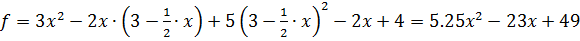 ,
,
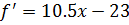 ,
,  при
при 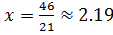 ,
,  Левее неё
Левее неё  , правее
, правее  , в этой точке Н(
, в этой точке Н( 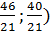 имеется условный минимум;
имеется условный минимум;
а.6) Значения функции в точках безусловного экстремума внутри области, в точках условного экстремума на её границах сравним с её значениями в угловых точках области:
 (наименьшее),
(наименьшее),
 ,
,
 ,
,
 ,
,
 ,
,
 (наибольшее).
(наибольшее).
Вывод: Наибольшее значение целевой функции при заданных ограничениях равно 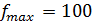 при
при 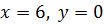 ; наименьшее значение
; наименьшее значение  при
при  ,
,  .
.
б) Эту задачу можно решить на MatCADe.
Для этого нужно задать оптимизируемую (целевую) функцию, начальные значения всех переменных и после ключевого слова Given все ограничения, после которых функцию maximize или minimize с указанием сначала названия целевой функции и после этого все изменяемые переменные. Результатом будет вектор значений этих переменных. При начальной точке О(0;0) получим:

Проблема такого метода в том, что при этом находится лишь локальный экстремум целевой функции в окрестности взятой начальной точки, который не всегда является глобальным экстремумом в заданной допустимой области. В данном случае взяв другую начальную точку Т(5;0) получим другое решение с бОльшим значением целевой функции.

Если вместе с максимизацией необходима и минимизация целевой функции, то даже при тех же ограничениях нужно снова задать начальные условия и все ограничения (целевую функцию можно снова не задавать).
Как и в случае максимизации, результат может измениться от выбора начальной точки. Взяв начальной точкой начало координат О(0;0), получим для целевой функции значение 3.667:

Взяв другую начальную точку В(1;1), получим другое условно-оптимальное значение 3.643 в её окрестности:

Ответ: 
 ,
,  .
.
Замечание 1: Чтобы уменьшить шанс нахождения не самого оптимального решения задачи, следует процедуру отыскания этого решения применять несколько раз из различных начальных точек. Для этого можно допустимую область покрыть сеткой с некоторыми шагами по первой и по второй переменной. Полученные узловые точки такой сетки берём в качестве начальных и на следующем шаге результат сравниваем с предыдущим. Выполнив процедуру в количестве узловых точек можно ожидать в результате наиболее оптимальное решение. Вместо этого можно построить карту уровней целевой функции, которая поможет исследовать её поведение и выбрать начальную точку непосредственно около точки максимума (минимума).
№1.2 В таблице при указанных значениях двух переменных заданы значения функции от этих переменных.
а) Подобрать значения параметров 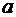 и
и  функции
функции  , чтобы она соответствовала значениям из таблицы.
, чтобы она соответствовала значениям из таблицы.
| y
x
| -0.80
| -0.60
| -0.40
| -0.20
| 0.00
| 0.20
| 0.40
| 0.60
| 0.80
| 1.00
|
| -2.00
| 27.600
| 27.200
| 26.800
| 26.400
| 26.000
| 25.600
| 25.200
| 24.800
| 24.400
| 24.000
|
| -1.50
| 16.550
| 16.350
| 16.150
| 15.950
| 15.750
| 15.550
| 15.350
| 15.150
| 14.950
| 14.750
|
| -1.00
| 8.000
| 8.000
| 8.000
| 8.000
| 8.000
| 8.000
| 8.000
| 8.000
| 8.000
| 8.000
|
| -0.50
| 1.950
| 2.150
| 2.350
| 2.550
| 2.750
| 2.950
| 3.150
| 3.350
| 3.550
| 3.750
|
| 0.00
| -1.600
| -1.200
| -0.800
| -0.400
| 0.000
| 0.400
| 0.800
| 1.200
| 1.600
| 2.000
|
| 0.50
| -2.650
| -2.050
| -1.450
| -0.850
| -0.250
| 0.350
| 0.950
| 1.550
| 2.150
| 2.750
|
| 1.00
| -1.200
| -0.400
| 0.400
| 1.200
| 2.000
| 2.800
| 3.600
| 4.400
| 5.200
| 6.000
|
| 1.50
| 2.750
| 3.750
| 4.750
| 5.750
| 6.750
| 7.750
| 8.750
| 9.750
| 10.750
| 11.750
|
| 2.00
| 9.200
| 10.400
| 11.600
| 12.800
| 14.000
| 15.200
| 16.400
| 17.600
| 18.800
| 20.000
|
| 2.50
| 18.150
| 19.550
| 20.950
| 22.350
| 23.750
| 25.150
| 26.550
| 27.950
| 29.350
| 30.750
|
б) Найти наименьшее значение функции  при найденных параметрах;
при найденных параметрах;
в) Найти наибольшее и наименьшее значения функции  и соответствующие значения переменных в области
и соответствующие значения переменных в области  , заданной условиями
, заданной условиями  . Построить чертёж фрагмента поверхности на заданной области;
. Построить чертёж фрагмента поверхности на заданной области;
Решение:
а) Из исходной таблицы заданий Word легко перенести данные копированием (Ctrl+C) в MathCAD и присвоить значения столбцов X и Y вместе с матрицей FF значений функции (для Y выполнив транспонирование).
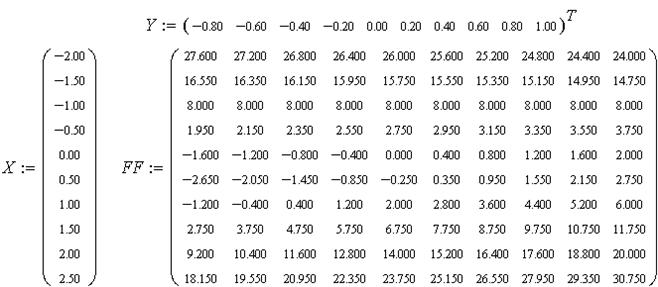
Зададим вид этой функции с двумя переменными и двумя параметрами. По ней составим вспомогательную функцию из квадратов отклонений заданных в таблице значений 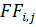 от значений предполагаемой функции
от значений предполагаемой функции  :
: 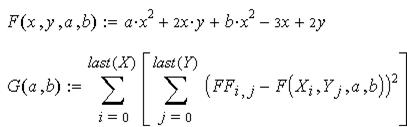 .
.
После этого при заданных начальных значениях параметров минимизировали функцию G и получили значения этих параметров, при которых получим функцию f:
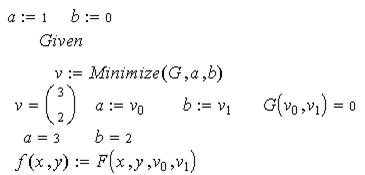
Значение G=0 говорит о полном совпадении значений полученной функции с заданными в таблице значениями.
б) При этих параметрах получили целевую функцию 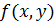 , для которой сначала найдём минимальное значение без ограничений на переменные.
, для которой сначала найдём минимальное значение без ограничений на переменные.
 Начальной точкой возьмём О(0;0) и на MathCade получим:
Начальной точкой возьмём О(0;0) и на MathCade получим:
Невозможно найти минимум этой функции, т.к. он не достигается (функция уменьшается неограниченно) в некоторых направлениях.
в) Целевую функцию  будем оптимизировать при заданных ограничениях
будем оптимизировать при заданных ограничениях  .
.
В задаче 1.1 рассмотрено решение «вручную» такого вида задач. Рассмотрим максимизацию и минимизацию при заданных ограничениях на MathCADe.
Составим вспомогательную функцию с двоичным результатом, полученным конъюнкцией всех заданных условий:
 , которая принимает значение 1 внутри допустимой области и значение 0 за её пределами. Умножение на неё целевой функции даёт
, которая принимает значение 1 внутри допустимой области и значение 0 за её пределами. Умножение на неё целевой функции даёт 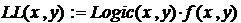 , которая за пределами допустимой области равна 0 и внутри неё равна
, которая за пределами допустимой области равна 0 и внутри неё равна  .
.
При построении её трёхмерного графика (поверхности) получим такую картину:

На Рисунке 2.а видно, что изображена не вся область и линии поверхности желательно построить погуще с добавкой цветов для сравнения их значений.
Для этого в свойствах трёхмерного графика выберем подменю Quick Plot Data, где зададим диапазоны изменений обеих переменных (например, от -5 до 7) и число ячеек сетки хотя бы 50.
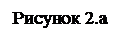
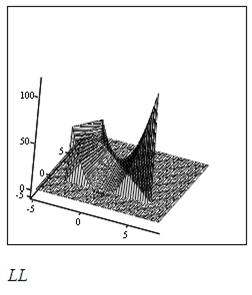
Полученный график можно поворачивать во всех направлениях, следует выбрать наиболее удачный ракурс.
Можно в подменю Специальный в части Опции контура выбрать Залить, тогда вместо сетки получим непрерывную поверхность с заливкой цветами, которые синие при малых значениях и приближаются к красным при наибольших значениях функции.
В результате получим такие поверхности:


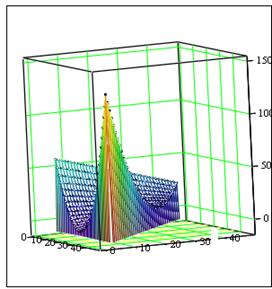
Для отыскания точек минимума и максимума этой функции можно рассмотреть другой вид графика функции двух переменных – линии уровня. Для этого в меню графика в подменю Общие выбрать Контуры коорд.

Для разноцветных линий в подменю Появление в Опции линии, Цветовые опции выбрать Палитра;
Для указания значений функции на этих линиях в подменю Специальный для Опции контура выбрать Пронумер.
По рисунку 2.д видно, что наибольшие значения принимаются у правой нижней вершины допустимой области (где имеются значения 100 и более), а наименьшие (около 0) возле середины нижней границы этой области.
Для минимизации функции возьмём начальную точку М(2, -1) и на MathCade получим:
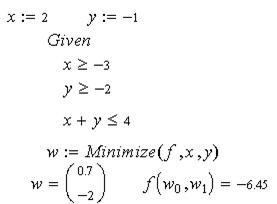 .
.
Для максимизации возьмём начальную точку К (6, 0) и на MathCade получим:

Ответ:  при которых функция не достигает наименьшего значения,
при которых функция не достигает наименьшего значения,
а в заданной области  для
для 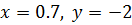 ;
;
 для
для 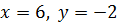 .
.
№1.3 (самостоятельно) Найти наибольшее и наименьшее значения функции
 при условиях
при условиях 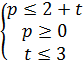 .
.
Ответ:  при t=0.5, p=0;
при t=0.5, p=0;  при t=3, p=5.
при t=3, p=5.
№1.4 В таблице указаны расходы трёх видов сырья при производстве двух видов продукции, запасы сырья и прибыль от реализации продукции.
| Сырьё
| Расход (кг) на единицу продукции
| Запас (кг)
|
| А
| В
|

| 1
| 3
| 180
|

| 2
| 2
| 160
|
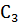
| 4
| 2
| 240
|
| Прибыль от единицы (ден.)
| 4
| 3
|
|
а) Найти оптимальный план выпуска этих изделий с максимально возможной прибылью от их реализации (допуская дробные значения и обеспеченным сбытом).
б) Сформулировать двойственную задачу и найти оптимальные оценки каждого сырья.
в) Найти оптимальный план производства и изменение общей прибыли при увеличении С1 на 1 кг, уменьшении С2 на 2 кг, увеличении С3 на 3 кг в.1) по отдельности в.2) одновременно (если при этом не изменятся оптимальные двойственные оценки);
г) Пусть прибыль является функцией от параметра t, при производстве единицы А составляет п1=4+t , а для единицы В п2=3-2t. Найти оптимальный план производства изделий А и В и наибольшую прибыль при каждом значении параметра t.
Решение:
а) Оптимальный план выпуска.
а.1) Математическая модель задачи (основная ЗЛП).
Пусть  – число выпущенных единиц продукции А,
– число выпущенных единиц продукции А,  – число единиц продукции В. Тогда прибыль от А составит
– число единиц продукции В. Тогда прибыль от А составит 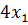 , от В она
, от В она  и общая прибыль
и общая прибыль  , которая максимизируется.
, которая максимизируется.
Сырья  для А потребуется
для А потребуется  и для В
и для В  , что в сумме не должно превосходить его запас 180 кг. Получили первое ограничение. По сырью
, что в сумме не должно превосходить его запас 180 кг. Получили первое ограничение. По сырью  и
и 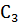 получим второе и третье ограничения. К ним добавим условие неотрицательности значений
получим второе и третье ограничения. К ним добавим условие неотрицательности значений  и
и  .
.
Получили основную задачу линейного программирования:
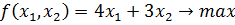
 ;
;
а.2) Графический метод решения ЗЛП.
а.2.1) Область допустимых решений.
Условие  в плоскости
в плоскости 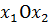 задаёт полуплоскость с границей
задаёт полуплоскость с границей  - прямая линия с пересечением осей при
- прямая линия с пересечением осей при  и
и  , содержащую начало координат (т.к. неравенство
, содержащую начало координат (т.к. неравенство  верное);
верное);  задаёт полуплоскость с границей
задаёт полуплоскость с границей  - прямая линия с пересечением осей при
- прямая линия с пересечением осей при  и
и  , содержащую начало 24
, содержащую начало 24  - прямая линия с пересечением осей при
- прямая линия с пересечением осей при 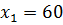 и
и 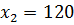 , содержащую начало координат. Условия
, содержащую начало координат. Условия  дают точки из I координатной четверти.
дают точки из I координатной четверти.
Пересечение этих областей даёт допустимую область (область допустимых решений) – пятиугольник ОАВСD на Рисунке 6;
а.2.2) Направление наибольшего возрастания.
Коэффициенты целевой функции дают вектор  , который является градиентом этой функции и в его направлении функция имеет наибольшую скорость возрастания. В направлении этого вектора проведём из начала координат луч (на Рисунке 6 изображен пунктиром). Перпендикулярно к этому лучу построим прямые
, который является градиентом этой функции и в его направлении функция имеет наибольшую скорость возрастания. В направлении этого вектора проведём из начала координат луч (на Рисунке 6 изображен пунктиром). Перпендикулярно к этому лучу построим прямые  , которые являются линиями уровня целевой функции и в точках одной такой прямой постоянно значение
, которые являются линиями уровня целевой функции и в точках одной такой прямой постоянно значение 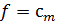 . Перемещая такие прямые в направлении градиента получим увеличение значений функции
. Перемещая такие прямые в направлении градиента получим увеличение значений функции  ;
;
а.2.3) Оптимальное решение основной задачи.
Точка области, после которой линии уровня не имеют общих точек с допустимой областью, является точкой оптимума и её координаты являются решением задачи оптимизации. Здесь точкой оптимума является точка С (см. Рисунок 3), которая является пересечением границ ВС и CD и координаты которой даёт система уравнений этих прямых.
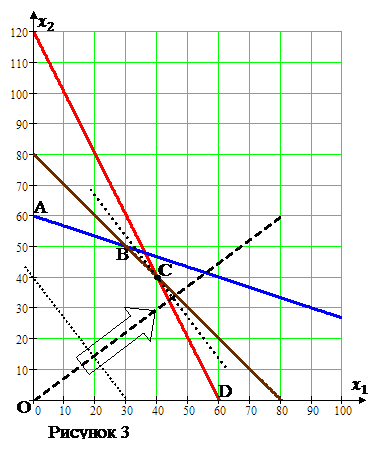
 ,
,

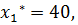
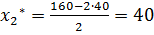 ,
,

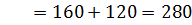 ден.
ден.
б) Двойственные оценки сырья.
б.1) Для основной ЗЛП 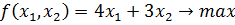

двойственной ЗЛП будет: 
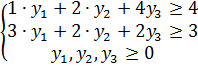 ,
,
где
· Число переменных равно числу исходных ограничений (видов сырья);
· Новая целевая функция минимизируется, её коэффициенты – неоднородности исходной системы (запасы сырья);
· В новой системе ограничений коэффициенты  и её матрица получена транспонированием матрицы исходной системы;
и её матрица получена транспонированием матрицы исходной системы;
· Неоднородности (правые части) являются коэффициентами исходной целевой функции (прибылями от продукции);
· При неотрицательности исходной переменной соотв. ограничение имеет вид неравенства вида  (равенством при любом знаке переменной);
(равенством при любом знаке переменной);
· Переменная неотрицательна при исходном ограничении с таким номером в виде неравенства (может принимать любой знак при исходном уравнении).
Теорема о двойственности говорит, что если из двойственной пары ЗЛП одна имеет единственное оптимальное решение, то и другая тоже имеет единственное оптимальное решение и выполнено  .
.
Если бы в задаче было 2 вида сырья, и двойственная имела две переменные, то и двойственная задача могла быть решена графически. После построения допустимой области и направления градиента целевой функции нужно было бы передвигать линию уровня в противоположном ему направлении до точки оптимума, дальнейший переход от которой перестанет давать общие точки с допустимой областью.
В данном случае двойственная задача имеет три переменные, её хотя и можно решить графически, но проще симплекс-методом.
б.2) В общем случае оптимальные решения обеих задач двойственной пары можно найти симплекс-методом.
Для основной ЗЛП 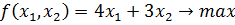

от канонического вида с ограничениями-неравенствами перейдём к нормальному виду с ограничениями-уравнениями. Для этого в каждом неравенстве к левой части прибавим новую неотрицательную переменную – остаток такого сырья.
Получим 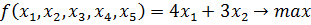
 .
.
По этой задаче составим первую симплекс-таблицу:
· Заполним три первых строки столбцов коэффициентов при x1, x 2, x 3, x 4, x 5, Р0 – столбец неоднородности;
· Над столбцами укажем коэффициенты Сi исходной целевой функции при таких переменных;
· Единичные столбцы дают базис на этом шаге - x 3, x 4, x 5;
· В столбце Сбазис укажем элементы строки С при базисных переменных этого шага;
· В последней строке укажем коэффициенты целевой функции с противоположными знаками.
Метод состоит из нескольких шагов. На каждом шаге после заполнения таблицы находим опорное решение и для него значение целевой функции: Значения базисных переменных дают первые элементы столбца Ро при значениях 0 остальных переменных, значение f даёт последний элемент столбцаРо.
1 шаг) Начальное опорное решение Х0=(0,0,180,160,240) и f =0. Первые две координаты дают вершину О(0;0) допустимой области из геометрического метода решения. Такое решение оптимальным не является, т.к. в последней строке матрицы имеются отрицательные элементы -4 и -3. Максимальный модуль из них в 1-м столбце, тогда в базисный набор следует включить x1; В столбце этого значения для положительных элементов найдём наименьшее отношение к ним элементов Ро  в строке III с базисной
в строке III с базисной 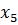 , тогда в базисе
, тогда в базисе 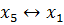 .
.
| №
|
Базис
| Сбазис
| Ро
| 4
| 3
| 0
| 0
| 0
|
| x 1
| x 2
| x 3
| x 4
| x 5
|
| I
| x 3
| 0
| 180
| 1
| 3
| 1
| 0
| 0
|
| II
| x 4
| 0
| 160
| 2
| 2
| 0
| 1
| 0
|
| III
| x 5
| 0
| 240
| 4
| 2
| 0
| 0
| 1
|
| IV
| f
| -
| 0
| -4
| -3
| 0
| 0
| 0
|
| I
| x 3
| 0
| 120
| 0
| 2.5
| 1
| 0
| -0.25
|
| II
| x 4
| 0
| 40
| 0
| 1
| 0
| 1
| -0.5
|
| III
| x 1
| 4
| 60
| 1
| 0.5
| 0
| 0
| 0.25
|
| IV
| f
| -
| 240
| 0
| -1
| 0
| 0
| 1
|
| I
| x 3
| 0
| 20
| 0
| 0
| 1
| -2.5
| 1
|
| II
| x 2
| 3
| 40
| 0
| 1
| 0
| 1
| -0.5
|
| III
| x 1
| 4
| 40
| 1
| 0
| 0
| -0.5
| 0.5
|
| IV
| f
| -
| 280
| 0
| 0
| 0
| 1
| 0.5
|
|
|
Для этого по методу Гаусса по строкам выполним:
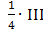 ,
,  ,
,
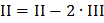 ,
, 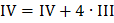
2 шаг) Х1=(60,0,120,40,0)
(точка D(60;0) допуст.обл.)
f1=240 не оптимально. Во втором столбце получим 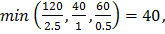
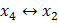
по методу Гаусса:
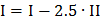 ,
, 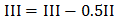 ,
, 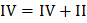
3 шаг) В последней строке нет отрицательных элементов, тогда решение Х3=(40,40,20,0,0) (точка С(40;40) допустимой области) является оптимальным и 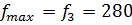 .
.
На MathCADe симплекс метод можно реализовать так:
Для этого можно написать программу, по которой выполняется пересчёт матрицы с указанным разрешающим элементом (номерами его строки и столбца) и получением на месте выбранного столбца единичный столбец:
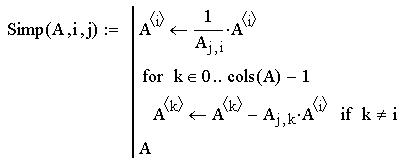 .
.
Зададим матрицу А – первую симплекс-таблицу. В ней смотрим элементы последней строки: если отрицательных элементов нет, то найдено оптимальное решение. Если в этой строке имеются отрицательные элементы, то опорное решение не оптимально и следует методом Гаусса преобразовать матрицу А.

Сначала в матрице А взят разрешающим элемент  c уменьшением на 1 каждого индекса; Для полученной матрицы А1 взят разрешающим
c уменьшением на 1 каждого индекса; Для полученной матрицы А1 взят разрешающим  . В полученной матрице А2 последняя строка не содержит отрицательных элементов, найдено оптимальное решение основной и двойственной задач.
. В полученной матрице А2 последняя строка не содержит отрицательных элементов, найдено оптимальное решение основной и двойственной задач.
б.3) Оптимальные оценки сырья и их анализ.
б.3.1) При решении симплекс-методом найдено оптимальное решение и двойственной задачи. Его элементы записаны в последней строке последней матрицы в столбцах, которые на первом шаге были базисными. В данном случае ими являлись столбцы переменных x 3, x 4, x 5 где получим оптимальные оценки сырья:  .
.
Они говорят, что небольшие изменения запаса сырья С1 не приведут к изменению максимальной прибыли от производства изделий А и В; Увеличение запаса С2 на свою единицу (на 1 кг) приведёт к увеличению максимальной прибыли на  ден.; Увеличение запаса С3 на свою единицу (на 1 кг) приведёт к увеличению максимальной прибыли на
ден.; Увеличение запаса С3 на свою единицу (на 1 кг) приведёт к увеличению максимальной прибыли на 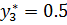 ден. Если цена этих видов сырья одинакова и можно изменять только один запас, то выгоднее увеличивать запас С2. Если допустимо изменять несколько запасов, то изменение максимальной прибыли даёт выражение
ден. Если цена этих видов сырья одинакова и можно изменять только один запас, то выгоднее увеличивать запас С2. Если допустимо изменять несколько запасов, то изменение максимальной прибыли даёт выражение 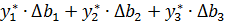 при сохранении структуры решения основной задачи. Для этого в матрице последней таблицы из столбцов, которые на начальном шаге были базисными, составим матрицу
при сохранении структуры решения основной задачи. Для этого в матрице последней таблицы из столбцов, которые на начальном шаге были базисными, составим матрицу  .
.
б.3.2) Новое оптимальное решение основной задачи станет
 , если все его составляющие останутся неотрицательными.
, если все его составляющие останутся неотрицательными.
Например, если первый запас увеличим на 2 кг, второй запас уменьшим на 1 кг и третий увеличим на 3 кг, то получим

т.е. при новых запасах структура решения не изменится и следует производить 42 единицы А и 37.5 единиц В. При этом ранее полученная прибыль 280 изменится на величину  ден. и составит 280.5 ден.;
ден. и составит 280.5 ден.;
в) Оптимальные решения при зависимости прибыли от параметра.
Пусть прибыль является функцией от параметра t: при производстве единицы А составляет п1=4+t ден., а для В она п2=3-2t ден..
Заметим, что ранее решена задача при t =0. Анализ оптимального решения при всех значениях параметра можно в случае двух переменных выполнять графически (см. Рисунок 6):
в.1) При увеличении параметра при t >0 вектор-градиент целевой функции 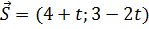 , будет поворачиваться вокруг начала координат по ходу часовой стрелки. Сначала точкой оптимума останется вершина С(40;40) допустимой области и
, будет поворачиваться вокруг начала координат по ходу часовой стрелки. Сначала точкой оптимума останется вершина С(40;40) допустимой области и  .
.
Это будет продолжаться до тех пор, пока вектор  не станет перпендикулярным к прямой CD:
не станет перпендикулярным к прямой CD:  и не станет её нормальным вектором. Это произойдёт после
и не станет её нормальным вектором. Это произойдёт после 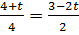 ,
, 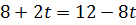 ,
, 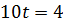 ,
,  ;
;
в.2) При  получим множество оптимальных решений, образующих отрезок CD, т.е. при выполнении
получим множество оптимальных решений, образующих отрезок CD, т.е. при выполнении 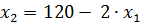 ,
, 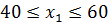 ;
;
 ;
;
в.3) При 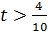 точкой оптимума становится
точкой оптимума становится  ,
,
 ;
;
Точка D перестанет быть точкой оптимума, когда вектор  станет перпендикулярным к прямой CО, т.е. при t >0 его первая координата станет нулевой, что невозможно. Тогда при любом
станет перпендикулярным к прямой CО, т.е. при t >0 его первая координата станет нулевой, что невозможно. Тогда при любом 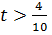 оптимальное решение
оптимальное решение 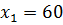 ,
, 
 ;
;
в.4) При уменьшении параметра от t =0 вершина С перестанет быть точкой оптимума, когда вектор  станет перпендикулярным к прямой ВС:
станет перпендикулярным к прямой ВС:
 и не станет её нормальным вектором. Это произойдёт при
и не станет её нормальным вектором. Это произойдёт при  ,
,  ,
, 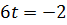 ,
,  . Тогда С является единственной точкой оптимума при
. Тогда С является единственной точкой оптимума при 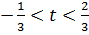 ,
,

в.5) При  получим множество оптимальных решений, образующих отрезок ВС, т.е. при выполнении
получим множество оптимальных решений, образующих отрезок ВС, т.е. при выполнении  ,
,  ;
;
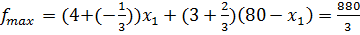 ;
;
в.6) При уменьшении параметра от t = 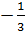 вершина В перестанет быть точкой оптимума, когда вектор
вершина В перестанет быть точкой оптимума, когда вектор  станет перпендикулярным к прямой АВ:
станет перпендикулярным к прямой АВ:
 и не станет её нормальным вектором. Это произойдёт при
и не станет её нормальным вектором. Это произойдёт при 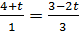 ,
,  ,
,  ,
,  .
.
Тогда В(30;50) является единственной точкой оптимума при  ,
,

в.7) При 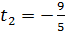 получим множество оптимальных решений, образующих отрезок АВ, т.е. при выполнении
получим множество оптимальных решений, образующих отрезок АВ, т.е. при выполнении  ,
,  ;
;
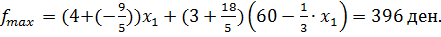 ;
;
в.8) При уменьшении параметра от t =  точкой оптимума станет вершина А(0;60),
точкой оптимума станет вершина А(0;60), 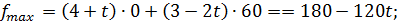
Она перестанет быть точкой оптимума, когда вектор  станет перпендикулярным к прямой ОА: т.е. при t <
станет перпендикулярным к прямой ОА: т.е. при t <  его вторая координата
его вторая координата 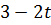 станет нулевой, что невозможно. Тогда А является единственной точкой оптимума при
станет нулевой, что невозможно. Тогда А является единственной точкой оптимума при  .
.
Совокупность результатов п. в.1 – в.8 покажем на рисунке 4 и в Таблице 2.
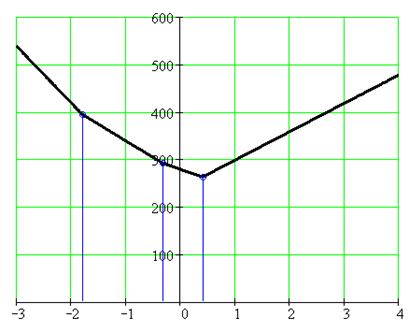
Рисунок 4 Зависимость максимальной прибыли от двух видов продукции с изменением параметра t от -3 до 4.
Таблица 2 Оптимальные решения основной ЗЛП при различных значениях
параметра t
Ответ: а) При заданных запасах сырья следует производить 40 единиц продукции А и 40 единиц В, при этом максимально возможная прибыль составит 280 ден.;
б) Оптимальные оценки сырья  . При
. При  и
и 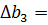 3 кг структура оптимального решения не изменится и следует произвести 42 единицы
3 кг структура оптимального решения не изменится и следует произвести 42 единицы



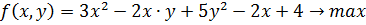
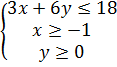 .
. ,
, 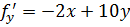 ;
;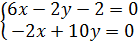 ,
, 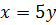 ,
,  ,
, 
 , где возможен безусловный экстремум;
, где возможен безусловный экстремум; ,
, 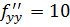 ,
,  ,
,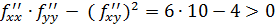 говорит о наличии экстремума в точке М. Тип экстремума даёт знак числа
говорит о наличии экстремума в точке М. Тип экстремума даёт знак числа 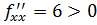 , следовательно в точке М имеется локальный безусловный минимум;
, следовательно в точке М имеется локальный безусловный минимум;
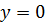 ,
, 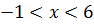 ,
,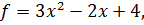
 ,
,  при
при 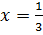 .
. , справа
, справа  , в этой точке К(
, в этой точке К(  имеется условный минимум;
имеется условный минимум; ,
,  ,
,
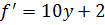 ,
, 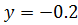 .
. ,
, 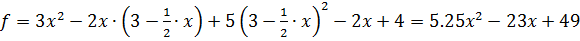 ,
,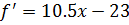 ,
, 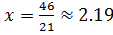 ,
,  Левее неё
Левее неё 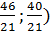 имеется условный минимум;
имеется условный минимум; (наименьшее),
(наименьшее), ,
, ,
, ,
, ,
, (наибольшее).
(наибольшее).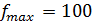 при
при 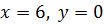 ; наименьшее значение
; наименьшее значение  при
при  ,
,  .
.




 ,
, 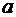 и
и  функции
функции  , чтобы она соответствовала значениям из таблицы.
, чтобы она соответствовала значениям из таблицы. при найденных параметрах;
при найденных параметрах; , заданной условиями
, заданной условиями  . Построить чертёж фрагмента поверхности на заданной области;
. Построить чертёж фрагмента поверхности на заданной области;
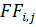 от значений предполагаемой функции
от значений предполагаемой функции  :
: 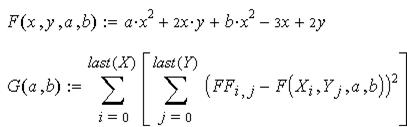 .
.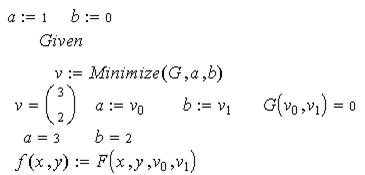
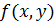 , для которой сначала найдём минимальное значение без ограничений на переменные.
, для которой сначала найдём минимальное значение без ограничений на переменные. Начальной точкой возьмём О(0;0) и на MathCade получим:
Начальной точкой возьмём О(0;0) и на MathCade получим: будем оптимизировать при заданных ограничениях
будем оптимизировать при заданных ограничениях  , которая принимает значение 1 внутри допустимой области и значение 0 за её пределами. Умножение на неё целевой функции даёт
, которая принимает значение 1 внутри допустимой области и значение 0 за её пределами. Умножение на неё целевой функции даёт 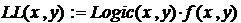 , которая за пределами допустимой области равна 0 и внутри неё равна
, которая за пределами допустимой области равна 0 и внутри неё равна  .
.
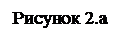





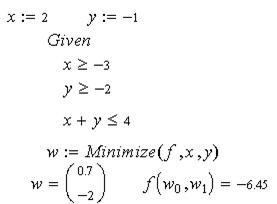 .
.
 при которых функция не достигает наименьшего значения,
при которых функция не достигает наименьшего значения,  для
для 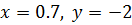 ;
; для
для 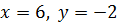 .
. при условиях
при условиях 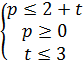 .
. при t=0.5, p=0;
при t=0.5, p=0;  при t=3, p=5.
при t=3, p=5. 

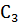
 – число выпущенных единиц продукции А,
– число выпущенных единиц продукции А,  – число единиц продукции В. Тогда прибыль от А составит
– число единиц продукции В. Тогда прибыль от А составит 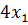 , от В она
, от В она  и общая прибыль
и общая прибыль  , которая максимизируется.
, которая максимизируется. и для В
и для В 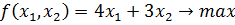
 ;
; в плоскости
в плоскости 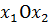 задаёт полуплоскость с границей
задаёт полуплоскость с границей  - прямая линия с пересечением осей при
- прямая линия с пересечением осей при  и
и  , содержащую начало координат (т.к. неравенство
, содержащую начало координат (т.к. неравенство  верное);
верное);  задаёт полуплоскость с границей
задаёт полуплоскость с границей  и
и  , содержащую начало 24
, содержащую начало 24  - прямая линия с пересечением осей при
- прямая линия с пересечением осей при 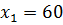 и
и 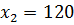 , содержащую начало координат. Условия
, содержащую начало координат. Условия  дают точки из I координатной четверти.
дают точки из I координатной четверти. , который является градиентом этой функции и в его направлении функция имеет наибольшую скорость возрастания. В направлении этого вектора проведём из начала координат луч (на Рисунке 6 изображен пунктиром). Перпендикулярно к этому лучу построим прямые
, который является градиентом этой функции и в его направлении функция имеет наибольшую скорость возрастания. В направлении этого вектора проведём из начала координат луч (на Рисунке 6 изображен пунктиром). Перпендикулярно к этому лучу построим прямые  , которые являются линиями уровня целевой функции и в точках одной такой прямой постоянно значение
, которые являются линиями уровня целевой функции и в точках одной такой прямой постоянно значение 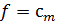 . Перемещая такие прямые в направлении градиента получим увеличение значений функции
. Перемещая такие прямые в направлении градиента получим увеличение значений функции  ;
;
 ,
,
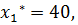
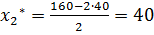 ,
,
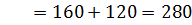 ден.
ден.
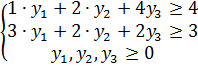 ,
,  и её матрица получена транспонированием матрицы исходной системы;
и её матрица получена транспонированием матрицы исходной системы; (равенством при любом знаке переменной);
(равенством при любом знаке переменной); .
.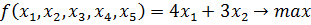
 .
. в строке III с базисной
в строке III с базисной 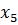 , тогда в базисе
, тогда в базисе 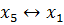 .
.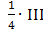 ,
,  ,
,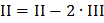 ,
, 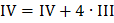
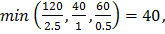
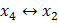
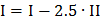 ,
, 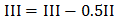 ,
, 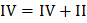
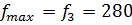 .
.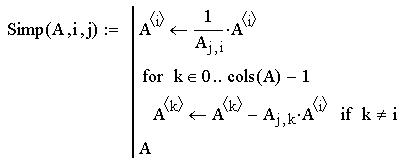 .
.
 c уменьшением на 1 каждого индекса; Для полученной матрицы А1 взят разрешающим
c уменьшением на 1 каждого индекса; Для полученной матрицы А1 взят разрешающим  . В полученной матрице А2 последняя строка не содержит отрицательных элементов, найдено оптимальное решение основной и двойственной задач.
. В полученной матрице А2 последняя строка не содержит отрицательных элементов, найдено оптимальное решение основной и двойственной задач. .
. ден.; Увеличение запаса С3 на свою единицу (на 1 кг) приведёт к увеличению максимальной прибыли на
ден.; Увеличение запаса С3 на свою единицу (на 1 кг) приведёт к увеличению максимальной прибыли на 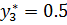 ден. Если цена этих видов сырья одинакова и можно изменять только один запас, то выгоднее увеличивать запас С2. Если допустимо изменять несколько запасов, то изменение максимальной прибыли даёт выражение
ден. Если цена этих видов сырья одинакова и можно изменять только один запас, то выгоднее увеличивать запас С2. Если допустимо изменять несколько запасов, то изменение максимальной прибыли даёт выражение 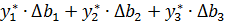 при сохранении структуры решения основной задачи. Для этого в матрице последней таблицы из столбцов, которые на начальном шаге были базисными, составим матрицу
при сохранении структуры решения основной задачи. Для этого в матрице последней таблицы из столбцов, которые на начальном шаге были базисными, составим матрицу  .
. , если все его составляющие останутся неотрицательными.
, если все его составляющие останутся неотрицательными.
 ден. и составит 280.5 ден.;
ден. и составит 280.5 ден.;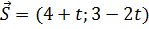 , будет поворачиваться вокруг начала координат по ходу часовой стрелки. Сначала точкой оптимума останется вершина С(40;40) допустимой области и
, будет поворачиваться вокруг начала координат по ходу часовой стрелки. Сначала точкой оптимума останется вершина С(40;40) допустимой области и  .
. не станет перпендикулярным к прямой CD:
не станет перпендикулярным к прямой CD:  и не станет её нормальным вектором. Это произойдёт после
и не станет её нормальным вектором. Это произойдёт после 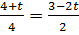 ,
, 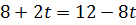 ,
, 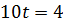 ,
,  ;
; получим множество оптимальных решений, образующих отрезок CD, т.е. при выполнении
получим множество оптимальных решений, образующих отрезок CD, т.е. при выполнении 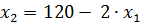 ,
, 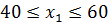 ;
; ;
;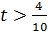 точкой оптимума становится
точкой оптимума становится  ,
, ;
;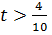 оптимальное решение
оптимальное решение 
 ;
; и не станет её нормальным вектором. Это произойдёт при
и не станет её нормальным вектором. Это произойдёт при  ,
,  ,
, 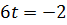 ,
,  . Тогда С является единственной точкой оптимума при
. Тогда С является единственной точкой оптимума при 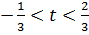 ,
, 
 получим множество оптимальных решений, образующих отрезок ВС, т.е. при выполнении
получим множество оптимальных решений, образующих отрезок ВС, т.е. при выполнении  ,
,  ;
;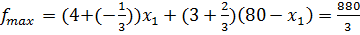 ;
;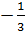 вершина В перестанет быть точкой оптимума, когда вектор
вершина В перестанет быть точкой оптимума, когда вектор 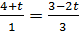 ,
,  ,
,  ,
,  .
. ,
, 
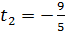 получим множество оптимальных решений, образующих отрезок АВ, т.е. при выполнении
получим множество оптимальных решений, образующих отрезок АВ, т.е. при выполнении  ,
,  ;
;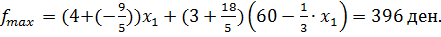 ;
; точкой оптимума станет вершина А(0;60),
точкой оптимума станет вершина А(0;60), 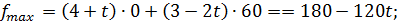
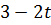 станет нулевой, что невозможно. Тогда А является единственной точкой оптимума при
станет нулевой, что невозможно. Тогда А является единственной точкой оптимума при  .
.




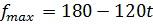
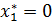
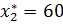






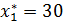

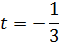


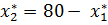
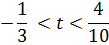
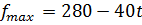
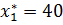
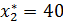
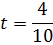



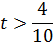


 и
и 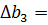 3 кг структура оптимального решения не изменится и следует произвести 42 единицы
3 кг структура оптимального решения не изменится и следует произвести 42 единицы 


