

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...
Топ:
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Интересное:
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Пусть X и Y – два допустимых решения. Говорят, что Х доминирует Y, если для всех I= 1,2,….n выполнятся неравенство fi (X) ≥ fi (Y) и найдется такое k, что fk(X)>fk(Y).
Решение Z называется недоминируемым (эффективным), если нет решения Х, которое бы доминировало Z.
Множество эффективных (недоминируемых) решений называется множеством Парето. Геометрическое изображение множества Парето называется Парето-эффективной границей (Парето-оптимальной границей)
Метод построения Парето-оптимальной границы.
1) Строим допустимое множество D, заданной системой ограничений как пересечение полуплоскостей, соответствующих каждому неравенству, входящему в эту систему.
2) Для каждой функции fi = ci1x1+ ci2x2+ cio строим линию уровня как прямую, перпендикулярную соответствующему вектору нормали n i = (ci1,сi2 ). Каждая из этих линий уровня разбивает плоскость XOY на две полуплоскости. Пусть Пi – полуплоскости, содержащие вектор градиента целевой функции fi, а их пересечения : n
П= Ç Пi;
i=1
3) Перемещая данную область П по границе допустимого множества D, находим те точки границы, которые являются единственными точками пересечения областей П и D. Данные точки являются оптимальными по Парето, а множество всех таких точек – Парето –эффективной границей.
Методы решения задач многокритериальной оптимизации – метод приоритетов.
Метод приоритетов решения многокритериальных задач применяется в том случае, когда критерии fi упорядочены по их относительной важности.
На первом шаге решения задачи отбирают множество исходов, которые имеют максимальную оценку по важнейшему критерию. Если исход единственный, то он и является оптимальным. Если же исходов несколько, то среди них выбирают те, которые имеют максимальную оценку по второму по важности критерию. Если опять исходов несколько, то процесс повторяют для следующих критерий.
|
|
Методы решения задач многокритериальной оптимизации – метод обобщенного критерия (метод свертки).
Метод перехода от нескольких критериев f1, f2, …fm к одному, задаваемому новой функцией : m
z = å (aj*fj)
j=1
называется сверткой, или методом обобщенного критерия. Числа aj называются весовыми коэффициентами. Чем больше aj, тем больший «вклад» вносит j-й
m
критерий в обобщенный критерий z. Иногда требуют, чтобы åaj = 1
j=1
18. Методы решения задач многокритериальной оптимизации – метод идеальной точки.
Метод идеальной точки является «геометрическим» методом для многокритериальных задач.
Метод идеальной точки — в области допустимых значений неизвестных ищется такая их совокупность, которая способна обеспечить набор значений критериев, в том или ином смысле ближайших к наилучшему, как правило, недосягаемому (в так называемой точке утопии).
19. Основные понятия в игровых моделях: стратегии, матрица выигрышей.
Стратегией игрока называется совокупность правил, опреде-ляющих поведение игрока на каждом ходе в зависимости от сложив-шейся ситуации.
Оптимальная стратегия игрока обеспечивает ему при много-кратном повторении игры максимально возможный выигрыш.
Парная игра, в которой выигрыш одного из игроков равен проигрышу другого, называется антагонистической или игрой с нулевой суммой.
|
|
а11 а12 ….. а1n
а21 а22 ….. а2n
Матрица … ….. …. ….
аm1 аm2 …. amn
называется платежной матрицей или матрицей выйгрышей.
Принцип максимина и минимакса, верхняя и нижняя цена игры, седловая точка, оптимальные стратегии, цена игры.
Максимин означает, что нижняя цена игры определяет минимальный выигрыш участника. Минимакс означает, что верхняя цена игры определяет максимальный проигрыш участника
Пусть ai – наименьший выигрыш игрока А при выборе им стратегии Аi для всех возможных стратегий игрока В, ai = min aij. Тогда гарантированный выигрыш
j=1,n
игрока А при любой стратегии игрока В равен:
a= max ai = max min aij.
i=1,m i=1,m j=1,n
Число a называется нижней ценой игры.
Число b = min max aij называется верхней ценой игры. Это гарантированный
j=1,n i=1,m
проигрыш игрока В.
Если a=b=n, то n называется чистой ценой (ценой игры), а пара чистых оптимальных стратегий Аi и Bj, для которой aij =n, называется седловой точкой матрицы.
Стратегия игрока называется оптимальной, если при многократном повторении игры она обеспечивает игроку максимально возможный средний выигрыш (минимально возможный средний проигрыш).
Доминируемые стратегии.
Если в платежной матрице Р все элементы i –й строки не меньше соответствующих элементов k-й строки, а aij ≥akj, j=1,n, а по крайней мере один строго больше, то
i-я строка называется доминирующей, а k-я строка доминируемой.
22. Решение игр в смешанных стратегиях.
Если a<b, то применение чистых стратегий не дает оптимального решения игры. Его можно получить случайным образом чередуя чистые стратегии, т.е в смешанных стратегиях.
ОПРЕДЕЛЕНИЕ: Смешанной стратегией SА игрока А называется применение
m
чистых стратегий А1,А2,….., Аm с вероятностями p1,p2,…..,pm, åpi = 1.
i=1
SА = А1 А2 … Аm
P1 P2 … Pm
Аналогично для игрока В:
|
|
B1 B2 … Bn n
SB = q1 q2 … qn , å qj=1
j=1
ТЕОРЕМА НЕЙМАНА: Каждая конечная игра имеет, по крайней мере, одно оптимальное решение, возможно, среди смешанных стратегий.
23. Графическое решение игр вида 2 * n и m * 2.
У таких игр всегда имеется решение, содержащее не более двух активных стратегий для каждого из игроков. Если найти эти активные стратегии, то игра 2 х n или m х 2 сводится к игре 2 х 2.
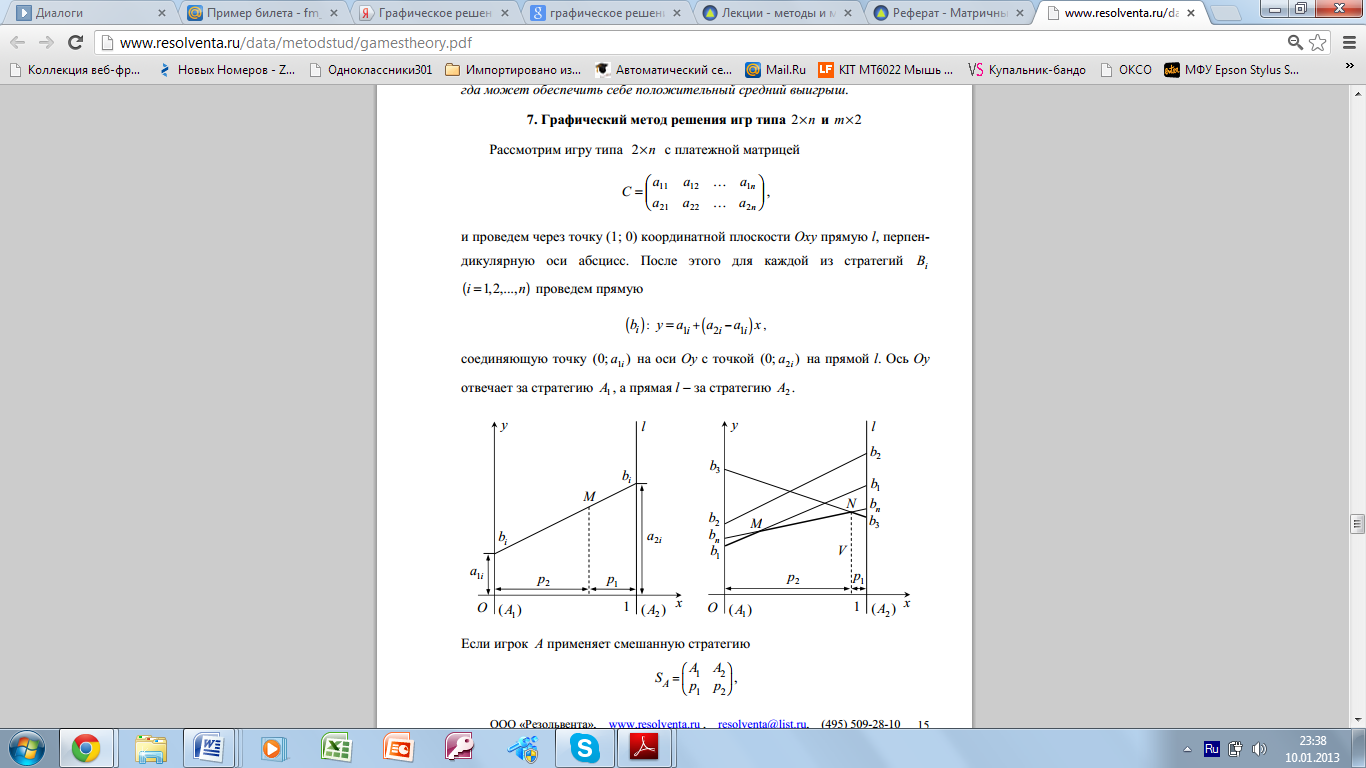
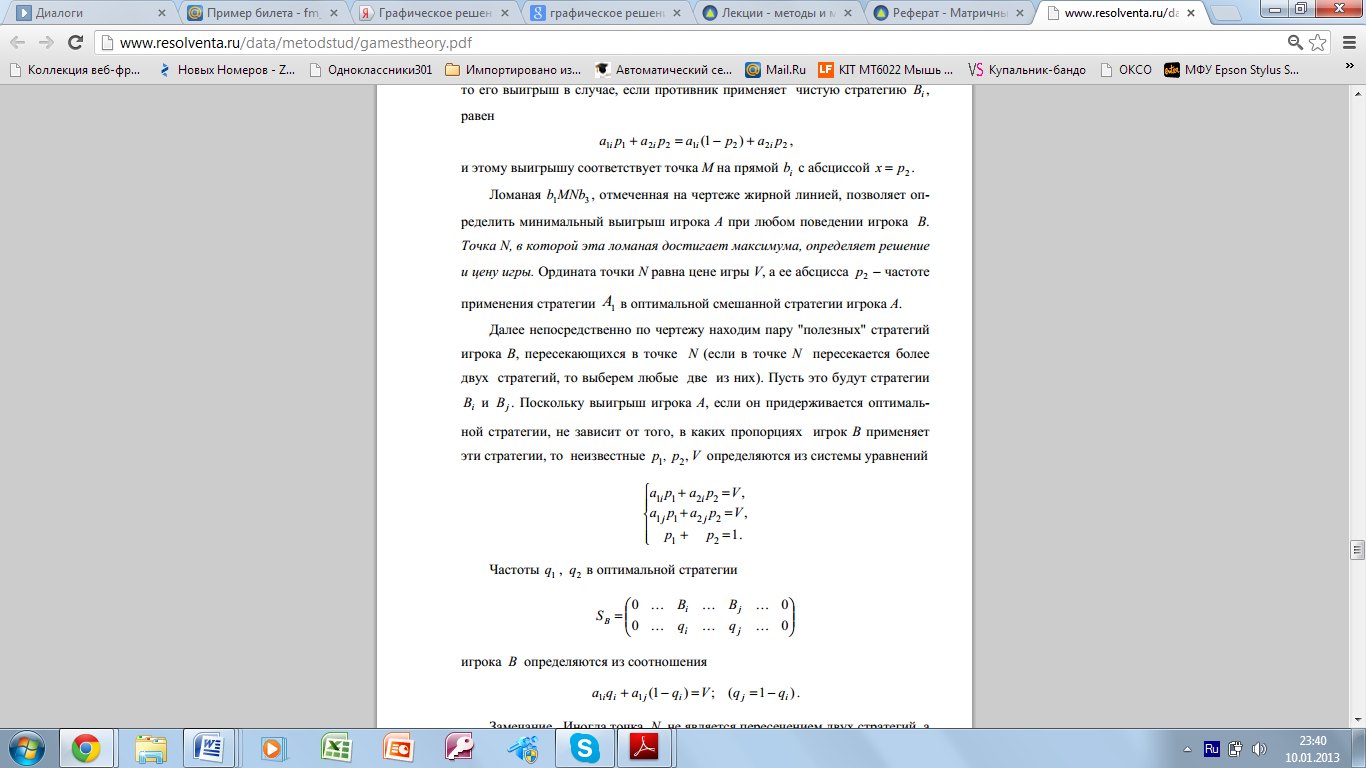 Для игры m*2 решение находится совершенно аналогично. Действительно, поскольку выигрыш игрока А одновременно является проигрышем игрока В, то для решения задачи нужно построить ломаную, соответствующую верхней границе выигрыша игрока А, а затем найти на ней точку с минимальной ординатой.
Для игры m*2 решение находится совершенно аналогично. Действительно, поскольку выигрыш игрока А одновременно является проигрышем игрока В, то для решения задачи нужно построить ломаную, соответствующую верхней границе выигрыша игрока А, а затем найти на ней точку с минимальной ординатой.
24. Метод динамического программирования. Принцип оптимальности и уравнение Беллмана.
Метод динамического программирования состоит в том что оптимальное управление строится постепенно. На каждом шаге оптимизируется управление только этого шага. Вместе с тем на каждом шаге управление выбирается с учётом последствий, так как управление, оптимизирующее целевую функцию только для данного шага, может привести к неоптимальному эффекту всего процесса. Управление на каждом шаге должно быть оптимальным с точки зрения процесса в целом. Это основное правило динамического программирования, сформулированное Беллманом, называется принципом оптимальности.
Так, если система в начале k - шага находится в состоянии 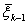 и мы выбираем произвольное управление
и мы выбираем произвольное управление 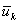 , то она придет в новое состояние в
, то она придет в новое состояние в 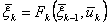 , и последующие управления
, и последующие управления 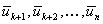 должны выбираться оптимальными относительно состояния
должны выбираться оптимальными относительно состояния 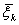 . Последнее, означает, что этих управлениях максимизируется величина
. Последнее, означает, что этих управлениях максимизируется величина 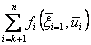 , то есть показатель эффективности на последующих до конца процесса шагах
, то есть показатель эффективности на последующих до конца процесса шагах 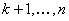 . Обозначим через
. Обозначим через 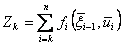 .
.
Выбрав оптимальное управление 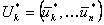 на оставшихся
на оставшихся 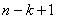 шагах, получим величину
шагах, получим величину 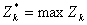 , которая зависит только от
, которая зависит только от 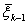 , то есть
, то есть 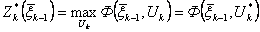 .
.
Назовем величину 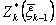 условным максимумом. Если мы теперь выберем на k-м шаге некоторое произвольное управление
условным максимумом. Если мы теперь выберем на k-м шаге некоторое произвольное управление 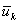 , то система придет в состояние
, то система придет в состояние 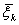 . Согласно принципу оптимальности, необходимо выбирать управление
. Согласно принципу оптимальности, необходимо выбирать управление 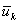 так, чтобы оно в совокупности с оптимальным управлением на последующих шагах (начиная с (k +1)-го) приводило бы к общему показателю эффективности на
так, чтобы оно в совокупности с оптимальным управлением на последующих шагах (начиная с (k +1)-го) приводило бы к общему показателю эффективности на 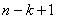 шагах, начиная с k-uго и до конца. Это положение в аналитической форме можно записать в виде следующего соотношения:
шагах, начиная с k-uго и до конца. Это положение в аналитической форме можно записать в виде следующего соотношения:
|
|
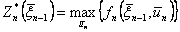 ,
,
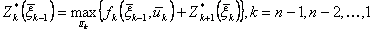 , (1)
, (1)
получившего название основного функционального уравнения динамического программирования, илиосновного рекуррентного уравнения Беллмана.
Из уравнения (1) может быть получена функция 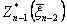 , если известно функция
, если известно функция 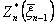 . Аналогично можно получить
. Аналогично можно получить 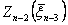 , если известно
, если известно 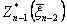 и т. д., пока не будет определена величина
и т. д., пока не будет определена величина 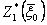 , представляющая по определению максимальное значение показателя эффективности процесса в целом:
, представляющая по определению максимальное значение показателя эффективности процесса в целом:
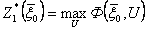 .
.
Решая уравнение (1) для определения условного максимума показателя эффективности за 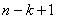 шагов, начиная с k-го, мы определяем соответствующее оптимальное управление
шагов, начиная с k-го, мы определяем соответствующее оптимальное управление 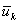 , при котором этот максимум достигается. Это управление также зависит от
, при котором этот максимум достигается. Это управление также зависит от 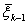 ; будем обозначать его через
; будем обозначать его через 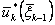 и называть условным оптимальным управлением на k-м шаге. Основное значение уравнения (1), в котором реализована идея динамического программирования, заключается в том, что решение исходной задачи определения максимума функции
и называть условным оптимальным управлением на k-м шаге. Основное значение уравнения (1), в котором реализована идея динамического программирования, заключается в том, что решение исходной задачи определения максимума функции 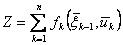 n переменных
n переменных 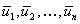 сводится к решению последовательности nзадач, задаваемых соотношениями (1), каждое из которых является задачей максимизации функции одной переменной
сводится к решению последовательности nзадач, задаваемых соотношениями (1), каждое из которых является задачей максимизации функции одной переменной 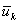 .
.
В результате последовательного решения п частных задач на условный максимум определяют две последовательности функций: 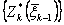 - условные максимумы и соответствующие им
- условные максимумы и соответствующие им 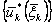 - условные оптимальные управления. Указанные последовательности функций в дискретных задачах получают в табличной форме, а в непрерывных моделях - аналитически. После выполнения первого этапа (условнойоптимизациии) приступают ко второму этапу - безусловной оптимизации.
- условные оптимальные управления. Указанные последовательности функций в дискретных задачах получают в табличной форме, а в непрерывных моделях - аналитически. После выполнения первого этапа (условнойоптимизациии) приступают ко второму этапу - безусловной оптимизации.
Если начальное состояние 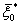 задано
задано 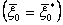 , то непосредственно
, то непосредственно
определяют максимум целевой функции
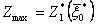 ,
,
а затем - искомое безусловное оптимальное управление по цепочке
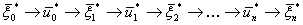 . (2)
. (2)
Если задано множество 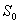 начальных состояний
начальных состояний 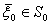 , то дополнительно решают еще одну задачу на максимум
, то дополнительно решают еще одну задачу на максимум
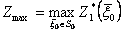 ,
,
откуда находят 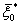 , а затем по цепочке (2) - безусловное оптимальное управление.
, а затем по цепочке (2) - безусловное оптимальное управление.
В рассмотренных рекуррентных соотношениях предписывают начинать вычисления с последнего этапа и затем передвигаться назад до этапа 1. Такой метод вычислений известен как алгоритм обратной прогонки. Если расчеты осуществляются в естественном порядке следования этапов, то такой метод вычислений известен как алгоритм прямой прогонки.
|
|
Приведем рекуррентные соотношения для этого случая. Уравнения состояний для прямого хода удобно записывать в виде
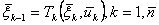 .
.
Введем в рассмотрение условные максимумы показателя эффективности за k шагов, от 1-го до k -говключительно, - величину 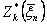 . Повторив приведенные рассуждения, придем к следующей системе уравнений Беллмана:
. Повторив приведенные рассуждения, придем к следующей системе уравнений Беллмана:
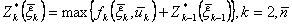 ;
;
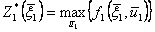 .
.
В результате решения этих уравнений получим последовательности
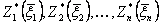 ;
; 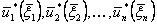 .
.
Далее определим безусловное оптимальное управление по цепочке
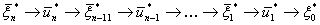 .
.
|
|
|

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!