Алгоритм Метод крутых восхождений.
Рассмотрим применение одой из разновидностей градиентных методов для решения задачи двухпараметрической задачи безусловной оптимизации. Этот метод получил название метода крутых восхождений (спусков). Пусть необходимо найти безусловный максимум функции:
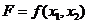 (21)
(21)
Алгоритм метода выглядит следующим образом:
1. Определить интервалы варьирования переменных x1, x2 на каждом шаге расчета. В общем случае интервалы должны быть разными Δx1 и Δx2. Если в задаче определены граничные условия вида:
 (22)
(22)
Можно принять:
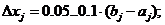 (23)
(23)
Если диапазоны изменения переменных близки, можно принять одну величину интервала варьирования для обеих.
2. Выбрать внутри ОДР начальную точку М0 с координатами 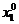 ,
,  . Вокруг точки М0 расположить 4 точки согласно рис.12. и определить их координаты:
. Вокруг точки М0 расположить 4 точки согласно рис.12. и определить их координаты:
точка 1 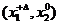 :
: 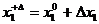 ;
;
точка 2 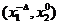 :
: 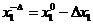 ;
;
точка 3  :
: 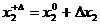 ; (24)
; (24)
точка 4  :
:  ;
;
В указанных точках определить значение ЦФ (вычислить, провести эксперименты и т.д.): 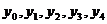 .
.

Рис.12. Расположение расчетных точек для вычисления градиента.
3. Численным способом определить компоненты вектора-градиента в точке М0. Для этого нам необходимо рассчитать значения частных производных (11). В классическом определении производная равна отношению бесконечно малого приращения функции (дифференциала) к бесконечно малому приращению переменной. При численном определении производных бесконечно малые приращения заменяются на конечные разности (рис.13):
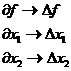 (25)
(25)
И формулы для определения частных производных будут выглядеть следующим образом:
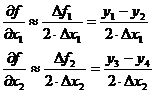 (26)
(26)

Рис.13. Определение частной производной через конечные разности.
4. Далее по формуле (12) необходимо определить направление шага (откладывается от оси х1!!!). Величину шага можно принять равной:
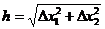 (27)
(27)
Таким образом координаты следующего положения центральной точки М0 можно определить по формулам:
 (28)
(28)
В случае, если решается задача поиска минимума ЦФ, нужно двигаться по направлению вектора-антиградиента. Т.е. в обратную сторону:
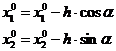 (29)
(29)
В дальнейшем шаги 2-4 следует повторять до тех пор пока не будет найдено оптимальное решение. При этом в качестве критерия окончания расчета можно принять величину градиента 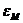 :
:  (30)
(30)
Где e – малое число (например 0.001).
Расчет по методу крутого восхождения удобно свести в таблицу.
Использование симплекс-метода при решении задач условной оптимизации.
Алгоритмы условной оптимизации симплекс-методом базируются на методах безусловной оптимизации. Т.е. задача начинает решаться так, как если бы отсутствовали ОГР и ГРУ. Однако на каждом шаге дополнительно проверяется условие нарушения границ ОДР. Если границы ОДР нарушены производится корректировка значения соответствующего параметра (см. рис.8.). В программе для расчета на ЭВМ должен присутствовать условный оператор. Этот способ хорошо работает при наличии «простых» ограничений (ГРУ). В случае если в матмодели задачи присутствуют сложные ОГР, в т.ч. нелинейные данный способ становится неэффективным. Наиболее часто для учета сложных ограничений используют методы штрафных и барьерных функций.
Суть этих методов схожа. В выражение для ЦФ вводится добавка, зависящая по величине от того, нарушены ОГР или нет. Виды модифицированных ЦФ при использовании методов барьерных и штрафных функций показаны на рис.9 и 10.
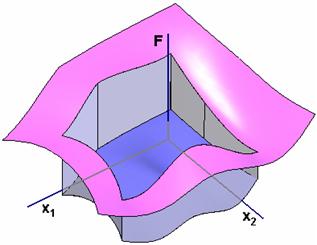
Рис.9. Вид модифицированной целевой функции при использовании метода барьерных функций.

Рис.10. Вид модифицированной целевой функции при использовании метода штрафных функций.
При использовании метода барьерных функций значение добавки внутри ОДР равно нулю, при выходе за границу ОДР она имеет «бесконечное» значение (с учетом ограничений ЭВМ). При решении задачи минимизации ЦФ имеет вид колодца с вертикальными стенками (рис.9.). При использовании метода штрафных функций величина добавки на границе ОДР равна нулю. При выходе вершины симплекса за границу расчетной области она быстро возрастает пропорционально некоторой большой величине M и суммарной величине нарушения (невязок) ограничений. ЦФ при этом также имеет вид колодца с крутыми стенками, но не вертикальными. При выходе за границу ОДР симплекс быстро «скатывается» назад в «колодец», при этом форма симплекса не нарушается. Таким образом использование МБФ и МШФ сводит задачу условной оптимизации к решению задачи безусловной оптимизации.
Рассмотрим матмодель задачи условной оптимизации:
 (5)
(5)
Модифицированная целевая функция будет иметь вид:
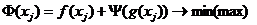 (6)
(6)
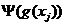 - добавка, зависящая от величины нарушения (невязки) ограничения.
- добавка, зависящая от величины нарушения (невязки) ограничения.
При использовании метода барьерных функций:

 (7)
(7)
При использовании метода штрафных функций:
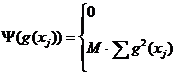 (8)
(8)
М – большое число.
Наибольшее распространение получил МШФ, т.к. он позволяет более точно решать задачи, если оптимум лежит на границе ОДР.
17.Градиентный метод решения нелинейных задач оптимизации, понятия градиента функции:
Понятие градиента функции.
Ранее было сказано, что градиентными называют пошаговые методы первого порядка. При этом величина и направление каждого шага оптимизационного расчета зависит от величины первой производной ЦФ. Направление каждого шага совпадает с градиентом ЦФ (отсюда и название методов).
Градиентом скалярной функции n переменных f(x1,x2,..,xj,..xn) называют вектор  , компонентами которого являются частные производные функции f по соответствующим направлениям:
, компонентами которого являются частные производные функции f по соответствующим направлениям:
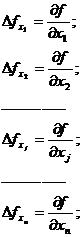 (9)
(9)
По-другому можно записать:
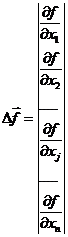 (10)
(10)
Вектор-градиент обладает тем замечательным свойством, что он показывает направление наискорейшего изменения функции. Например, если рассмотреть функцию двух переменных:
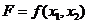
Градиент которой в точке М(х1М,х2М) равен:
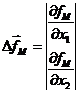 (11)
(11)
то можно сказать, что при движении в направлении 1 (рис.11), соответствующем направлению вектора-градиента в точке М функция будет возрастать в наибольшей степени по сравнению с любыми другими возможными направлениями (например, 2 или 3).

Рис.11. Вектор-градиент.
Вектор, противоположный вектору-градиенту называют антиградиентом. Он показывает направление наискорейшего убывания функции.
Учитывая это свойство вектора-градиента и строят стратегию поиска оптимального решения при использовании градиентных методов. На данном шаге вычисляют не значение функции, а значение частных производных и определяют направление градиента. Вычисленное направление градиента принимают за направление следующего шага. Например, в случае решения двухпараметрической задачи градиентным методом направление шагов может определяться углом α относительно оси Х1 (рис.11). Величина угла рассчитывается следующим образом:
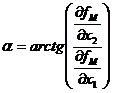 (12)
(12)
Численной мерой градиента, как и любого вектора является норма или модуль, которые равны:
 (13)
(13)
Обычно модуль градиента обозначают через 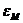 и выражение записывают более коротко:
и выражение записывают более коротко:
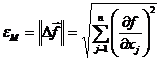 (14)
(14)
Особое внимание следует обратить на градиент линейной функции:
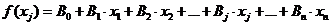 (15)
(15)
Согласно формуле (10):
 (16)
(16)
Т.к.
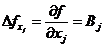 (17)
(17)
согласно формуле (9).
Видно, что для линейной функции направление и величина градиента будут постоянными.
Так, например, для линейной функции двух переменных:
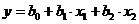 (18)
(18)
 (19)
(19)
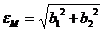 (20)
(20)
Градиентные методы позволяют найти решение задачи оптимизации за минимальное число шагов. Однако у них имеются и недостатки. Главный – необходимость вычисления на каждом шаге частных производных ЦФ. ЦФ не всегда бывает задана явно в аналитической форме (в виде формулы). Поэтому наиболее часто используют численные методы нахождения градиента. Это требует большего количества вычислений по сравнению с методами поиска. Точность при этом также может снижаться.



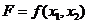 (21)
(21) (22)
(22)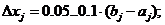 (23)
(23)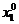 ,
,  . Вокруг точки М0 расположить 4 точки согласно рис.12. и определить их координаты:
. Вокруг точки М0 расположить 4 точки согласно рис.12. и определить их координаты: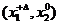 :
: 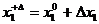 ;
; 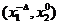 :
: 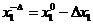 ;
;  :
: 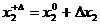 ; (24)
; (24) :
:  ;
; 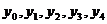 .
.
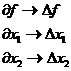 (25)
(25)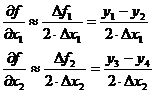 (26)
(26)
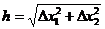 (27)
(27) (28)
(28)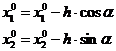 (29)
(29)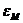 :
:  (30)
(30)

 (5)
(5)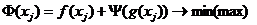 (6)
(6)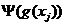 - добавка, зависящая от величины нарушения (невязки) ограничения.
- добавка, зависящая от величины нарушения (невязки) ограничения.
 (7)
(7)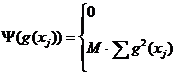 (8)
(8) , компонентами которого являются частные производные функции f по соответствующим направлениям:
, компонентами которого являются частные производные функции f по соответствующим направлениям: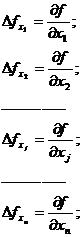 (9)
(9)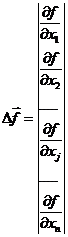 (10)
(10)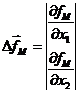 (11)
(11)
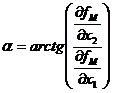 (12)
(12) (13)
(13)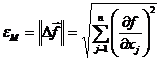 (14)
(14)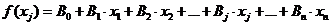 (15)
(15) (16)
(16)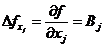 (17)
(17)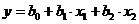 (18)
(18) (19)
(19)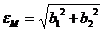 (20)
(20)


