Итак, покажем, наконец, что из существования прямой Эйлера следует существование прямых Нагеля, и наоборот.
Основная теорема
В любом треугольнике существует прямая Эйлера  в любом треугольнике существуют прямые Нагеля.
в любом треугольнике существуют прямые Нагеля.
Этот факт следует из следующих пяти утверждений:
Утверждение 7.1
В произвольном остроугольном треугольнике существует прямая Эйлера  в любом треугольнике существует прямая Нагеля.
в любом треугольнике существует прямая Нагеля.
Утверждение 7.2
В произвольном тупоугольном треугольнике существует прямая Эйлера  в любом треугольнике существуют добавочные прямые Нагеля.
в любом треугольнике существуют добавочные прямые Нагеля.
Утверждение 7.3 (обратное к утверждению 7.1)
В любом треугольнике существует прямая Нагеля  в произвольном остроугольном треугольнике существует прямая Эйлера.
в произвольном остроугольном треугольнике существует прямая Эйлера.
Утверждение 7.4 (обратное к утверждению 7.2)
В любом треугольнике существуют добавочные прямые Нагеля 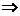 в произвольном тупоугольном треугольнике существует прямая Эйлера.
в произвольном тупоугольном треугольнике существует прямая Эйлера.
Утверждение 7.5
Существование прямой Эйлера для прямоугольного треугольника вытекает как из утверждения 7.3, так и из утверждения 7.4, являясь предельным случаем их обоих.
Последнее утверждение очевидно. Докажем остальные.
Доказательство утверждения 7.1
Пусть АВС – произвольный треугольник, а 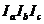 - его вневписанный треугольник. Согласно утверждению 3.4.1., вневписанный треугольник всегда остроугольный, и его углы связаны с углами исходного треугольника следующим образом:
- его вневписанный треугольник. Согласно утверждению 3.4.1., вневписанный треугольник всегда остроугольный, и его углы связаны с углами исходного треугольника следующим образом:
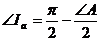 ,
, 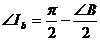 ,
, 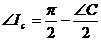 .
.
Рассмотрим аффинное преобразование 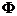 , отображающее треугольник
, отображающее треугольник 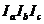 на треугольник АВС
на треугольник АВС 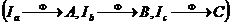 . Это преобразование переводит прямые в прямые, и сохраняет барицентрические координаты точки (см. свойство 3.2.4).
. Это преобразование переводит прямые в прямые, и сохраняет барицентрические координаты точки (см. свойство 3.2.4).
Пусть 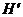 и
и 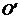 - соответственно ортоцентр и центр описанной окружности треугольника
- соответственно ортоцентр и центр описанной окружности треугольника 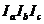 , а N и I – точка Нагеля и центр вписанной окружности треугольника АВС.
, а N и I – точка Нагеля и центр вписанной окружности треугольника АВС.
Тогда (см. 3.1.1) 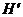
 и
и 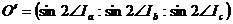 .
.
Но
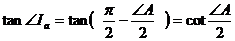 ,
,
 ,
,
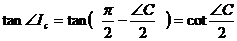 .
.
А также,
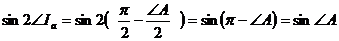 ,
,  ,
,
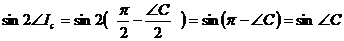
Однако, как известно (см.3.1.1),
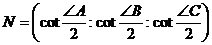 и
и  .
.
Таким образом, 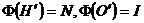 - и мы показали, что прямая Эйлера остроугольного треугольника
- и мы показали, что прямая Эйлера остроугольного треугольника 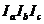 аффинным преобразованием
аффинным преобразованием 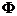 переводится в прямую Нагеля исходного треугольника АВС.
переводится в прямую Нагеля исходного треугольника АВС.
□
Доказательство утверждения 7.2
Пусть АВС – некоторый тупоугольный треугольник с тупым углом при вершине А, а 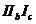 - его первый добавочный вневписанный треугольник. Согласно утверждению 3.4.2., добавочный вневписанный треугольник всегда тупоугольный, и его углы связаны с углами исходного треугольника следующим образом:
- его первый добавочный вневписанный треугольник. Согласно утверждению 3.4.2., добавочный вневписанный треугольник всегда тупоугольный, и его углы связаны с углами исходного треугольника следующим образом:
. 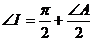 ,
, 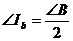 ,
, 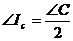
Рассмотрим аффинное преобразование 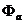 , отображающее треугольник
, отображающее треугольник 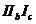 на треугольник АВС
на треугольник АВС  . Это преобразование переводит прямые в прямые, и сохраняет барицентрические координаты точки (см. свойство 3.2.4).
. Это преобразование переводит прямые в прямые, и сохраняет барицентрические координаты точки (см. свойство 3.2.4).
Пусть 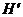 и
и 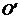 - соответственно ортоцентр и центр описанной окружности треугольника
- соответственно ортоцентр и центр описанной окружности треугольника 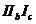 , а
, а 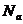 и
и 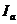 – первая добавочная точка Нагеля и центр соответствующей вневписанной окружности треугольника АВС.
– первая добавочная точка Нагеля и центр соответствующей вневписанной окружности треугольника АВС.
Тогда (см. 3.1.1) 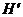
 и
и 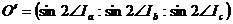 .
.
Но
 ,
, 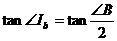 ,
,  .
.
.
А также,
 ,
, 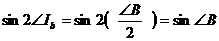 ,
,
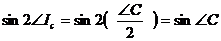 .
.
Однако, как известно (см. 3.1.1),
 и
и 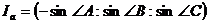 .
.
Таким образом,  - и мы показали, что прямая Эйлера тупоугольного треугольника
- и мы показали, что прямая Эйлера тупоугольного треугольника 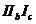 аффинным преобразованием
аффинным преобразованием 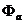 переводится в добавочную прямую Нагеля исходного треугольника АВС.
переводится в добавочную прямую Нагеля исходного треугольника АВС.
□
Доказательство утверждения 7.3
Пусть АВС – некоторый треугольник, а 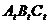 - его тангенциальный треугольник. Согласно утверждению 3.6.1., его углы связаны с углами исходного остроугольного треугольника следующим образом:
- его тангенциальный треугольник. Согласно утверждению 3.6.1., его углы связаны с углами исходного остроугольного треугольника следующим образом:
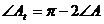 ,
, 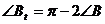 ,
, 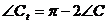 .
.
Рассмотрим аффинное преобразование 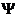 , отображающее треугольник
, отображающее треугольник 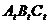 на треугольник АВС
на треугольник АВС  . Это преобразование переводит прямые в прямые, и сохраняет барицентрические координаты точки (см. свойство 3.2.4).
. Это преобразование переводит прямые в прямые, и сохраняет барицентрические координаты точки (см. свойство 3.2.4).
Пусть 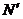 и
и 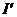 - соответственно точка Нагеля и центр вписанной окружности треугольника
- соответственно точка Нагеля и центр вписанной окружности треугольника 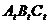 , а Н и О – ортоцентр и центр описанной окружности треугольника АВС.
, а Н и О – ортоцентр и центр описанной окружности треугольника АВС.
Тогда (см. 3.1.1.) 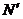
 и
и 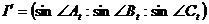 .
.
Но
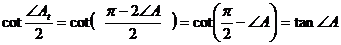 ,
,
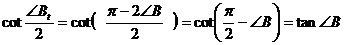 ,
,
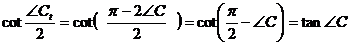 .
.
А также,
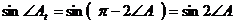 ,
,
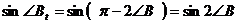 ,
,
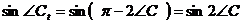 .
.
Однако, как известно (см. 3.1.1),
 и
и 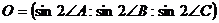 .
.
Таким образом, 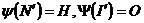 - и мы показали, что прямая Нагеля треугольника
- и мы показали, что прямая Нагеля треугольника 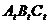 аффинным преобразованием
аффинным преобразованием 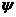 переводится в прямую Эйлера исходного остроугольного треугольника АВС.
переводится в прямую Эйлера исходного остроугольного треугольника АВС.
□
Доказательство утверждения 7.4
Пусть АВС – некоторый тупоугольный треугольник с тупым углом при вершине А, и 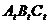 - его тангенциальный треугольник. Согласно утверждению 3.6.2., его углы связаны с углами исходного остроугольного треугольника следующим образом:
- его тангенциальный треугольник. Согласно утверждению 3.6.2., его углы связаны с углами исходного остроугольного треугольника следующим образом:
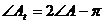 ,
,  ,
, 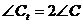 .
.
Рассмотрим аффинное преобразование  , отображающее треугольник
, отображающее треугольник 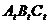 на треугольник АВС
на треугольник АВС 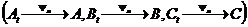 . Это преобразование переводит прямые в прямые, и сохраняет барицентрические координаты точки (см. свойство 3.2.4).
. Это преобразование переводит прямые в прямые, и сохраняет барицентрические координаты точки (см. свойство 3.2.4).
Пусть 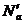 и
и  - первая добавочная точка Нагеля и центр соответствующей вневписанной окружности треугольника
- первая добавочная точка Нагеля и центр соответствующей вневписанной окружности треугольника 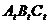 , а Н и О – ортоцентр и центр описанной окружности треугольника АВС.
, а Н и О – ортоцентр и центр описанной окружности треугольника АВС.
Тогда (см. 3.1.1) 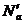
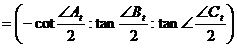 и
и 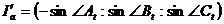 .
.
Но
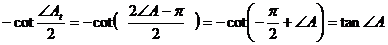 ,
,
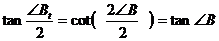 ,
,
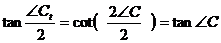 .
.
А также,
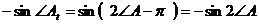 ,
,
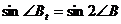 ,
,
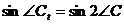 .
.
Однако, как известно (см. 3.1.1),
 и
и 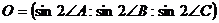 .
.
Таким образом,  - и мы показали, что добавочная прямая Нагеля треугольника
- и мы показали, что добавочная прямая Нагеля треугольника 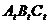 аффинным преобразованием
аффинным преобразованием 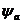 переводится в прямую Эйлера исходного тупоугольного треугольника АВС.
переводится в прямую Эйлера исходного тупоугольного треугольника АВС.
□
Приложение: Кристиан Генрих фон Нагель (1803 – 1882)
(Christian Heinrich von Nagel)
Мы говорили о прямых, названных в честь двух математиков.
Великий Эйлер оставил после себя многотомное собрание сочинений, его творчеству и жизни посвящены разнообразные исследования – при желании их несложно найти и с ними ознакомиться. А вот о Нагеле известно совсем немногое. Краткие биографические сведения удалось почерпнуть на сайте Кимберлинга (см.[3]).
Нижеследующий фрагмент заимствован именно оттуда:
| В1821 К. Г. фон Нагель приступил к изучению теологии в Тибингене. В 1825 он удостоен сана священника. Затем в течение четырех лет посещает лекции по математике и физике, которые читают в Университете Тибенгена Боненбергер (J. G. von Bohnenberger) и Рик (F. J. P. Riecke).В декабре 1826 г. Он принят учителем математики и физики (natural science) в Лицей и Реальное Училище (Realschule) Тибенгена и продолжает изучать математику в Университете. В 1830 получает докторскую степень (Ph.D.) (диссертация называлась «De triangulis rectangulis ex algebraica aequatione construendis» (название латинское – можно приблизительно понять, что речь идет о прямоугольных треугольниках и неких алгебраических соотношениях, с ними связанных), а научным руководителем был Боненбергер), и звание приват-доцента.
| 
|
Начиная с 19830 занимает должность профессора математики в Гимназии города Ульма. В 1840 заканчивает 400-страничную книгу, озаглавленную «Die Idee der Realschule, nach ihrer theoretischen Begrundung und praktischen Ausfь hrung dargestellt» (что можно перевести с немецкого примерно так: «Реальные Училища -теоретическое обоснование и практическое воплощение»). В 1844 Нагель становится ректором Реального Училища в Ульме и после 25 лет безупречной службы удостаивается титула «почетный гражданин Ульма». В 1875 выходит в отставку.
Шесть работ Нагеля имеются в книге Peter Baptist, Die Entwicklung der Neueren Dreiecksgeometrie, Wissenschaftsverlag, Mannheim, 1992. (П.Баптист, Развитие современной геометрии треугольника). В одной из этих работ Нагель приводит доказательство существования точек, которые ныне принято называть точками Нагеля и Жергонна. Однако прямую Нагеля сам Нагель, скорее всего, не открывал – во всяком случае, в дошедших до нас его работах она не упоминается. Как бы оно там ни было, прямая названа в честь Нагеля вполне заслуженно – ибо вклад этого ученого в элементарную геометрию весьма существенен.
Список литературы.
[1] Мякишев А. Элементы геометрии треугольника. М.: МЦНМО, 2002.
[2] Прасолов В. Задачи по планиметрии. М.: МЦНМО, 2007.
[3] Kimberling C. Biographical Studies.
[http://faculty.evansville.edu/ck6/bstud/index.html]
[4] Sigur S. Triangle Geometry
http://www.paideiaschool.org/Teacherpages/Steve_Sigur/geometryIndex.htm
[1] Вообще-то в случае равностороннего треугольника все три точки совпадают. Но мы и здесь, и в дальнейшем (в подобных ситуациях) будем считать случай правильного треугольника – предельным и не будем выделять его особо.
[2] Увы, этот замечательный педагог и математик скончался 5 июля 2008 года в возрасте 62 лет. Фигура в американском образовании такого же масштаба, как, например, А.Н. Земляков в российском.
[3] Вспоминается фраза из одной старой детской книжки: «Ежели кит со слоном схлестнутся, то кто кого сборет?» (Не ручаюсь за дословною точность, цитируя по памяти. А книжка, кажется, Льва Кассиля «Швамбрания»).
[4] Особенно последнее из них. Что уж говорить, подобные «аргументы» (а ты кто такой!?) - в природе человека.
[5] Автор статьи на самом деле с глубоким уважением относится ко всем гуманитарным дисциплинам и ко многим их отдельным представителям.



 в любом треугольнике существуют прямые Нагеля.
в любом треугольнике существуют прямые Нагеля. в любом треугольнике существует прямая Нагеля.
в любом треугольнике существует прямая Нагеля.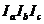 - его вневписанный треугольник. Согласно утверждению 3.4.1., вневписанный треугольник всегда остроугольный, и его углы связаны с углами исходного треугольника следующим образом:
- его вневписанный треугольник. Согласно утверждению 3.4.1., вневписанный треугольник всегда остроугольный, и его углы связаны с углами исходного треугольника следующим образом: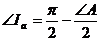 ,
, 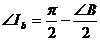 ,
, 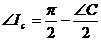 .
. , отображающее треугольник
, отображающее треугольник 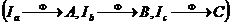 . Это преобразование переводит прямые в прямые, и сохраняет барицентрические координаты точки (см. свойство 3.2.4).
. Это преобразование переводит прямые в прямые, и сохраняет барицентрические координаты точки (см. свойство 3.2.4).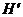 и
и 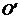 - соответственно ортоцентр и центр описанной окружности треугольника
- соответственно ортоцентр и центр описанной окружности треугольника  и
и 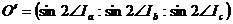 .
.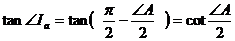 ,
, ,
,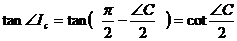 .
.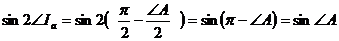 ,
,  ,
,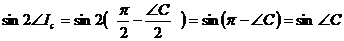
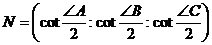 и
и  .
.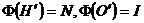 - и мы показали, что прямая Эйлера остроугольного треугольника
- и мы показали, что прямая Эйлера остроугольного треугольника 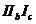 - его первый добавочный вневписанный треугольник. Согласно утверждению 3.4.2., добавочный вневписанный треугольник всегда тупоугольный, и его углы связаны с углами исходного треугольника следующим образом:
- его первый добавочный вневписанный треугольник. Согласно утверждению 3.4.2., добавочный вневписанный треугольник всегда тупоугольный, и его углы связаны с углами исходного треугольника следующим образом: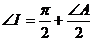 ,
, 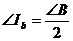 ,
, 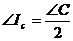
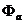 , отображающее треугольник
, отображающее треугольник  . Это преобразование переводит прямые в прямые, и сохраняет барицентрические координаты точки (см. свойство 3.2.4).
. Это преобразование переводит прямые в прямые, и сохраняет барицентрические координаты точки (см. свойство 3.2.4).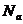 и
и 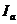 – первая добавочная точка Нагеля и центр соответствующей вневписанной окружности треугольника АВС.
– первая добавочная точка Нагеля и центр соответствующей вневписанной окружности треугольника АВС. ,
, 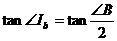 ,
,  .
. ,
, 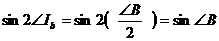 ,
,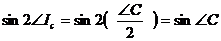 .
. и
и 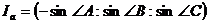 .
. - и мы показали, что прямая Эйлера тупоугольного треугольника
- и мы показали, что прямая Эйлера тупоугольного треугольника 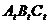 - его тангенциальный треугольник. Согласно утверждению 3.6.1., его углы связаны с углами исходного остроугольного треугольника следующим образом:
- его тангенциальный треугольник. Согласно утверждению 3.6.1., его углы связаны с углами исходного остроугольного треугольника следующим образом: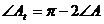 ,
, 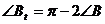 ,
, 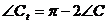 .
.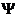 , отображающее треугольник
, отображающее треугольник  . Это преобразование переводит прямые в прямые, и сохраняет барицентрические координаты точки (см. свойство 3.2.4).
. Это преобразование переводит прямые в прямые, и сохраняет барицентрические координаты точки (см. свойство 3.2.4).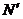 и
и 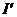 - соответственно точка Нагеля и центр вписанной окружности треугольника
- соответственно точка Нагеля и центр вписанной окружности треугольника  и
и 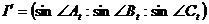 .
.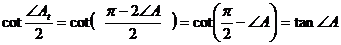 ,
,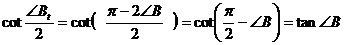 ,
,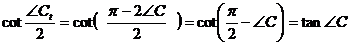 .
.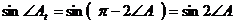 ,
,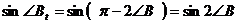 ,
,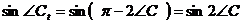 .
. и
и 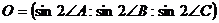 .
.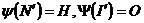 - и мы показали, что прямая Нагеля треугольника
- и мы показали, что прямая Нагеля треугольника 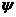 переводится в прямую Эйлера исходного остроугольного треугольника АВС.
переводится в прямую Эйлера исходного остроугольного треугольника АВС.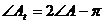 ,
,  ,
, 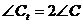 .
. , отображающее треугольник
, отображающее треугольник 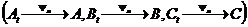 . Это преобразование переводит прямые в прямые, и сохраняет барицентрические координаты точки (см. свойство 3.2.4).
. Это преобразование переводит прямые в прямые, и сохраняет барицентрические координаты точки (см. свойство 3.2.4).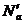 и
и  - первая добавочная точка Нагеля и центр соответствующей вневписанной окружности треугольника
- первая добавочная точка Нагеля и центр соответствующей вневписанной окружности треугольника 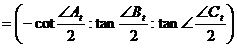 и
и 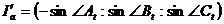 .
.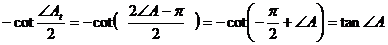 ,
,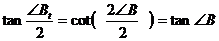 ,
,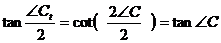 .
.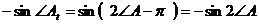 ,
,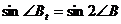 ,
,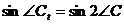 .
. - и мы показали, что добавочная прямая Нагеля треугольника
- и мы показали, что добавочная прямая Нагеля треугольника 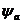 переводится в прямую Эйлера исходного тупоугольного треугольника АВС.
переводится в прямую Эйлера исходного тупоугольного треугольника АВС.



