Алгоритмы методов уточнения корней.

1) Метод градиентного спуска

 

 

2) Метод Ньютона-Рафсона

 

Пусть необходимо найти решение системы:

 

 

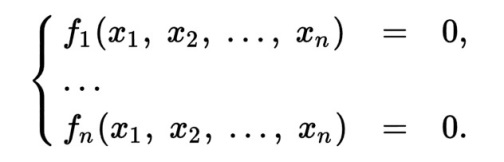
Выбирая некоторое начальное значение, последовательные приближения находят путём решения систем уравнений:

где

 

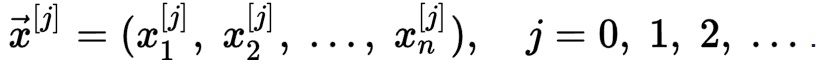
Поверхность, соответствующая функционалу системы

Решения системы уравнений тремя методами для трех точностей

eps	Метод Ньютона-Рафсона	Метод градиентного спуска	Функция sqp
1e-2	-0.28982 1.14290	-0.28518 1.13463	-0.28981 1.14288
1e-3	-0.28981 1.14288	-0.31013 1.15186	-0.28981 1.14288
1e-5	-0.28981 1.14288	-0.31448 1.15365	-0.28981 1.14288

Анализ результатов решения системы и выводы по работе.

       Запрограммированные методы Ньютона-Рафсона и градиентного спуска дают корректный результат.

       В ходе выполнения лабораторной работы я глубже ознакомился с возможностями системы математических вычислений GNUOctave, получил дополнительный опыт программирования на языке, который используется в данной системе, а также изучил и проанализировал методы решения систем нелинейных уравнений.

 

Текст программы

disp("Start\n");

function y=F(x)

y = (sin(x(1))+2*x(2)-2).^2+(cos(x(2)-1)+x(1)-0.7).^2;

endfunction

 

 

y=x=[-5:0.1:5];

[xx,yy] = meshgrid(x,y);

z = (sin(xx)+2*yy-2).^2+(cos(yy-1)+xx-0.7).^2;

mesh(x,y,z);

 

disp("Using SQP function");

X = [0,0];

[x, obj, info, iter] = sqp (X, @F)

 

disp("Gradient descent");

grad_x = inline('2*(cos(x)*sin(x)+2*y-2)+x+cos(1-y)-0.7');

grad_y = inline('4*(sin(x)+2*y-2)+2*sin(1-y)*(x+cos(1-y)-0.7)');

X = [0;0];

EPS = 1e-5;

n = 0;

grad = [];

h = 0.182;

 

do

tmp = X;

grad(1,:) = grad_x(X(1),X(2));

grad(2,:) = grad_y(X(1),X(2));

X = X - h*grad;

n++;

until (abs(F(X)-F(tmp))<=EPS);

X

n

 

disp("Newton-Raphson's method");

w1 = inline('sin(x)+2*y-2');

w2 = inline('cos(y-1)+x-0.7');

J1 = inline('cos(x)');

J2 = 2;

J3 = 1;

J4 = inline('sin(1-y)');

n = 0;

X = [0;0];

 

do

w = [ w1(X(1),X(2)); w2(X(1),X(2))];

Jacobian = [ J1(X(1)), J2; J3, J4(X(2)) ];

delta = inv(Jacobian)*w;

X = X - delta;

n++;

until (abs(delta) <= EPS)

X

n

 

 

Задание и исходные данные к лабораторной работе.

F1(x,y) = cos(x-1)+y=0.5

F2(x,y) = x-cos(y)=3

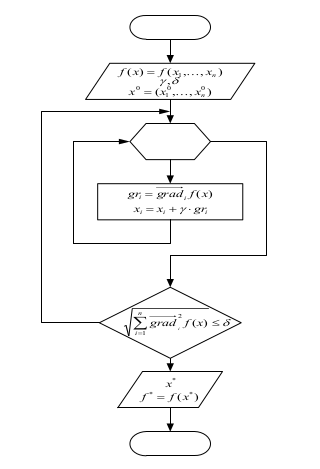
Метод наискорейшего спуска

Алгоритм

На каждом шаге метод «приближается» к решению последовательно покаждой из координат. Переход от точки х к к точке х к+1 назовем внешнейитерацией. Внутри каждой «внешней» итерации находятся n внутреннихдля последовательного вычисления координат точки х к+1

 

 

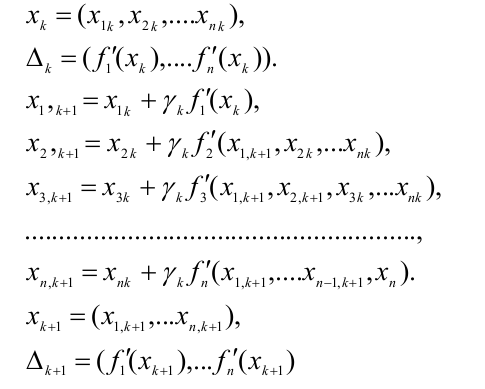
1. Поверхностьфункционаласистемы:

 

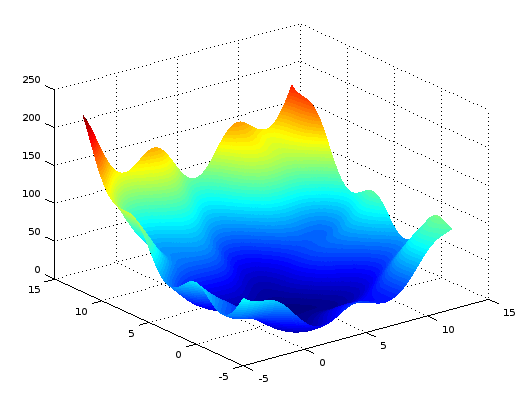
2. ОпределимВизуальноминимумфункционала:

x = 4;

y = 1.5;

 

3. Графикилинийуровняфункционала:

 

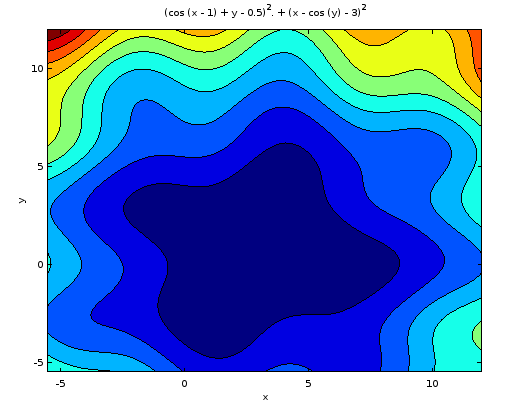
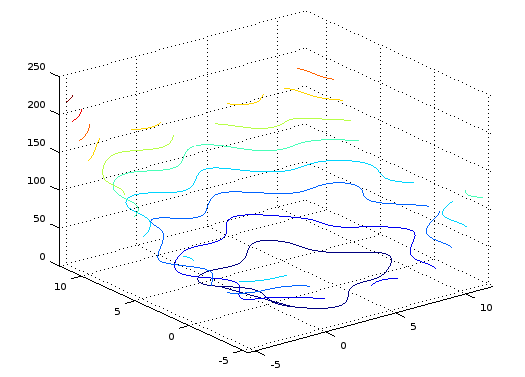
4. Результатырешенияразнымиметодами:

Уточнение корней:

eps	Метод Ньютона -Рафсона	Наискорейший спуск	Функция spq
1E-2	x1 = 3.3559 y1 = 1.2069	ans = 4   3.3562 1.2070	x = 3.3559 1.2069   obj = 1.4379e-16 info = 101 iter = 7
1E-3	x1 = 3.3559 y1 = 1.2069	ans = 5   3.3559 1.2069	x = 3.3559 1.2069   obj = 1.7616e-16 info = 101 iter = 9
1E-5	x1 = 3.3559 y1 = 1.2069	ans = 8   3.3559 1.2069	x = 3.3559 1.2069   obj = 1.7423e-16 info = 101 iter = 13

x⁽⁰⁾ = [4; 1.5](Наискорейший спуск и метод Ньютона-Рафсона)

начальный шаг равен 0.3.(Наискорейший спуск)

 

 

Тексты программ

%главнаяпрограмма

y=x=[-5.5:0.01:12];

[xx, yy] = meshgrid (x, y);

z=(cos(xx-1)+yy-0.5).^2.+(xx-cos(yy)-3).^2;

%mesh(x,y,z)

%x0 = [4,1.5];

%[x,obj,info,iter] = sqp(x0,@phi)

 

fq = @(x,y) (cos(x-1)+y-0.5).^2.+(x-cos(y)-3).^2;

%ezcontourf (fq, [-5.5, 12],200);

 

 

%contour3(x,y,z)

 

%функционал

function y = phi(x)

                              y = (cos(x(1)-1)+x(2)-0.5).^2+(x(1)-cos(x(2))-3).^2;

endfunction;

 

%методЗейделя-Гаусса

functionXm = GaussSeidelMin(phi, x0, d, g)

% минимизацияпокоординатнымспуском (методГаусса-Зейделя)

% Xm - координтаыминимума

% phi - функциядвухпеременных, котойищетсяминиммум

% x0 - координатыначальнойточки

% d - точность

% g - постояннаяшага

k = 1; %Счетчикшагов

kmax =500; % Предельноечислошагов,

% задаетсядляпредотвращениязацикливания

% Массивыдляхраненияпромежуточныхкоординат

x1 = x0(1);

x2 = x0(2);

x1trace = [x1];

x2trace = [x2];

i = 2;

h = 1e-5; % приращениедлярассчетаградиентов

whilek<kmax

% Спускпопервойкоординате

gr1 = (phi(x1+h,x2)-phi(x1-h,x2))/(2*h); % производнаяпох1

x1 = x1 - g*gr1;

% Сохранениекоординат

x1trace(i) = x1;

x2trace(i) = x2;

i = i + 1;

% Спускповторойкоординате

gr2 = (phi(x1,x2+h)-phi(x1,x2-h))/(2*h); % производнаяпох2

x2 = x2 - g*gr2;

% Сохранениекоординат

x1trace(i) = x1;

x2trace(i) = x2;

i = i + 1;

% Проверкаусловияостанова

ifsqrt(gr1^2 + gr2^2) <= d;

break; % Выходизциклавслучаевыполненияусловия

end

k = k + 1;

end

Xm = [x1, x2]; % координатыминимума

ifk>= kmax

disp('Минимумненайден!')

disp('Изменитезначениешага')

end

k

endfunction;

function newton = Func(x)

                              newton = [0; 0];

                              newton(1) = cos(x(1)-1)+x(2)-0.5;

                              newton(2) = x(1)-cos(x(2))-3;

endfunction;

GaussSeidelMin(fq, [4,1.5], 1e-2, 0.3);

cur_x = [10; 10];

Eps = 1e-5;

delta = 0;

count = 0;

do

                              count++;

                              W = [-sin(-1+cur_x(1)), 4; 1.5, sin(cur_x(2))];

                              B = (-1)*Func(cur_x);

                              delta = inv(W)*B;

                              cur_x += delta;

until (max(abs(delta)) <Eps || count > 1000);

 

disp('МетодНьютона-Рафсона')

x

y

count