Системе координат
Всякое комплексное число  удобно изображать точкой
удобно изображать точкой  на комплексной плоскости
на комплексной плоскости 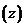 (рис. 1). Оси
(рис. 1). Оси 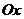 и
и 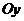 прямоугольной декартовой системы координат на этой плоскости называются соответственно действительной и мнимой осями. Между точками плоскости
прямоугольной декартовой системы координат на этой плоскости называются соответственно действительной и мнимой осями. Между точками плоскости  и изображенными на ней комплексными числами существует взаимно однозначное соответствие.
и изображенными на ней комплексными числами существует взаимно однозначное соответствие.
Одновременно с этим каждая точка  плоскости определяет вектор
плоскости определяет вектор 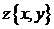 с началом в начале системы координат и концом в этой точке, проекции которого на оси координат будут соответственно х и y. Длина (модуль) этого вектора
с началом в начале системы координат и концом в этой точке, проекции которого на оси координат будут соответственно х и y. Длина (модуль) этого вектора
 . (2.8)
. (2.8)
Действительные числа 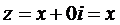 изображаются на комплексной плоскости точками (х, о) оси
изображаются на комплексной плоскости точками (х, о) оси 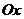 или векторами, параллельными этой оси, а число
или векторами, параллельными этой оси, а число 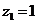 будет являться единичным вектором оси
будет являться единичным вектором оси 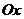 .
.
Действительные числа 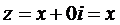 изображаются на комплексной плоскости точками (х, 0) оси
изображаются на комплексной плоскости точками (х, 0) оси 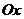 или векторами, параллельными этой оси, а число
или векторами, параллельными этой оси, а число 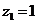 будет являться единичным вектором оси
будет являться единичным вектором оси 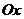 .
.
Чисто мнимым числам 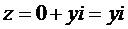 будут соответствовать точки
будут соответствовать точки  оси
оси 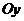 или векторы, параллельные этой оси. Число
или векторы, параллельные этой оси. Число  изображается точкой (0, 1) мнимой оси и одновременно являться единичным вектором
изображается точкой (0, 1) мнимой оси и одновременно являться единичным вектором 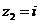 оси
оси 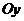 . Любая пара комплексно-сопряженных чисел z и
. Любая пара комплексно-сопряженных чисел z и  на комплексной плоскости изображается векторами
на комплексной плоскости изображается векторами 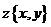 и
и  , симметричными действительной оси
, симметричными действительной оси 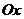 (рис. 1).
(рис. 1).
Векторы 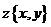 являются свободными векторами, поэтому их начало можно совмещать с любой точкой комплексной плоскости путем параллельного переноса. Сложение и вычитание комплексных чисел можно рассматривать как сложение и вычитание соответствующих векторов, совмещая их начало с точкой О (рис. 2).
являются свободными векторами, поэтому их начало можно совмещать с любой точкой комплексной плоскости путем параллельного переноса. Сложение и вычитание комплексных чисел можно рассматривать как сложение и вычитание соответствующих векторов, совмещая их начало с точкой О (рис. 2).
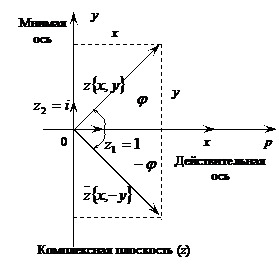
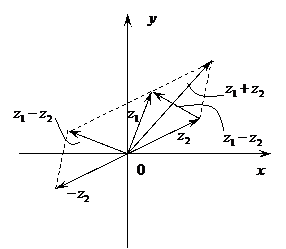
Рис. 1 Рис. 2
С помощью комплексных чисел можно задавать различные множества точек комплексной плоскости 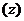 , что используется при анализе различных функций комплексной переменной и графическом изображении области их определения.
, что используется при анализе различных функций комплексной переменной и графическом изображении области их определения.
Полярная система координат. Тригонометрическая формула
Комплексного числа
Совместим начало координат системы xOy с полюсом т. О и ось Ох с полярной осью p (рис.1) Введем в рассмотрение длину | z | вектора z { x, y } и угол φ, образованный вектором z с положительным направлением оси Ох. Этот угол называется аргументом комплексного числа и обозначается 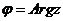 . Угол
. Угол 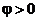 , если отсчет его производится против направления движения часовой стрелки, и
, если отсчет его производится против направления движения часовой стрелки, и 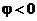 , если по часовой стрелке. Очевидно, что для всякого комплексного числа
, если по часовой стрелке. Очевидно, что для всякого комплексного числа 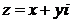 справедливы формулы:
справедливы формулы:
 ;
; 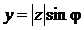 ;
;
 ;
; 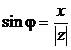 ;
; 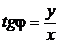 ; (2.9)
; (2.9)
где 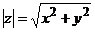 ,
,  .
.
При этом необходимо учитывать, что для любого комплексного числа его аргумент А rgz при 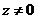 может иметь бесконечное множество значений, отличающихся одно от другого на слагаемое кратное
может иметь бесконечное множество значений, отличающихся одно от другого на слагаемое кратное 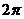 . Поэтому условия равенства комплексных чисел заключается в том, что длины (модули) должны быть равны, а аргументы φ могут отличаться на величины, кратные
. Поэтому условия равенства комплексных чисел заключается в том, что длины (модули) должны быть равны, а аргументы φ могут отличаться на величины, кратные 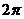 .
.
Из множества значений Argz для практических расчетов выделяют одно, лежащее в интервале  ,которое обозначают а rgz. Оно называется главным значением аргумента комплексного числа:
,которое обозначают а rgz. Оно называется главным значением аргумента комплексного числа:
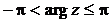 или
или  . (2.10)
. (2.10)
Очевидно 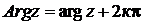 , где
, где 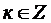 . (2.11)
. (2.11)
Для нахождения главного аргумента комплексного числа удобно использовать следующие формулы:

для точек z первой и второй четверти
комплексной плоскости,
для точек второй четверти, (2.12)
для точек третьей четверти.
Числа 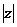 и углы
и углы  является полярными координатами точки z, т.е.
является полярными координатами точки z, т.е. 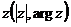 .
.
Используя алгебраическую форму 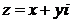 и формулы (2.9) получим тригонометрическую форму комплексного числа
и формулы (2.9) получим тригонометрическую форму комплексного числа
 . (2.13)
. (2.13)
В тригонометрическом виде комплексно-сопряженное число  , т.к.
, т.к. 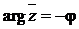 , выражается формулой
, выражается формулой
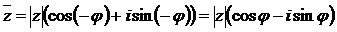 (2.14)
(2.14)
Пример. Изобразить комплексные числа 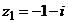 и
и 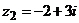 на комплексной плоскости и записать их в тригонометрической форме.
на комплексной плоскости и записать их в тригонометрической форме.
Решение. Оба числа представлены в алгебраической форме. Изобразим эти числа на комплексной плоскости и определим сначала модули 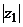 и
и 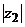 и главные аргументы
и главные аргументы  и
и 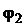 (рис. 3).
(рис. 3).
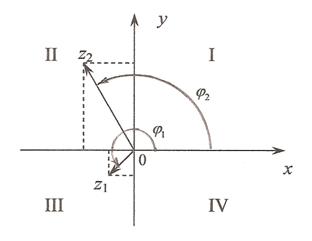
Рис. 3
1. 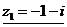
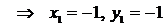 ,
,  .
.
Число 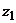 или его вектор
или его вектор  находятся в III четверти. Используя формулу (2.12) для этой четверти, имеем
находятся в III четверти. Используя формулу (2.12) для этой четверти, имеем
 , или
, или 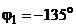 .
.
Если воспользоваться положительным значением угла 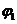 , показанным на рис. 3, тогда
, показанным на рис. 3, тогда 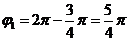 или
или 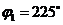 . Тригонометрическая форма числа
. Тригонометрическая форма числа 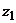 принимает вид:
принимает вид:
 или
или 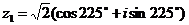 .
.
Подставив в последние формулы значения 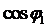 и
и 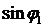 , придем к исходной алгебраической форме этого числа
, придем к исходной алгебраической форме этого числа 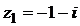 .
.
2.  ,
, 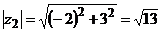 .
.
Число 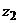 и его вектор
и его вектор 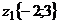 находятся во II четверти. На основании формулы (2.12) получим
находятся во II четверти. На основании формулы (2.12) получим
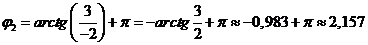 рад, или
рад, или 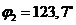 ;
;
 или
или 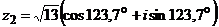 .
.



 удобно изображать точкой
удобно изображать точкой  на комплексной плоскости
на комплексной плоскости 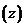 (рис. 1). Оси
(рис. 1). Оси 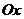 и
и 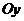 прямоугольной декартовой системы координат на этой плоскости называются соответственно действительной и мнимой осями. Между точками плоскости
прямоугольной декартовой системы координат на этой плоскости называются соответственно действительной и мнимой осями. Между точками плоскости  и изображенными на ней комплексными числами существует взаимно однозначное соответствие.
и изображенными на ней комплексными числами существует взаимно однозначное соответствие.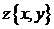 с началом в начале системы координат и концом в этой точке, проекции которого на оси координат будут соответственно х и y. Длина (модуль) этого вектора
с началом в начале системы координат и концом в этой точке, проекции которого на оси координат будут соответственно х и y. Длина (модуль) этого вектора . (2.8)
. (2.8)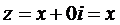 изображаются на комплексной плоскости точками (х, о) оси
изображаются на комплексной плоскости точками (х, о) оси 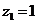 будет являться единичным вектором оси
будет являться единичным вектором оси 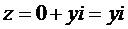 будут соответствовать точки
будут соответствовать точки  оси
оси  изображается точкой (0, 1) мнимой оси и одновременно являться единичным вектором
изображается точкой (0, 1) мнимой оси и одновременно являться единичным вектором 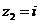 оси
оси  на комплексной плоскости изображается векторами
на комплексной плоскости изображается векторами 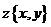 и
и  , симметричными действительной оси
, симметричными действительной оси 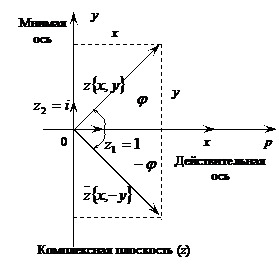

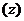 , что используется при анализе различных функций комплексной переменной и графическом изображении области их определения.
, что используется при анализе различных функций комплексной переменной и графическом изображении области их определения.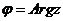 . Угол
. Угол 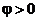 , если отсчет его производится против направления движения часовой стрелки, и
, если отсчет его производится против направления движения часовой стрелки, и 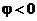 , если по часовой стрелке. Очевидно, что для всякого комплексного числа
, если по часовой стрелке. Очевидно, что для всякого комплексного числа 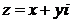 справедливы формулы:
справедливы формулы: ;
; 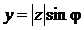 ;
; ;
; 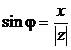 ;
; 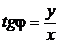 ; (2.9)
; (2.9)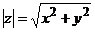 ,
,  .
.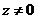 может иметь бесконечное множество значений, отличающихся одно от другого на слагаемое кратное
может иметь бесконечное множество значений, отличающихся одно от другого на слагаемое кратное 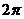 . Поэтому условия равенства комплексных чисел заключается в том, что длины (модули) должны быть равны, а аргументы φ могут отличаться на величины, кратные
. Поэтому условия равенства комплексных чисел заключается в том, что длины (модули) должны быть равны, а аргументы φ могут отличаться на величины, кратные  ,которое обозначают а rgz. Оно называется главным значением аргумента комплексного числа:
,которое обозначают а rgz. Оно называется главным значением аргумента комплексного числа: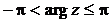 или
или  . (2.10)
. (2.10)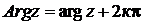 , где
, где 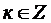 . (2.11)
. (2.11)
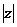 и углы
и углы  является полярными координатами точки z, т.е.
является полярными координатами точки z, т.е. 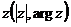 .
. . (2.13)
. (2.13) , т.к.
, т.к. 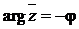 , выражается формулой
, выражается формулой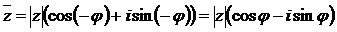 (2.14)
(2.14)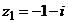 и
и 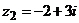 на комплексной плоскости и записать их в тригонометрической форме.
на комплексной плоскости и записать их в тригонометрической форме.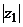 и
и 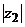 и главные аргументы
и главные аргументы  и
и 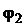 (рис. 3).
(рис. 3).
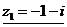
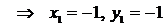 ,
,  .
.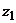 или его вектор
или его вектор  находятся в III четверти. Используя формулу (2.12) для этой четверти, имеем
находятся в III четверти. Используя формулу (2.12) для этой четверти, имеем , или
, или 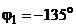 .
.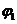 , показанным на рис. 3, тогда
, показанным на рис. 3, тогда 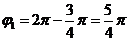 или
или 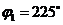 . Тригонометрическая форма числа
. Тригонометрическая форма числа  или
или 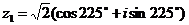 .
.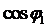 и
и 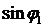 , придем к исходной алгебраической форме этого числа
, придем к исходной алгебраической форме этого числа 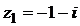 .
. ,
, 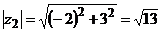 .
.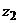 и его вектор
и его вектор 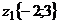 находятся во II четверти. На основании формулы (2.12) получим
находятся во II четверти. На основании формулы (2.12) получим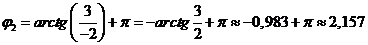 рад, или
рад, или 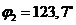 ;
; или
или 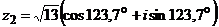 .
.


