

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы...
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Интересное:
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
В предыдущем разделе показано, что в частном случае постоянных цен исходную задачу (4) можно записать в форме двухэтапной задачи стохастического линейного программирования с квантильным критерием. Исследуем полученную задачу (12).
Рассмотрим задачу второго этапа (19). Заметим, что из ограничений (15), (16), (18) при неотрицательности параметров  ,
,  ,
,  , следует ограниченность множества допустимых стратегий в задаче (19). При тех же значениях параметров
, следует ограниченность множества допустимых стратегий в задаче (19). При тех же значениях параметров  ,
,  ,
,  и неотрицательном
и неотрицательном  нулевой вектор переменных
нулевой вектор переменных  удовлетворяет ограничениям задачи (19), поэтому множество допустимых стратегий в задаче (19) непусто. Значит, при указанных ограничениях на параметры решение задачи (19) существует при любой допустимой стратегии первого этапа и любой реализации вектора случайного спроса.
удовлетворяет ограничениям задачи (19), поэтому множество допустимых стратегий в задаче (19) непусто. Значит, при указанных ограничениях на параметры решение задачи (19) существует при любой допустимой стратегии первого этапа и любой реализации вектора случайного спроса.
Из теории двойственности задач линейного программирования известно, что в случае существования решения задачи линейного программирования (19) оптимальные значения критериев задачи (19) и двойственной к ней совпадают. Таким образом,

где  — вектор двойственных переменных,
— вектор двойственных переменных,  — множество допустимых значений двойственных переменных.
— множество допустимых значений двойственных переменных.
Задача (22) при фиксированных  ,
,  является задачей линейного программирования, решение которой существует. Значит, максимум критериальной функции задачи (22) достигается в одной из вершин множества
является задачей линейного программирования, решение которой существует. Значит, максимум критериальной функции задачи (22) достигается в одной из вершин множества  .
.
Найдём множество 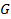 , состоящее из всех вершин множества
, состоящее из всех вершин множества  . Рассмотрим матрицу
. Рассмотрим матрицу  . Пусть
. Пусть  — базисная подматрица (невырожденная квадратная подматрица размерности
— базисная подматрица (невырожденная квадратная подматрица размерности  матрицы
матрицы  ).
).  — подматрица матрицы
— подматрица матрицы  , составленная из строк
, составленная из строк  , которые не вошли в соответствующую базисную подматрицу
, которые не вошли в соответствующую базисную подматрицу  .
.
Рассмотрим вектор  . Пусть
. Пусть 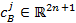 — подвектор вектора
— подвектор вектора  , составленный из тех элементов
, составленный из тех элементов  , номера которых совпадают с номерами строк матрицы
, номера которых совпадают с номерами строк матрицы  , вошедшими в матрицу
, вошедшими в матрицу  . Пусть
. Пусть  — соответствующий подвектор вектора
— соответствующий подвектор вектора  , составленный из элементов
, составленный из элементов  , которые не вошли в
, которые не вошли в  .
.
|
|
Тогда множество 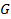 представимо в виде
представимо в виде
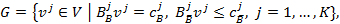 (23)
(23)
где  — число базисных подматриц матрицы
— число базисных подматриц матрицы  .
.
Таким образом, для нахождения всех вершин множества  необходимо перебрать
необходимо перебрать  , где
, где  — биномиальный коэффициент, невырожденных квадратных подматриц матрицы
— биномиальный коэффициент, невырожденных квадратных подматриц матрицы  , последовательно решая системы
, последовательно решая системы

Пусть множество  состоит из
состоит из  точек. Тогда функцию оптимального значения критерия задачи второго этапа
точек. Тогда функцию оптимального значения критерия задачи второго этапа  можно записать в виде
можно записать в виде

Подставим полученную функцию  в задачу (12):
в задачу (12):

где  ,
,

Таким образом, двухэтапная задача (12) сводится к одноэтапной задаче (26) стохастического линейного программирования с квантильным критерием [11], в которой целевая функция потерь имеет вид (27).
В [12] доказана следующая теорема.
Теорема 1[12]. Если  ,
,  и множество
и множество  состоит только из нулевого вектора, то решение задачи (26) существует и
состоит только из нулевого вектора, то решение задачи (26) существует и  .
.
Заметим, что теорема сформулирована в отсутствие каких-либо предположений о виде закона распределения вектора случайных параметров  .
.
Справедливо следствие из теоремы 1.
Следствие. Если  ,
,  ,
,  ,
,  ,
,  и выполнено условие
и выполнено условие

то решение задачи (12) существует и  .
.
Доказательство. Выше была доказана эквивалентность задач (26) и (12) при выполнении условий  ,
,  ,
,  ,
,  . Значит, решения данных задач либо совпадают, либо не существуют. В силу структуры матрицы
. Значит, решения данных задач либо совпадают, либо не существуют. В силу структуры матрицы 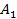 множество
множество  состоит только из нулевого вектора. Кроме того, при выполнении условий (28) гарантируется непустота множества допустимых стратегий первого этапа. Таким образом, все условия теоремы 1 выполнены. Следствие доказано. ■
состоит только из нулевого вектора. Кроме того, при выполнении условий (28) гарантируется непустота множества допустимых стратегий первого этапа. Таким образом, все условия теоремы 1 выполнены. Следствие доказано. ■
С экономической точки зрения ограничение (28) означает, что максимальный объём инвестирования превосходит суммарный объём инвестирования, необходимый для поддержания производства на прежнем уровне.
|
|
|

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!