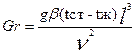ТЕМА №1
Техническая термодинамика.
1.Основные понятия и определения.
Термодинамика изучает законы превращения энергии в различных процессах, происходящих в макроскопических системах, и сопровождается тепловыми эффектами (макроскопическая система- это объект, который состоит из большого числа частиц). Техническая термодинамика изучает закономерности взаимного превращения тепловой и механической энергии и свойства тел, участвующих при этом вращении.
Вместе с теорией теплообмена она является теоретическим фундаментом теплотехники.
Термодинамическая система представляет собой совокупность материальных тел, находящихся в механическом и тепловом взаимодействии друг с другом и с окружающим систему внешними телами (внешней средой).
Сведения по физике
Основные параметры: температура, давление и удельный объем.
Под температурой понимают физическую величину, характеризующую степень нагретости тела. Применяют 2 температурные шкалы: термодинамическую Т(°К) и международную практическую t (°С). Соотношение между Т и t определяется по значениям тройной точки воды:
Т= t(°С)+273,15
Тройная точка воды – состояние, при котором твердое, жидкое и газообразное фазы находятся в равновесии.
За единицу давления принимается Паскаль (Па) данная единица очень мала, поэтому используют большие величины кПа, МПа. А также внесистемные единицы измерения – техническая атмосфера и миллиметры ртутного столба. (мм.рт.ст.)
Рн =760мм.рт.ст.=101325 Па=101,325 кПа = 0,1 МПА=1кг/см
Основные параметры состояния газа связаны между собой уравнением:

Уравнение Клайперона 1834г.
R- Удельная газовая постоянная.
Умножив левую и правую части на m, получим уравнение Менделеева, Клайперона, где m- молекулярная масса вещества:
m×R×u=R×T×m
Значение произведения m× R называют универсальной газовой постоянной, её выражение определяется из формулы:
m×R= 
При нормальных физических условиях:  Дж/(Кмоль*К).
Дж/(Кмоль*К).
Где  m×Vн=22,4136
m×Vн=22,4136  /Кмоль - молярный объем идеального газа при нормальных физических условиях.
/Кмоль - молярный объем идеального газа при нормальных физических условиях.
Удельная газовая постоянная R- это работа, затраченная на нагревание 1 кг вещества на 1 К при постоянном давлении
R=  ,
,
Если все термодинамические параметры постоянны во времени и одинаковы во всех точках системы, то такое состояние системы называется равновесным. Если между различными точками в системе существуют разности температур, давлений и других параметров, то она является неравновесной. В такой системе под действием градиентов параметров возникают потоки теплоты, вещества и другие, стремящиеся вернуть её в состояние равновесия. Опыт показывает, что изолированная система с течением времени всегда приходит в состояние равновесия и никогда самопроизвольно выйти из него не может. В классической термодинамике рассматривается только равновесные системы т.е.:
В реальных газах, в отличие от идеальных, существуют силы межмолекулярных взаимодействий (силы притяжений, когда молекулы находятся на значительном расстоянии и силы отталкивания, когда молекулы отталкиваются). И нельзя пренебречь собственным объемом молекул. Для равновесной термодинамической системы существует функциональная связь между параметрами состояния, которое называется уравнением состояния.
Опыт показывает, что удельный объем, температура и давление простейших систем, которыми являются газы, пары или жидкости связаны термическим уравнением состояния вида:
f r,u,T)=0
Уравнения состояния реальных газов.
Наличие межмолекулярных сил отталкивания приводят к тому, что молекулы могут сближаться между собой до некоторого минимального расстояния. Поэтому можно считать, что свободные для движения молекул, объем будет равен:
u-b;
где b- тот наименьший объем, до которого можно сжать газ.
В соответствии с этим длина свободного пробега уменьшается и число ударов о стенку в единицу времени, а следовательно давление увеличивается.
 ,
,  ,
,
Возникает молекулярное (внутреннее) давление.
Сила молекулярного притяжения каких-либо 2 малых частей газа пропорциональна произведению числа молекул в каждой из этих частей, т.е. квадрату плотности, поэтому молекулярное давление обратнопропорционально квадрату удельного объема газов: Рмол £ 
Где а - коэффициент пропорциональности, зависящий от природы газов.
Отсюда уравнение Ван-дер-Ваальса (1873г.)

При больших удельных объемах и сравнительно невысоких давлениях реального газа уравнение Ван-дер-Ваальса практически выражается в уравнение состояния идеального газа Клайперона. Ибо величина  (по равнению с Р) и b по сравнению с u становятся пренебрежимо малыми.
(по равнению с Р) и b по сравнению с u становятся пренебрежимо малыми.
Внутренняя энергия.
Известно, что молекулы газа в процессе хаотичного движения обладают кинетической энергией и потенциальной энергией взаимодействия, поэтому под влиянием энергии (U) понимается вся энергия, заключенная в теле или системе тел. Внутреннюю кинетическую энергию можно представить в виде кинетической энергии поступательного движения, вращательного и колебательно движения частиц. Внутренняя энергия является функцией состояния рабочего тела. Её можно представить в виде функции двух независимых переменных:
 U=f(p,v); U=f(p,T); U=f(U,T);
U=f(p,v); U=f(p,T); U=f(U,T);
В термодинамических процессах изменяемая внутренняя энергия не зависит от характера процесса. И определяется начальным и конечным состоянием тела:
DU=U2 –U1=f(p2 v2T2)-f(p1 v1 T1);
где U2- значение внутренней энергии в конце процесса;
U1 – значение внутренней энергии в начальном состоянии;
При Т=const.
Джоуль в своих исследованиях для идеального газа сделал вывод, что внутренняя энергия газ зависит только от температуры: U=f(T);
В практических расчетах определяется не абсолютное значение энергии а ее изменения:
DU=U2 – U1;
Работа газа.

Сжатие газа в цилиндре
При повышенном давлении газ, находящийся в цилиндре стремиться расширяться. На поршень действует сила G. При подводе теплоты (Q) поршень переместиться в верхнее положение на расстояние S. При этом газ совершит работу расширения. Если принять давление на поршень P, а площадь поперечного сечения поршня F, то совершаемая газом работа:
Dl=P×F×S;
Учитывая, что F×S- изменение объема, который занимает газ можно записать, что:
Dl=P×Du;
а в дифференциальной форме:  ;
;
Удельная работа расширения 1 кг газа после конечного изменения объема:
 ;
;
Изменение dl, dv всегда имеют одинаковые знаки, т.е. если dv>0, тогда имеет место работа расширения против внешних сил и она в этом случае положительная. При сжатии газа Du<0 работа совершается над газом внешними силами, поэтому она отрицательная.

Рис.- процесс расширения в диаграмме ПВ.
Заштрихованная площадь выражает величину совершаемой работы:
 ;
;  ;
;
Таким образом, механическое взаимодействие между термодинамической системой и окружающей средой зависит от двух параметров состояния- давления и объема. Работа измеряется в Джоулях. Поэтому в качестве работы тел, предназначенных для преобразования тепловой энергии в механическую, нужно выбирать такие, которые способны значительно расширять свой объем в ДВС. Газообразные продукты сгорания различных видов топлива.
Теплота
Теплота может предаваться на расстоянии (излучением) и непосредственным соприкосновением между телами. Например, теплопроводностью и конвективным теплообменом. Необходимым условием передачи теплоты является разность температур между телами. Теплота это энергия, которая передается от одного тела к другому при их непосредственном взаимодействии, которое зависит от температуры этих тел dg>0. Если dg<0, то имеет место отвод теплоты.
Первый закон термодинамики.
Первый закон термодинамики является частным случаем общего закона сохранения энергии: «Энергия не создается из ничего и не исчезает бесследно, а превращается из одной формы в другую в строго определенных количествах» (Ломоносов).
В результате подвода теплоты тело нагревается (dt>0) и увеличивается его объем, поэтому увеличение объема связано с наличием внешней работы:
 или Q=DU+ L
или Q=DU+ L
Где Q- общее количество тепла, приведенного к системе.
DU- изменение внутренней энергии.
L- работа, направленная на изменение объема термодинамической системы.
Теплота, сообщаемая термодинамической системе идет на увеличение внутренней энергии и на совершение внешней работы.
Первый закон:
«невозможно создать машину производящую работу без того чтобы эквивалентное количество энергии другого вида не исчезала» (Вечный двигатель первого рода)
То есть невозможно построить двигатель, который вырабатывал бы энергию из ничего. Иначе вырабатывал бы энергия не потребляя при этом какую-либо другую энергию.
Теплоемкость.
Для того чтобы повысить температуру любого вещества, необходимо подвести определенное количество теплоты. Выражение истинной теплоемкости:
 ,
,
Где  - элементарное количество теплоты.
- элементарное количество теплоты.
dt – соответствующие изменения температуры вещества в данном процессе.
Выражение показывает удельную теплоемкость, то есть количество теплоты необходимое подвести единице количества вещества для нагревания его на 1 К (или 1 °С). Различают массовую теплоёмкость (С) отнесенную к 1 кг. Вещества, необходимую (С’) отнесенную к 1  вещества и киломольную (mС) отнесенную к 1 кмолю.
вещества и киломольную (mС) отнесенную к 1 кмолю.
Удельная теплоемкость – это отношение теплоемкость тела к его массе:
 ;
;  - объемная.
- объемная.
Процессы с подводом теплоты при постоянном давлении называется изобарными, а с подводом теплоты при постоянном объеме – изохорным.
При теплотехнических расчетах в зависимости от процессов теплоемкости получают соответствующие названия:
Сv- изохорная теплоемкость,
Ср- изобарная теплоемкость.
Теплоемкость при изобарном процессе (p=const)
 ,
,
При изохорном процессе:
 ,
,
Уравнение Майера:
Ср-Сv=R - показывает связь между изобарным и изохорным процессами.
В процессах V=const работа не совершается а полностью расходуется на изменение внутренней энергии dq=dU, при изобарном подворье теплоты имеет месть увеличение внутренней энергии и совершение работы против внешних сил, поэтому изобарная теплоемкость Ср всегда больше изохорной на величину газовой постоянной R.
Энтальпия
В термодинамике важную роль играет сумма внутренней энергии системы U и произведения давления системы р на её объем V, называемая энтальпией и обозначается Н.
Н=U+pV,
Т.к. входящие в нее величины являются функциями состояния, то и сама энтальпия является функцией состояния, также как и внутренняя энергия, работа и теплота она измеряется в Дж.
Удельная энтальпия h=H/M представляет собой энтальпию системы, содержащей 1 кг вещества, и измеряется в Дж/кг. Изменение энтальпии в любом процессе определяется только начальным и конечным состояниями тела и не зависит от характер процесса.
Физический смысл энтальпии выясним на примере:
Рассмотрим расширенную систему, включающую газ в цилиндре и поршень с грузом, общим весом G. Энергия этой системы складывается из внутренней энергии газа и потенциальной энергии поршня с грузом.
E=U+Gy;
В условиях равновесия G=pF эту функцию можно выразить через параметры газа:
E=U+p∙FУ;

Получаем, что ЕºН, т.е. энтальпию можно трактовать как энергию расширенной системы. Если давление системы сохраняется независимым, т.е. осуществляется изобарный процесс dp=0, то qP = h2 - h1, т.е. теплота, подведенная к системе при постоянном давлении, идет только на измерение энтальпии данной системы. Это выражение очень часто используется в расчетах, так как огромное количество процессов подводов теплоты в термодинамике (в паровых котлах, камерах сгорания газовых турбин и реактивных двигателей, теплообменных аппаратах) осуществляется при постоянном давлении. При расчетах практический интерес представляет изменение энтальпии в конечном процессе:
 ;
;
Энтропия
Название энтропия происходит от греческого слова «энтропос»- что означает превращение, обозначается буквой S, измеряется [Дж/К], а удельная энтропия [Дж/кг×К]. В технической термодинамике является функцией, которая характеризует состояние рабочего тела, следовательно является функцией состояния:  ,
,
где 
 - полный дифференциал некоторой функции состояния.
- полный дифференциал некоторой функции состояния.
Формула применима для определения изменения энтропии, как идеальных газов, так и реальных может быть представлен в виде зависимости от параметров:

Это означает, что элементарное количество подведенной (отведенной) удельной теплоты в равновесных процессах равно произведению термодинамической температуры на изменение удельной энтропии.
Понятие энтропии позволяет ввести чрезвычайно удобную для термодинамических расчетов TS - диаграмму, на которой, как и на PV- диаграмме состояние термодинамической системы изображается точкой, а равновесный термодинамический процесс линией
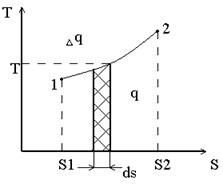
Dq - Элементарное количество теплоты.
 ;
;
Очевидно, что в TS-диаграмме элементарная теплота процесса изображается элементарной площадкой с высотой Т и основанием dS, а площадь, ограниченная линиями процесса, крайними ординатами и осью абсцисс, эквивалентна теплоте процесса.
Если Dq>0, то dS>0
Если Dq<0, то dS<0 (отвод теплоты).
Термодинамические процессы
Основные процессы:
1. Изохорный – протекает при постоянном объеме.
2. Изобарный - протекает при постоянном давлении.
3. Изотермический - протекает при постоянной температуре.
4. Адиабатный – процесс, при котором отсутствует теплообмен с окружающей средой.
5. Политропный - процесс, удовлетворяющий уравнению 

Метод исследования процессов, не зависящий от их особенностей и являющейся общим состоит в следующем:
1. Выводится уравнением процесса, устанавливающего связь между начальным и конечным параметрами рабочего тела в данном процессе.
2. Вычисляется работа изменения объема газа.
3. Определяется количество теплоты, подведенной или отведенной газу в процессе.
4. Определяется изменение внутренней энергии системы в процессе.
5. Определяется изменения энтропии системы в процессе.
а) Изохорный процесс.
Выполняется условие: dV=0 V=const.
Из уравнения состояния идеального газа следует, что P/T = R/V = const, т.е. давление газ прямопропорционально его абсолютной температуре p2/p1 = T2/T1


Работа, расширенная в этом процессе равна 0.
Количество теплоты 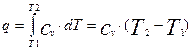 ;
;
Изменение энтропии в изохорном процессе определяется по формуле:
 ; т.е.
; т.е.
Зависимость энтропии от температуры на изохоре при Сv = const имеет логарифмический характер изменения.
б) изобарный процесс p=const
из уравнения состояния идеального газа при p=const, находим
V/T=R/p=const V2/V1=T2/T1, т.е. в изобарном процессе объем газа пропорционален его абсолютной температуре


Количество теплоты находим из формулы:
 ;
;
Изменение энтропии при Сp=const:
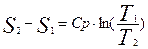 , т.е.
, т.е.
температурная зависимость энтропии при изобарном процессе тоже имеет логарифмических характер, но поскольку Ср > Сv, то изобара в TS- диаграмме идет более полого, чем в изохоре.
в) Изотермический процесс.
При изотермическом процессе: pV=RT=const p2/p1=V1/V2, т.е. давление объем обратно пропорциональны друг другу, так что при изотермическом сжатие давление газа возрастает, а при расширении падает (закон Бойля-Мариотта)

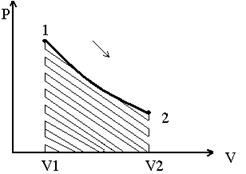
Работа процесса:  ;
;
Так как температура не меняется, то внутренняя энергия идеального газа в данном процессе остается постоянной: DU=0 и вся подводимая к газу теплота полностью превращается в работу расширения q=l.
При изотермическом сжатии от газа отводится теплота в количестве равном затраченной на сжатии работе.
Изменение энтропии: 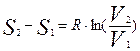 .
.
г) Адиабатный процесс.
Процесс, происходящий без теплообмена с окружающей средой, т.е. D q=0.
Чтобы осуществить процесс нужно либо теплоизолировать газ, либо провести процесс настолько быстро, чтобы изменения температуры газа, обусловленные его теплообменом с окружающей средой, было пренебрежимо мало по сравнению с изменением температуры, вызванным расширением или сжатием газа.
Уравнение адиабаты идеального газа при постоянном отношении теплоемкости:
p1 ∙ ν1k = p2 ∙ ν2k
k = CP / CV- показатель адиабаты.
k- определяется числом степеней свободы молекулы.
Для одноатомных газов к=1,66.
Для двухатомных газов к=1,4.
Для трехатомных газов к=1,33.


 ;
;
В данном процессе теплообмен газа с окружающей средой исключается, поэтому q=0, поскольку при адиабатном процессе элементарное количество теплоты D q=0, энтропия рабочего тела не изменяется dS=0; S=const.
Политропный процесс.
Любой произвольный процесс можно описать в pV- координатах (по крайней мере на небольшом участке.)
pνn = const, подбирая соответствующее значение n.
Процесс, описываемый таким уравнением называется политропным, показатель политропы n может принимать любое значение (+µ;-µ), но для данного процесса он является величиной постоянной.
Политропные процессы идеального газа.
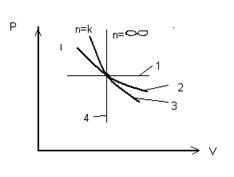
Где: 1. изобара.
2. изотерма.
3. адиабата.
4. изохора.
Теплота процесса:  ;
;
где  - массовая теплоемкость политропного процесса.
- массовая теплоемкость политропного процесса.
| Процесс
| n
| Сn
|
| Изохорный
| +µ
| Cv
|
| Изобарный
|
| Ср
|
| Изотермический
|
| µ
|
| адиабатный
| к
|
|
Изохора n=±µ делит поле диаграммы на 2 области: Процессы, находящиеся правее изохор характеризуются положительной работой, т.к. сопровождаются расширением рабочего тела; для процессов, расположенных левее изохоры характерна отрицательная работа. Процессы расположенные правее и выше адиабаты идут с подводом теплоты к рабочему телу; процессы лежащие левее и ниже адиабаты протекают с отводом теплоты.
Для процессов расположенных над изотермой (n=1) характерно увеличение внутренней энергии газа. Процессы, расположенные под изотермой сопровождаются уменьшением внутренней энергией. Процессы, расположенные между адиабатой и изотермой имеют отрицательную теплоемкость.
Водяной пар.
Пар над жидкостью, имеющей туже температуру, что и кипящая вода, но существенно больший объем называется насыщенным.
Сухой насыщенный пар - пар, не содержащий капелек жидкости и получающийся в результате законченного парообразования. Пар, содержащий влагу, называется влажным.
Влажный, насыщенный пар - смесь сухого насыщенного пара с мельчайшими капельками воды, взвешенными в его массе.
Пар, имеющий температуру более высокую, чем температура насыщения при том же давлении называется насыщенным или перегретым паром.
Степень сухости насыщенного пара (паросодержания)- это масса сухого пара в 1 кг. Влажного (Х);
 ;
;
где Мсп- масса сухого пара.
Мвп- масса влажного пара.
Для кипящей воды Х=0. Для сухого насыщенного пара Х=1.
Второй закон термодинамики
Закон определяет направление, в котором протекают процессы и устанавливаются условия преобразования тепловой энергии в механическую.
Все без исключения тепловые двигатели должны иметь горячий источник теплоты, рабочее тело, совершающее замкнутый процесс- цикл и холодный источник теплоты:

Где dS-полный дифференциал энтропии системы.
dQ- количество теплоты, полученной системой от источника тепла, при бесконечно малом процессе.
Т- абсолютная температура источника теплоты.
При бесконечно малом изменении состояния термодинамической системы, изменение энтропии системы определяется вышеназванной формулой, где знак равенства относится к обратимым процессам, знак больше к необратимым.
Истечение газа из сопла.
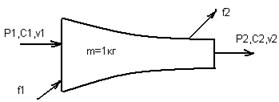
Рассмотрим сосуд в котором находится газ массой 1 кг, создаем давление Р1>Р2, учитывая что сечение на входе f1 >f2, запишем выражение для определения работы адиабатного расширения. Будем считать m (кг/с) массовый расход газа.
С- скорость истечения газа м/с.
v- удельный объем.
f- площадь сечения.
Объемный расход газа:
Mv=fc.
Считая процесс истечения газа адиабатным dq=0.
Полная работа истечения газа из сопла равна:
ln=lp+l; где
lp- работа расширения.
l- работа проталкивания.
Работа адиабатного расширения равна:
 ;
;
Где к- показатель адиабаты.
Так как l= p2v2 – p1v1
 ;
;
Полная работа расходуется на приращение кинетической энергии газа, при его движении в сопле, поэтому её можно выразить через приращение этой энергии.
 ,
,
Где с1, с2 – скорости потока на входе и выходе из сопла.
Если с2 >с1, то  ,
,
Скорости являются теоретическими, так как не учитывают потери при движении в сопле.
Действительная скорость всегда меньше теоретической.
 ,
,
j=0,93¸0,98.
Истечение паров
Получение ранее формулы полной работы справедливы лишь для идеального газа с постоянной теплоемкостью скорость истечения паров. Скорость истечения паров определяют с помощью iS- диаграмм или таблиц.
При адиабатном расширении работа пара определяется по формуле:
Ln= i1-i2
Ln - удельная работа.
i1-i2 - энтальпия пара на выходе из сопла.
Скорость и течение пара определяется:
 ,
,
С2g= С2j,
где j=0,93¸0,98; i1-i2=h – теплоперепад l=h;
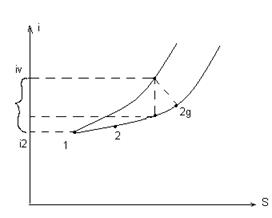
1-2g-действительный процесс расширения пара (политропный)
hg= i1-i2g - действительный теплоперепад.
В действительности процесс истечения пара из сопла не является адиабатным. Из-за трения потока пара о стенки сопла, без возвратно теряется часть его энергии. Действительный процесс протекает по линии 1-2g-поэтому действительный теплоперепад меньше теоретического в результате чего действительная скорость истечения пара несколько меньше теоретической.
Паротурбинная установка.
Простейшая паротурбинная установка.

Г- генератор.
1- паровой котел.
2- пароперегреватель.
3- паровая турбина.
4- конденсатор.
5- питательный насос.
Установки находят широкое применение в теплоэнергетике народного хозяйства. Рабочее тело- водяной пар.
Регенеративный цикл.

Практический подогрев питательной воды в схеме производится паром, отбираемым из турбины, такой подогрев называется регенеративным. Он может быть одноступенчатым, когда подогрев осуществляется паром 1-ого давления, или многоступенчатым, если подогрев производится последовательно паром различных давлений, отбираемым из различных точек (ступеней) турбины. Перегретый пар поступает из перегревателя 2 в турбину 3 после расширения в ней часть пара отбирается из турбины и направляется в первый по ходу пара подогреватель 8, остальная часть пара продолжает расширяться в турбине. Далее пар отводится во второй подогреватель 6, остающееся количество пара после дальнейшего расширения в турбине поступает в конденсатор 4. Конденсат из конденсатора насосом 5 подается во второй подогреватель, где подогревается паром, затем насосом 7 подается в первый подогреватель, после чего насосом 9 подается в котел 1.
Термический КПД регенеративного цикла увеличивается с числом отбора пара, однако увеличение количества отборов связано с усложнением и удорожанием установки, поэтому число отборов обычно не превышает 7-9. КПД цикла примерно составляет 10-12 % с увеличением числа отборов.
Теплофикационный цикл.

В паросиловых установках охлаждающая вода имеет температуру выше температуры окружающей среды. И выбрасывается в водоем, при этом теряется около 40 % подведенного тепла. Более рациональными являются установки, в которых часть тепловой энергии используется в турбогенераторах для выработки электроэнергии, а другая часть идет на нужды тепловых потребителей. Тепловые станции, работающие по такой схеме, называются Тепло Электроцентралями (ТЭЦ).
Цикл ТЭЦ: охлаждающая вода, нагретая в конденсаторе, не выбрасывается в водоем, а прогоняется через отопительные системы помещений, отдавая в них тепло и охлаждаясь одновременно. Температура горячей воды для целей отопления должна быть не менее 70-100°С. А температура пара в конденсаторе должна быть на 10-15 °С выше. Коэффициент использования тепла в теплофикационном цикле составляет 75-80%. В не теплофикационных установках около 50%. При этом повышается экономичность и КПД. Что позволяет экономить ежегодно до 15% всего расходуемого тепла.
ТЕМА №2
Основы теплопередачи.
Теплопередача - это процесс переноса теплоты от одного теплоносителя к другому через разделяющую стенку. Сложный процесс переноса теплоты разбивают на ряд наиболее простых, такой прием облегчает его изучение. Каждый простой в процессе переноса теплоты подчиняется своим законом.
Существуют 3 простейших способа передачи теплоты:
1. Теплопроводность;
2. Конвекция;
3. Излучение.
Явление теплопроводности состоит в переносе теплоты микрочастицами (молекулами, атомами, электронами и т.д.) такой теплообмен может происходить в любых телах с неоднородным распределением температур.
Конвективный теплоперенос (конвекция) наблюдается лишь в жидкостях и газах.
Конвекция -это перенос теплоты с макроскопическими обменами веществ. Конвекцией можно передавать теплоту на очень большие расстояния (при движении газа по трубам). Движущаяся среда (жидкость или газ), используются для переноса теплоты, называется теплоносителем. За счет излучения теплота передается во всех лучепрозрачных средах, в том числе и в вакууме. Носителями энергии при теплообмене излучением является фотоны, излучаемые и поглощаемые телами, участвующими в теплообмене.
ПРИМЕР: осуществление нескольких способов одновременно: Конвективная теплопередача от газа к стенке практически всегда сопровождается параллельным переносом теплоты излучения.
Основные понятия и определения.
Интенсивность переноса теплоты характеризуется плотностью теплового потока.
Плотность теплового потока - количество теплоты, передаваемое в единицу времени через единичную плотность поверхности q, Вт/м2.
Мощность теплового потока - (или тепловой поток)- количество теплоты, передаваемая в единицу времени через производную поверхность F
q=Q/F, [ 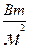 ]
]
Перенос теплоты зависит от распределения температуры во всех точках тела или системы тел в данный момент времени. Математическое описание температурного тела имеет вид:
t=f(x,y,z,  ),
),
где t- температура.
x,y,z- пространственные координаты.
 - время.
- время.
Температурное поле, описываемое приведенным уравнением, называется нестационарным. В этом случае температура зависит от времени. Если распределение температуры в теле не изменяется со временем, температурное поле называется стационарным.
t=f(x,y,z,)
Если температура изменяется только по одной или двум пространственным координатам, то температурное поле называется одно или двухмерным.
t=f(x,  )
)
Поверхность, во всех точках которой температура одинакова называется изотермической. Изотермические поверхности могут быть замкнутыми, но не могут пересекаться. Быстрее всего температура изменяется при движении в направлении перпендикулярном изотермической поверхности.
Скорость изменения температуры по нормали изотермической поверхности характеризуется градиент температуры.

Градиент температуры grad t – есть вектор, направленный по нормали к изотермической поверхности и численно равный производной от температуры по этому направлению:
 ,
,
n0 – единичный вектор, направленный в сторону возрастания температур, нормально к изотермической поверхности.
Температурный градиент является вектором положительное положение которого совпадает с увеличением температур.
Однослойная плоская стенка.

Где δ – толщина стенки.
tст1,tст2- температура поверхности стенки.
tст1>tст2
λ=const.
Тепловой поток в соответствии с законом Фурье вычисляется по формуле:

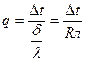 ,
,
Где Rл=δ/ λ.- внутреннее термическое сопротивление теплопроводности стенки.
Распределение температуры в плоской однородной стенке линейное. Значение λ находят в справочниках при
tср =0,5(tст1+tст2).
Тепловой поток (мощность теплового потока) определяется по формуле:
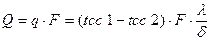 .
.
ТЕМА №3
Конвективный теплообмен.
Жидкие и газообразные теплоносители нагреваются или охлаждаются при соприкосновении с поверхностями твердых тел.
Процесс теплообмена между поверхностью твердого тела и жидкостью называется теплопередачей, а поверхность тела через которую переносится теплота поверхностью теплообмена или теплоотдающей поверхностью.
Согласно закону Ньютона – Рихмана тепловой поток в процессе теплоотдачи пропорционален площади поверхности теплообмена F и разности температур поверхности tст и жидкости tж.
 ,
,
В процессе теплоотдачи независимо от направления теплового потока Q(от стенки к жидкости или наоборот) значение его можно считать положительным, поэтому разность tст - tж берут по модулю.
Коэффициент пропорциональности α называется коэффициентом теплоотдачи, его единица измерения (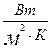 ). Он характеризует интенсивность процесса теплоотдачи. Коэффициент теплоотдачи обычно определяют экспериментально (по формуле Ньютона - Рихмана) при измеренных остальных величинах
). Он характеризует интенсивность процесса теплоотдачи. Коэффициент теплоотдачи обычно определяют экспериментально (по формуле Ньютона - Рихмана) при измеренных остальных величинах
Коэффициент пропорциональности α зависит от физических свойств жидкости и характера её движения. Различают естественное и вынужденное движение (конвекцию) жидкости. Вынужденное движение создается внешним источником (насосом, вентилятором). Естественная конвекция возникает за счет теплового расширения жидкости, нагретой около теплоотдающей поверхности в самом процессе теплообмена. Она будет тем сильнее, чем больше разность температур tст - tж и температурный коэффициент объемного расширения.
Факторы (условия):
1. Физические свойства жидкости или газов (вязкость, плотность, теплопроводность, теплоемкость)
2. Скорость движения жидкости или газа.
3. Характер движение жидкости или газа.
4. Форма омываемой поверхности.
5. Степень шероховатости поверхности.
Числа подобия
Так как коэффициент теплоотдачи зависит от многих параметров, то при экспериментальном исследовании конвективного теплообмена нужно уменьшить их число, согласно теории подобия. Для этого их объединяют в меньшее число переменных, называемых числами подобия (они безразмерны). Каждое из них имеет определенный физический смысл.
Число Нуссельта Nu=α·l/λ.
α- коэффициент теплоотдачи.
λ- коэффициент теплопроводности.
Представляет собой безразмерный коэффициент теплоотдачи, характеризует теплоотдачу на границе жидкости или газа со стенкой.
Число Рейнольдса Re=Wж·l /ν.
Где Wж- скорость движения жидкости (газа). (м/с)
ν- кинематическая вязкости жидкости.
Определяет характер потока.
Число Прандтля Pr=c·ρν/λ.
Где с - теплоемкость.
ρ – плотность жидкости или газа.
Состоит из величин, характеризующих теплофизические свойства вещества, и по существу само является теплофизической константой вещества.
Число Грасгофа 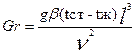
g=9,81 м/с2.
β- коэффициент объемного расширения жидкости или газа.
Характеризует отношение подъемной силы, возникающей вследствие теплового расширения жидкости, к силам вязкости.
Лучистый теплообмен.
Тепловое излучение – есть результат превращения внутренней энергии тел в энергию электромагнитных колебаний. Тепловое излучение как процесс распространения электромагнитных волн характеризуется длино





 Дж/(Кмоль*К).
Дж/(Кмоль*К). m×Vн=22,4136
m×Vн=22,4136  /Кмоль - молярный объем идеального газа при нормальных физических условиях.
/Кмоль - молярный объем идеального газа при нормальных физических условиях. ,
, ,
,  ,
,

 (по равнению с Р) и b по сравнению с u становятся пренебрежимо малыми.
(по равнению с Р) и b по сравнению с u становятся пренебрежимо малыми. U=f(p,v); U=f(p,T); U=f(U,T);
U=f(p,v); U=f(p,T); U=f(U,T);
 ;
; ;
;
 ;
;  ;
; или Q=DU+ L
или Q=DU+ L ,
, - элементарное количество теплоты.
- элементарное количество теплоты. вещества и киломольную (mС) отнесенную к 1 кмолю.
вещества и киломольную (mС) отнесенную к 1 кмолю. ;
;  - объемная.
- объемная. ,
, ,
,
 ;
; ,
, - полный дифференциал некоторой функции состояния.
- полный дифференциал некоторой функции состояния.

 ;
;


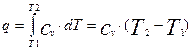 ;
; ; т.е.
; т.е.

 ;
;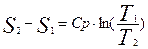 , т.е.
, т.е.

 ;
;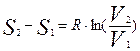 .
.

 ;
;
 ;
; - массовая теплоемкость политропного процесса.
- массовая теплоемкость политропного процесса. ;
;

 ;
; ;
; ,
, ,
, ,
, ,
,



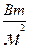 ]
] ),
),
 ,
,

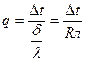 ,
,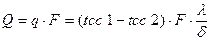 .
. ,
,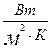 ). Он характеризует интенсивность процесса теплоотдачи. Коэффициент теплоотдачи обычно определяют экспериментально (по формуле Ньютона - Рихмана) при измеренных остальных величинах
). Он характеризует интенсивность процесса теплоотдачи. Коэффициент теплоотдачи обычно определяют экспериментально (по формуле Ньютона - Рихмана) при измеренных остальных величинах