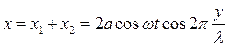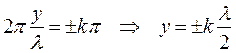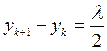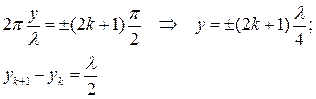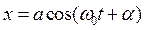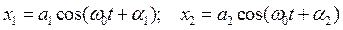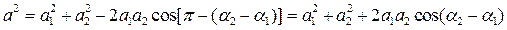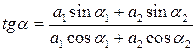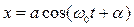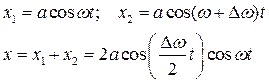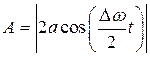Лекция №5
Механика
Колебания
Затухающие колебания. Характеристики затухающих колебаний. Вынужденные колебания. Резонанс.
Затухающие колебания
 На предыдущей лекции мы рассмотрели примеры колебаний некоторых механических колебательных систем совершающих гармонические колебания. Мы рассмотрели случаи так называемых собственных колебаний. То есть таких колебаний, которые совершаются без постоянного внешнего воздействия и которые потому называются собственными. В наших примерах колебания в рассматриваемых системах происходит с постоянной во времени амплитудой и частотой колебания. Это так называемые незатухающие колебания. Однако в реальности в любой колебательной системе присутствует трение, приводящее к потере энергии колебательного процесса, поэтому колебания в любой реальной колебательной системе затухают. Разберем пример затухающих колебаний.
На предыдущей лекции мы рассмотрели примеры колебаний некоторых механических колебательных систем совершающих гармонические колебания. Мы рассмотрели случаи так называемых собственных колебаний. То есть таких колебаний, которые совершаются без постоянного внешнего воздействия и которые потому называются собственными. В наших примерах колебания в рассматриваемых системах происходит с постоянной во времени амплитудой и частотой колебания. Это так называемые незатухающие колебания. Однако в реальности в любой колебательной системе присутствует трение, приводящее к потере энергии колебательного процесса, поэтому колебания в любой реальной колебательной системе затухают. Разберем пример затухающих колебаний.
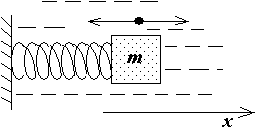
Рассмотрим колебания пружинного маятника погруженного в какую либо жидкость. (Строго говоря, даже воздушную среду можно считать некоей сплошной средой, жидкостью). Любая жидкость обладает вязкостью, которое определяет трение движущихся твердых тел. Эта сила трения при малых скоростях пропорциональна скорости тела. Таким образом, уравнение колебаний пружинного маятника с учетом сил трения будет выглядеть как: md 2 x / dt 2 = - m dx / dt - kx.
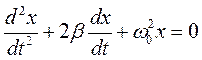 Разделим обе части уравнения на m и перенесем все члены в левую часть, после чего обозначив m / m и k / m через 2β и w 0 2 соответственно, получим дифференциальное уравнение, описывающее колебания в механической системе с вязким трением.
Разделим обе части уравнения на m и перенесем все члены в левую часть, после чего обозначив m / m и k / m через 2β и w 0 2 соответственно, получим дифференциальное уравнение, описывающее колебания в механической системе с вязким трением.
Отметим, что w 0 это та частота, с которой система бы совершала колебания в отсутствии трения. Это частота собственных колебаний системы.
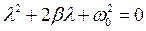 Решение полученного дифференциального уравнения будем искать в виде x ~ e l t. Подставляя это выражение в наше уравнение и произведя необходимое дифференцирование и сокращение, получим
Решение полученного дифференциального уравнения будем искать в виде x ~ e l t. Подставляя это выражение в наше уравнение и произведя необходимое дифференцирование и сокращение, получим
Это уравнение получило название характеристического уравнение. Решая это уравнение относительно l получим его значение при котором выбранный нами вид функции превращает дифференциальное уравнение в тождество. Таким образом, выбранная нами функция превращается в решение дифференциального уравнения.
Характеристическоое уравнения имеет два корня, которые равны:
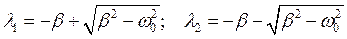
Пусть затухание будет слабым таким, чтобы β < w 0 тогда преобразуем корень и получим
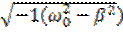 обозначим
обозначим 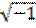 как i и
как i и 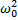 - β2 обозначим как ω2
- β2 обозначим как ω2
тогда 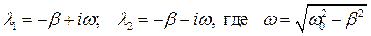
В этом случае решение дифференциального уравнения будет иметь вид:
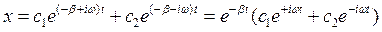
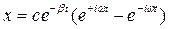 Коэффициенты c 1 и c 2 находим из начального условия x=0 в начальный момент времени t =0. Тогда c 1 = - c 2. Отсюда
Коэффициенты c 1 и c 2 находим из начального условия x=0 в начальный момент времени t =0. Тогда c 1 = - c 2. Отсюда
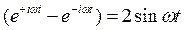 Вспоминая правила работы с комплексными числами заметим, что
Вспоминая правила работы с комплексными числами заметим, что
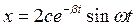 Отсюда наше решение приобретает вид
Отсюда наше решение приобретает вид
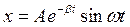
Обозначим 2с через А тогда
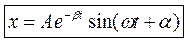 Здесь А имеет смысл начальной амплитуды колебания. Для большей общности решения его можно записать в виде
Здесь А имеет смысл начальной амплитуды колебания. Для большей общности решения его можно записать в виде
Здесь a начальная фаза колебания. Нетрудно проверить, подставив это выражение в дифференциальное уравнение колебаний, что это выражение является решением исходного уравнения.
Таким образом, мы видим, что колебания в колебательной системе с затуханием происходят так же по гармоническому закону. Однако величина максимального отклонения колеблющейся величины с течением времени уменьшается экспоненциально.
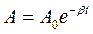
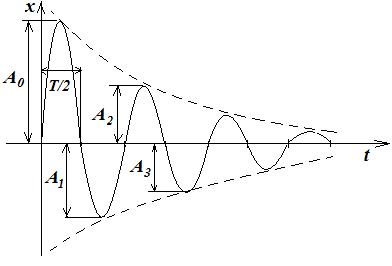
амплитуда колебаний в этом случае будет равна
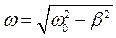 Скорость затухания амплитуды колебаний зависит от показателя экспоненты коэффициента затухания β = m /2 m, который обратен по величине времени за которое амплитуда колебаний уменьшится в е раз.
Скорость затухания амплитуды колебаний зависит от показателя экспоненты коэффициента затухания β = m /2 m, который обратен по величине времени за которое амплитуда колебаний уменьшится в е раз.
Затухающие колебания характеризуются частотой колебания
Как видим частота колебаний меньше частоты собственных колебаний без затухания.
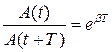 Уменьшение амплитуды затухающих колебаний с течением времени характеризуется декрементом затухания, который равен отношению амплитуд двух последующих через период колебаний.
Уменьшение амплитуды затухающих колебаний с течением времени характеризуется декрементом затухания, который равен отношению амплитуд двух последующих через период колебаний.
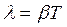 Натуральный логорифм от этого отношения называется логорифмическим декрементом затухания l
Натуральный логорифм от этого отношения называется логорифмическим декрементом затухания l
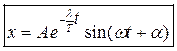 Для характеристики колебательного процесса обычно пользуются логорифмическим декрементом затухания
Для характеристики колебательного процесса обычно пользуются логорифмическим декрементом затухания
За время τ = 1/β система успеет совершить Ne = 1/l колебаний. Величина Q = pNe= p/l, называемая добротностью часто используется для характеристики колебательной системы. Действительно чем выше добротность, чем больше система совершит колебаний прежде чем они заметно затухнут, тем меньше трения в системе, тем меньше тратится энергии колебаний на трение.
Подставим закон колебания в выражение для полной энергии колебаний.
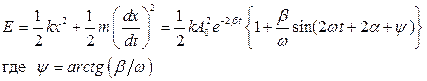
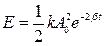 При малом затухании β<<w тригонометрическим членом в выражении можно пренебречь. В этом случае выражение для энергии примет вид
При малом затухании β<<w тригонометрическим членом в выражении можно пренебречь. В этом случае выражение для энергии примет вид
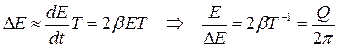 Убыль энергии за период в системе можно оценить как
Убыль энергии за период в системе можно оценить как
Отсюда видно, что добротность системы характеризует отношение убыли энергии в системе за один период колебаний к полной энергии колебаний системы.
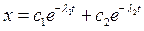 С ростом трения в системе частота колебаний снижается, а когда трение возрастает настолько, что становится β > w, решение дифференциального уравнения меняется.
С ростом трения в системе частота колебаний снижается, а когда трение возрастает настолько, что становится β > w, решение дифференциального уравнения меняется.
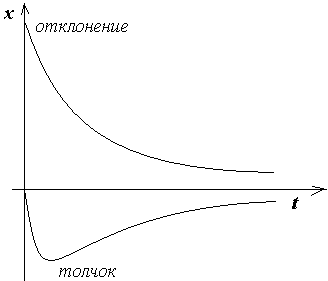
Это решение уже описывает не процесс колебаний, а чисто затухающий процесс в системе.
При этом если систему вывести из положения равновесия толчком или первоначально отклонив ее в положение равновесия она будет приходить по разному.
Вынужденные колебания
Рассмотрим ситуацию, когда на колебательную систему «с затуханием» действует периодическая сила изменяющаяся по гармоническому закону. В этом случае в дифференциальное уравнение приведенное в начале лекции и описывающее колебательный затухающий процесс необходимо добавить член отвечающий за силу действующую на систему и меняющуюся по гармоническому закону.
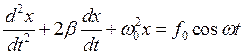
Если бы это неоднородное уравнение в правой части имело бы 0, то это было бы однородное уравнение. Решение неоднородного уравнения состоит из общего решения однородного уравнения и частного решения неоднородного уравнения.
Общее решение однородного уравнения, как нами было получено выше является
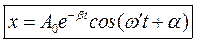
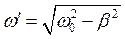
Где
Перейдем к нахождению частного решения неоднородного уравнения. Для этого представим вынуждающую силу в виде
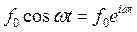
Тогда уравнение колебаний под действием вынуждающей силы можно представить как:
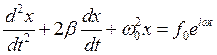
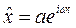
Будем искать частное решение в виде
Подставляя его в уравнение, получим:
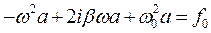
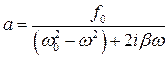
Отсюда получим
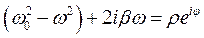
Комплексное число можно представить в виде:
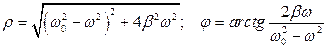
Где
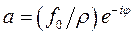
Отсюда
Тогда частное решение может быть записано в виде действительной части от выражения
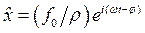
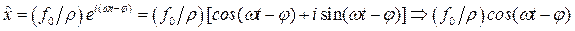
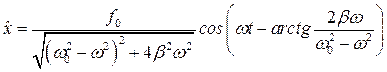
Отсюда общее решение состоящее из общего решения однородного уравнения и частного решения неоднородного будет иметь вид:
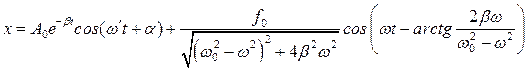
Таким образом, колебания системы с затуханием под действием периодически изменяющейся силы представимы в виде суммы двух функций. Первая, отражающая колебания системы с затуханием, затухает со временем. Вторая функция описывает колебания под действием непосредственно вынуждающей периодической силы.
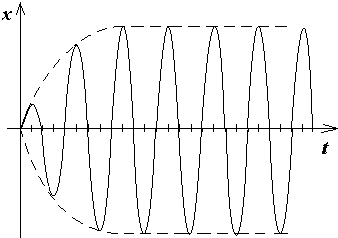
Заметим, что чем ближе частота колебаний вынуждающей силы к частоте собственных колебаний системы без трения, тем больше амплитуда вынужденных колебаний.
Определим в каком случае амплитуда вынужденных колебаний будет максимальна. В этом случае говорят, что наступает явление резонанса.
Для этого продифференцируем второй член в выражении описывающем вынужденные колебания по w и приравняем к нулю (первый член мы не принимаем во внимание и отбрасываем, так как он быстро затухает.
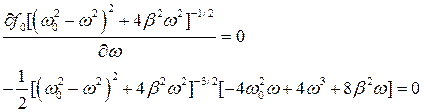
Из этого выражения видно, что максимальное свое значение колеблющаяся величина принимает либо когда частота силы вынуждающих систему колебаться превращается в ноль, что не соответствует условию задачи, либо когда
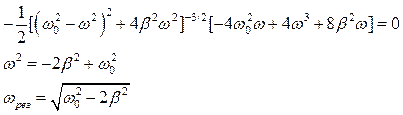
При этом максимальная амплитуда как легко видеть будет равна:
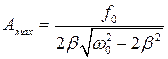
Явление резонанса является очень важным для техники. Его нужно учитывать во многих создаваемых инженерных конструкциях. Так как даже незначительное по мощности воздействие периодической силы действующей на конструкцию может оказаться для нее фатальным если частота колебания вынуждающей силы совпадает с частотой собственных колебаний системы.
Волны
Волновое движение. Интерференция волн от двух источников. Стоячая волна.
Пусть имеется некоторая точка, совершающая колебания в среде все частицы которой связаны между собой. Тогда энергия колебания может передаться и другим частицам вызывая их колебания.
Уравнение волны
Выясним каким образом можно аналитически характеризовать волновой процесс. Представим, что мы возбудили волну на веревке. Конец веревки мы привели в колебательное движение. Пусть веревка растянута вдоль оси у, тогда смещение веревки из нейтрального положения происходят в перпендикулярном у направлении по оси х . Пусть конец веревки колеблется по гармоническому закону x = acos w t. Произвольная точка лежащая на веревке с координатой у начнет колебаться с той же фазой с некоторым запаздыванием на время τ = у/ V фаз.
Таким образом уравнение колебания произвольной точки лежащей на пути распространения волны можно записать следующим образом:
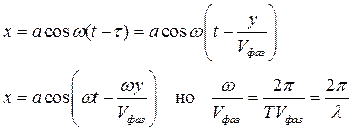
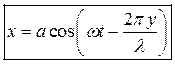
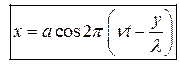
Каждая точка на луче волнового процесса совершает колебание во времени и имеет свою начальную фазу зависящую от ее геометрического места.
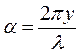
Таким образом если рассмотреть волновой процесс в какой то фиксированный момент времени, то видно, что колеблющаяся величина будет распределена вдоль луча периодически.
Две точки с координатами у1 и у2 имеют разность фаз a1-a2 = 2p(у2- у1)/l. Это так называется плоские волны.
Однако в упругой сплошной среде от точечного источника могут распространяться сферические волны, у которых амплитуда убывает обратно пропорционально расстоянию от источника.
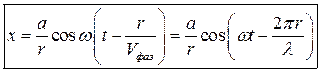
Интерференция волн
В среде могут распространяться колебания от нескольких источников. Если колебания от нескольких источников происходят с одинаковой частотой в одном направлении и постоянной разностью фаз, то такие колебания при наложении могут складываться. Это явление получило название интерференции, а такие колебания называются монохроматическими и когерентными.
Явление интерференции можно наблюдать в простом эксперименте. Возбудим в пространстве волну и поставим перед ее фронтом преграду в которой имеются два отверстия.
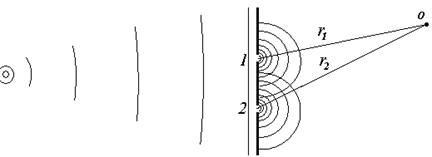
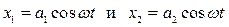 По принципу Гюйгенса каждая точка фронта волны сама по себе является источником вторичных волн. Таким образом, эти отверстия являются двумя источниками монохроматических когерентных волн:
По принципу Гюйгенса каждая точка фронта волны сама по себе является источником вторичных волн. Таким образом, эти отверстия являются двумя источниками монохроматических когерентных волн:
Рассмотрим некоторую точку О расположенную за преградой на расстоянии r1 и r2 соответственно от первого и второго отверстия. В этой точке колебания дошедшие от первого и второго отверстия будут иметь вид соответственно:
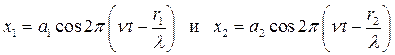
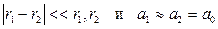
Если расстояние между отверстием 1 и 2 невелико, то
В этом случае, как мы уже знаем амплитуда результирующего колебания определяется из выражения:
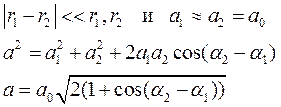
Таким образом, если
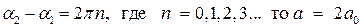
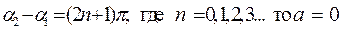 Если
Если
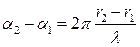
Отсюда учитывая, что
Получим условия максимума и минимума амплитуды результирующего колебания в произвольной точке за преградой:
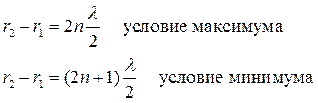
Результирующая картина называемая интерференционной представляет собой систему точек в которых имеет место усиление или ослабление колебаний.
Стоячие волны
Особым случаем интерференции являются так называемые стоячие волны образующиеся в результате наложения двух встречных плоских волн одинаковой амплитуды и частоты. В качестве примера рассмотрим стоячие волны образующиеся на струне.
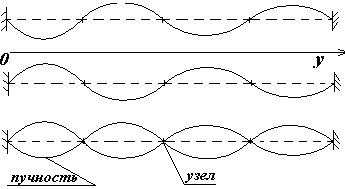
Пусть на струне закрепленной на концах в направлении оси у бежит плоская волна
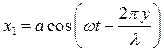
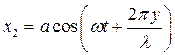 Добежав до закрепленного конца волна отразится от него и побежит в обратном направлении
Добежав до закрепленного конца волна отразится от него и побежит в обратном направлении
В результате эти волны складываются и результирующие колебания будут определятся новым выражением:
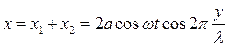
Первый сомножитель в этом выражении определяет частоту временных колебаний точек струны, второй сомножитель показывает пространственную периодичность максимумов (место пучности) и минимумов (узлов) амплитуды колебания точек струны.
Координаты пучности определяются из выражения
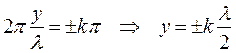
Расстояние между пучностями можно определить из выражения:
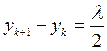
Координаты узлов и расстояние между ними соответственно определяются как:
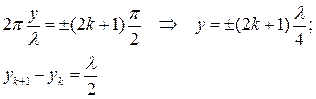
Лекция №5
Механика
Колебания
Затухающие колебания. Характеристики затухающих колебаний. Вынужденные колебания. Резонанс.
Затухающие колебания
 На предыдущей лекции мы рассмотрели примеры колебаний некоторых механических колебательных систем совершающих гармонические колебания. Мы рассмотрели случаи так называемых собственных колебаний. То есть таких колебаний, которые совершаются без постоянного внешнего воздействия и которые потому называются собственными. В наших примерах колебания в рассматриваемых системах происходит с постоянной во времени амплитудой и частотой колебания. Это так называемые незатухающие колебания. Однако в реальности в любой колебательной системе присутствует трение, приводящее к потере энергии колебательного процесса, поэтому колебания в любой реальной колебательной системе затухают. Разберем пример затухающих колебаний.
На предыдущей лекции мы рассмотрели примеры колебаний некоторых механических колебательных систем совершающих гармонические колебания. Мы рассмотрели случаи так называемых собственных колебаний. То есть таких колебаний, которые совершаются без постоянного внешнего воздействия и которые потому называются собственными. В наших примерах колебания в рассматриваемых системах происходит с постоянной во времени амплитудой и частотой колебания. Это так называемые незатухающие колебания. Однако в реальности в любой колебательной системе присутствует трение, приводящее к потере энергии колебательного процесса, поэтому колебания в любой реальной колебательной системе затухают. Разберем пример затухающих колебаний.
Рассмотрим колебания пружинного маятника погруженного в какую либо жидкость. (Строго говоря, даже воздушную среду можно считать некоей сплошной средой, жидкостью). Любая жидкость обладает вязкостью, которое определяет трение движущихся твердых тел. Эта сила трения при малых скоростях пропорциональна скорости тела. Таким образом, уравнение колебаний пружинного маятника с учетом сил трения будет выглядеть как: md 2 x / dt 2 = - m dx / dt - kx.
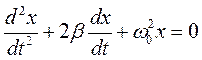 Разделим обе части уравнения на m и перенесем все члены в левую часть, после чего обозначив m / m и k / m через 2β и w 0 2 соответственно, получим дифференциальное уравнение, описывающее колебания в механической системе с вязким трением.
Разделим обе части уравнения на m и перенесем все члены в левую часть, после чего обозначив m / m и k / m через 2β и w 0 2 соответственно, получим дифференциальное уравнение, описывающее колебания в механической системе с вязким трением.
Отметим, что w 0 это та частота, с которой система бы совершала колебания в отсутствии трения. Это частота собственных колебаний системы.
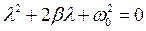 Решение полученного дифференциального уравнения будем искать в виде x ~ e l t. Подставляя это выражение в наше уравнение и произведя необходимое дифференцирование и сокращение, получим
Решение полученного дифференциального уравнения будем искать в виде x ~ e l t. Подставляя это выражение в наше уравнение и произведя необходимое дифференцирование и сокращение, получим
Это уравнение получило название характеристического уравнение. Решая это уравнение относительно l получим его значение при котором выбранный нами вид функции превращает дифференциальное уравнение в тождество. Таким образом, выбранная нами функция превращается в решение дифференциального уравнения.
Характеристическоое уравнения имеет два корня, которые равны:
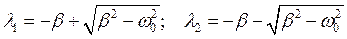
Пусть затухание будет слабым таким, чтобы β < w 0 тогда преобразуем корень и получим
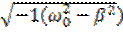 обозначим
обозначим 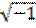 как i и
как i и 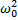 - β2 обозначим как ω2
- β2 обозначим как ω2
тогда 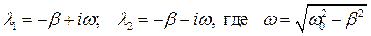
В этом случае решение дифференциального уравнения будет иметь вид:
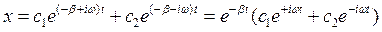
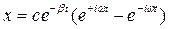 Коэффициенты c 1 и c 2 находим из начального условия x=0 в начальный момент времени t =0. Тогда c 1 = - c 2. Отсюда
Коэффициенты c 1 и c 2 находим из начального условия x=0 в начальный момент времени t =0. Тогда c 1 = - c 2. Отсюда
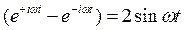 Вспоминая правила работы с комплексными числами заметим, что
Вспоминая правила работы с комплексными числами заметим, что
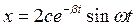 Отсюда наше решение приобретает вид
Отсюда наше решение приобретает вид
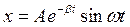
Обозначим 2с через А тогда
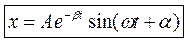 Здесь А имеет смысл начальной амплитуды колебания. Для большей общности решения его можно записать в виде
Здесь А имеет смысл начальной амплитуды колебания. Для большей общности решения его можно записать в виде
Здесь a начальная фаза колебания. Нетрудно проверить, подставив это выражение в дифференциальное уравнение колебаний, что это выражение является решением исходного уравнения.
Таким образом, мы видим, что колебания в колебательной системе с затуханием происходят так же по гармоническому закону. Однако величина максимального отклонения колеблющейся величины с течением времени уменьшается экспоненциально.
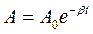

амплитуда колебаний в этом случае будет равна
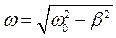 Скорость затухания амплитуды колебаний зависит от показателя экспоненты коэффициента затухания β = m /2 m, который обратен по величине времени за которое амплитуда колебаний уменьшится в е раз.
Скорость затухания амплитуды колебаний зависит от показателя экспоненты коэффициента затухания β = m /2 m, который обратен по величине времени за которое амплитуда колебаний уменьшится в е раз.
Затухающие колебания характеризуются частотой колебания
Как видим частота колебаний меньше частоты собственных колебаний без затухания.
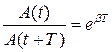 Уменьшение амплитуды затухающих колебаний с течением времени характеризуется декрементом затухания, который равен отношению амплитуд двух последующих через период колебаний.
Уменьшение амплитуды затухающих колебаний с течением времени характеризуется декрементом затухания, который равен отношению амплитуд двух последующих через период колебаний.
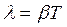 Натуральный логорифм от этого отношения называется логорифмическим декрементом затухания l
Натуральный логорифм от этого отношения называется логорифмическим декрементом затухания l
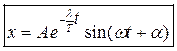 Для характеристики колебательного процесса обычно пользуются логорифмическим декрементом затухания
Для характеристики колебательного процесса обычно пользуются логорифмическим декрементом затухания
За время τ = 1/β система успеет совершить Ne = 1/l колебаний. Величина Q = pNe= p/l, называемая добротностью часто используется для характеристики колебательной системы. Действительно чем выше добротность, чем больше система совершит колебаний прежде чем они заметно затухнут, тем меньше трения в системе, тем меньше тратится энергии колебаний на трение.
Подставим закон колебания в выражение для полной энергии колебаний.
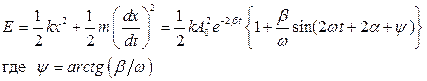
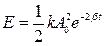 При малом затухании β<<w тригонометрическим членом в выражении можно пренебречь. В этом случае выражение для энергии примет вид
При малом затухании β<<w тригонометрическим членом в выражении можно пренебречь. В этом случае выражение для энергии примет вид
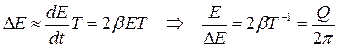 Убыль энергии за период в системе можно оценить как
Убыль энергии за период в системе можно оценить как
Отсюда видно, что добротность системы характеризует отношение убыли энергии в системе за один период колебаний к полной энергии колебаний системы.
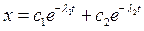 С ростом трения в системе частота колебаний снижается, а когда трение возрастает настолько, что становится β > w, решение дифференциального уравнения меняется.
С ростом трения в системе частота колебаний снижается, а когда трение возрастает настолько, что становится β > w, решение дифференциального уравнения меняется.
Это решение уже описывает не процесс колебаний, а чисто затухающий процесс в системе.
При этом если систему вывести из положения равновесия толчком или первоначально отклонив ее в положение равновесия она будет приходить по разному.

Вынужденные колебания
Рассмотрим ситуацию, когда на колебательную систему «с затуханием» действует периодическая сила изменяющаяся по гармоническому закону. В этом случае в дифференциальное уравнение приведенное в начале лекции и описывающее колебательный затухающий процесс необходимо добавить член отвечающий за силу действующую на систему и меняющуюся по гармоническому закону.
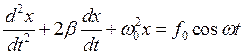
Если бы это неоднородное уравнение в правой части имело бы 0, то это было бы однородное уравнение. Решение неоднородного уравнения состоит из общего решения однородного уравнения и частного решения неоднородного уравнения.
Общее решение однородного уравнения, как нами было получено выше является
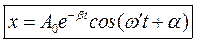
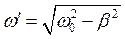
Где
Перейдем к нахождению частного решения неоднородного уравнения. Для этого представим вынуждающую силу в виде
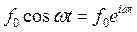
Тогда уравнение колебаний под действием вынуждающей силы можно представить как:
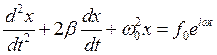
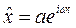
Будем искать частное решение в виде
Подставляя его в уравнение, получим:
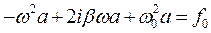
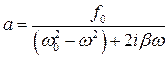
Отсюда получим
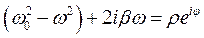
Комплексное число можно представить в виде:
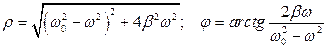
Где
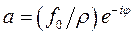
Отсюда
Тогда частное решение может быть записано в виде действительной части от выражения
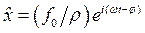
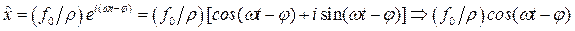
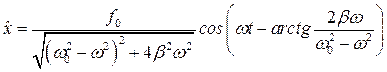
Отсюда общее решение состоящее из общего решения однородного уравнения и частного решения неоднородного будет иметь вид:
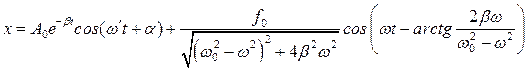
Таким образом, колебания системы с затуханием под действием периодически изменяющейся силы представимы в виде суммы двух функций. Первая, отражающая колебания системы с затуханием, затухает со временем. Вторая функция описывает колебания под действием непосредственно вынуждающей периодической силы.

Заметим, что чем ближе частота колебаний вынуждающей силы к частоте собственных колебаний системы без трения, тем больше амплитуда вынужденных колебаний.
Определим в каком случае амплитуда вынужденных колебаний будет максимальна. В этом случае говорят, что наступает явление резонанса.
Для этого продифференцируем второй член в выражении описывающем вынужденные колебания по w и приравняем к нулю (первый член мы не принимаем во внимание и отбрасываем, так как он быстро затухает.
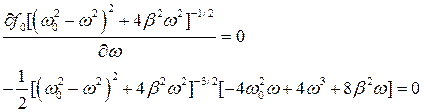
Из этого выражения видно, что максимальное свое значение колеблющаяся величина принимает либо когда частота силы вынуждающих систему колебаться превращается в ноль, что не соответствует условию задачи, либо когда
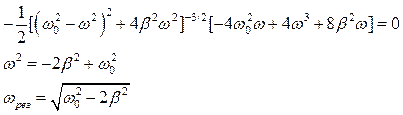
При этом максимальная амплитуда как легко видеть будет равна:
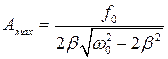
Явление резонанса является очень важным для техники. Его нужно учитывать во многих создаваемых инженерных конструкциях. Так как даже незначительное по мощности воздействие периодической силы действующей на конструкцию может оказаться для нее фатальным если частота колебания вынуждающей силы совпадает с частотой собственных колебаний системы.
Представление колебаний с помощью векторной диаграммы. Сложение однонаправленных колебаний. Биения. Сложение колебаний колеблющихся в ортогональных плоскостях.
Особым случаем является процесс, при котором происходит сложение колебаний, при этом результирующим явлением будет тоже колебательный, но более сложный процесс. Рассмотрим случай сложения двух колебаний.
Колебания, из которых будет складываться результирующий процесс, могут быть однонаправленными и ортогональными (взаимно перпендикулярными). Нахождение результирующего колебания по известным параметрам исходных колебаний происходит по определенным правилам. Познакомимся с ними и начнем с однонаправленных колебаний.
Гармонические колебания могут быть представлены графическим способом на векторной диаграмме. Обозначим точку 0 через нее проведем ось х. Из точки 0 под некоторым углом a к оси х проведем вектор длиной а. Пусть вектор а вращается вокруг точки 0 с угловой скоростью w 0. В этом случае величина проекции х вектора а на ось х может быть выражена уравнением:
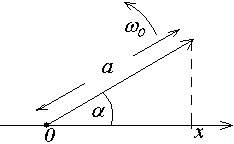
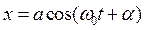
Следовательно, проекция конца вектора а будет совершать гармонические колебания с амплитудой а равной длине вектора, с начальной фазой равной начальному углу a между вектором и осью х и частотой колебаний равной угловой скорости w 0 вращения вектора.
Рассмотрим сложение двух гармонических однонаправленных колебаний.
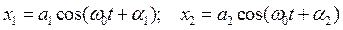
Изобразим эти гармонические колебания на векторной диаграмме:
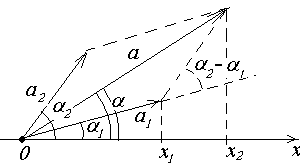
Частота вращения векторов а1 и а2 одинакова и равна w 0 поэтому такой же будет частота вращения результирующего вектора. Вектора подчиняются правилу векторного сложения, поэтому результирующий вектор а будет равен векторной сумме исходных векторов а1 и а2 . Его величина будет равна диагонали параллелограмма стороны которого составляют исходные вектора.
Таким образом, величина результирующего вектора (амплитуда результирующего колебания):
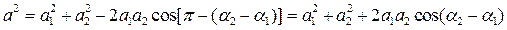
При этом начальная фаза колебания находится из выражения:
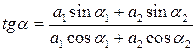
Таким образом, результирующее колебание описывается выражением
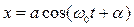
Где амплитуда частота и начальная фаза колебания определяется выражениями описанными выше.
Если частота колебаний двух процессов неодинакова в результате получаются сложные негармонические колебания.
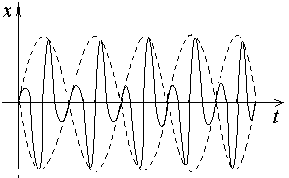
Особым является случай, когда складываются два однонаправленных гармонических колебания со слабо различающейся частотой.
Представим частоты двух колебаний, как w и w + D w, где D w << w. Для простоты будем полагать амплитуды колебаний одинаковыми и равными а, а так же положим, что начальная фаза обоих колебаний равна нулю.
В том случае рассматриваемые колебания можно описать выражениями:
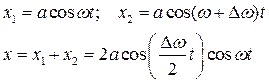
Во втором сомножителе мы пренебрегли малой величиной D w /2 в сравнении с w.
Таким образом, результирующие колебания могут быть представлены как гармонические колебания с частотой w и амплитудой зависящей от времени по периодическому закону и равной половине разности частот складываемых колебаний.
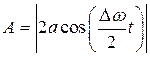



 На предыдущей лекции мы рассмотрели примеры колебаний некоторых механических колебательных систем совершающих гармонические колебания. Мы рассмотрели случаи так называемых собственных колебаний. То есть таких колебаний, которые совершаются без постоянного внешнего воздействия и которые потому называются собственными. В наших примерах колебания в рассматриваемых системах происходит с постоянной во времени амплитудой и частотой колебания. Это так называемые незатухающие колебания. Однако в реальности в любой колебательной системе присутствует трение, приводящее к потере энергии колебательного процесса, поэтому колебания в любой реальной колебательной системе затухают. Разберем пример затухающих колебаний.
На предыдущей лекции мы рассмотрели примеры колебаний некоторых механических колебательных систем совершающих гармонические колебания. Мы рассмотрели случаи так называемых собственных колебаний. То есть таких колебаний, которые совершаются без постоянного внешнего воздействия и которые потому называются собственными. В наших примерах колебания в рассматриваемых системах происходит с постоянной во времени амплитудой и частотой колебания. Это так называемые незатухающие колебания. Однако в реальности в любой колебательной системе присутствует трение, приводящее к потере энергии колебательного процесса, поэтому колебания в любой реальной колебательной системе затухают. Разберем пример затухающих колебаний.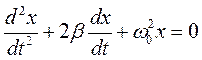 Разделим обе части уравнения на m и перенесем все члены в левую часть, после чего обозначив m / m и k / m через 2β и w 0 2 соответственно, получим дифференциальное уравнение, описывающее колебания в механической системе с вязким трением.
Разделим обе части уравнения на m и перенесем все члены в левую часть, после чего обозначив m / m и k / m через 2β и w 0 2 соответственно, получим дифференциальное уравнение, описывающее колебания в механической системе с вязким трением.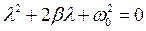 Решение полученного дифференциального уравнения будем искать в виде x ~ e l t. Подставляя это выражение в наше уравнение и произведя необходимое дифференцирование и сокращение, получим
Решение полученного дифференциального уравнения будем искать в виде x ~ e l t. Подставляя это выражение в наше уравнение и произведя необходимое дифференцирование и сокращение, получим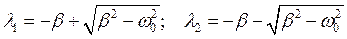
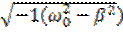 обозначим
обозначим 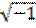 как i и
как i и 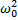 - β2 обозначим как ω2
- β2 обозначим как ω2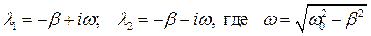
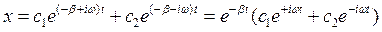
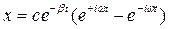 Коэффициенты c 1 и c 2 находим из начального условия x=0 в начальный момент времени t =0. Тогда c 1 = - c 2. Отсюда
Коэффициенты c 1 и c 2 находим из начального условия x=0 в начальный момент времени t =0. Тогда c 1 = - c 2. Отсюда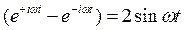 Вспоминая правила работы с комплексными числами заметим, что
Вспоминая правила работы с комплексными числами заметим, что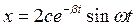 Отсюда наше решение приобретает вид
Отсюда наше решение приобретает вид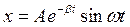
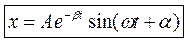 Здесь А имеет смысл начальной амплитуды колебания. Для большей общности решения его можно записать в виде
Здесь А имеет смысл начальной амплитуды колебания. Для большей общности решения его можно записать в виде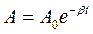

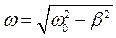 Скорость затухания амплитуды колебаний зависит от показателя экспоненты коэффициента затухания β = m /2 m, который обратен по величине времени за которое амплитуда колебаний уменьшится в е раз.
Скорость затухания амплитуды колебаний зависит от показателя экспоненты коэффициента затухания β = m /2 m, который обратен по величине времени за которое амплитуда колебаний уменьшится в е раз.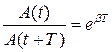 Уменьшение амплитуды затухающих колебаний с течением времени характеризуется декрементом затухания, который равен отношению амплитуд двух последующих через период колебаний.
Уменьшение амплитуды затухающих колебаний с течением времени характеризуется декрементом затухания, который равен отношению амплитуд двух последующих через период колебаний.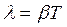 Натуральный логорифм от этого отношения называется логорифмическим декрементом затухания l
Натуральный логорифм от этого отношения называется логорифмическим декрементом затухания l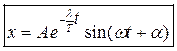 Для характеристики колебательного процесса обычно пользуются логорифмическим декрементом затухания
Для характеристики колебательного процесса обычно пользуются логорифмическим декрементом затухания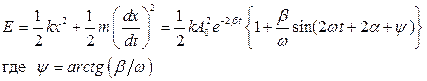
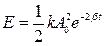 При малом затухании β<<w тригонометрическим членом в выражении можно пренебречь. В этом случае выражение для энергии примет вид
При малом затухании β<<w тригонометрическим членом в выражении можно пренебречь. В этом случае выражение для энергии примет вид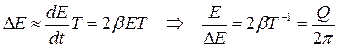 Убыль энергии за период в системе можно оценить как
Убыль энергии за период в системе можно оценить как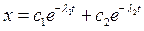 С ростом трения в системе частота колебаний снижается, а когда трение возрастает настолько, что становится β > w, решение дифференциального уравнения меняется.
С ростом трения в системе частота колебаний снижается, а когда трение возрастает настолько, что становится β > w, решение дифференциального уравнения меняется.
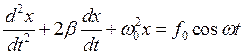
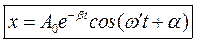
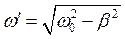
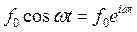
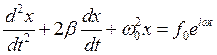
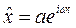
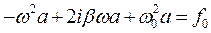
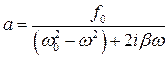
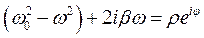
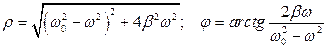
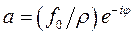
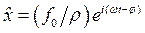
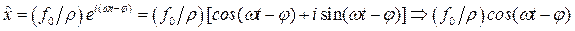
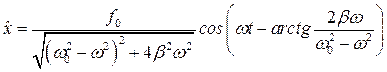
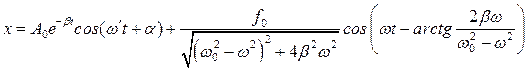

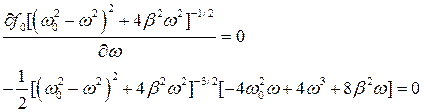
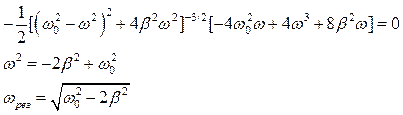
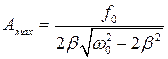
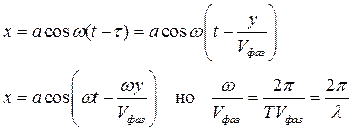
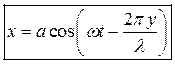
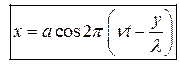
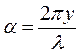
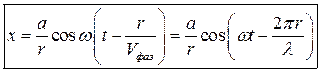

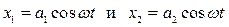 По принципу Гюйгенса каждая точка фронта волны сама по себе является источником вторичных волн. Таким образом, эти отверстия являются двумя источниками монохроматических когерентных волн:
По принципу Гюйгенса каждая точка фронта волны сама по себе является источником вторичных волн. Таким образом, эти отверстия являются двумя источниками монохроматических когерентных волн: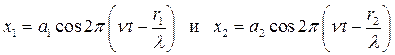
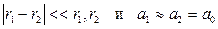
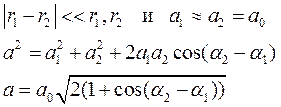
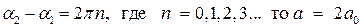
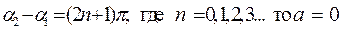 Если
Если 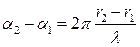
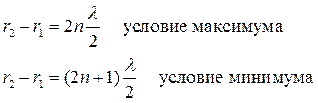

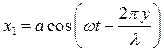
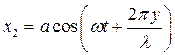 Добежав до закрепленного конца волна отразится от него и побежит в обратном направлении
Добежав до закрепленного конца волна отразится от него и побежит в обратном направлении