(В параграфе 4 будет озвучено еще одно соотношение, относящееся к математической модели континуальных тел)
Нетрудно видеть, что в этом постулате, скрылись сразу все 3 закона Ньютона, однако понятие материальной точки в явном виде тут не фигурирует. Таким образом удалось совершить переход от не строго определенного понятия материальной точки, к параметрам, сопоставляемым геометрической точке. В дальнейшем изложении будет показано, что в конечном результате, такой подход будет давать те-же уравнения, что были получены в концепции материальных точек.
Помимо прочего, будет видно, что способ “материальных точек” есть не что иное, как вычислительный метод, в рамках описанной теории, который в своей сущности представляет численное стремление суммы к интегралу.
Динамика поступательного движения
Проинтегрируем выражение: ρ  =
= 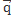 по всей длине тела:
по всей длине тела:
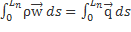 =
= 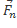
Назовем точку, с радиус вектором:  =
=  центром масс тела.
центром масс тела.
Соответственно 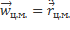 =
= 
 .
.
Следовательно: 
Последнее уравнение назовем основным уравнением динамики поступательного движения.
Динамика вращательного движения
Назовем Импульсом точки тела величину 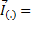 ρ
ρ 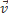
Назовем Импульсом тела величину 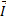 =
= 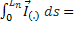
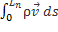 =
= 
Заметим, импульс тела это 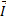 = m
= m 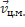
Назовем Кинетическим моментом точки величину 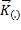 =
= 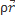
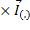 , где
, где 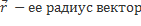
Назовем Кинетическим моментом тела величину 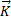 =
=  =
= 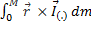
Векторно домножим обе части равенства ρ  =
= 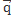 на
на 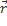 слева.
слева.
ρ 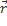

 =
= 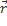
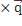 =
= 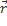
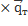 +
+ 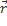

Где 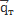 интенсивность внутрених сил, а
интенсивность внутрених сил, а 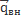 интенсивность внешних сил.
интенсивность внешних сил.
(Пояснение: 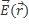 =
= 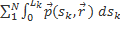 =
= 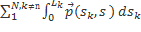 +
+ 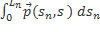
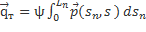 ,
, 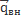 =
= 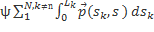 ,
, 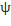 =
=  ))
))
ρ 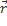

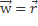
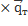 +
+ 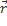

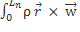 ds =
ds = 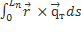 +
+ 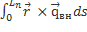
Заметим: 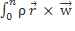 ds =
ds = 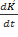
Если взаимодействие центральное, то есть для любых двух точек тела вектора  лежат на линии соединяющей эти точки, то нетрудно показать, что
лежат на линии соединяющей эти точки, то нетрудно показать, что 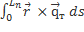 = 0
= 0
Действительно: 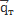 =
= 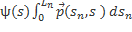
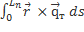 =
= 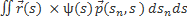 = -
= - 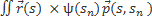 ds d
ds d 
В интеграле 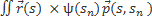 ds d
ds d  переименуем переменные s->
переименуем переменные s->  ,
,  ->s
->s
Тогда 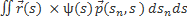 = -
= -  ds d
ds d 
Если А=В, то А = 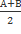 , следовательно:
, следовательно:
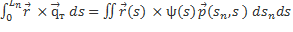 =
= 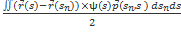
В случае центрального взаимодействия точек континуума 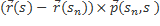 = 0
= 0
Таким образом получаем: 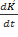 =
= 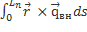
Величину 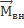 =
= 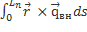 назовем моментом внешних сил.
назовем моментом внешних сил.
В общем случае уравнение  =
= 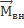 является частью аксиоматического построения континуума.
является частью аксиоматического построения континуума.
Таким образом мы понимаем, что вращательное движение сводится к поступательному лишь в частных случаях.
В случае, если твердое тело вращается вокруг своей оси это выражение принимает вид: 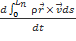 =
= 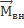
Тогда с учетом того, что 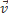 (t)
(t)  (t) =
(t) =  ,
, 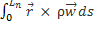 =
= 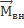
 =
= 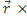
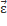 , где
, где 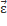 -угловое ускорение тела.
-угловое ускорение тела.
Заметим: 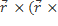
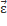 ) =
) = 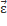
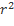
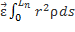 =
= 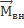
Величину I = 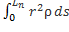 назовем моментом инерции тела относительно не подвижного начала.
назовем моментом инерции тела относительно не подвижного начала.
Отметим, что справедлива такая же формула, написанная относительно центра масс.
Теорема
Формула 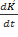 =
= 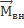 остается верной, если считать её относительно центра масс.
остается верной, если считать её относительно центра масс.
Доказательство
Пусть 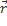 – радиус вектор точки,
– радиус вектор точки, 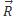 – радиус вектор, отложенный от центра масс и
– радиус вектор, отложенный от центра масс и  – радиус вектор центра масс. Они, очевидно, связанны равенством:
– радиус вектор центра масс. Они, очевидно, связанны равенством: 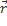 =
=  +
+  .
.
1)Кинетический момент относительно центра масс.
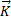 =
=  =
= 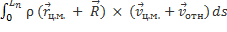
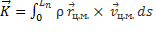 +
+  +
+  +
+ 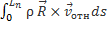
Интеграл:  = 0, действительно:
= 0, действительно:
 =
= 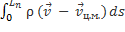 =
= 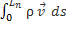 -
- 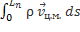
 =
= 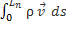 - m
- m 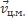 = m
= m 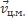 - m
- m 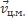 = 0
= 0
Следовательно второй интеграл  = 0
= 0
 = -
= -  = -
= - 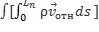 dt = 0
dt = 0
Обозначим 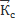 =
= 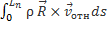 -кинетический момент относительно центра масс.
-кинетический момент относительно центра масс.
Таким образом:  +
+ 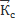
2)Момент сил относительно центра масс.
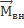 =
= 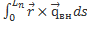 =
= 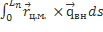 +
+ 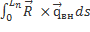
Обозначим 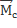 =
= 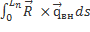 – момент внешних сил относительно центра масс.
– момент внешних сил относительно центра масс.
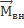 =
= 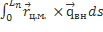 +
+ 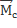
3) Таким образом:

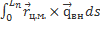 +
+ 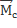 =
= 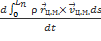 +
+ 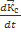
Так как:
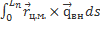 =
= 
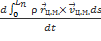 =
= 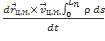 =
= 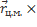
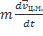 =
= 
То: 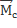 =
= 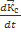
Ч.т.д.
Работа и Энергия
Введем понятие плотности работы b при перемещении точки тела за время  : b=
: b= 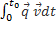
Введем понятие работы при перемещении тела: A = 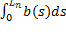
Введем понятие кинетической энергии: 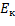 =
= 
Теорема №1
Если тело твердое и совершает плоские движения (не изменяет ось вращения), то кинетическая энергия представима в виде:
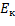 =
=  +
+ 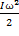
Где I - момент инерции относительно центра масс.
Доказательство
Рассмотрим плоское движение ТТ (твердого тела). Возьмем за полюс центр масс.
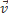 (s) =
(s) = 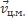 +
+ 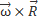
Где
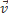 (s) -скорость точки с криволинейной координатой s.
(s) -скорость точки с криволинейной координатой s.
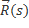 -радиус вектор точки с криволинейной координатой s, опущенный из центра масс.
-радиус вектор точки с криволинейной координатой s, опущенный из центра масс.
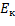 =
= 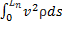 =
= 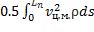 +
+ 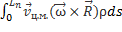 + 0.5
+ 0.5 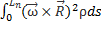
Первый интеграл:
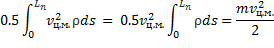
Второй интеграл сводится к уже рассмотренному в параграфе 4:
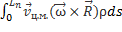 =
= 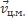
 =
= 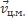
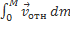 = 0
= 0
Третий интеграл:
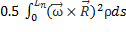 =
= 
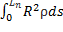 =
= 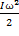
(Тут момент инерции считается относительно центра масс)
Ч.т.д.
Теорема №2
Для твердых тел, совершающих плоские движения верно:
1) 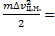

2) 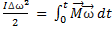
Доказательство
1) m 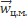 =
= 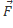
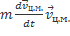 =
= 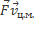
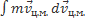 =
= 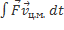
ð 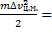

2) 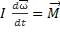
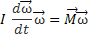
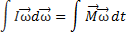
ð 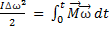
Ч.т.д.
Теорема №3
Для любого твердого тела, совершившего плоское перемещение верно:
A = 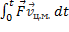 +
+ 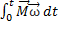
Доказательство
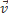 (s) =
(s) = 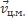 +
+ 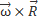
b= 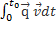 = b=
= b= 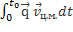 +
+ 
A= 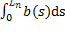
A= 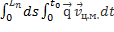 +
+  (повторные интегралы)
(повторные интегралы)
A= 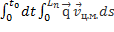 +
+ 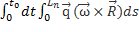
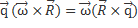
A=  +
+ 
A = 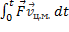 +
+ 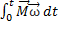
Ч.т.д.
Теорема №4
Для твердых тел, совершающих плоские движения верно: A= 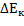
Доказательство
По теореме №1: 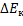 =
= 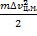 +
+ 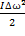
По теореме №2: 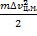 +
+ 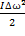 =
=  +
+ 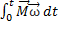
По теореме №3: А = 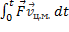 +
+ 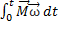
Таким образом: A= 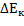
Ч.т.д.
Потенциальная энергия
Назовем потенциальным такое взаимодействие, для которого плотность работы b= 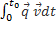 по произвольному перемещению точки тела, не зависит от времени и траектории перемещения, а зависит только от начального и конечного положения точки тела.
по произвольному перемещению точки тела, не зависит от времени и траектории перемещения, а зависит только от начального и конечного положения точки тела.
Теорема №1
Плотность работы потенциального поля по перемещению точки по замкнутому контору равна 0.
Доказательство
Произведем перемещение из точки 0 в нее же через точку 1. Тогда:
 +
+ 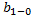 =
= 
Произведем перемещение из точки 0 в нее же через точку 1 дважды. Тогда:
 +
+ 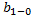 +
+  +
+ 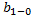 =
= 
Поскольку =  не зависит от способа перемещения, то:
не зависит от способа перемещения, то:
 +
+ 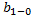 +
+  +
+ 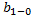 =
=  =
=  +
+ 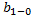
То есть:  +
+ 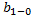 = 0
= 0
Рассмотрим точки 0, 1, 2 тогда:
 +
+  +
+ 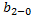 =
=  =
=  +
+ 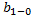 = 0
= 0
Совершенно ясно, что какое бы количество точек мы не рассмотрели бы, если перемещение по ним задает замкнутый контур, то в итоге плотность работы по перемещению в этом контуре будет равна 0.
Замечание:
Из доказанного следует что для любых трех точек 0,1,2 верно: 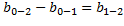
Определение:
Назовем плотностью потенциальной энергии точки, плотность работы по перемещению этой точки из (произвольно выбранного) нулевого положения в данное.
Будем писать:  =
= 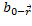
Где радиус вектором 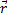 задается текущее положение точки тела.
задается текущее положение точки тела.
Назовем потенциальной энергией тела величину U = 
Теорема №2
Работа потенциальных сил по перемещению тела равна убыли потенциальной энергии.
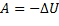
Доказательство:
При перемещении тела каждая его точка перемещается из начального, назовем его положение 1, в конечное, назовем его положение 2. Тогда для каждой точке тела существует функция:
 (s) =
(s) = 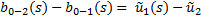 (s)
(s)
Проинтегрируем по длине тела:
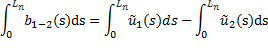
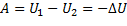
Ч.т.д.
Назовем полной механической энергией величину 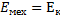 +
+ 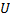
Теорема №3
В поле потенциального взаимодействия 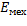 = const
= const
Доказательство:
Пусть тело переместилось и потенциальное поле совершило работу А, тогда:
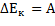 ,
, 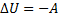 =>
=> 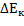 +
+ 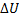 = 0 =>
= 0 =>  +
+ 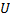 =const =>
=const => 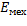 = const
= const
Ч.т.д.
§6.0 Определение 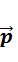 и ψ в частных случаях.
и ψ в частных случаях.



 =
= 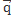 по всей длине тела:
по всей длине тела: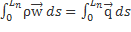 =
= 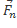
 =
=  центром масс тела.
центром масс тела.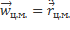 =
= 
 .
.
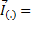 ρ
ρ 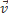
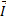 =
= 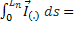
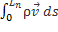 =
= 
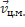
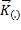 =
= 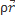
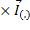 , где
, где 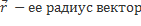
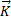 =
=  =
= 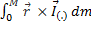
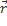 слева.
слева.
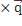 =
= 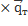 +
+ 
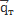 интенсивность внутрених сил, а
интенсивность внутрених сил, а 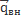 интенсивность внешних сил.
интенсивность внешних сил.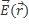 =
= 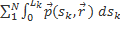 =
= 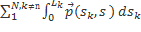 +
+ 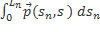
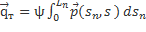 ,
, 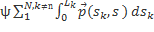 ,
, 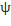 =
=  ))
))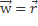
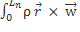 ds =
ds = 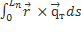 +
+ 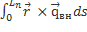
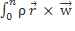 ds =
ds = 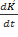
 лежат на линии соединяющей эти точки, то нетрудно показать, что
лежат на линии соединяющей эти точки, то нетрудно показать, что 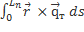 = 0
= 0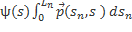
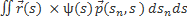 = -
= - 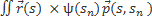 ds d
ds d 
 ->s
->s ds d
ds d 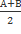 , следовательно:
, следовательно: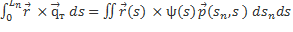 =
= 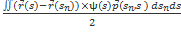
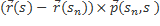 = 0
= 0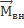 =
=  =
= 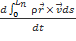 =
=  (t) =
(t) =  ,
, 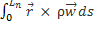 =
=  =
= 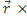
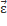 , где
, где 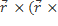
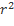
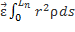 =
= 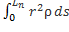 назовем моментом инерции тела относительно не подвижного начала.
назовем моментом инерции тела относительно не подвижного начала.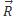 – радиус вектор, отложенный от центра масс и
– радиус вектор, отложенный от центра масс и  .
. =
= 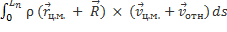
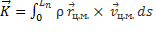 +
+  +
+  +
+ 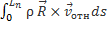
 = 0, действительно:
= 0, действительно: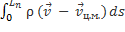 =
= 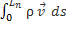 -
- 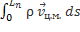
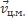 = m
= m  = -
= - 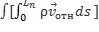 dt = 0
dt = 0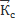 =
=  +
+ 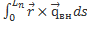 =
= 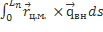 +
+ 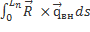
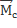 =
= 
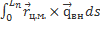 +
+ 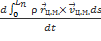 +
+ 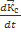

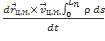 =
= 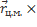
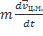 =
=  : b=
: b= 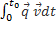
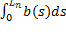
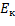 =
= 
 +
+ 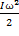
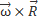
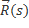 -радиус вектор точки с криволинейной координатой s, опущенный из центра масс.
-радиус вектор точки с криволинейной координатой s, опущенный из центра масс.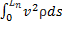 =
= 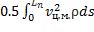 +
+ 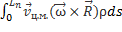 + 0.5
+ 0.5 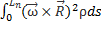
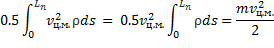
 =
= 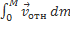 = 0
= 0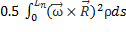 =
= 
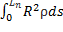 =
= 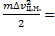

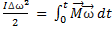
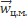 =
= 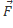
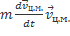 =
= 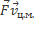
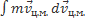 =
= 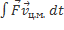
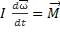
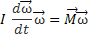
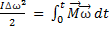
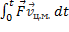 +
+ 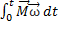
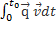 = b=
= b= 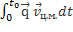 +
+ 
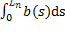
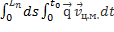 +
+  (повторные интегралы)
(повторные интегралы)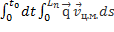 +
+ 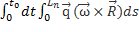
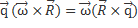
 +
+ 
 =
= 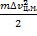 +
+ 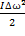
 +
+ 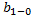 =
= 
 +
+ 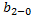 =
= 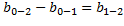
 =
= 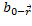
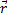 задается текущее положение точки тела.
задается текущее положение точки тела.
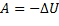
 (s) =
(s) = 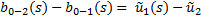 (s)
(s)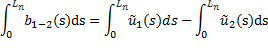
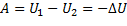
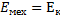 +
+ 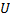
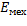 = const
= const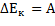 ,
, 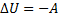 =>
=> 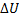 = 0 =>
= 0 =>  +
+ 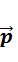 и ψ в частных случаях.
и ψ в частных случаях.


