Результаты, полученные при статистическом описании макроскопических систем, как и любые предсказания теории, требуют экспериментальной проверки. В эксперименте, как правило, регистрируются молекулы, летящие в одну сторону. Поэтому возникает практический интерес к определению составляющих скоростей молекул вдоль определенных направлений, например, вдоль оси 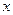 :
: 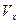 .
.
3.1. Распределение по проекциям скорости.
Для получения распределения по проекциям скоростей мы должны воспользоваться функцией микрораспределения, поскольку нас интересует вероятность молекуле иметь кинетическую энергию в интервале от 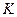 до
до 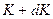 , обладая при этом определенными проекциями скоростей:
, обладая при этом определенными проекциями скоростей:
( ).
).
Вероятность молекуле идеального газа иметь определенную энергию равна произведению функции распределения Гиббса при  на соответствующий фазовый объем
на соответствующий фазовый объем  :
:
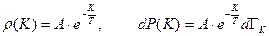 (3.1)
(3.1)
Рассмотрим подсистему, состоящую из одной молекулы, с кинетической энергией  и запишем её фазовый объем в пространстве скоростей:
и запишем её фазовый объем в пространстве скоростей:  .
.
Постоянная  уже была определена в предыдущем параграфе из условия нормировки.
уже была определена в предыдущем параграфе из условия нормировки.
Вероятность молекуле иметь кинетическую энергию в интервале от 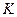 до
до 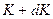 , обладая при этом определенными проекциями скоростей на оси координат:
, обладая при этом определенными проекциями скоростей на оси координат:

определяется выражением:
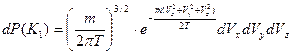 (3.2)
(3.2)
Поскольку координатные оси ортогональны и соответствующие проекции скоростей независимы, эту вероятность можно представить в виде произведения:
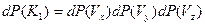 ,
,
где каждый из сомножителей представляет собой распределение Максвелла (1859 г.) для проекций скорости молекул.
Например.
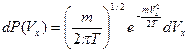 (3.3)
(3.3)
Т.о., распределение Максвелла по  ой проекции скорости:
ой проекции скорости:
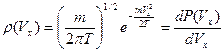 . (3.4)
. (3.4)
Это распределение симметрично относительно начала
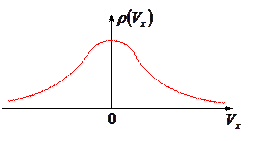 координат и имеет максимум при проекции скорости
координат и имеет максимум при проекции скорости
 . Положительные и отрицательные значения
. Положительные и отрицательные значения 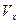
имеют одинаковую вероятность, поэтому наиболее
вероятная проекция и средняя проекция скорости равны
нулю 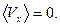
Обсудим вид полученной функции  , сравнив её с функцией распределения по абсолютным значениям скоростей.
, сравнив её с функцией распределения по абсолютным значениям скоростей.
Плотность фазовых точек, как при распределении по абсолютным скоростям, так и по проекциям скоростей, наибольшая в центре системы координат:

 .
.
В распределении по абсолютным значениям скорости элементарный
фазовый объем растет с увеличением абсолютного значения
скорости:
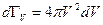 .
.
Поэтому, как мы уже отмечали, максимум функции распределения по
скоростям 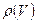 сдвигается относительно начала координат из-за более
сдвигается относительно начала координат из-за более
быстрого (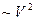 ) на начальном участке роста элементарного фазового
) на начальном участке роста элементарного фазового
 объема
объема  по сравнению с экспоненциальным спадом плотности
по сравнению с экспоненциальным спадом плотности
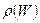 фазовых точек.
фазовых точек.
Функция распределения  , как следует из (3.4), не содержит
, как следует из (3.4), не содержит
квадратичного по скорости множителя, а элементарный фазовый объем 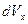
одинаков всюду вдоль оси 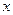 . Поэтому наибольшей будет вероятность
. Поэтому наибольшей будет вероятность
обнаружения молекулы в окрестности точки  , где плотность
, где плотность 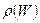
фазовых точек максимальна.
Качественная зависимость функции распределения  от температуры
от температуры 
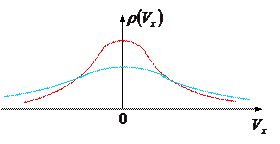 показана на следующем рисунке. Очевидно, что чем
показана на следующем рисунке. Очевидно, что чем
выше температура, тем положе становится кривая,
поскольку плотность фазовых точек в начале координат,
как это следует из (3.1), падает с температурой, а
площади под кривыми одинаковы и нормированы на
единицу, в чем легко убедиться. Это следует
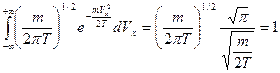 . (3.5)
. (3.5)
Для подсистемы, состоящей из 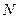 молекул, вероятность того, что рассматриваемая подсистема обладает кинетической энергией
молекул, вероятность того, что рассматриваемая подсистема обладает кинетической энергией 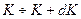 , находясь в определенном объеме фазового пространства
, находясь в определенном объеме фазового пространства  , равна
, равна
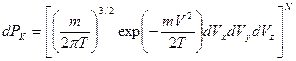 . (3.6)
. (3.6)
Это распределение справедливо для любой системы с произвольным взаимодействием между молекулами, подчиняющейся законам классической физики.
3.2. Средняя кинетическая энергия молекулы на одну поступательную степень свободы
Вычислим среднюю энергию, приходящуюся на одну степень свободы поступательного движения молекулы, т.е. сосчитаем 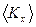 - долю кинетической энергии, относящуюся к движению по оси
- долю кинетической энергии, относящуюся к движению по оси 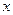 :
:
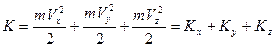 , (3.7)
, (3.7)
 (3.8)
(3.8)
Так как
 ,
,
получаем
 (3.9)
(3.9)
Итак, кинетическая энергия, приходящаяся на одну степень свободы, равна “половинке” 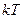 , причем
, причем
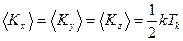 (3.10)
(3.10)
Тогда среднее значение кинетической энергии поступательного движения молекулы равно
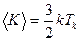 (3.11)
(3.11)
3.3. Число ударов молекул о единицу поверхности стенки в единицу времени (плотность потока частиц).
Пусть  концентрация молекул в интересующем нас объеме.
концентрация молекул в интересующем нас объеме.
Тогда концентрация молекул, имеющих скорости 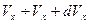
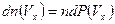 ,
,
а число молекул в выделенном объеме, имеющих скорости в интервале 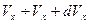
 .
.
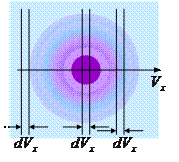
 Количество молекул, движущихся в положительном направлении оси
Количество молекул, движущихся в положительном направлении оси 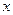 :
:

(подстановка:  ;
;  ;
; 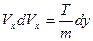 .)
.)
 .
.
Т.о., плотность потока частиц 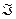 на стенку:
на стенку:
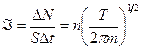 ,
,
или, учитывая, что  , получаем
, получаем
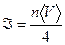 . (3.12)
. (3.12)
3.4. Давление, оказываемое термодинамически равновесным газом на стенку.
Выберем площадку  , нормаль к которой направлена против оси
, нормаль к которой направлена против оси 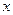 . Тогда давление газа
. Тогда давление газа
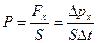 ;
;  , (см. рис.)
, (см. рис.)
интеграл
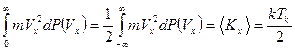 сосчитан в п. 3.2;
сосчитан в п. 3.2;
получаем
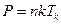 .
.
3.5. Вероятность найти частицу со скоростью, лежащей в заданном интервале
Воспользуемся распределением Максвелла в приведенном виде.
 , где
, где 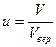 и
и 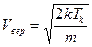 .
.
Приведенные в таблице данные позволяют сделать практически полезный вывод о том, что при вычислениях, проводимых для интервалов, превышающих  , можно интегрировать в пределах от
, можно интегрировать в пределах от  до
до 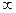 , сохраняя высокую точность вычислений.
, сохраняя высокую точность вычислений.



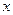 :
: 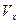 .
.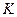 до
до 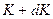 , обладая при этом определенными проекциями скоростей:
, обладая при этом определенными проекциями скоростей: ).
). на соответствующий фазовый объем
на соответствующий фазовый объем  :
: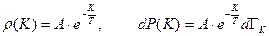 (3.1)
(3.1) и запишем её фазовый объем в пространстве скоростей:
и запишем её фазовый объем в пространстве скоростей:  .
. уже была определена в предыдущем параграфе из условия нормировки.
уже была определена в предыдущем параграфе из условия нормировки.
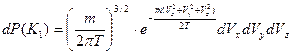 (3.2)
(3.2)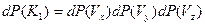 ,
,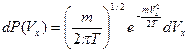 (3.3)
(3.3) ой проекции скорости:
ой проекции скорости: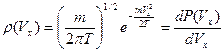 . (3.4)
. (3.4) координат и имеет максимум при проекции скорости
координат и имеет максимум при проекции скорости . Положительные и отрицательные значения
. Положительные и отрицательные значения 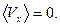
 , сравнив её с функцией распределения по абсолютным значениям скоростей.
, сравнив её с функцией распределения по абсолютным значениям скоростей.
 .
.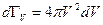 .
.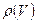 сдвигается относительно начала координат из-за более
сдвигается относительно начала координат из-за более 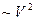 ) на начальном участке роста элементарного фазового
) на начальном участке роста элементарного фазового  объема
объема  по сравнению с экспоненциальным спадом плотности
по сравнению с экспоненциальным спадом плотности 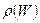 фазовых точек.
фазовых точек.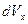

 показана на следующем рисунке. Очевидно, что чем
показана на следующем рисунке. Очевидно, что чем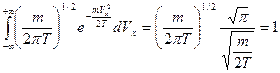 . (3.5)
. (3.5)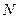 молекул, вероятность того, что рассматриваемая подсистема обладает кинетической энергией
молекул, вероятность того, что рассматриваемая подсистема обладает кинетической энергией 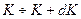 , находясь в определенном объеме фазового пространства
, находясь в определенном объеме фазового пространства 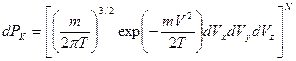 . (3.6)
. (3.6)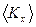 - долю кинетической энергии, относящуюся к движению по оси
- долю кинетической энергии, относящуюся к движению по оси 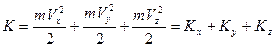 , (3.7)
, (3.7) (3.8)
(3.8) ,
, (3.9)
(3.9)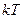 , причем
, причем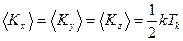 (3.10)
(3.10)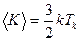 (3.11)
(3.11) концентрация молекул в интересующем нас объеме.
концентрация молекул в интересующем нас объеме.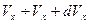
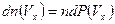 ,
, .
. Количество молекул, движущихся в положительном направлении оси
Количество молекул, движущихся в положительном направлении оси 
 ;
;  ;
; 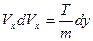 .)
.) .
.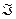 на стенку:
на стенку: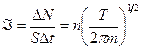 ,
, , получаем
, получаем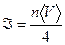 . (3.12)
. (3.12) , нормаль к которой направлена против оси
, нормаль к которой направлена против оси 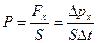 ;
;  , (см. рис.)
, (см. рис.)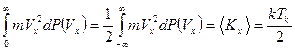 сосчитан в п. 3.2;
сосчитан в п. 3.2;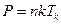 .
. , где
, где 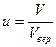 и
и 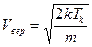 .
.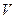



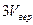
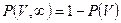

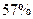
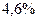

 до
до 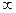 , сохраняя высокую точность вычислений.
, сохраняя высокую точность вычислений.

