Декремент. Числа Стирлинга первого рода.
Мы уже знаем, что количество всех перестановок порядка n равно  , а количество тех из них, которые не сохраняют на месте ни одно число, называется число беспорядков, или субфакториал, и равно
, а количество тех из них, которые не сохраняют на месте ни одно число, называется число беспорядков, или субфакториал, и равно 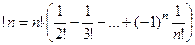 .
.
Иногда удобно рассматривать не перестановку, а именно подстановку, то есть биекцию n-элементного множества на себя.

 здесь
здесь  .
.
Если рассмотреть композицию  , то получится другая подстановка:
, то получится другая подстановка:
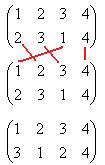
1 перешло в 2, затем 2 в 3, в итоге 1 в 3.
Куб этой подстановки 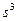 приведёт к тождественной.
приведёт к тождественной.
Бывает так, что при любой степени подстановки некоторое подмножество остаётся замкнутым относительно всех этих операций, то есть отображается только на само себя. В данном примере это два подмножества {1,2,3} и {4}. Они образуют независимые циклы.
 = (231)(4) краткая запись.
= (231)(4) краткая запись.
Другой пример:  = (21)(43)
= (21)(43)
Изучим, как меняется количество циклов при транспозиции элементов  , взятых из одного цикла или разных циклов.
, взятых из одного цикла или разных циклов.
1) Поменяем местами пару элементов, находящихся в одном и том же цикле, например 2 и 3. Стало  = (31)(2)(4).
= (31)(2)(4).
один цикл распался на два, стало 3 цикла.
2) Поменяем местами пару элементов, находящихся в разных циклах, например 2 и 4 в 
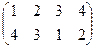 = (4231) стал один цикл, 2 цикла объединились.
= (4231) стал один цикл, 2 цикла объединились.
Декремент подстановки.
Пусть подстановка n-й степени разложена в произведение циклических подстановок. Пусть  — число циклических подстановок-сомножителей (в том числе циклов длины 1). Тогда декрементом называется разность
— число циклических подстановок-сомножителей (в том числе циклов длины 1). Тогда декрементом называется разность  .
.
В примере  = (231)(4),
= (231)(4), 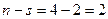 .
.
Сама перестановка чётная (инверсии только 2,1 и 3,1) и декремент тоже чётный.
Теорема. Декремент четен для четной подстановки и нечетен для нечетной подстановки.
Доказательство. Если изначально рассмотреть тождественную подстановку, то она содержит n циклов, каждый состоит из одного элемента. Она чётна, так как 0 инверсий. При этом  =
=  тоже чётно.
тоже чётно.
Мы можем перейти к искомой подстановке с помощью серии транспозиций. Первая из них (после тождественной) меняет 2 элемента, становится 1 цикл из двух элементов и  одноэлементных цикла, чётность подстановки сменилась, и чётность декремента тоже, так как
одноэлементных цикла, чётность подстановки сменилась, и чётность декремента тоже, так как  . Далее каждый раз при транспозиции меняется чётность, а один цикл либо появляется, либо исчезает (в зависимости от того, меняем мы элементы из одного цикла или из разных), то есть чётность декремента тоже меняется при каждой транспозиции синхронно с чётностью подстановки.
. Далее каждый раз при транспозиции меняется чётность, а один цикл либо появляется, либо исчезает (в зависимости от того, меняем мы элементы из одного цикла или из разных), то есть чётность декремента тоже меняется при каждой транспозиции синхронно с чётностью подстановки.
Для больших n легче разложить в произведение циклов и найти декремент, чем все инверсии (n действий по сравнению (n^2 – n)/2).
Пример.
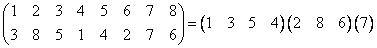
равен  , так как здесь 3 цикла. Подстановка нечетна (все инверсии искать не требуется, чтобы утверждать это).
, так как здесь 3 цикла. Подстановка нечетна (все инверсии искать не требуется, чтобы утверждать это).
Числа Стирлинга первого рода (без знака) — количество перестановок порядка n с k циклами. Обозначается 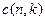 .
.
n=2
2 цикла - одна перестановка: (12)
1 цикл - одна перестановка: (21)
n=3
3 цикла - одна перестановка: (123)
2 цикла - 3 перестановки: (213) (321) (132)
1 цикл - 2 перестановки: (231) (312)
По крайней мере, начало таблицы чисел Стирлинга 1 рода мы можем составить:

Точно известно, что перестановок порядка n с n циклами всего одна, и она тождественная.
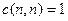
Отличие от чисел Стирлинга 2 рода: там рассматриваются только подмножества, а здесь, разбив n-элементное множество на подмножества, внутри каждого ещё можно по-разному переставить элементы, то есть для каждого подмножества ещё может быть несколько подстановок, поэтому числа Стирлинга 1 рода больше или равны, чем соответствующие числа Стирлинга 2 рода..
 .
.
Сначала изучим, сколько может быть перестановок с одним циклом.
Их количество  . Докажем этот факт.
. Докажем этот факт.
Пусть 1 переходит в какое-то число  , должно быть в одно из
, должно быть в одно из 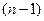 оставшихся, но не в 1 (иначе уже был бы отдельный цикл только из одного элемента, а значит, количество циклов было бы
оставшихся, но не в 1 (иначе уже был бы отдельный цикл только из одного элемента, а значит, количество циклов было бы  ).
).
 отображается в
отображается в  , где
, где  любое из
любое из 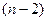 оставшихся кроме 1 и
оставшихся кроме 1 и  .
.
Если было бы  и
и  , то был бы отдельный 2-элементный цикл, а значит снова единый цикл из n элементов не получился бы.
, то был бы отдельный 2-элементный цикл, а значит снова единый цикл из n элементов не получился бы.
 вообще исключено, так как
вообще исключено, так как  , а в подстановке во 2 строке не могут быть два одинаковых числа, ведь подстановка это биекция.
, а в подстановке во 2 строке не могут быть два одинаковых числа, ведь подстановка это биекция.
Таким образом, вариантов уже  . Далее
. Далее  должно отобразиться в одно из
должно отобразиться в одно из 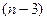 оставшихся элементов, и.т.д до последнего, где останется только 1 вариант.
оставшихся элементов, и.т.д до последнего, где останется только 1 вариант.  на последнем шаге, иначе цикл завершится раньше, и будет не 1 а больше циклов.
на последнем шаге, иначе цикл завершится раньше, и будет не 1 а больше циклов.
((21)(43) является беспорядком, но не одним циклом).
Число подстановок с одним циклом:
 =
= 
Мы уже посчитали следующие числа Стирлинга 1 рода:

ЛЕКЦИЯ 7. 4.3.2021
Теперь нам снова нужно вывести какую-то рекуррентную формулу, с помощью которой числа Стирлинга можно найти с помощью предыдущих и заполнить всю таблицу до любых требуемых  .
.
Верна следующая рекуррентная формула:
Доказательство. Рассмотрим все случаи, как в перестановке из  чисел могут образоваться
чисел могут образоваться 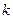 циклов.
циклов.
1) Если в перестановке из чисел  было
было 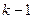 циклов, а новое число
циклов, а новое число  на последнем месте, то оно образует
на последнем месте, то оно образует 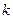 -й цикл.
-й цикл.
Число таких вариантов  .
.
2) Если в перестановке из  чисел было
чисел было 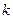 циклов, число
циклов, число  на последнем месте образовало бы
на последнем месте образовало бы 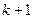 -й цикл, если его затем поменять с любым меньшим числом, которых имеется
-й цикл, если его затем поменять с любым меньшим числом, которых имеется  , то два цикла объединятся и их количество станет
, то два цикла объединятся и их количество станет 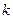 . Число таких вариантов
. Число таких вариантов 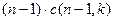 .
.
3) Если в исходной подстановке порядка  было
было  и менее, либо
и менее, либо 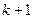 и более циклов. В этом случае тоже можно привести к
и более циклов. В этом случае тоже можно привести к 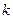 , но уже с помощью серии из нескольких транспозиций, где число
, но уже с помощью серии из нескольких транспозиций, где число  будет переставлено несколько раз. Однако эти случаи учитывать не надо, так как они уже учтены: ведь если
будет переставлено несколько раз. Однако эти случаи учитывать не надо, так как они уже учтены: ведь если  попадает на какое-то место
попадает на какое-то место  , то можно было заранее осуществить некоторые транспозиции в исходной перестановке, чтобы потом
, то можно было заранее осуществить некоторые транспозиции в исходной перестановке, чтобы потом  поменять с чем-то только 1 раз. А такие перестановки все уже учтены.
поменять с чем-то только 1 раз. А такие перестановки все уже учтены.
Итак,  .
.
В отличие от чисел Стирлинга 2 рода, где было

здесь надо элемент слева и сверху по диагонали, прибавить к тому, который ровно над искомой клеткой, но умножать его не на номер столбца, а на номер строки (той, которая выше).
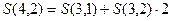 ,
, 
 ,
, 
Начало таблицы для чисел Стирлинга 2 и 1 рода:
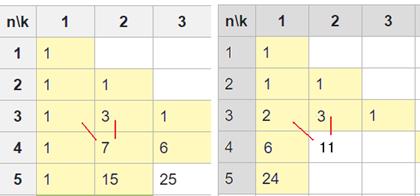
Ниже 11 будет число  .
.
С помощью рекурсии можно найти и все остальные числа.
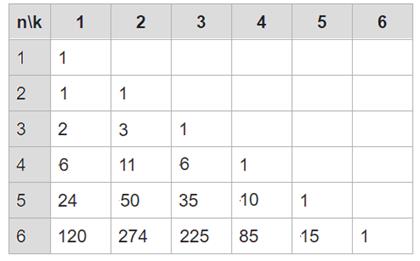
В каждой строке получается число всех перестановок порядка  , то есть
, то есть  , и эти числа больше или равны, чем числа Белла (равны лишь при
, и эти числа больше или равны, чем числа Белла (равны лишь при  и
и 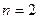 ). Там была последовательность: 1, 2, 5, 15, 52,...
). Там была последовательность: 1, 2, 5, 15, 52,...
а здесь 1, 2, 6, 24, 120,...



 , а количество тех из них, которые не сохраняют на месте ни одно число, называется число беспорядков, или субфакториал, и равно
, а количество тех из них, которые не сохраняют на месте ни одно число, называется число беспорядков, или субфакториал, и равно 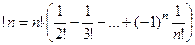 .
.
 здесь
здесь  .
.  , то получится другая подстановка:
, то получится другая подстановка:
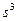 приведёт к тождественной.
приведёт к тождественной. = (21)(43)
= (21)(43) , взятых из одного цикла или разных циклов.
, взятых из одного цикла или разных циклов.  = (31)(2)(4).
= (31)(2)(4).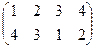 = (4231) стал один цикл, 2 цикла объединились.
= (4231) стал один цикл, 2 цикла объединились. — число циклических подстановок-сомножителей (в том числе циклов длины 1). Тогда декрементом называется разность
— число циклических подстановок-сомножителей (в том числе циклов длины 1). Тогда декрементом называется разность  .
.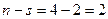 .
.  тоже чётно.
тоже чётно.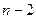 одноэлементных цикла, чётность подстановки сменилась, и чётность декремента тоже, так как
одноэлементных цикла, чётность подстановки сменилась, и чётность декремента тоже, так как  . Далее каждый раз при транспозиции меняется чётность, а один цикл либо появляется, либо исчезает (в зависимости от того, меняем мы элементы из одного цикла или из разных), то есть чётность декремента тоже меняется при каждой транспозиции синхронно с чётностью подстановки.
. Далее каждый раз при транспозиции меняется чётность, а один цикл либо появляется, либо исчезает (в зависимости от того, меняем мы элементы из одного цикла или из разных), то есть чётность декремента тоже меняется при каждой транспозиции синхронно с чётностью подстановки. 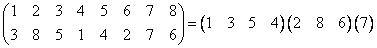
 , так как здесь 3 цикла. Подстановка нечетна (все инверсии искать не требуется, чтобы утверждать это).
, так как здесь 3 цикла. Подстановка нечетна (все инверсии искать не требуется, чтобы утверждать это).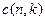 .
.
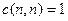
 .
. . Докажем этот факт.
. Докажем этот факт. , должно быть в одно из
, должно быть в одно из 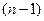 оставшихся, но не в 1 (иначе уже был бы отдельный цикл только из одного элемента, а значит, количество циклов было бы
оставшихся, но не в 1 (иначе уже был бы отдельный цикл только из одного элемента, а значит, количество циклов было бы  ).
). , где
, где 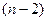 оставшихся кроме 1 и
оставшихся кроме 1 и  и
и  , то был бы отдельный 2-элементный цикл, а значит снова единый цикл из n элементов не получился бы.
, то был бы отдельный 2-элементный цикл, а значит снова единый цикл из n элементов не получился бы. вообще исключено, так как
вообще исключено, так как  . Далее
. Далее 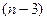 оставшихся элементов, и.т.д до последнего, где останется только 1 вариант.
оставшихся элементов, и.т.д до последнего, где останется только 1 вариант.  на последнем шаге, иначе цикл завершится раньше, и будет не 1 а больше циклов.
на последнем шаге, иначе цикл завершится раньше, и будет не 1 а больше циклов. =
= 
 .
.
 чисел могут образоваться
чисел могут образоваться 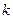 циклов.
циклов. было
было 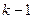 циклов, а новое число
циклов, а новое число  .
. чисел было
чисел было 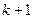 -й цикл, если его затем поменять с любым меньшим числом, которых имеется
-й цикл, если его затем поменять с любым меньшим числом, которых имеется 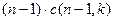 .
. и менее, либо
и менее, либо  , то можно было заранее осуществить некоторые транспозиции в исходной перестановке, чтобы потом
, то можно было заранее осуществить некоторые транспозиции в исходной перестановке, чтобы потом 
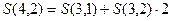 ,
, 
 ,
, 

 .
. 
 и
и 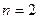 ). Там была последовательность: 1, 2, 5, 15, 52,...
). Там была последовательность: 1, 2, 5, 15, 52,... 

