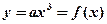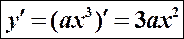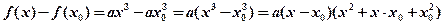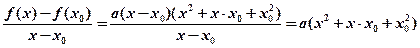Лекция
Тема: Производная. Понятие о производной функции, её геометрический и физический смысл. Уравнение касательной к графику функции.
При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов. Ее решение приводит к понятию производной, являющемуся основным понятием дифференциального исчисления.
Метод дифференциального исчисления был создан в XVII и XVIII вв. С возникновением этого метода связаны имена двух великих математиков – И.Ньютона и Г.Лейбница.
Механическое истолкование производной было впервые дано И.Ньютоном. Оно заключается в следующем: скорость движения материальной точки в данный момент времени равна производной пути по времени.
Лейбниц пришел к открытию дифференциального исчисления при решении задачи о построении касательной к любой кривой, заданной уравнением.
Решение этой задачи имеет большое значение. Ведь скорость движущейся точки направлена по касательной к ее траектории, поэтому определение скорости снаряда на его траектории, скорости любой планеты на ее орбите сводится к определению направления касательной к кривой.
Введём понятие производной.
Пусть  – некоторая функция, определенная на промежутке (a; b) и
– некоторая функция, определенная на промежутке (a; b) и  - некоторая фиксированная точка этого промежутка. Возьмем произвольное значение x из промежутка (a; b) и составим разность x -
- некоторая фиксированная точка этого промежутка. Возьмем произвольное значение x из промежутка (a; b) и составим разность x -  . Разность x -
. Разность x -  называют приращением независимой переменной (или приращением аргумента) функции
называют приращением независимой переменной (или приращением аргумента) функции  в точке
в точке  и обозначают
и обозначают 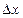 :
:
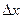 = x -
= x -  (1)
(1)
Приращением функции  в точке
в точке  называют разность между значением функции в точке
называют разность между значением функции в точке 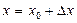 и значением функции в точке
и значением функции в точке  и обозначают
и обозначают 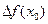 :
:
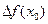 =
= 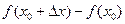 (2).
(2).
Т.к. точка  считается фиксированной, приращением функции
считается фиксированной, приращением функции 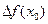 является функцией приращения аргумента
является функцией приращения аргумента 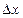 .
.
Составим отношение
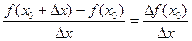 ,
,
которое также будет функцией приращения аргумента 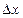 ; и рассмотрим предел этого выражения при
; и рассмотрим предел этого выражения при 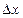 , стремящемся к нулю:
, стремящемся к нулю:
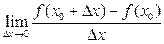 .
.
Если этот предел существует, то говорят, что функция  имеет производную в точке
имеет производную в точке  , и пишут:
, и пишут:
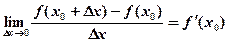 (3).
(3).
Число 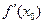 называется производной функции в точке
называется производной функции в точке  .
.
Нахождение производной называется дифференцированием функции.
Если существует предел (3), также говорят, что функция  дифференцируема в точке
дифференцируема в точке  .
.
Если функция  дифференцируема в каждой точке промежутка (a; b), то говорят, что она дифференцируема в промежутке (a; b).
дифференцируема в каждой точке промежутка (a; b), то говорят, что она дифференцируема в промежутке (a; b).
Производная функции  , дифференцируемой в промежутке (a; b), сама является функцией x.
, дифференцируемой в промежутке (a; b), сама является функцией x.
Правило нахождения производной
Чтобы вычислить производную функции  в точке
в точке  нужно:
нужно:
1. найти разность  .
.
2. найти отношение 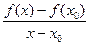 .
.
3. найти предел этого отношения при 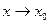 :
: 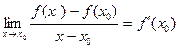
Производная – это «новая» функция, произведенная от данной функции по указанному правилу.
Определим производные следующих функций:
а) линейной функции 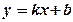
б) квадратичной функции 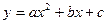
в) кубической функции 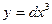
Решение:
а) 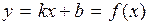

т.к.
1. 
2. 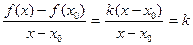
3.  .
.
б) 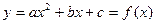
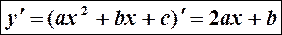
т.к.
1. 
2. 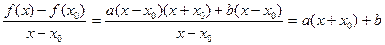
3. 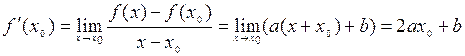 .
.
в) 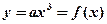
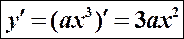
т.к.
1. 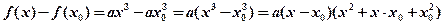
2. 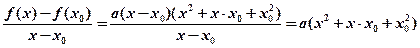
3. 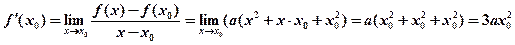
Контрольные вопросы:
Лекция
Тема: Производная. Понятие о производной функции, её геометрический и физический смысл. Уравнение касательной к графику функции.
При изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов. Ее решение приводит к понятию производной, являющемуся основным понятием дифференциального исчисления.
Метод дифференциального исчисления был создан в XVII и XVIII вв. С возникновением этого метода связаны имена двух великих математиков – И.Ньютона и Г.Лейбница.
Механическое истолкование производной было впервые дано И.Ньютоном. Оно заключается в следующем: скорость движения материальной точки в данный момент времени равна производной пути по времени.
Лейбниц пришел к открытию дифференциального исчисления при решении задачи о построении касательной к любой кривой, заданной уравнением.
Решение этой задачи имеет большое значение. Ведь скорость движущейся точки направлена по касательной к ее траектории, поэтому определение скорости снаряда на его траектории, скорости любой планеты на ее орбите сводится к определению направления касательной к кривой.
Введём понятие производной.
Пусть  – некоторая функция, определенная на промежутке (a; b) и
– некоторая функция, определенная на промежутке (a; b) и  - некоторая фиксированная точка этого промежутка. Возьмем произвольное значение x из промежутка (a; b) и составим разность x -
- некоторая фиксированная точка этого промежутка. Возьмем произвольное значение x из промежутка (a; b) и составим разность x -  . Разность x -
. Разность x -  называют приращением независимой переменной (или приращением аргумента) функции
называют приращением независимой переменной (или приращением аргумента) функции  в точке
в точке  и обозначают
и обозначают 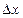 :
:
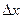 = x -
= x -  (1)
(1)
Приращением функции  в точке
в точке  называют разность между значением функции в точке
называют разность между значением функции в точке 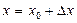 и значением функции в точке
и значением функции в точке  и обозначают
и обозначают 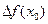 :
:
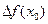 =
= 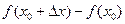 (2).
(2).
Т.к. точка  считается фиксированной, приращением функции
считается фиксированной, приращением функции 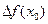 является функцией приращения аргумента
является функцией приращения аргумента 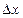 .
.
Составим отношение
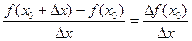 ,
,
которое также будет функцией приращения аргумента 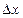 ; и рассмотрим предел этого выражения при
; и рассмотрим предел этого выражения при 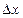 , стремящемся к нулю:
, стремящемся к нулю:
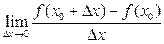 .
.
Если этот предел существует, то говорят, что функция  имеет производную в точке
имеет производную в точке  , и пишут:
, и пишут:
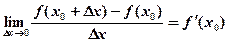 (3).
(3).
Число 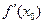 называется производной функции в точке
называется производной функции в точке  .
.



 – некоторая функция, определенная на промежутке (a; b) и
– некоторая функция, определенная на промежутке (a; b) и  - некоторая фиксированная точка этого промежутка. Возьмем произвольное значение x из промежутка (a; b) и составим разность x -
- некоторая фиксированная точка этого промежутка. Возьмем произвольное значение x из промежутка (a; b) и составим разность x - 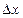 :
: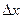 = x -
= x - 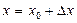 и значением функции в точке
и значением функции в точке 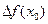 :
: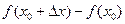 (2).
(2).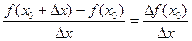 ,
,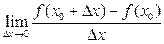 .
. 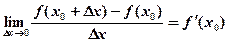 (3).
(3).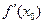 называется производной функции в точке
называется производной функции в точке  .
.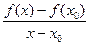 .
.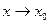 :
: 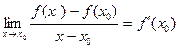
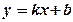
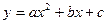
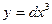
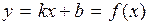


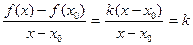
 .
.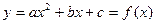
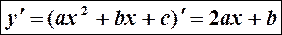

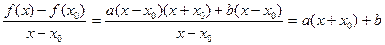
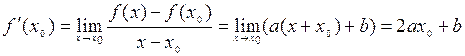 .
.