Пусть  – три произвольных вектора.
– три произвольных вектора.
Три вектора называются компланарными, если они параллельны одной плоскости, т.е., будучи приведены к одному началу, лежат в одной плоскости.
Смешанным произведением векторов  называется число равное скалярному произведению векторного произведения векторов
называется число равное скалярному произведению векторного произведения векторов 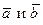 на вектор
на вектор 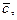 т.е.
т.е.  Геометрический смысл смешанного произведения определяется следующей теоремой.
Геометрический смысл смешанного произведения определяется следующей теоремой.
Теорема 2.1. Смешанное произведение  равно объему параллелепипеда V, построенного на векторах
равно объему параллелепипеда V, построенного на векторах  , взятому со знаком "+", если тройка векторов
, взятому со знаком "+", если тройка векторов  правая, и со знаком "–", если тройка векторов
правая, и со знаком "–", если тройка векторов  левая.
левая.
Если векторы  компланарны, то смешанное произведение рано нулю, т.е.
компланарны, то смешанное произведение рано нулю, т.е.
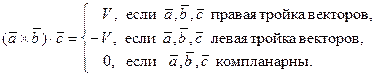
Теорема 2.2. В смешанном произведении векторов знаки векторного и скалярного произведений можно поменять местами, т.е.
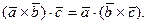
Так как справедлива теорема 2.2, смешанное произведение обозначают символом 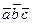 .
.
Найдем выражение смешанного произведения векторов через координаты сомножителей. Пусть

тогда по формулам (2.9), (2.11) находим:
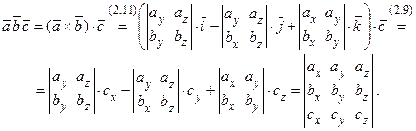
Основные приложения смешанного произведения векторов
1. Вычисление объема тетраэдра и параллелепипеда, построенного на векторах  (рис. 2.10).
(рис. 2.10).
Если векторы  некомпланарны, то по теореме 2.1
некомпланарны, то по теореме 2.1
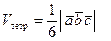 - объем тэтраэдра. (2.13)
- объем тэтраэдра. (2.13)
 объем параллепипеда.
объем параллепипеда.
2. Вычисление высоты тетраэдра (параллелепипеда).
Вычислим объем тетраэдра двумя способами:
с одной стороны,
 ,
,
с другой стороны,
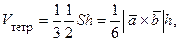
отсюда 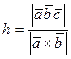 (высота параллелепипеда такая же);
(высота параллелепипеда такая же);
3. Условие компланарности векторов (теорема 2.1):
 – компланарны.
– компланарны.
Задание на Дом:
РЕШИТЬ ЗАДАЧИ
Тема 1. Векторная алгебра.
1.Даны векторы  (2;1) и (2;1) и 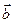 (-1;1). Найти скалярное произведение (-1;1). Найти скалярное произведение 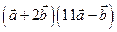 2.Даны векторы
2.Даны векторы 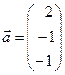 и и 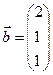 .
Найти скалярное произведение .
Найти скалярное произведение 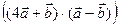 3.Даны векторы
3.Даны векторы  (1;1) и (1;1) и 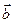 (-5;2). Найти скалярное произведение (-5;2). Найти скалярное произведение 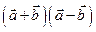
|
4.Определить площадь треугольника, построенного на векторах 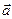 =(3;2;0), =(3;2;0),  =(0;-1;1). =(0;-1;1).
|
5.Определить площадь треугольника, построенного на векторах 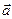 =(1;2;0), =(1;2;0),  =(2;-1;3). =(2;-1;3).
|
6.Определить объём параллелепипеда, построенного на векторах 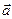 =(-1;1;0), =(-1;1;0),  =(3;1;1), =(3;1;1), 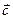 =(0;-1;-2). =(0;-1;-2).
|
Тема 2. Матрицы и определители.
П.2.1. Понятие матрицы
Опр. 1. Прямоугольная таблица чисел, состоящая из m строк и n столбцов, называется матрицей.
Для обозначения матриц используются прописные буквы латинского алфавита: А, В, С,....
Числа, образующие матрицу, называются ее элементами. В обозначениях элементы матрицы, снабжаются двумя индексами i, j, первый индекс – номер строки, второй индекс – номер столбца, в которых находится элемент, т.е. 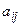 (i = 1, 2,..., m; j = 1, 2,..., n) элементы матрицы. Таким образом, полное обозначение матрицы имеет вид:
(i = 1, 2,..., m; j = 1, 2,..., n) элементы матрицы. Таким образом, полное обозначение матрицы имеет вид:
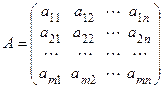 . (2.1)
. (2.1)
Для краткого обозначения матрицы будем использовать запись:
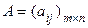 (2.2)
(2.2)
Числа m и n называются размерами матрицы, т.е. (2.1), (2.2) – записи матрицы размеров m на n (m строк и n столбцов).
Опр. 2. Если число строк матрицы совпадает с числом столбцов, т.е. m = n, то матрица называется квадратной порядка n.
Опр. 3. Матрица, в которой столбцы заменены строками, а строки столбцами, называется транспонированной и обозначается 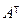 .
.
Опр. 4. Элементы квадратной матрицы с одинаковыми индексами называются главной диагональю, т.е. элементами главной диагонали будут: 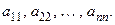
Транспонированная матрица 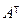 получается из матрицы А поворотом на 180° относительно главной диагонали. Например,
получается из матрицы А поворотом на 180° относительно главной диагонали. Например,
если 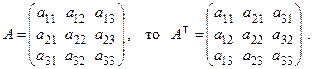
Действия над матрицами
Рассмотрим две матрицы одинаковых размеров m  n:
n: 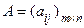 ,
, 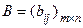 . Обозначим через I множество, состоящее из первых m чисел натурального ряда, т.е.
. Обозначим через I множество, состоящее из первых m чисел натурального ряда, т.е.
I = {1, 2,..., m}.
1. Опр.5 Матрицы А и В называются равными, если
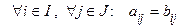 ,
,
т.e. в которых равны элементы, стоящие на одинаковых местах.
Обозначается: А = В.
2. Опр. 6. Суммой матриц А и В называется матрица 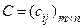 , элементы которой определяются по формулам:
, элементы которой определяются по формулам:
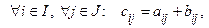
т.e. элементы матрицы С равнысумме соответствующих элементов матриц А и В.
Обозначается: С = А + В.
3. Опр. 7.Произведением матрицы А на действительное число 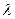 называется матрица
называется матрица 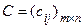 , элементы которой вычисляются по формуле:
, элементы которой вычисляются по формуле:
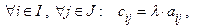
т.е. каждый элемент матрицы А умножается на число 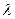 .
.
Обозначается: 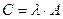 .
.
Пусть теперь 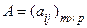 ,
, 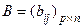 , т.е. число столбцов матрицы А совпадает с числом строк матрицы В.
, т.е. число столбцов матрицы А совпадает с числом строк матрицы В.
4. Опр8. Произведением матрицы А на матрицу В называется матрица размера m 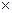 n
n 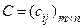 , элементы которой вычисляются по формуле:
, элементы которой вычисляются по формуле:
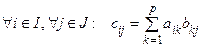 ,
,
т.е. элемент матрицы С с номерами i и j равен сумме попарных произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В (правило «строка на столбец»). Обозначается: 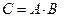 .
.
Например, если 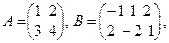 то элементы матрицы
то элементы матрицы 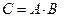 будут равны:
будут равны:
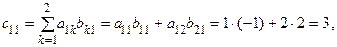
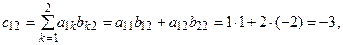
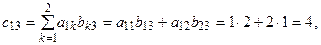
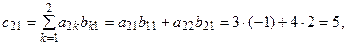
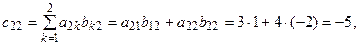
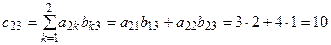 ,
,
таким образом
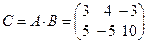 .
.
Произведение матриц не коммутативно (не перестановочно)!, т.е., вообще говоря, 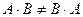 .
.
Опр. 9. если все-таки 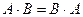 , то матрицы А и В называются перестановочными.
, то матрицы А и В называются перестановочными.
Опр.10. Квадратная матрица, у которой элементы, стоящие на главной диагонали равны 1, а все остальные равны 0, называется единичной и обозначается: Е.
Единичная матрица перестановочна с любой квадратной матрицей порядка n, так как нетрудно убедиться, что 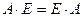 .
.
Опр.11. Определим понятие обратной матрицы. Оно определяется только для квадратных матриц. Далее А – квадратная матрица порядка n.
Матрица 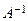 называется обратной к матрице А, если
называется обратной к матрице А, если
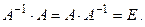
Поэтому матрицы А и 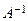 называются взаимно обратными.
называются взаимно обратными.
П.2.2. Определители.
Рассмотрим квадратную матрицу 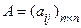 порядка n.
порядка n.
Опр. 12. Определителем или детерминантом n-го порядка матрицы А называется число 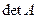
где сумма вычисляется по всем перестановкам вторых индексов. 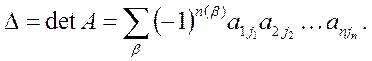 (2.3)
(2.3)
Обозначения определителя: 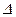 , det A, или в полной записи:
, det A, или в полной записи:
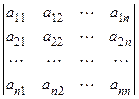 .
.
Используя определение определителя порядка n, получим формулы для вычисления определителей 2-го и 3-го порядка.
При n =2:
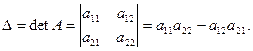 (2.4)
(2.4)
При n = 3.
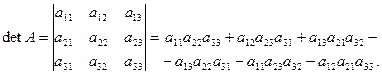 (2.5)
(2.5)



 – три произвольных вектора.
– три произвольных вектора.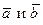 на вектор
на вектор 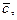 т.е.
т.е.  Геометрический смысл смешанного произведения определяется следующей теоремой.
Геометрический смысл смешанного произведения определяется следующей теоремой. компланарны, то смешанное произведение рано нулю, т.е.
компланарны, то смешанное произведение рано нулю, т.е.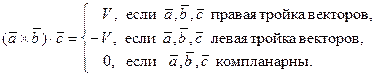
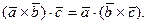
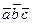 .
.
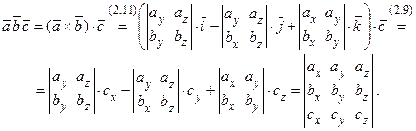
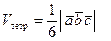 - объем тэтраэдра. (2.13)
- объем тэтраэдра. (2.13) объем параллепипеда.
объем параллепипеда. ,
,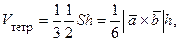
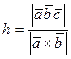 (высота параллелепипеда такая же);
(высота параллелепипеда такая же); – компланарны.
– компланарны. (2;1) и
(2;1) и 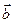 (-1;1). Найти скалярное произведение
(-1;1). Найти скалярное произведение 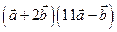 2.Даны векторы
2.Даны векторы 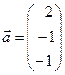 и
и 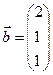 .
Найти скалярное произведение
.
Найти скалярное произведение 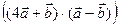 3.Даны векторы
3.Даны векторы 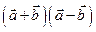
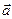 =(3;2;0),
=(3;2;0),  =(0;-1;1).
=(0;-1;1).
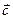 =(0;-1;-2).
=(0;-1;-2).
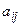 (i = 1, 2,..., m; j = 1, 2,..., n) элементы матрицы. Таким образом, полное обозначение матрицы имеет вид:
(i = 1, 2,..., m; j = 1, 2,..., n) элементы матрицы. Таким образом, полное обозначение матрицы имеет вид: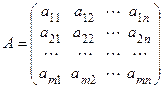 . (2.1)
. (2.1)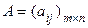 (2.2)
(2.2)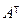 .
.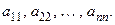
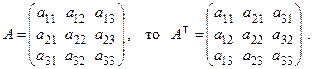
 n:
n: 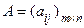 ,
, 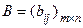 . Обозначим через I множество, состоящее из первых m чисел натурального ряда, т.е.
. Обозначим через I множество, состоящее из первых m чисел натурального ряда, т.е.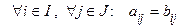 ,
,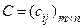 , элементы которой определяются по формулам:
, элементы которой определяются по формулам: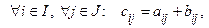
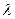 называется матрица
называется матрица 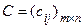 , элементы которой вычисляются по формуле:
, элементы которой вычисляются по формуле: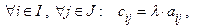
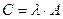 .
.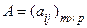 ,
, 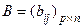 , т.е. число столбцов матрицы А совпадает с числом строк матрицы В.
, т.е. число столбцов матрицы А совпадает с числом строк матрицы В.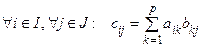 ,
,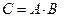 .
.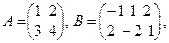 то элементы матрицы
то элементы матрицы 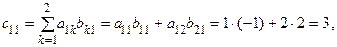
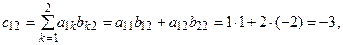
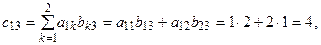
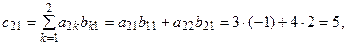
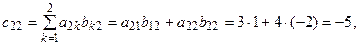
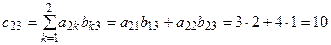 ,
,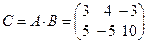 .
.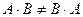 .
.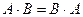 , то матрицы А и В называются перестановочными.
, то матрицы А и В называются перестановочными.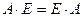 .
.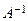 называется обратной к матрице А, если
называется обратной к матрице А, если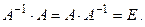
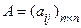 порядка n.
порядка n.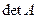
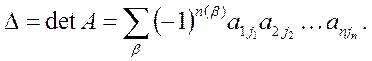 (2.3)
(2.3)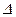 , det A, или в полной записи:
, det A, или в полной записи: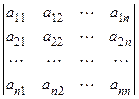 .
.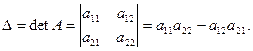 (2.4)
(2.4)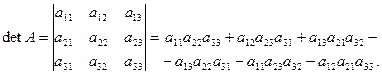 (2.5)
(2.5)


