Практическое занятие № 6
Теоретические сведения
Предварительная обработка данных. Для того чтобы оценить воспроизводимость анализа и провести статистическую обработку, необходимо прежде всего получить по одной и той же методике n результатов прямых измерений. Ими могут быть объемы титранта для нескольких одинаковых аликвот, значения аналитического сигнала при его повторных измерениях и т.п. Соответствующие величины (варианты выборки) должны относиться к одному и тому же объекту исследования и быть записаны в порядке их получения. В записи каждой варианты последняя значащая цифра должна соответствовать по разряду абсолютной погрешности измерения, в частности цене деления, а все варианты должны быть равноточными.
Статистическую обработку выборки нельзя вести при наличии грубых промахов, поэтому их надо заранее выявить и исключить. Из нескольких методов их выявления рекомендуется пользоваться наиболее простым - проверкой данных с помощью Q-теста (приложение 8). Если переписать варианты в порядке увеличения измеряемой величины (провести ранжирование), то грубыми промахами могут оказаться крайние варианты, т.е. наибольший или наименьший результаты. Для проверки сомнительного X1 (наименьшего результата) рассчитывают Qэксп по формуле:
Qэксп = 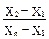 , (32)
, (32)
а при проверке сомнительного Xn (наибольшего результата) пользуются формулой:
Qэксп = 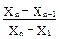 , (32а)
, (32а)
где xn и x1 - крайние варианты в ранжированной выборке,а x2 и xn-1 - ближайшие к ним.В любом случае величина Qэксп должна быть положительной. Сомнительная варианта (х1 или xn) отбрасывается, если значение Qэксп оказывается больше, чем Qтабл для выбранного уровня значимости и данного числа вариант (см. пример 1), в противном случае считают, что промах не выявлен, и сомнительный результат оставляют. Вместо Q-теста можно использовать более строгие критерии отбраковки грубых промахов. Так, при одновременном присутствии двух сомнительных результатов рекомендуется пользоваться методом максимальных относительных отклонений (пример 2).
Статистическая обработка не проводится и при наличии дрейфа - особого вида систематической погрешности данных, обычно связанной с изменением состава исследуемой пробы или реагентов во времени. Наличие дрейфа можно предположить, если при достаточно большом количестве вариант (не менее пяти) каждая из них последовательно оказывается больше (или меньше) предыдущей. В этом случае после отбраковки грубых промахов следует провести статистическую проверку значимости дрейфа. В выборке выделяют две группы вариант, взяв их в начале и в конце серии измерений. Затем сравнивают средние значения по обеим группам, пользуясь t-критерием (см. пример 7). Величину tтабл выбирают с учетом числа вариант в каждой из групп и требуемой достоверности выводов. Если tэксп > tтабл, считают дрейф доказанным. Никакая статистическая обработка полученных данных в этом случае не производится, а исследуются и устраняются причины дрейфа.
Проверка характера распределения. Наиболее распространенные способы статистической обработки результатов анализа основаны на предположении, что эти результаты подчиняются нормальному распределению, и вероятность получения любого возможного результата в их генеральной совокупности можно рассчитать по формулам Гаусса. Однако это предположение далеко не всегда истинно; для некоторых объектов и некоторых методик анализа результаты могут соответствовать распределению Пуассона или другим известным распределениям, отличающимся от нормального. Поэтому при достаточном объеме экспериментальных данных следует проверить характер их распределения. Для этого существует ряд способов [19-23], из которых наиболее простым является проверка значимости коэффициентов асимметрии и эксцесса (пример 3). Громоздкие расчеты этих коэффициентов удобно вести с применением специальных компьютерных программ. Если эти коэффициенты не превышают некоторых критических (табличных) значений, считают распределение симметричным и не имеющим достоверного эксцесса, что подтверждает предположение о нормальном (гауссовском) распределении результатов анализа. Возможны и более надежные способы (по критерию Пирсона), но они требуют еще большего объема вычислений.
Расчет выборочных параметров и доверительных интервалов. Если в описании используемой методики измерений (паспорте прибора, ГОСТе) не указываются количественные характеристики воспроизводимости - генеральное стандартное отклонение s или заменяющие его величины sr, sx сред и др., то доверительный интервал, в который с заданной надежностью попадает истинное значение измеряемой величины, находят по экспериментальным данным. Для этого после отбраковки грубых промахов рассчитывают следующие параметры:
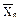 - среднее арифметическое из всех n вариант,
- среднее арифметическое из всех n вариант,
S2 - выборочную дисперсию;
S - выборочное стандартное отклонение
S 2 = 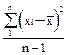 ; S =
; S = 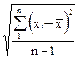 . (33)
. (33)
По выборочным параметрам можно с заданной надежностью оценить m - истинное значение измеряемой величины. Однако статистическая обработка не позволяет найти m, как и другие параметры генеральной совокупности, абсолютно точно. Мы находим лишь интервал значений, в котором с заданной вероятностью (надежностью) находится m. Ширина интервала при прочих равных условиях тем больше, чем больше эта вероятность, которая обозначается символом P. При расчете доверительных интервалов обычно используются значения P = 0,90; 0,95; 0,99.
Способ расчета доверительного интервала зависит от того, какому распределению случайных величин соответствуют полученные нами данные. В случае нормального распределения данных границы доверительного интервала Xmin и Xmax рассчитывают по формулам Стьюдента:
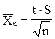 £ m £
£ m £ 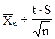 (34)
(34)
Расчеты по этой формуле дают правильные результаты только в том случае, когда исходные данные (результаты измерений) не содержат значимой систематической погрешности (примеры 4-5). Значения коэффициента Стьюдента (t) приведены в приложении 8. Вероятность того, что в отсутствие дрейфа, грубых промахов, систематических погрешностей и при нормальном распределении данных значение m случайно окажется вне границ доверительного интервала, равна 1 - P. Эту вероятность обозначают обычно буквой a и называют уровнем значимости. В справочниках значения коэффициента Стьюдента обычно приводятся для a = 0,10; 0,05 и 0,01.
Величина t зависит и от n (числа параллельно полученных результатов, используемых при расчете интервала). Однако в справочниках значения t приводятся как функция от числа степеней cвободы (df). При расчете доверительных интервалов df = n-1, в других случаях зависимость между n и df может быть иной[8].
Формулу (34) можно использовать не только для обработки прямых измерений, но и для обработки результатов анализа, вычисленных по прямым измерениям. Так, например, при титровании по методу отдельных навесок прямыми измерениями в каждом опыте являются значения массы и объема титранта, по ним вычисляют содержание компонента, но статистически обрабатывать ни эти объемы, ни массы нельзя. Доверительные интервалы рассчитывают для содержаний (массовых долей), вычисленных по результатам прямых измерений в параллельных опытах.
Выявление систематических ошибок. Несовпадение среднего результата анализа и истинного содержания компонента в исследуемом материале может быть случайностью, а может быть и следствием систематической погрешности анализа. Для проверки результаты многократного анализа образца с известным содержанием данного компонента выражают в виде доверительного интервала. Если истинное значение m в вычисленные границы интервала не попадает, с надёжностью P можно утверждать, что использованный метод анализа имеет значимую систематическую погрешность, т.е. дает неправильные результаты (пример 5).
Сравнение экспериментальных данных по воспроизводимости. При сопоставлении двух методик анализа (двух приборов, двух лаборантов и т.п.) по воспроизводимости полученных данных используют статистический критерий Фишера (пример 6): экспериментальное значение F = S12 / S22 сопоставляется с табличным значениями F табл. Следует обратить внимание, что первой дисперсией считают ту, которая больше по абсолютной величине, независимо от того, сколько в каждой выборке вариант и какая серия измерений проводилась раньше. Поэтому Fэксп всегда больше 1. Критические значения F табл отыскивают в таблицах для подходящих значений n 1 и n 2 (df1 и df2) и выбранного уровня значимости (см. приложение 10). Дисперсии считают неоднородными, а серии измерений - достоверно отличающимися по воспроизводимости, если Fэксп >Fтабл. В противном случае различие в воспроизводимости методик считают недоказанным.
Сравнение результатов анализа. Различие между средними арифметическими в двух сериях измерений (анализов) может быть статистически достоверным (в этом случае такое различие будет воспроизводиться при повторении измерений) или случайным. Статистическое сравнение средних значений двух выборок позволяет делать обоснованные выводы из проведенных исследований и поэтому особенно важно для специалиста, независимо от того, в какой именно области науки или техники он работает. Обычно сравнение средних проводится по критерию Стьюдента (пример 7). Сопоставление средних значений по Стьюденту в о з м о ж н о, если: а) в обеих выборках отсутствуют грубые промахи; б) измеряемая величина имеет нормальное распределение; в) дисперсии обеих выборок однородны. Поэтому сравнению средних значений должна предшествовать проверка по критерию Фишера. Экспериментальное значение t- критерия находят по формуле:
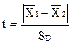 , (35)
, (35)
где в числителе стоят средние арифметические первой и второй выборок, а в знаменателе - обобщенное стандартное отклонение. Последнюю величину считают по-разному:
Sd = 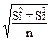 при n1=n2=n. (35а)
при n1=n2=n. (35а)
Sd» 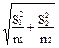 при n1 ¹ n2. (35б)
при n1 ¹ n2. (35б)
При существенном отличии в объеме выборок можно применять и более точные формулы. Величину tэксп сравнивают с табличными значениями для выбранного уровня значимости (см. пример 7), при этом число степеней свободы df = n1 + n2 - 2. Различие средних достоверно, если найденное значение t больше, чем t0,01. Если t меньше, чем t0,05, то различие средних считается статистически недоказанным, однако и в этом случае не следует утверждать, что результаты анализа, представленные данными двух выборок, достоверно совпадают.
Примеры типовых расчетов
1. Титровали пять аликвот одного и того же раствора в одинаковых условиях. Затрачены следующие объёмы титранта (в мл): 20,2; 20,6; 20,3; 19,0; 20,4. Имеются ли среди этих результатов грубые промахи?
Решение. После ранжирования результаты образуют ряд: 19,0; 20,2; 20,4; 20,3; 20,6. Очевидно, наименьший результат 19,0 довольно сильно отличается от других результатов и, возможно, является промахом. Проверяем по Q-тесту:
Q эксп = 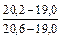 = 1,2 / 1,6 = 0,75 Q табл = 0,73 (для n=5 и P=0,95).
= 1,2 / 1,6 = 0,75 Q табл = 0,73 (для n=5 и P=0,95).
Так как Q эксп > Q табл, проверяемый результат 19,0 с надежностью 0,95 можно считать грубым промахом и, соответственно, его следует отбросить. В выборке останется четыре результата: 20,2; 20,3; 20,4; 20,6. Снова проверим по Q-тесту наименьшую из оставшихся вариант: Q эксп =  = 0,25 Q табл = 0,85 (для n=4 и P=0,95).
= 0,25 Q табл = 0,85 (для n=4 и P=0,95).
Так как Q эксп не превышает критического значения, результат 20,2 оставляем. Проверяя по Q-тесту наибольшую варианту (20,6), также не обнаруживаем грубых промахов.
2. Спектральный анализ одного и того же образца горной породы повторяли девять раз, при этом найденные содержания золота (в граммах на тонну): 38, 66, 37, 35, 33, 16, 36, 39, 32. Вычислить среднее значение и доверительный интервал для P=0,90.
Решение. Вызывают сомнения одновременно два значения: 66 и 16 (наибольшее и наименьшее в выборке). Проверка по Q-тесту в таких случаях неэффективна, используется более трудоемкий, но и более надежный метод максимальных отклонений, при котором грубыми промахами считают те варианты, у которых отклонение от среднего арифметического, выраженное в единицах S (в стандартных отклонениях), превышает критическое (табличное) значение. Для проверки надо сначала подсчитать выборочные параметры по всей исходной выборке: 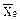 = 36,9; S = 12,9. Сомнительная варианта 16 отличается от среднего арифметического 36,9 на (36,9 -16) / 12,9 = 1,62 стандартных отклонения, а варианта 66 - на 2,26 стандартных отклонения. Критическое же значение максимального относительного отклонения для n = 9 и P = 0,90 равно 2,10. Следовательно, результат, равный 66 г/т, достоверно отличается от других вариант в выборке, его можно с требуемой надежностью 0,90 считать грубым промахом и отбросить. В новой выборке имеется 8 результатов, причем остается одно сомнительное значение - 16. При проверке по Q-тесту оно признается грубым промахом (Qэксп = 0,70, а Qтабл = 0,47) и отбрасывается. В оставшейся выборке из 7 результатов никакая проверка не обнаруживает грубых промахов и проводить статистическую обработку этой выборки по Стьюденту можно.
= 36,9; S = 12,9. Сомнительная варианта 16 отличается от среднего арифметического 36,9 на (36,9 -16) / 12,9 = 1,62 стандартных отклонения, а варианта 66 - на 2,26 стандартных отклонения. Критическое же значение максимального относительного отклонения для n = 9 и P = 0,90 равно 2,10. Следовательно, результат, равный 66 г/т, достоверно отличается от других вариант в выборке, его можно с требуемой надежностью 0,90 считать грубым промахом и отбросить. В новой выборке имеется 8 результатов, причем остается одно сомнительное значение - 16. При проверке по Q-тесту оно признается грубым промахом (Qэксп = 0,70, а Qтабл = 0,47) и отбрасывается. В оставшейся выборке из 7 результатов никакая проверка не обнаруживает грубых промахов и проводить статистическую обработку этой выборки по Стьюденту можно.
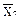 = 35,7 S = 2,6 m Î (35,7 ± 2,6 · 1,94 / Ö7),
= 35,7 S = 2,6 m Î (35,7 ± 2,6 · 1,94 / Ö7),
т.е. m принадлежит интервалу 35,7 ± 1,9. Границами доверительного интервала для P = 0,90 будут значения 33,8 и 37,6. С учетом точности исходных данных их можно округлить до целых значений и считать, что истинное содержание золота в данной горной породе находится между 34 и 38 граммами на тонну.
3. Спектральное определение золота в горной породе проведено 20 раз. Ниже приводятся результаты (в граммах на тонну) после их ранжирования. Грубых промахов и дрейфа не выявлено. Можно ли на основании этих данных считать, что данная методика приводит к нормальному распределению случайных погрешностей?
24; 29; 32; 34; 39; 39; 41; 42;45; 45; 45; 47; 49; 50; 54; 57; 58; 64; 69; 79.
Решение. Рассчитываем коэффициент асимметрии с помощью специальной программы для ПЭВМ по формуле:
g = 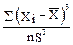 . (36)
. (36)
Получаем g = 0,49 при критическом значении g = 1,01 (для P=0,95). Распределение можно считать симметричным. Далее рассчитываем коэффициент эксцесса:
E =  . (37)
. (37)
Получаем Е = - 0,30 при критическом значении абсолютной величины этого коэффициента, равном 1,75. Следовательно, распределение не имеет достоверно выраженного эксцесса. Отсутствие достоверной асимметрии и эксцесса позволяет считать распределение нормальным.
4. При анализе пяти проб одной и той же нефти на содержание сульфидной серы были затрачены следующие объёмы титранта (в миллилитрах): 20,2; 20,6; 20,3; 20,5; 20,4. Рассчитайте интервал, в котором с надёжностью r= 0,95 находится «истинное значение» объёма титранта, соответствующее истинному содержанию определяемого компонента в пробе. Систематические ошибки титрования отсутствуют.
Решение. Так как дрейф результатов не заметен, а грубые промахи по Q-тесту не обнаруживаются, можно рассчитывать среднее арифметическое выборки и её стандартное отклонение. Получаем 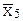 = 20,4 мл, S = 0,16 мл. Предполагаем, что методика анализа дает нормальное распределение случайных погрешностей, в этом случае расчет доверительного интервала проводим по методу Стьюдента. Коэффициент Стьюдента находим в приложении 9. Для df=4 и P=0,95 значение t равно 2,78, откуда m= 20,4 ± 2,78 · 0,16 / √5 = 20,40 ± 0,20 (мл). Полуширину доверительного интервала принято записывать с одной значащей цифрой и соответственно ей округлять средний результат анализа. В данном случае получаем (20,4 ± 0,2) мл. Результат может быть записан и по-другому: V = 20,2 ¸ 20,6 (мл). Однако истинному содержанию сульфидной серы этот интервал объемов титранта соответствует только в отсутствие систематических погрешностей!
= 20,4 мл, S = 0,16 мл. Предполагаем, что методика анализа дает нормальное распределение случайных погрешностей, в этом случае расчет доверительного интервала проводим по методу Стьюдента. Коэффициент Стьюдента находим в приложении 9. Для df=4 и P=0,95 значение t равно 2,78, откуда m= 20,4 ± 2,78 · 0,16 / √5 = 20,40 ± 0,20 (мл). Полуширину доверительного интервала принято записывать с одной значащей цифрой и соответственно ей округлять средний результат анализа. В данном случае получаем (20,4 ± 0,2) мл. Результат может быть записан и по-другому: V = 20,2 ¸ 20,6 (мл). Однако истинному содержанию сульфидной серы этот интервал объемов титранта соответствует только в отсутствие систематических погрешностей!
5. Содержание углерода в некотором органическом веществе, вычисленное по его формуле, равно 90,05 %. Анализ того же вещества в лаборатории дал результаты 89,6; 90,0; 89,8 %., причем примесей других веществ в анализируемой пробе нет. Имеет ли используемая методика анализа систематическую ошибку?
Решение. 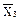 .= 89,8%; n = 3; выбираем P = 0,95. В этом случае t = 4,30. Из приведённых в условии данных следует, что S = 0,20%. Рассчитываем доверительный интервал для среднего арифметического:
.= 89,8%; n = 3; выбираем P = 0,95. В этом случае t = 4,30. Из приведённых в условии данных следует, что S = 0,20%. Рассчитываем доверительный интервал для среднего арифметического:
% C = 89,8 ± 0,20 · 4,30 / √3 = 89,8 ± 0,5 (%).
Так как истинное значение входит в границы доверительного интервала 89,3 % ¸90,3 %, следовательно, несмотря на то, что во всех проведённых измерениях мы получили заниженные значения, статистически достоверная систематическая погрешность не выявлена. Можно считать, что методика позволяет правильно оценить содержание углерода.
6. Жёсткость одной и той же природной воды определяли с разными индикаторами. Получены результаты (в ммоль/л). Какой из индикаторов позволяет более воспроизводимо определять жёсткость?
Индикатор ЭХЧ - Т: 7,45; 7,40; 7,33; 7,50; 7,48; 9,13; 7,42;
Индикатор кальмагит: 7,87; 7,91; 8,02; 7,96.
Решение. Результат 9,13 в серии ЭХЧ -Т выглядит сомнительным. Проверка по Q -тесту подтверждает, что это грубый промах. Так как критерий Фишера применяется только в отсутствие промахов, результат 9,13 из дальнейшей обработки исключается. По оставшимся результатам рассчитывают дисперсии: для ЭХЧ -Т S2 = 37,6·10-4, для кальмагита - 42,0·10-4. Так как при использовании кальмагита дисперсия больше, соответствующую серию измерений считаем первой. Получаем: n1 = 4, df1 = 3; n2 =6, df2=5. Табличное значение критерия Фишера для P = 0,95 при df1 =3 и df2 =5 равно 5,4, тогда как значение Fэксп =42,0 / 37,6 = 1,12. Так как Fэксп< Fтабл, то обе дисперсии считаем однородными. Таким образом, приведенные данные не позволяют выявить статистически достоверного различия в воспроизводимости двух методик определения жесткости воды. Очевидно, использование ЭХЧ-Т и кальмагита приводит к практически одинаковой воспроизводимости результатов[9].
7. Пользуясь данными примера 6, установите, имеется ли достоверное различие в средних результатах определения жесткости воды с двумя разными индикаторами.
Решение. После исключения грубого промаха 9,13 первая серия результатов (с ЭХЧ-Т) имеет 6 вариант, вторая - 4. Ранее (пример 6) было установлено, что дисперсии обеих выборок однородны. Известно, что результаты титрования при достаточно больших n распределяются по нормальному закону. Все это дает основание проводить сравнение средних по t-критерию.Обобщенное стандартное отклонение Sd приближенно равно: 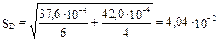 . Более точные расчетные формулы дают SD = 4,1·10-2. Средние значения жесткости (в ммоль/л) составляют в первой серии - с ЭХЧ-Т: 7,43, а во второй - 7,94. Сдвиг средних значений составляет 0,51. Экспериментальное значение t = 0,51 / 0,04 = 12,6. Табличное же значение t при a=0,05 и df = 6 + 4 - 2 = 8 равно 2,31. Так как экспериментальное значение t значительно больше, чем табличное, мы можем считать достоверно доказанным различие средних значений. Судя по полученным данным, определение жесткости с кальмагитом всегда будет приводить к более высоким значениям, чем титрование с ЭХЧ-Т.
. Более точные расчетные формулы дают SD = 4,1·10-2. Средние значения жесткости (в ммоль/л) составляют в первой серии - с ЭХЧ-Т: 7,43, а во второй - 7,94. Сдвиг средних значений составляет 0,51. Экспериментальное значение t = 0,51 / 0,04 = 12,6. Табличное же значение t при a=0,05 и df = 6 + 4 - 2 = 8 равно 2,31. Так как экспериментальное значение t значительно больше, чем табличное, мы можем считать достоверно доказанным различие средних значений. Судя по полученным данным, определение жесткости с кальмагитом всегда будет приводить к более высоким значениям, чем титрование с ЭХЧ-Т.
Контрольные вопросы
1. Дайте определение таким терминам, как выборка, варианта, стандартное отклонение, дисперсия, доверительный интервал.
2. Объясните различие между случайными и систематическими погрешностями.
3. Какие причины обычно ведут к появлению случайных погрешностей анализа, систематических?
4. Что такое грубые промахи, каковы могут быть причины их появления в ходе титриметрического анализа, как они выявляются?
5. Что такое дрейф? Приведите пример соответствующей выборки и поясните причины, по которым мог появиться дрейф.
6. Какими математическими формулами описывается нормальное распределение результатов анализа? Почему оно так называется? Какие еще распределения вам известны?
7. Как проверить, подчиняются ли результаты анализа по некоторой методике закону нормального распределения?
8. Как подсчитать границы доверительного интервала по Стьюденту? В каких случаях такой расчет даст неверные результаты?
9. От каких факторов и как именно зависит величина t (коэффициента Стьюдента) в формуле для расчета доверительного интервала?
10. Как проверить, имеется ли в результатах анализа систематическая погрешность?
11. Две лаборатории выдали различные результаты анализа одного и того же исследуемого объекта. Как проверить, какая из них дала правильные, а какая - неверные результаты?
12. В каких случаях расхождение между средними результатами анализа воды до и после ее очистки можно считать достоверным (статистически значимым)?
13. Во сколько раз могут отличаться дисперсии результатов анализа, полученные в двух разных лабораториях, чтобы мы еще могли считать соответствующие методики практически одинаковыми по воспроизводимости? В обеих лабораториях проведено по 3 параллельных анализа.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Указания. В данном разделе вначале даны несложные типовые задачи, алгоритм решения которых очевиден и сводится к подстановке данных в известные формулы. Для вычислений рекомендуется использовать микрокалькуляторы, у которых имеются операции логарифмирования и потенцирования. Во всех случаях, где вид растворителя и температура раствора в условии задачи не указаны, следует иметь в виду водные растворы и температуру 25°С. При переводе процентных концентраций в молярные и наоборот следует считать плотность раствора равной 1,0000 г/см3, за исключением решения тех задач, в условии которых прямо указана иная плотность раствора. Во всех случаях обращайте внимание на точность исходных данных, которым должна соответствовать точность получаемого ответа.
Обратите внимание на то, что в условиях некоторых типовых задач имеются «лишние» исходные данные, а в других таких данных недостает. Так часто бывает в практике, а поэтому, решая задачу, подумайте вначале, все ли необходимые числовые данные имеются в условии задачи, можно ли найти недостающие в справочниках, или данную задачу вообще нельзя решить.
Во второй части данного раздела содержатся более сложные задачи нетрадиционного типа, моделирующие проблемные ситуации, с которыми сталкивается химик-аналитик при разработке новых или проверке известных методик анализа. Из этих проблемных ситуаций можно выйти, проведя некоторые расчеты. При решении соответствующих задач следует вначале наметить путь решения, разобраться, какие справочные данные потребуются для выполнения необходимых расчетов, отыскать эти данные в справочниках, а затем провести сам расчет и проверку полученного ответа. Для большинства задач целесообразно проводить расчеты, применяя компьютер с необходимым программным обеспечением. Нетрадиционные задачи обычно допускают несколько вариантов решения, интересно и полезно попытаться решить каждую задачу несколькими способами.
Поскольку для решения таких задач необходимо использовать материал не одного, а ряда разделов учебного курса, их целесообразно решать при подготовке к экзамену по аналитической химии. В настоящем пособии они не систематизированы соответственно тематике практических занятий, в отличие от типовых задач.
Типовые задачи



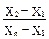 , (32)
, (32)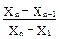 , (32а)
, (32а)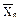 - среднее арифметическое из всех n вариант,
- среднее арифметическое из всех n вариант,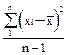 ; S =
; S = 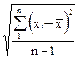 . (33)
. (33)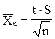 £ m £
£ m £ 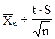 (34)
(34)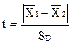 , (35)
, (35)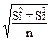 при n1=n2=n. (35а)
при n1=n2=n. (35а)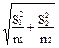 при n1 ¹ n2. (35б)
при n1 ¹ n2. (35б)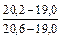 = 1,2 / 1,6 = 0,75 Q табл = 0,73 (для n=5 и P=0,95).
= 1,2 / 1,6 = 0,75 Q табл = 0,73 (для n=5 и P=0,95). = 0,25 Q табл = 0,85 (для n=4 и P=0,95).
= 0,25 Q табл = 0,85 (для n=4 и P=0,95).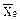 = 36,9; S = 12,9. Сомнительная варианта 16 отличается от среднего арифметического 36,9 на (36,9 -16) / 12,9 = 1,62 стандартных отклонения, а варианта 66 - на 2,26 стандартных отклонения. Критическое же значение максимального относительного отклонения для n = 9 и P = 0,90 равно 2,10. Следовательно, результат, равный 66 г/т, достоверно отличается от других вариант в выборке, его можно с требуемой надежностью 0,90 считать грубым промахом и отбросить. В новой выборке имеется 8 результатов, причем остается одно сомнительное значение - 16. При проверке по Q-тесту оно признается грубым промахом (Qэксп = 0,70, а Qтабл = 0,47) и отбрасывается. В оставшейся выборке из 7 результатов никакая проверка не обнаруживает грубых промахов и проводить статистическую обработку этой выборки по Стьюденту можно.
= 36,9; S = 12,9. Сомнительная варианта 16 отличается от среднего арифметического 36,9 на (36,9 -16) / 12,9 = 1,62 стандартных отклонения, а варианта 66 - на 2,26 стандартных отклонения. Критическое же значение максимального относительного отклонения для n = 9 и P = 0,90 равно 2,10. Следовательно, результат, равный 66 г/т, достоверно отличается от других вариант в выборке, его можно с требуемой надежностью 0,90 считать грубым промахом и отбросить. В новой выборке имеется 8 результатов, причем остается одно сомнительное значение - 16. При проверке по Q-тесту оно признается грубым промахом (Qэксп = 0,70, а Qтабл = 0,47) и отбрасывается. В оставшейся выборке из 7 результатов никакая проверка не обнаруживает грубых промахов и проводить статистическую обработку этой выборки по Стьюденту можно.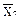 = 35,7 S = 2,6 m Î (35,7 ± 2,6 · 1,94 / Ö7),
= 35,7 S = 2,6 m Î (35,7 ± 2,6 · 1,94 / Ö7),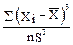 . (36)
. (36) . (37)
. (37)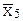 = 20,4 мл, S = 0,16 мл. Предполагаем, что методика анализа дает нормальное распределение случайных погрешностей, в этом случае расчет доверительного интервала проводим по методу Стьюдента. Коэффициент Стьюдента находим в приложении 9. Для df=4 и P=0,95 значение t равно 2,78, откуда m= 20,4 ± 2,78 · 0,16 / √5 = 20,40 ± 0,20 (мл). Полуширину доверительного интервала принято записывать с одной значащей цифрой и соответственно ей округлять средний результат анализа. В данном случае получаем (20,4 ± 0,2) мл. Результат может быть записан и по-другому: V = 20,2 ¸ 20,6 (мл). Однако истинному содержанию сульфидной серы этот интервал объемов титранта соответствует только в отсутствие систематических погрешностей!
= 20,4 мл, S = 0,16 мл. Предполагаем, что методика анализа дает нормальное распределение случайных погрешностей, в этом случае расчет доверительного интервала проводим по методу Стьюдента. Коэффициент Стьюдента находим в приложении 9. Для df=4 и P=0,95 значение t равно 2,78, откуда m= 20,4 ± 2,78 · 0,16 / √5 = 20,40 ± 0,20 (мл). Полуширину доверительного интервала принято записывать с одной значащей цифрой и соответственно ей округлять средний результат анализа. В данном случае получаем (20,4 ± 0,2) мл. Результат может быть записан и по-другому: V = 20,2 ¸ 20,6 (мл). Однако истинному содержанию сульфидной серы этот интервал объемов титранта соответствует только в отсутствие систематических погрешностей!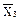 .= 89,8%; n = 3; выбираем P = 0,95. В этом случае t = 4,30. Из приведённых в условии данных следует, что S = 0,20%. Рассчитываем доверительный интервал для среднего арифметического:
.= 89,8%; n = 3; выбираем P = 0,95. В этом случае t = 4,30. Из приведённых в условии данных следует, что S = 0,20%. Рассчитываем доверительный интервал для среднего арифметического: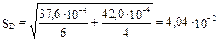 . Более точные расчетные формулы дают SD = 4,1·10-2. Средние значения жесткости (в ммоль/л) составляют в первой серии - с ЭХЧ-Т: 7,43, а во второй - 7,94. Сдвиг средних значений составляет 0,51. Экспериментальное значение t = 0,51 / 0,04 = 12,6. Табличное же значение t при a=0,05 и df = 6 + 4 - 2 = 8 равно 2,31. Так как экспериментальное значение t значительно больше, чем табличное, мы можем считать достоверно доказанным различие средних значений. Судя по полученным данным, определение жесткости с кальмагитом всегда будет приводить к более высоким значениям, чем титрование с ЭХЧ-Т.
. Более точные расчетные формулы дают SD = 4,1·10-2. Средние значения жесткости (в ммоль/л) составляют в первой серии - с ЭХЧ-Т: 7,43, а во второй - 7,94. Сдвиг средних значений составляет 0,51. Экспериментальное значение t = 0,51 / 0,04 = 12,6. Табличное же значение t при a=0,05 и df = 6 + 4 - 2 = 8 равно 2,31. Так как экспериментальное значение t значительно больше, чем табличное, мы можем считать достоверно доказанным различие средних значений. Судя по полученным данным, определение жесткости с кальмагитом всегда будет приводить к более высоким значениям, чем титрование с ЭХЧ-Т.


