

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...
Топ:
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Интересное:
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Метод минимизации функции с помощью карт Вейча обеспечивает простоту получения результатов. Он используется при минимизации относительно несложных функций (с числом аргументов до пяти). Карта Вейча представляет собой определенную форму таблицы истинности. Табл. 6 являются картами Вейча для функций соответственно двух (а), трех (б), четырех (в) аргументов.
Таблица 6

Каждая клетка карты соответствует некоторому набору значений аргументов. Этот набор аргументов определяется присвоением значения лог.1 буквам, на пересечении строк и столбцов которых расположена клетка. Так, в карте функций четырех аргументов (табл. 6в) клетки первой строки соответствуют следующим комбинациям значений аргументов:
1-я клетка 

Число клеток карты равно числу всех возможных наборов значений аргументов  (п — число аргументов функций). В каждую из клеток карты записывается значение функции на соответствующем этой клетке наборе значений аргументов. Пусть функция задана таблицей истинности (табл. 7). Таблица истинности этой функции в форме карты Вейча представлена табл. 8.
(п — число аргументов функций). В каждую из клеток карты записывается значение функции на соответствующем этой клетке наборе значений аргументов. Пусть функция задана таблицей истинности (табл. 7). Таблица истинности этой функции в форме карты Вейча представлена табл. 8.
Таблица 7

Карта Вейча определяет значения функции на всех возможных наборах значений аргументов и является таблицей истинности. Карты Вейча компактны, но главное их достоинство состоит в следующем. При любом переходе из одной клетки в соседнюю вдоль столбца или строки изменяется значение лишь одного аргумента функции. Следовательно, если в паре соседних клеток содержится 1, то над соответствующими им членами канонической формы может быть проведена операция склеивания. Таким образом, облегчается поиск склеиваемых членов.
Таблица 8Таблица 9
|
|
Сформулируем правила получения МДНФ функций с помощью карт Вейча. Все клетки, содержащие 1, объединяются в замкнутые области. При этом каждая область должна представлять собой прямоугольник с числом клеток 2 k, где k - 0, 1, 2,.... Значит, допустимое число клеток в области 1, 2, 4, 8,...,. Области могут пересекаться и одни и те же клетки могут входить в разные области. Затем проводится запись выражения МДНФ функции. Каждая из областей в МДНФ представляется членом, число букв в котором на k меньше общего числа аргументов функции п (т.е. равно 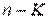 ). Каждый член МДНФ составляется лишь из тех аргументов, которые для клеток соответствующей области имеют одинаковое значение (без инверсии либо с инверсией).
). Каждый член МДНФ составляется лишь из тех аргументов, которые для клеток соответствующей области имеют одинаковое значение (без инверсии либо с инверсией).
Таким образом, при охвате клеток замкнутыми областями следует стремиться, чтобы число областей было минимальным (при этом минимальным будет число членов в МДНФ функции), а каждая область содержала возможно большее число клеток (при этом минимальным будет число букв в членах МДНФ функции).
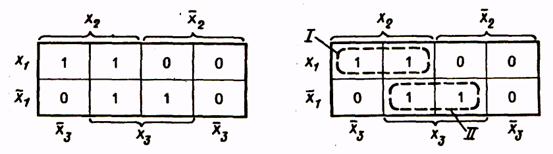
Рассмотрим минимизацию с помощью карты Вейча функции трех аргументов, представленной табл. 9. Все клетки, содержащие 1, охватываются двумя областями. В каждой из областей 21 клеток, для них n-k = 3-l = 2, и эти области в МДНФ будут представлены членами, содержащими по две буквы. Первой области соответствует член 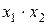 (аргумент
(аргумент  здесь не присутствует, так как для одной клетки этой области он имеет значение без инверсии, для другой — с инверсией); второй области соответствует член
здесь не присутствует, так как для одной клетки этой области он имеет значение без инверсии, для другой — с инверсией); второй области соответствует член 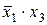 . Следовательно, МДНФ функции
. Следовательно, МДНФ функции
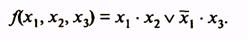
Рассмотрим пример минимизации функции четырех аргументов, заданной табл. 10. Первая и четвертая области имеют по две клетки, для них п- k - 4 -1=3. Эти области в МДНФ будут представлены членами, содержащими по три буквы. Вторая и третья области содержат по четыре клетки и в МДНФ выражаются членами, содержащими по две буквы (п - k = 4 -2 = 2). Минимальная ДНФ функции
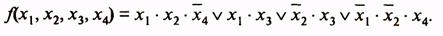
Таблица 10Таблица 11
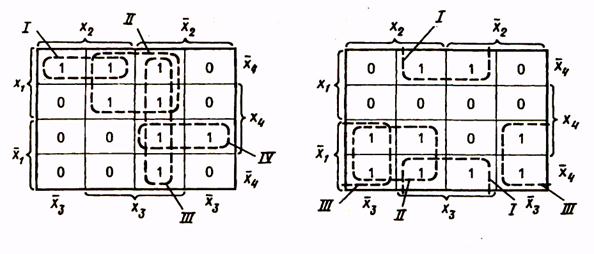
При построении замкнутых областей допускается сворачивание карты в цилиндр с объединением ее противоположных граней. В силу этого крайние клетки строки или столбца таблицы рассматриваются как соседние и могут быть объединены в общую область. Иллюстрацию этого приема проведем на примере функции, представленной табл. 11. Минимальная ДНФ функции
|
|
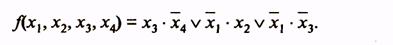
В силу допустимости такого сворачивания карты вдоль горизонтальной и вертикальной осей, например: клетки, расположенные в четырех углах карты функции четырех переменных, оказываются соседними и могут быть объединены в одну область. Покажем это на примере минимизации функции, заданной табл. 12. Минимальная ДНФ функции
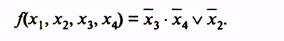
Таблица 12Таблица 13
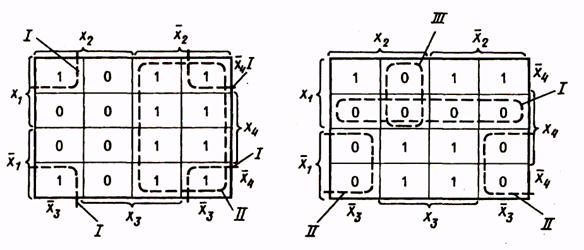
Для получения МКНФ функции замкнутыми областями охватываются клетки с нулевыми значениями функции, и при записи членов логического выражения берутся инверсии аргументов, на пересечении которых находятся области. Так, для функции, приведенной в табл. 13, МКНФ
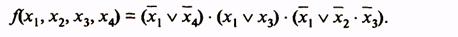
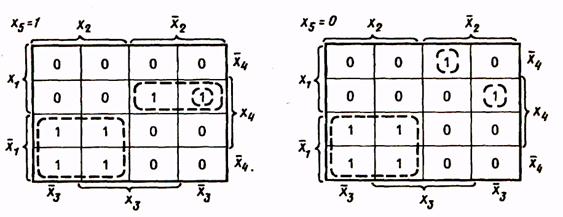
До сих пор рассматривались логические функции с числом аргументов до четырех. Представление функции и минимизация ее с помощью карт Вейча усложняются, если число аргументов больше четырех. В табл. 14 показано представление с помощью карт Вейча функции пяти аргументов.
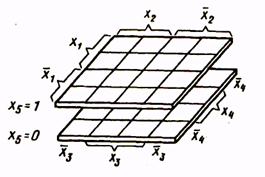 Рис.3 Рис.3
| Таблица истинности здесь состоит из двух карт, каждая из которых представляет собой карту четырех переменных. Одна из них соответствует х5= 1, другая - х5 = 0. Эти карты можно мысленно расположить одна над другой (рис.3). При этом области охвата клеток могут быть трехмерными, т.е. одной областью могут охватываться клетки двух карт. |
Для функции, приведенной в табл. 23, МДНФ

Таблица 14
Для минимизации функции с числом аргументов, большим пяти, карты Вейча оказываются неудобными. Минимизация таких функций может быть выполнена методом Квайна.
Пример. 2. Пусть функция 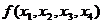 задана картой Карно.
задана картой Карно. 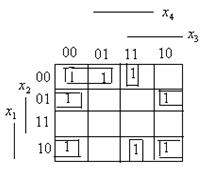

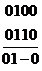
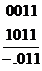
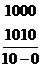

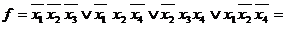
2.. Пусть функция 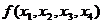 задана картой Карно.
задана картой Карно.

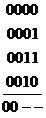
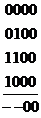
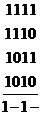
В результате минимизации получится функция

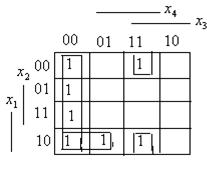
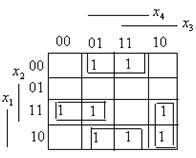
3.. Пусть функция 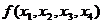 задана картой Карно.
задана картой Карно.
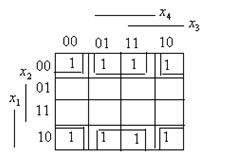
Здесь имеется два четырехклеточных подквадрата.
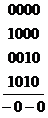

В результате получится функция
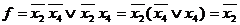
Эту задачу можно решить иначе, если рассматривать один восьмиклеточный подквадрат
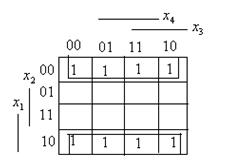
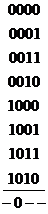 Отсюда сразу получается результат
Отсюда сразу получается результат 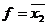 ,
,
Таким образом, задача минимизации сводится к геометрической задаче отыскания правильных конфигураций. При использовании карты Карно нужно стремиться объединить единичные клетки в подквадраты с возможно большим числом клеток, чтобы количество подквадратов было как можно меньше. При решении задачи таким способом могут получиться объединения клеток в одинаковое число подквадратов с одним и тем же числом клеток. Каждый из таких вариантов будет соответствовать одной из минимальных форм функции.
|
|
 Следует отметить, что не всегда матричный метод оказывается эффективным. Пусть, например нужно минимизировать функцию
Следует отметить, что не всегда матричный метод оказывается эффективным. Пусть, например нужно минимизировать функцию
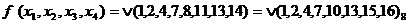
Карта Карно в этом случае имеет вид

Размещение единиц здесь таково, что их нельзя объединить в подквадраты. В то же время функцию легко минимизировать методом Блейка.
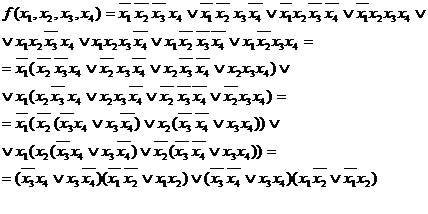
С помощью матрицы Карно можно найти минимальное выражение для функции не только в дизъюнктивной форме, но и в конъюктивной форме. Для этого в карте Карно необходимо выбирать подквадраты из нулей, а не из единиц и помнить о том, что в этом случае 0~x, а 1~  .
.
Пример. Найти минимальную функцию в к.н.ф, если 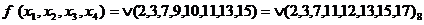 .
.
Составим  , она содержит в СДНФ конъюнкции, которых нет в СДНФ функции
, она содержит в СДНФ конъюнкции, которых нет в СДНФ функции 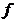 . Они соответствуют тем клеткам матрицы, которых стоит 0
. Они соответствуют тем клеткам матрицы, которых стоит 0

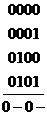 .
. 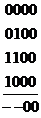

Отсюда получим  =
=  . Найдем теперь отрицание от левой и правой частей этого равенства. В результате получим
. Найдем теперь отрицание от левой и правой частей этого равенства. В результате получим 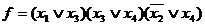
Полученное выражение является минимальной КНФ.
Матричный метод является наиболее эффективным при решении задачи минимизации функций четырех переменных. Для большего числа переменных его использовать затруднительно. При пяти и шести переменных приходится прибегать к некоторым преобразованиям функции для того, чтобы в дальнейшем можно было использовать матричный метод. Например, если имеется функция пяти переменных, то можно вынести за одну скобку некоторую переменную, а за вторую скобку ее отрицание. Тогда внутри скобок окажется функция четырех переменных, которую можно минимизировать матричным методом.
Пример.
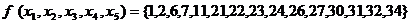

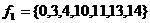
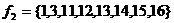
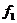
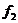
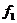 :
: 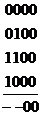
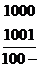


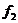 :
: 

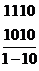
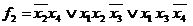
2 М инимизация булевых функций методом Квайна– Мак-Класки.
Импликантой 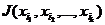 функции
функции  называется конъюнкция некоторых аргументов из набора
называется конъюнкция некоторых аргументов из набора 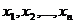 и их отрицаний, обладающая следующими свойствами:
и их отрицаний, обладающая следующими свойствами:
|
|
1) Если на некотором наборе 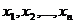 импликанта
импликанта  принимает значение 1, то и
принимает значение 1, то и 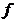 принимает на этом наборе значение 1.
принимает на этом наборе значение 1.
2 При исключении хотя бы одного множителя из  свойство 1) не выполняется.
свойство 1) не выполняется.
Пример. 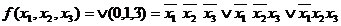 ,
,
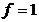 на наборах (0,0,0), (0,0,1), (0,1,1).
на наборах (0,0,0), (0,0,1), (0,1,1).
Рассмотрим  ,
, 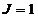 на наборах (0,0,0), (0,0,1). На этих наборах
на наборах (0,0,0), (0,0,1). На этих наборах 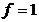 , т.е. выполняется условие 1).
, т.е. выполняется условие 1).
Если вычеркнуть один множитель из  и оставить, например,
и оставить, например, 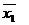 , то.
, то. 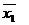 принимает значение 1 на наборах (0 0 0), (0 0 1), (0 1 0), (0 11), причем на выделенном наборе
принимает значение 1 на наборах (0 0 0), (0 0 1), (0 1 0), (0 11), причем на выделенном наборе 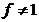 . Аналогичным образом,
. Аналогичным образом, 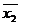 принимает значение 1, причем на выделенных наборах
принимает значение 1, причем на выделенных наборах 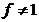 . Следовательно, при вычеркивании одного множителя у
. Следовательно, при вычеркивании одного множителя у  свойство 1) не выполняется. Это означает, что
свойство 1) не выполняется. Это означает, что  является импликантой функции.
является импликантой функции.
Пусть на некотором наборе 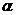 функция
функция 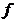 обращается в 1. Если на этом наборе импликанта
обращается в 1. Если на этом наборе импликанта  функции обращается в 1, то говорят, что импликанта
функции обращается в 1, то говорят, что импликанта  накрывает эту единицу функции
накрывает эту единицу функции 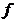 .
.
Система импликант функции 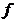 называется полной, если любая единица из таблицы значений функции
называется полной, если любая единица из таблицы значений функции 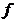 накрывается хотя бы одной импликантой.
накрывается хотя бы одной импликантой.
Сокращенной ДНФ функции 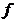 называется дизъюнкция всех импликант из полной системы импликант.
называется дизъюнкция всех импликант из полной системы импликант.
Утверждение. Сокращенная ДНФ. функции 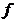 совпадает с самой функцией.
совпадает с самой функцией.
Действительно, дизъюнкция всех импликант из полной системы импликант равна 1 на тех наборах, где равна 1 функция (в соответствии с определением импликанты 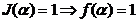 ) и равна нулю на тех наборах, где равна нулю функция, т.е. значения сокращенной д.н.ф. функции
) и равна нулю на тех наборах, где равна нулю функция, т.е. значения сокращенной д.н.ф. функции 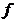 и функции
и функции 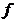 совпадают.
совпадают.
Сокращенная д.н.ф. функции 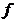 содержит меньшее число букв, чем СДНФ Однако, во многих случаях допускается дальнейшее сокращение числа букв за счет того, что некоторые из импликант могут поглощаться дизъюнкциями других импликант.
содержит меньшее число букв, чем СДНФ Однако, во многих случаях допускается дальнейшее сокращение числа букв за счет того, что некоторые из импликант могут поглощаться дизъюнкциями других импликант.
Система импликант функции 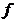 называется приведенной, если эта система полна, а никакая ее часть не является полной системой импликант функции
называется приведенной, если эта система полна, а никакая ее часть не является полной системой импликант функции 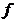 .
.
Тупиковой ДНФ называется дизъюнкция всех импликант, составляющих приведенную систему.
Тупиковая ДНФ- выражение, полученное из сокращенной ДНФ, дальнейшее упрощение которого невозможно в рамках ДНФ.
Минимальной ДНФ называется тупиковая ДНФ, состоящая из наименьшего числа букв.
Одна и та же сокращенная ДНФ может иметь несколько тупиковых ДНФ и несколько минимальных ДНФ.
Процесс минимизации на первом этапе сводится к построению полной системы импликант, затем приведенной системы существенных импликант, из которых строится сокращенная ДНФ, затем строятся тупиковые ДНФ и затем уже выбирается минимальная ДНФ. Решение задачи осуществляется в соответствии со схемой
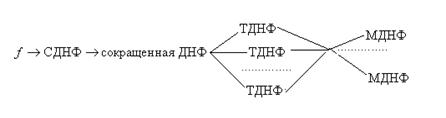
Получение сокращенной ДНФ (нахождение импликантов функции 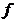 ).
).
|
|
Пример 1.
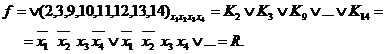
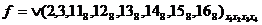

Получение сокращенной ДНФ основывается на законе склеивания 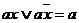 . Из него следует, что можно склеивать или объединять минтермы, отличающиеся только одним сомножителем. Будем склеивать не минтермы, а наборы. Выпишем все наборы переменных, соответствующие минтермам, входящим в разложение функции, в столбик, разбивая их на группы так, чтобы в каждую группу входили наборы с одинаковым числом единиц.
. Из него следует, что можно склеивать или объединять минтермы, отличающиеся только одним сомножителем. Будем склеивать не минтермы, а наборы. Выпишем все наборы переменных, соответствующие минтермам, входящим в разложение функции, в столбик, разбивая их на группы так, чтобы в каждую группу входили наборы с одинаковым числом единиц.
Проводим попарное склеивание наборов из соседних групп (для склеивания наборы должны отличаться на одну переменную). При склеивании общие элементы сохраняются, а элементы, которыми различаются наборы, заменяются чертой. Наборы, участвующие в склеивании, помечаются *. В результате образуется второй столбец, к которому также применяется операция склеивания. При этом склеивают наборы из соседних групп с одинаковым положением черточек. Далее образуется 3-й столбец и т.д. Процесс продолжается до тех пор, пока склеивание возможно.
| N Груп пы | Наборы |  набора
набора
| |||||
| 1 | 0010 * | 2 * | 2,3 | 001– * | 2,3, .10,11 | –01– 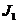
| |
| 2,10 | –010 * | 2,10, 3,11 | –01– 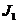
| ||||
| 2 | 0011 * | 3 * | 3,11 | –011 * | |||
| 1001 * | (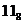 )9 * )9 *
| 9,11 | 10–1 | 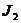
| |||
| 1010 * | 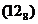 10 * 10 *
| 9,13 | 1–01 | 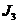
| |||
| 1100 * | (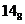 )12 * )12 *
| 10,11 | 101– * | ||||
| 10,14 | 1–10 | 
| |||||
| 12,13 | 110– | 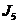
| |||||
| 12,14 | 11–0 | 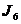
| |||||
| 3 | 1011 * | (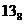 )11 * )11 *
| |||||
| 1101 * | (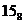 ) 13 * ) 13 *
| ||||||
| 1110 * | 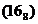 14 * 14 *
| ||||||

Импликантами функции 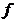 будут наборы во всех столбцах, не участвующие в склеивании (не помеченные).
будут наборы во всех столбцах, не участвующие в склеивании (не помеченные).
 ,
, 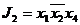 ,
,  ,
, 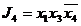 ,
, 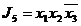 ,
, 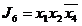 .
.
Сокращенная ДНФ 
 , ее длина составляет 17 букв
, ее длина составляет 17 букв


На рис. изображены импликанты и склеиваемые наборы переменных.
Отметим, что на рисунке номера наборов приведены в восьмеричной системе счисления.
2. Следующий этап – построение тупиковой ДНФ. Для этого нужно составить импликантную таблицу. Строки этой таблицы обозначены импликантами функции, а столбцы минтермами функции. Каждая импликанта является частью какого-нибудь дизъюнктивного члена в СДНФ и обращается в единицу на том же наборе, что и соответствующий минтерм. На пересечении строки, в которой записана импликанта, и столбцов соответствующих минтермов, частью которых является импликанта, поставим крестики. Тупиковые формы являются дизъюнкциями тех импликантов, которые накрывают все минтермы, т.е. в таблице нужно выбрать такие строки, чтобы во всех столбцах был как минимум один плюс.
Чтобы построить тупиковую форму, нужно выбрать минимальное число строк, покрывающих крестиками все столбцы. Ясно, что в систему выбранных строк должны обязательно входить строки, содержащие плюсы, которые являются единственными в столбце. Такие строки называются базисными. Простые импликанты, стоящие в базисных строках, образуют ядро рассматриваемой функции. Обведем кружочками плюсы в строках, соответствующих этим импликантам. Из оставшихся импликант выбираем минимальное число таких, которые покрывают крестиками все свободные столбцы (т.е. те, которые не содержат  ).
).
Импликантная таблица
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 0010 | 0011 | 1001 | 1010 | 1100 | 1011 | 1101 | 1110 | |
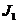 –01– –01–
| 
| 
| + | + | ||||
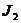 10–1 10–1
| + | + | ||||||
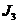 1–01 1–01
| + | + | ||||||
 1–10 1–10
| + | + | ||||||
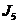 110– 110–
| + | + | ||||||
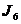 11–0 11–0
| + | + |
В тупиковую ДНФ обязательно должна входить 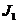 , иначе первые два столбца не накрываются. Следовательно, первая строка является базисной, а импликанта
, иначе первые два столбца не накрываются. Следовательно, первая строка является базисной, а импликанта 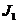 образует ядро функции. При таком выборе автоматически накрываются и еще два столбца. Тупиковыми импликантами являются
образует ядро функции. При таком выборе автоматически накрываются и еще два столбца. Тупиковыми импликантами являются
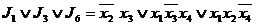 (
(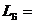 8)
8)
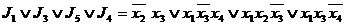 (
(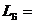 11)
11)
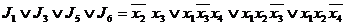 (
(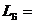 11)
11)
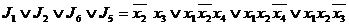 (
(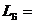 11)
11)
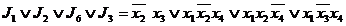 (
(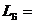 11)
11)
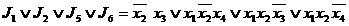 (
(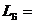 11)
11)
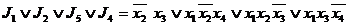 (
(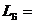 11)
11)
На рисунке изображены все тупиковые ДНФ:
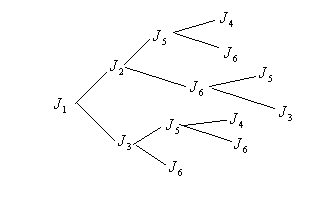
Среди всех тупиковых ДНФ выбираем ДНФ наименьшей длины:
МДНФ: 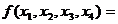
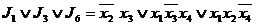
|
|
|

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!