Правило минимизации.
Для получения минимальной функции НДФ (или МНДФ) охватывают областями все клетки, имеющие значение 1 и являющиеся соседними. Эти области должны быть прямоугольной формы и содержать чётное количество клеток. Для каждой области записывается неизменяющаяся часть объедененных минтерм. При этом минимизируемые области могут иметь общие минтермы (пересекаться). В заключение все минтермы суммируются.
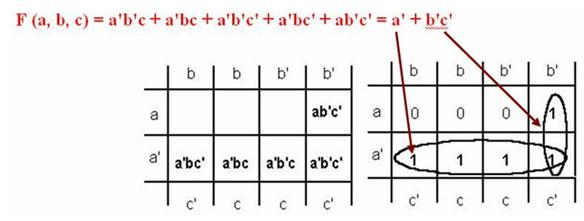
Рис. 4.3.4. Пример минимизации трех переменных с помощью карты Карно
В данном примере, произведения, образующие квадрат (с учётом замкнутости краевых линий диаграммы), позволяют исключить из общего выражения две переменные. При этом количество минтерм также сократилось.
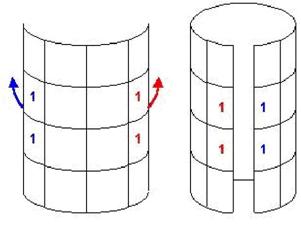
Рис. 4.3.5. Метод скручивания карты Карно
Крайние квадраты карты являются соседними при ее скручивании. Это значит, что они тоже подлежат минимизации. На плоскости можно изобразить карту Карно для 4-х переменных. Для 5 и более переменных необходимы объемные фигуры.
 Пример
Пример
Допустим, что задана логическая функция с помощью таблицы истинности.
Рис. 4.3.6. Пример создания логической функции
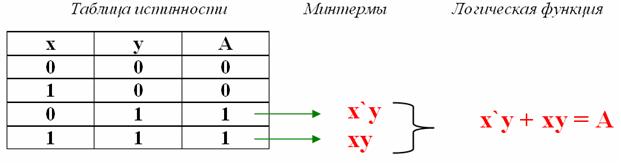
Составим карту Карно, объеденим единицы и получим минимальную форму функции.
Рис. 4.3.7. Пример минимизации
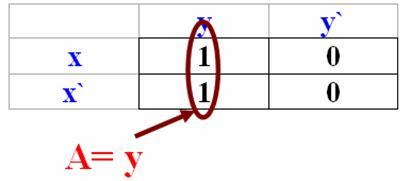
Переменная х изменяется, и поэтому её можно упустить!
Минимизация булевых функций.
Совершенные нормальные формы записи логических функций дают однозначное представление логических функций, но иногда являются очень громоздкими. Поэтому для булевых функций, представленных в виде СДНФ или СКНФ, возникает задача минимизации.
Рассмотрим функцию 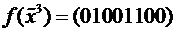 . Приведем несколько различных формул, являющихся д. н. ф. и реализующих функцию
. Приведем несколько различных формул, являющихся д. н. ф. и реализующих функцию 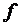 . Это ее СДНФ =
. Это ее СДНФ =  и д. н. ф.:
и д. н. ф.: 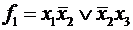 ,
, 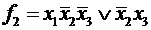 ,
, 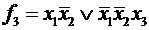 . Заметим, что
. Заметим, что  .
.
Лемма. Число различных д. н. ф. от переменных 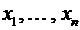 равно
равно 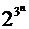 .
.
Доказательство. Действительно, число различных элементарных конъюнкций 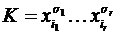 равно
равно 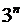 (“пустой” конъюнкции сопоставлена константа 1), так как для каждой переменной
(“пустой” конъюнкции сопоставлена константа 1), так как для каждой переменной  имеется три возможности: присутствует в конъюнкции, присутствует с отрицанием и отсутствует. Выпишем все элементарные конъюнкции, поставив между ними дизъюнкции:
имеется три возможности: присутствует в конъюнкции, присутствует с отрицанием и отсутствует. Выпишем все элементарные конъюнкции, поставив между ними дизъюнкции: 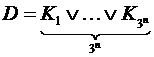 . Удаляя различные
. Удаляя различные 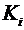 , получим все возможные д. н. ф. Следовательно, число различных д. н. ф. равно
, получим все возможные д. н. ф. Следовательно, число различных д. н. ф. равно 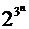 и одной функции соответствует несколько различных д. н. ф.
и одной функции соответствует несколько различных д. н. ф.
Индексом простоты (или сложностью) булевой функции называется функция 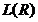 , определенная на множестве всех ДНФ и удовлетворяющая следующим свойствам:
, определенная на множестве всех ДНФ и удовлетворяющая следующим свойствам:
1) Свойство неотрицательности: 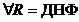
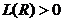 ;
;
2) Свойство монотонности: если  , где
, где 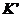 -элементарная конъюнкция,
-элементарная конъюнкция,  .
.
3) Свойство выпуклости: 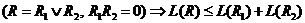
4) Свойство инвариантности: если ДНФ = 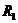 получена из ДНФ =
получена из ДНФ = 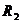 путем переименования переменных без отождествления, то
путем переименования переменных без отождествления, то 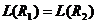 .
.
Виды индексов простоты:
1) 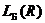 - число букв переменных, встречающихся в записи
- число букв переменных, встречающихся в записи 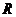 . Под буквой понимают символ переменной или ее отрицание, если переменная
. Под буквой понимают символ переменной или ее отрицание, если переменная  входит в формулу m раз, то говорят, что формула содержит m букв
входит в формулу m раз, то говорят, что формула содержит m букв  . Например в выражении
. Например в выражении 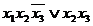 число переменных равно 3, а число букв равно 5, т.е. число букв равно числу вхождений переменных.
число переменных равно 3, а число букв равно 5, т.е. число букв равно числу вхождений переменных.
2) 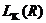 - число элементарных конъюнкций, входящих в
- число элементарных конъюнкций, входящих в 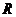 .
.
3) 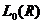 - число символов отрицаний, встречающихся в записи
- число символов отрицаний, встречающихся в записи 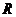 .
.
Каждый из указанных индексов удовлетворяет перечисленным свойствам.
Задача минимизации заданной логической функции сводится к представлению ее дизъюнктивной (или конъюнктивной) нормальной формой, имеющей наименьший индекс простоты. В качестве индекса простоты наиболее часто используется индекс 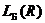 .
.
Пример 1. Пусть БФ задана вектором состояний 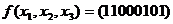 . Тогда для нее может быть записана СДНФ в виде
. Тогда для нее может быть записана СДНФ в виде  .
.
Эту функцию можно упростить
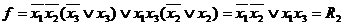
Вычислим индексы простоты для 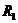 и
и 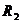 .
.
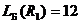 ,
, 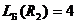 ;
;
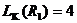 ,
,  ;
;
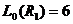 ,
, 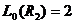 .
.
Следовательно, 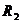 проще
проще 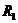 для всех трех индексов простоты.
для всех трех индексов простоты.
Пример 2. 
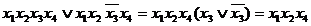
1 Построение сокращенной ДНФ с применением логических тождеств (методом Блейка).
Сокращенной д.н.ф. функции 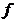 называется функция, которая содержит меньшее число букв, чем СДНФ. Если над СДНФ произвести все возможные операции склеивания, а затем все возможные операции поглощения то полученная функция будет иметь вид сокращенной ДНФ.
называется функция, которая содержит меньшее число букв, чем СДНФ. Если над СДНФ произвести все возможные операции склеивания, а затем все возможные операции поглощения то полученная функция будет иметь вид сокращенной ДНФ.
Если имеется некоторый конечный набор логических аргументов x 1, x 2, … xn, то логическое произведение любого их числа называется элементарным в том случае, когда сомножителями в нем являются либо одиночные аргументы, либо отрицания одиночных аргументов. Так, например, f 1 (х1, х2, x 3, х4) = х1 × х2 × x 3 × х4 — элементарное произведение (элементарная конъюнкция); 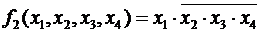 — не является элементарным произведением.
— не является элементарным произведением.
Cимвол любого аргумента в элементарной конъюнкции может встречаться только один раз, поскольку произведение аргумента самого на себя равно этому же аргументу, а произведение аргумента на свое отрицание равно нулю.
Далее под элементарными конъюнкциями мы будем иметь в виду правильные элементарные конъюнкции
Количество сомножителей в элементарной конъюнкции называется ее рангом.
Два элементарных произведения одинакового ранга r называются соседними, если они являются функциями одних и тех же аргументов и отличаются только знаком отрицания (инверсии) одного из сомножителей. Например, элементарные конъюнкции
f 1 (х1, х2, x 3, х4) = х1 × х2 × x 3 × х4 и f 3 (х1, х2, x 3, х4) = 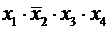
являются соседними, так как отличаются только одной инверсией в переменной x 2, а элементарные конъюнкции
f 3 (х1, х2, x 3, х4) = 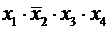 и f 4 (х1, х2, x 3, х4) =
и f 4 (х1, х2, x 3, х4) = 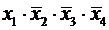
соседними не являются.
Правило склеивания для элементарных конъюнкций может быть сформулировано следующим образом: логическую сумму двух соседних произведений некоторого ранга r можно заменить одним элементарным произведением ранга r -1, являющимся общей частью исходных слагаемых.
Это правило является следствием распределительного закона 1-го рода и доказывается путем вынесения за скобку общей части слагаемых, являющихся соседними конъюнкциями. Тогда в скобках остается логическая сумма некоторого аргумента и его инверсии, равная единице, что и доказывает справедливость правила.
Например,
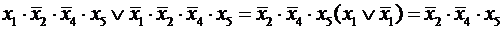 .
.
Поскольку алгебра логики является симметричной, то все определения, данные для конъюнкции, будут справедливы и для дизъюнкции.
Если имеется некоторый конечный набор логических аргументов, то логическая сумма (дизъюнкция), зависящая от любого их числа, называется элементарной в том случае, когда слагаемыми в ней являются либо одиночные аргументы, либо отрицания одиночных аргументов.
Далее под элементарными дизъюнкциями мы будем иметь в виду правильные элементарные дизъюнкции.
Количество слагаемых в элементарной дизъюнкции называется ее рангом. Две элементарные суммы одинакового ранга называются соседними, если они являются функциями одних и тех же аргументов и отличаются только знаком отрицания (инверсии) одного из слагаемых.
Правило склеивания двух элементарных дизъюнкций формулируется так: логическое произведение двух соседних сумм некоторого ранга r можно заменить одной элементарной суммой ранга r -1, являющейся общей частью исходных сомножителей.
Это правило является следствием распределительного закона 2-го рода и применяется для упрощения логических выражений.
Например:

Правило поглощения. Так же как и склеивание, поглощение может быть двух видов. Правило поглощения для двух элементарных конъюнкций формулируется так: логическую сумму двух элементарных произведений разных рангов, из которых одно является собственной частью другого, можно заменить слагаемым, имеющим меньший ранг.
Это правило является следствием распределительного закона 1-го рода. Доказывается оно посредством вынесения за скобку общей части слагаемых. В скобках останется логическая сумма некоторого выражения и единицы, равная в свою очередь также единице, что и доказывает справедливость правила. Например,

Правило поглощения для двух элементарных дизъюнкций: логическое произведение двух элементарных сумм разных рангов, из которых одна является общей частью другой, можно заменить сомножителем, имеющим меньший ранг.
Это правило является следствием распределительного закона 2-го рода и также находит широкое применение для упрощения логических функций.
Правило развертывания. Это правило регламентирует действие, обратное склеиванию. Иногда требуется представить некоторое логическое выражение в виде совокупности конституент единицы или конституент нуля. Если членами преобразуемого выражения являются элементарные конъюнкции, то переход от них к конституентам единицы производится в три этапа по следующему правилу:
· в развертываемую элементарную конъюнкцию ранга r в качестве дополнительных сомножителей вводится п- r единиц, где п — ранг конституенты;
· каждая единица представляется в виде логической суммы некоторой, не имеющейся в исходной конъюнкции переменной и ее отрицания:  ;
;
· производится раскрытие всех скобок на основе распределительного закона первого рода, что приводит к развертыванию исходной элементарной конъюнкции ранга r в логическую сумму кон-ституент единицы.
Пример 5.1. Развернуть элементарную конъюнкцию f(x1,x2,x3,x4) = = x 1 × x 3 в логическую сумму конституент единицы.
Решение. Ранг конституенты единицы для данной функции равен 4. Производим развертывание исходной конъюнкции поэтапно в соответствии с правилом развертывания:
1-й этап— f (x 1, x 2, x 3, x 4) = x 1 × 1 × x 3 × 1.
2-й этап — f (x 1, x 2, x 3, x 4) = 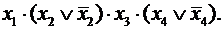
3-й этап — f (x 1, x 2, x 3, x 4)=
= 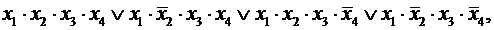 что и требовалось получить.
что и требовалось получить.
Если членами преобразуемого выражения являются элементарные дизъюнкции, то переход от них к конституентам нуля производится также в три этапа по следующему правилу:
· в развертываемую элементарную дизъюнкцию ранга r в качестве дополнительных слагаемых вводится п-r нулей;
· каждый нуль представляется в виде логического произведения некоторой, не имеющейся в исходной дизъюнкции переменной, и ее отрицания: 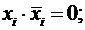
· получившееся выражение преобразуется на основе распределительного закона второго рода таким образом, чтобы произвести развертывание исходной элементарной дизъюнкции ранга r в логическое произведение конституент нуля.
Пример 5.2. Развернуть элементарную дизъюнкцию f (x 1, x 2, x 3, x 4)= =x3 Ú x4 влогическое произведение конституент нуля.
Решение. Ранг конституенты нуля п = 4. Далее производим развертывание исходной дизъюнкции поэтапно в соответствии с правилом развертывания:
1-й этап — f (x 1, x 2, x 3, x 4) =0 Ú 0 Ú x3 Ú x4;
2-й этап — f (x 1, x 2, x 3, x 4) = 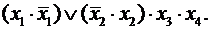
3-йэтап— f (x 1, x 2, x 3, x 4)=
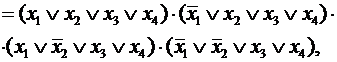
что и требовалось получить.
Проверить правильность проведенных преобразований можно при помощи правила склеивания.
В основе использования метода Блейка лежат операции склеивания и операции поглощения.
1)Законы поглощения:
1.1) 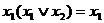 ,
, 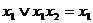
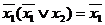
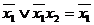
1.2) 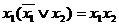 ,
, 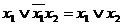
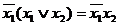 ,
, 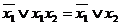
Отметим, что формулы во втором столбце получаются из формул первого столбца с помощью принципа двойственности.
2) Закон склеивания (объединения конъюнкций):
2.1) 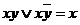 .
.
2.2) Закон обобщенного склеивания: 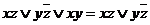 .
.
Пример. Получить сокращенную ДНФ методом Блейка
1) 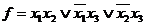 .
.

2 Матричный метод Карно. 
Матричный метод основан на некоторых геометрических построениях. Соотношение между двоичными переменными можно представить в наглядной геометрической форме.
Рассмотрим логическую функцию двух переменных. Все четыре конъюнкции двух двоичных переменных (члены СДНФ) могут быть изображены на плоскости в виде точек с координатами 00,01,10,11, где первая цифра соответствует переменной  , а вторая – переменной
, а вторая – переменной  . Эти точки можно соединить линиями и полученный в результате квадрат будет наглядно изображать члены СДНФ двух переменных.
. Эти точки можно соединить линиями и полученный в результате квадрат будет наглядно изображать члены СДНФ двух переменных.

Координаты вершин квадрата, выраженные двоичными числами, соответствуют двоичным номерам конъюнкций.: 00 сответствует 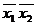 , 01 -
, 01 - 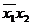 , 10 -, 11 -
, 10 -, 11 - 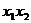 . Координаты соседних вершин отличаются только одним двоичным знаком и, следовательно, минтермы, соответствующие этим числам, отличаются только одной переменной. Если объединить члены, соответствующие двум различным вершинам, то эта переменная будет исключена. Например, сложив минтермы
. Координаты соседних вершин отличаются только одним двоичным знаком и, следовательно, минтермы, соответствующие этим числам, отличаются только одной переменной. Если объединить члены, соответствующие двум различным вершинам, то эта переменная будет исключена. Например, сложив минтермы 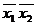 и
и 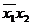 , изображаемые вершинами 00 и 01, получим
, изображаемые вершинами 00 и 01, получим 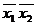
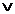
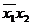 =
= 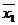 . Ту же операцию исключения переменной можно выполнить, сравнивая непосредственно два двоичных числа 00 и 01.В первом разряде двоичные знаки у обоих чисел одинаковы, поэтому в объединении ставим 0, во втором разряде знаки различны, поэтому во втором разряде ставим черту.
. Ту же операцию исключения переменной можно выполнить, сравнивая непосредственно два двоичных числа 00 и 01.В первом разряде двоичные знаки у обоих чисел одинаковы, поэтому в объединении ставим 0, во втором разряде знаки различны, поэтому во втором разряде ставим черту.
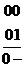
Число 0 соответствует переменной 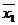 . Черта указывает, что исключена переменная
. Черта указывает, что исключена переменная  . Следовательно, если два двоичных числа отличаются двоичными цифрами только в одном разряде, то их можно заменить двоичным числом, у которого в этом разряде можно поставить черточку. Черточка указывает номер исключенной переменной. Линия, соединяющая вершины 00 и 01 может быть названа линией
. Следовательно, если два двоичных числа отличаются двоичными цифрами только в одном разряде, то их можно заменить двоичным числом, у которого в этом разряде можно поставить черточку. Черточка указывает номер исключенной переменной. Линия, соединяющая вершины 00 и 01 может быть названа линией 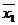 .
.
Геометрической моделью функции трех переменных может служить трехмерный куб, вершины которого соответствуют членам СДНФ. Координаты соседних вершин отличаются, как и в случае плоской модели, только одним двоичным знаком, а соответствующие члены только одной переменной. Вследствие этого линии, соединяющие соседние вершины куба можно обозначить двумя переменными, которые на этой линии не меняют свое значение, а грани куба – одной переменной.
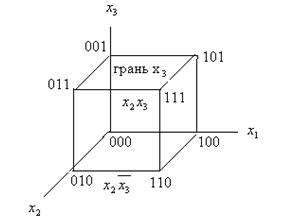
Соединение двух соседних вершин линией позволяет исключить одну переменную, причем это исключение можно выполнить, сравнив двоичные обозначения вершин. Например, сравнивая 011 и 111, получим  , что соответствует операции сложения конъюнкций
, что соответствует операции сложения конъюнкций 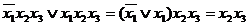
Точно также соединение линиями 4 вершин, лежащих на одной грани, позволяет исключить две переменные. Действительно, сравнив 011 с 111 и 001 с 101, получим

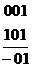
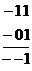
Вначале была исключена переменная  , а затем переменная
, а затем переменная  .
.
В результате осталась одна переменная 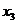 .
.
Для функции четырех переменных геометрической моделью является четырехмерный куб. Однако изобразить его на плоскости невозможно и использовать для минимизации сложно. Более удобной для минимизации является карта Карно. Карта Карно построена так, что два соседних столбца (строки) отличаются одним знаком. Любая конъюнкция четырех переменных изображается на карте одной клеткой, находящейся на пересечении строки и столбца, обозначения которых образуют двоичный номер конъюнкции. Конъюнкции, соответствующие соседним клеткам, отличаются только одной переменной. Соседними на карте Карно являются не только клетки, находящиеся внутри карты, но и на концах каждой строки и каждого столбца. Любая функция может быть задана на матрице единицами в клетках, соответствующих входящим в СДНФ конъюнкциям – минтермам, и нулями в остальных клетках, которые можно не записывать. Например, функция 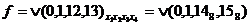 имеет единицы в клетках 0000, 0001,1100, 1101. Четыре минтерма можно сгруппировать по два, объединив для этого соседние минтермы. Объединенные минтермы обводятся замкнутыми линиями. В результате функция приводится к сумме двух конъюнкций трех переменных.
имеет единицы в клетках 0000, 0001,1100, 1101. Четыре минтерма можно сгруппировать по два, объединив для этого соседние минтермы. Объединенные минтермы обводятся замкнутыми линиями. В результате функция приводится к сумме двух конъюнкций трех переменных.


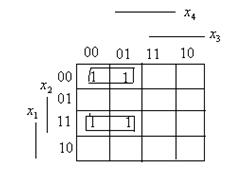
В результате минимизации получим функцию
 .
.
Преобразования, выполненные на карте Карно, соответствуют следующим алгебраическим преобразованиям
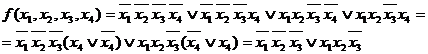 Будем называть конфигурации, образованные соседними заполненными клетками, подквадратами. Подквадрат – набор клеток, в которых одна или несколько переменных имеют постоянное значение. Так, по карте четырех переменных для двухклеточного квадрата характерно то, что в нем три переменные постоянны, а четвертая принимает оба своих значения. Для четырехклеточного подквадрата постоянны две переменные, а две другие принимают все четыре возможные комбинации значений. Объединяя две соседние клетки, мы тем самым будем исключать одну переменную, объединяя четыре соседних клетки, исключаем две переменных, объединяя восемь соседних клеток, - исключаем три переменных. (Это справедливо в том случае, когда форма подквадрата является прямоугольной или квадратной). В подквадраты можно объединять клетки, находящиеся на разных концах строки или столбца.
Будем называть конфигурации, образованные соседними заполненными клетками, подквадратами. Подквадрат – набор клеток, в которых одна или несколько переменных имеют постоянное значение. Так, по карте четырех переменных для двухклеточного квадрата характерно то, что в нем три переменные постоянны, а четвертая принимает оба своих значения. Для четырехклеточного подквадрата постоянны две переменные, а две другие принимают все четыре возможные комбинации значений. Объединяя две соседние клетки, мы тем самым будем исключать одну переменную, объединяя четыре соседних клетки, исключаем две переменных, объединяя восемь соседних клеток, - исключаем три переменных. (Это справедливо в том случае, когда форма подквадрата является прямоугольной или квадратной). В подквадраты можно объединять клетки, находящиеся на разных концах строки или столбца.
Карта Карно строится в соответствии с таблицей истинности логической функции. Столбцы и строки карты Карно обозначаются прямыми и инверсными переменными данной функции.
Рис 4.3.1. Карта Карно для 2-х и для 3-х переменных 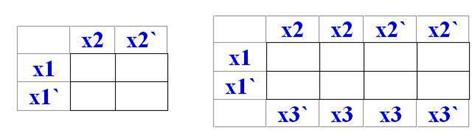
Число клеток карты равно числу всех возможных комбинаций входных переменных, т.е. 2ⁿ, где n - чило входных переменных. Это также значит, что число клеток карты равно максимальному числу минтерм СНДФ.
Каждая клетка карты соответствует логическому произведению (прямого или инверсного значения) переменных, на пересечении которых она находится, что соответствует минтерме СНДФ. В карту Карно заносятся соответствующие значения минтерм.
Строки и столбцы карты обозначаются таким образом, чтобы любые соседние клетки по строкам или по столбцам отличались бы между собой значением только одной переменной. Такое обозначение соответствует последовательности чисел в коде Грея. Это сделано для того, чтобы было бы возможно применить закон склеивания.
Клетки, находящиеся на границах одной строки или столбца, так же считаются соседними.
Рис. 4.3.2. Карта Карно строится на основании таблицы истинности
| a
| b
| c
| f
|
| 0
| 0
| 0
| а`b`c`
|
| 1
| 0
| 0
| ab`c`
|
| 0
| 1
| 0
| a`bc`
|
| 0
| 0
| 1
| a`b`c
|
| 1
| 1
| 0
| abc`
|
| 1
| 0
| 1
| ab`c
|
| 0
| 1
| 1
| a`bc
|
| 1
| 1
| 1
| abc
|
Каждая клетка карты соответствует произведению переменных, на пересечении которых она находится.
Рис. 4.3.3. Принцип составления карты Карно

Для минимизации функций используется закон «склеивания»:
ab + ab` = a
Если переменная (аргумент) изменяет свое значение, а функция при этом остается неизменной, то эту переменную можно исключить из выражения.
Правило минимизации.
Для получения минимальной функции НДФ (или МНДФ) охватывают областями все клетки, имеющие значение 1 и являющиеся соседними. Эти области должны быть прямоугольной формы и содержать чётное количество клеток. Для каждой области записывается неизменяющаяся часть объедененных минтерм. При этом минимизируемые области могут иметь общие минтермы (пересекаться). В заключение все минтермы суммируются.

Рис. 4.3.4. Пример минимизации трех переменных с помощью карты Карно
В данном примере, произведения, образующие квадрат (с учётом замкнутости краевых линий диаграммы), позволяют исключить из общего выражения две переменные. При этом количество минтерм также сократилось.

Рис. 4.3.5. Метод скручивания карты Карно
Крайние квадраты карты являются соседними при ее скручивании. Это значит, что они тоже подлежат минимизации. На плоскости можно изобразить карту Карно для 4-х переменных. Для 5 и более переменных необходимы объемные фигуры.
 Пример
Пример
Допустим, что задана логическая функция с помощью таблицы истинности.
Рис. 4.3.6. Пример создания логической функции

Составим карту Карно, объеденим единицы и получим минимальную форму функции.
Рис. 4.3.7. Пример минимизации

Переменная х изменяется, и поэтому её можно упустить!





 Пример
Пример

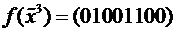 . Приведем несколько различных формул, являющихся д. н. ф. и реализующих функцию
. Приведем несколько различных формул, являющихся д. н. ф. и реализующих функцию 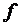 . Это ее СДНФ =
. Это ее СДНФ =  и д. н. ф.:
и д. н. ф.: 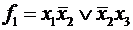 ,
, 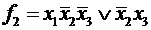 ,
, 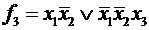 . Заметим, что
. Заметим, что  .
.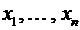 равно
равно 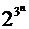 .
.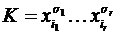 равно
равно 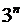 (“пустой” конъюнкции сопоставлена константа 1), так как для каждой переменной
(“пустой” конъюнкции сопоставлена константа 1), так как для каждой переменной  имеется три возможности: присутствует в конъюнкции, присутствует с отрицанием и отсутствует. Выпишем все элементарные конъюнкции, поставив между ними дизъюнкции:
имеется три возможности: присутствует в конъюнкции, присутствует с отрицанием и отсутствует. Выпишем все элементарные конъюнкции, поставив между ними дизъюнкции: 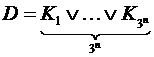 . Удаляя различные
. Удаляя различные 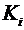 , получим все возможные д. н. ф. Следовательно, число различных д. н. ф. равно
, получим все возможные д. н. ф. Следовательно, число различных д. н. ф. равно 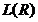 , определенная на множестве всех ДНФ и удовлетворяющая следующим свойствам:
, определенная на множестве всех ДНФ и удовлетворяющая следующим свойствам: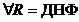
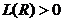 ;
; , где
, где 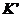 -элементарная конъюнкция,
-элементарная конъюнкция,  .
.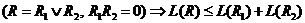
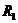 получена из ДНФ =
получена из ДНФ = 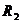 путем переименования переменных без отождествления, то
путем переименования переменных без отождествления, то 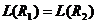 .
.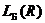 - число букв переменных, встречающихся в записи
- число букв переменных, встречающихся в записи 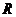 . Под буквой понимают символ переменной или ее отрицание, если переменная
. Под буквой понимают символ переменной или ее отрицание, если переменная  входит в формулу m раз, то говорят, что формула содержит m букв
входит в формулу m раз, то говорят, что формула содержит m букв 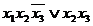 число переменных равно 3, а число букв равно 5, т.е. число букв равно числу вхождений переменных.
число переменных равно 3, а число букв равно 5, т.е. число букв равно числу вхождений переменных.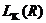 - число элементарных конъюнкций, входящих в
- число элементарных конъюнкций, входящих в 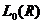 - число символов отрицаний, встречающихся в записи
- число символов отрицаний, встречающихся в записи 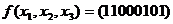 . Тогда для нее может быть записана СДНФ в виде
. Тогда для нее может быть записана СДНФ в виде  .
.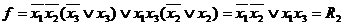
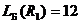 ,
, 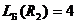 ;
;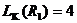 ,
,  ;
;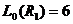 ,
, 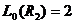 .
.
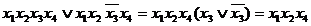
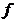 называется функция, которая содержит меньшее число букв, чем СДНФ. Если над СДНФ произвести все возможные операции склеивания, а затем все возможные операции поглощения то полученная функция будет иметь вид сокращенной ДНФ.
называется функция, которая содержит меньшее число букв, чем СДНФ. Если над СДНФ произвести все возможные операции склеивания, а затем все возможные операции поглощения то полученная функция будет иметь вид сокращенной ДНФ.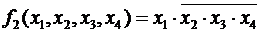 — не является элементарным произведением.
— не является элементарным произведением.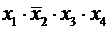
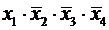
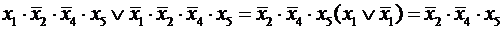 .
.

 ;
;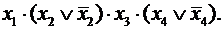
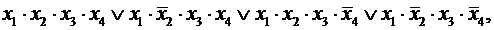 что и требовалось получить.
что и требовалось получить.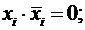
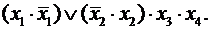
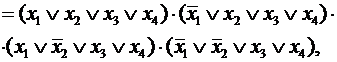
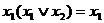 ,
, 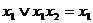
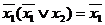
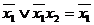
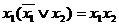 ,
, 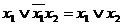
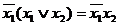 ,
, 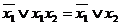
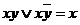 .
.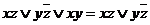 .
.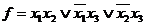 .
.
 . Эти точки можно соединить линиями и полученный в результате квадрат будет наглядно изображать члены СДНФ двух переменных.
. Эти точки можно соединить линиями и полученный в результате квадрат будет наглядно изображать члены СДНФ двух переменных.
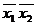 , 01 -
, 01 - 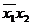 , 10 -, 11 -
, 10 -, 11 - 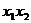 . Координаты соседних вершин отличаются только одним двоичным знаком и, следовательно, минтермы, соответствующие этим числам, отличаются только одной переменной. Если объединить члены, соответствующие двум различным вершинам, то эта переменная будет исключена. Например, сложив минтермы
. Координаты соседних вершин отличаются только одним двоичным знаком и, следовательно, минтермы, соответствующие этим числам, отличаются только одной переменной. Если объединить члены, соответствующие двум различным вершинам, то эта переменная будет исключена. Например, сложив минтермы 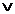
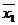 . Ту же операцию исключения переменной можно выполнить, сравнивая непосредственно два двоичных числа 00 и 01.В первом разряде двоичные знаки у обоих чисел одинаковы, поэтому в объединении ставим 0, во втором разряде знаки различны, поэтому во втором разряде ставим черту.
. Ту же операцию исключения переменной можно выполнить, сравнивая непосредственно два двоичных числа 00 и 01.В первом разряде двоичные знаки у обоих чисел одинаковы, поэтому в объединении ставим 0, во втором разряде знаки различны, поэтому во втором разряде ставим черту.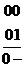

 , что соответствует операции сложения конъюнкций
, что соответствует операции сложения конъюнкций 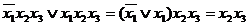
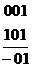
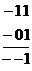
 .
.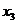 .
.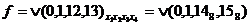 имеет единицы в клетках 0000, 0001,1100, 1101. Четыре минтерма можно сгруппировать по два, объединив для этого соседние минтермы. Объединенные минтермы обводятся замкнутыми линиями. В результате функция приводится к сумме двух конъюнкций трех переменных.
имеет единицы в клетках 0000, 0001,1100, 1101. Четыре минтерма можно сгруппировать по два, объединив для этого соседние минтермы. Объединенные минтермы обводятся замкнутыми линиями. В результате функция приводится к сумме двух конъюнкций трех переменных.


 .
.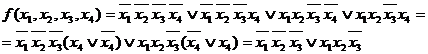 Будем называть конфигурации, образованные соседними заполненными клетками, подквадратами. Подквадрат – набор клеток, в которых одна или несколько переменных имеют постоянное значение. Так, по карте четырех переменных для двухклеточного квадрата характерно то, что в нем три переменные постоянны, а четвертая принимает оба своих значения. Для четырехклеточного подквадрата постоянны две переменные, а две другие принимают все четыре возможные комбинации значений. Объединяя две соседние клетки, мы тем самым будем исключать одну переменную, объединяя четыре соседних клетки, исключаем две переменных, объединяя восемь соседних клеток, - исключаем три переменных. (Это справедливо в том случае, когда форма подквадрата является прямоугольной или квадратной). В подквадраты можно объединять клетки, находящиеся на разных концах строки или столбца.
Будем называть конфигурации, образованные соседними заполненными клетками, подквадратами. Подквадрат – набор клеток, в которых одна или несколько переменных имеют постоянное значение. Так, по карте четырех переменных для двухклеточного квадрата характерно то, что в нем три переменные постоянны, а четвертая принимает оба своих значения. Для четырехклеточного подквадрата постоянны две переменные, а две другие принимают все четыре возможные комбинации значений. Объединяя две соседние клетки, мы тем самым будем исключать одну переменную, объединяя четыре соседних клетки, исключаем две переменных, объединяя восемь соседних клеток, - исключаем три переменных. (Это справедливо в том случае, когда форма подквадрата является прямоугольной или квадратной). В подквадраты можно объединять клетки, находящиеся на разных концах строки или столбца.




