Направлен вектор 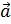 в сторону вогнутости траектории в соприкасающейся плоскости, т.к. в пределе точка
в сторону вогнутости траектории в соприкасающейся плоскости, т.к. в пределе точка 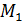 стремиться к точке М.
стремиться к точке М.
Размерность ускорения в системе СИ, м/с2.
4. Скорость и ускорение точки при координатном способе задания движения
Для определения скорости точки спроектируем векторное уравнение (5.4) на координатные оси, получим:
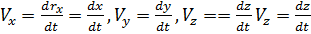 . (5.6)
. (5.6)
Проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.
Модуль скорости через ее проекции на координатные оси
 . (5.7)
. (5.7)
Направление скорости найдем по направляющим косинусам
 . (5.8)
. (5.8)
Ускорение точки определяется аналогично скорости из уравнения (5.5).
Проекции ускорений на координатные оси
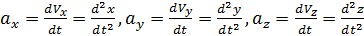 . (5.9)
. (5.9)
Проекции ускорений на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени.
Модуль ускорения
 . (5.10)
. (5.10)
Направление ускорения
 . (5.11)
. (5.11)
Скорости и ускорения при естественном задании движения точки
При естественном способе задания движения точки траектория известна, поэтому в качестве системы отсчета принимается не произвольная Oxyz декартова система координат (в которой траекторию надо определять и строить), а оси естественного (скоростного) трехгранника 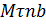 , которые перемещаются вместе с движущейся точкой. Ось
, которые перемещаются вместе с движущейся точкой. Ось 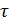 направлена по касательной к траектории в сторону положительного отсчета расстояния; ось n - по нормали к траектории в соприкасающейся плоскости (в плоскости кривой, если кривая плоская); ось b - перпендикулярна к первым двум. Эти оси называются: касательная, главная нормаль, бинормаль.
направлена по касательной к траектории в сторону положительного отсчета расстояния; ось n - по нормали к траектории в соприкасающейся плоскости (в плоскости кривой, если кривая плоская); ось b - перпендикулярна к первым двум. Эти оси называются: касательная, главная нормаль, бинормаль.
Скорость точки направлена по касательной к траектории и определяется только одной проекцией  , на ось
, на ось  . Следовательно,
. Следовательно,  совпадает по модулю с V и может отличаться знаком минус (при замедленном движении).
совпадает по модулю с V и может отличаться знаком минус (при замедленном движении).
Найдем ее значение. Пусть за промежуток времени 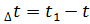 тело совершит перемещение по траектории
тело совершит перемещение по траектории 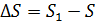 (рис. 5.2). Тогда средняя скорость
(рис. 5.2). Тогда средняя скорость  и в пределе получим
и в пределе получим
 . (5.12)
. (5.12)
Скорость точки в данный момент времени равна первой производной от криволинейной координаты S по времени.
Ускорение точки при естественном способе задания движения определяется через проекции на оси τ и n. Проекции ускорения на бинормаль 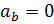 , т.к. вектор ускорения лежит в соприкасающейся плоскости. Из §24 вектор ускорения
, т.к. вектор ускорения лежит в соприкасающейся плоскости. Из §24 вектор ускорения
 .
.
В проекциях на оси τ и n получим (рис. 5.5):
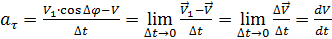 ,
,
так как  .
.
 ,
,
так как  .
.
Окончательно, с учетом уравнения (5.12), будем иметь:
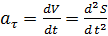 . (5.13)
. (5.13)
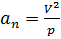 . (5.14)
. (5.14)
Проекция ускорения на касательную ось (касательное ускорение) равна первой производной от скорости или второй производной от криволинейной координаты по времени. Проекция ускорения на главную нормаль (нормальное ускорение) равно квадрату скорости, деленному на радиус кривизны траектории.
На рис. 5.6 изображены векторы 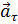 и
и 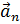 . Вектор
. Вектор 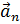 по величине из уравнения (5.14) всегда положителен и направлен по главной нормали в сторону вогнутости кривой.
по величине из уравнения (5.14) всегда положителен и направлен по главной нормали в сторону вогнутости кривой.



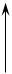


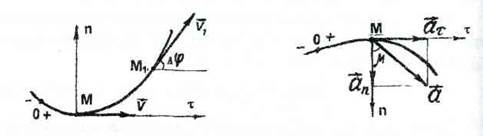
Рис. 5.5 Рис. 5.6
Вектор 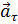 может быть и положительным и отрицательным в зависимости от знака проекции (уравнение 5.13). Из рис. 5.6 видно, что
может быть и положительным и отрицательным в зависимости от знака проекции (уравнение 5.13). Из рис. 5.6 видно, что 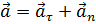 , т.е. полное ускорение точки определяется диагональю параллелограмма, стороны которого
, т.е. полное ускорение точки определяется диагональю параллелограмма, стороны которого 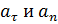 .
.
По величине ускорение точки
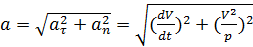 . (5.15)
. (5.15)
Направление вектора к нормали определяется углом µ.:
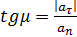 . (5.16)
. (5.16)
Домашнее задание:
1. Прочитайте конспект
2. Запишите способы задания движения точки
3. Определение скорости и ускорения при разных способах задания движения точки



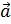 в сторону вогнутости траектории в соприкасающейся плоскости, т.к. в пределе точка
в сторону вогнутости траектории в соприкасающейся плоскости, т.к. в пределе точка 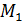 стремиться к точке М.
стремиться к точке М.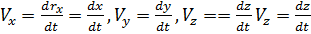 . (5.6)
. (5.6) . (5.7)
. (5.7) . (5.8)
. (5.8)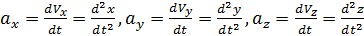 . (5.9)
. (5.9) . (5.10)
. (5.10) . (5.11)
. (5.11)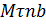 , которые перемещаются вместе с движущейся точкой. Ось
, которые перемещаются вместе с движущейся точкой. Ось 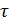 направлена по касательной к траектории в сторону положительного отсчета расстояния; ось n - по нормали к траектории в соприкасающейся плоскости (в плоскости кривой, если кривая плоская); ось b - перпендикулярна к первым двум. Эти оси называются: касательная, главная нормаль, бинормаль.
направлена по касательной к траектории в сторону положительного отсчета расстояния; ось n - по нормали к траектории в соприкасающейся плоскости (в плоскости кривой, если кривая плоская); ось b - перпендикулярна к первым двум. Эти оси называются: касательная, главная нормаль, бинормаль. , на ось
, на ось  . Следовательно,
. Следовательно, 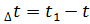 тело совершит перемещение по траектории
тело совершит перемещение по траектории 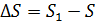 (рис. 5.2). Тогда средняя скорость
(рис. 5.2). Тогда средняя скорость  и в пределе получим
и в пределе получим . (5.12)
. (5.12)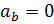 , т.к. вектор ускорения лежит в соприкасающейся плоскости. Из §24 вектор ускорения
, т.к. вектор ускорения лежит в соприкасающейся плоскости. Из §24 вектор ускорения .
.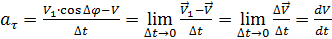 ,
, .
. ,
, .
.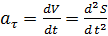 . (5.13)
. (5.13)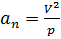 . (5.14)
. (5.14)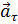 и
и 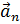 . Вектор
. Вектор 


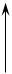


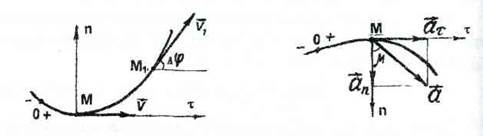
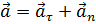 , т.е. полное ускорение точки определяется диагональю параллелограмма, стороны которого
, т.е. полное ускорение точки определяется диагональю параллелограмма, стороны которого 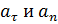 .
.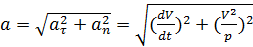 . (5.15)
. (5.15)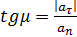 . (5.16)
. (5.16)

