Используя ранее полученные формулу дифференцирования для функций первой, второй и третьей степеней:
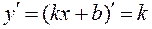
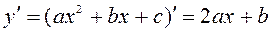
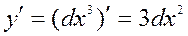
для аргумента в первой, во второй и в третьей степени мы можем получить следующее:
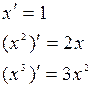
Применяя метод математической индукции, формула производной степенной функции будет выглядеть следующим образом:

Приняв  и
и 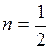 , получаются следующие формулы:
, получаются следующие формулы:
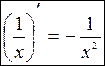 и
и 
Формула дифференцирования показательной функции
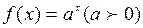
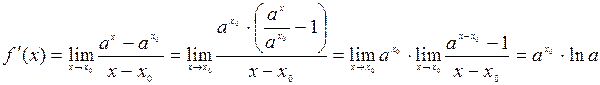
(Использовался известный предел 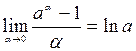 )
)
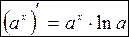
В случае 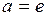 , применяя определение натурального логарифма, для числа е получаем формулу:
, применяя определение натурального логарифма, для числа е получаем формулу:

Формула дифференцирования тригонометрических функций
А) синуса
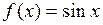
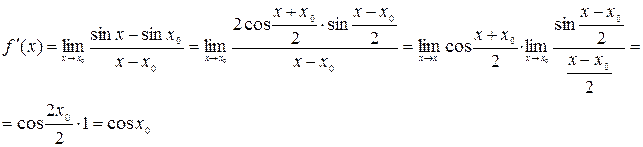
(применялась формула разности синусов и использовался первый замечательный предел: 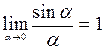 )
)
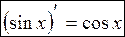
Б) косинуса
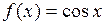
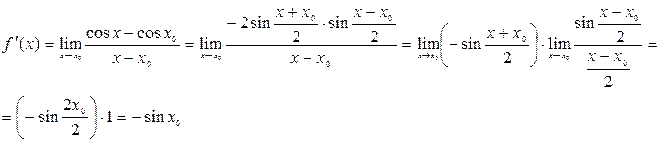
(применялась формула разности косинусов и использовался первый замечательный предел: 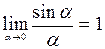 )
)
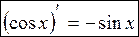
В) тангенса
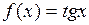 ,
, 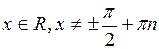
По определению, 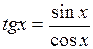 . Воспользуемся формулой производной частного функций и основным тригонометрическим тождеством:
. Воспользуемся формулой производной частного функций и основным тригонометрическим тождеством:
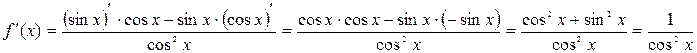
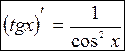
Г) котангенса
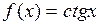 ,
, 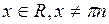
По определению, 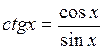 . Воспользуемся формулой производной частного функций и основным тригонометрическим тождеством:
. Воспользуемся формулой производной частного функций и основным тригонометрическим тождеством:
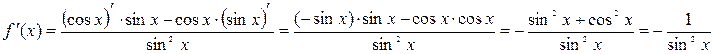
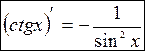
Для нахождения производных логарифмической и обратных тригонометрических функций понадобится теорема о производной обратной функции, так как данные функции являются обратными к показательной и тригонометрическим функциям соответственно.
Производная обратной функции
Теорема. Если функция 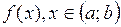 , и ее обратная функция
, и ее обратная функция 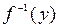 имеют производные, то
имеют производные, то 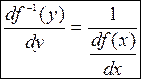 .
.
Опуская значение аргументов, получаем 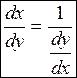 или
или 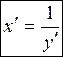 .
.
Формула дифференцирования логарифмической функции
Функция 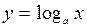 , где
, где 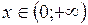 является обратной к функции
является обратной к функции 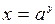 .
.
Используя формулу производной обратной функции, будем иметь:
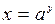 ,
, 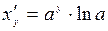
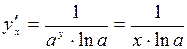 .
.
Итак,  . В частности,
. В частности, 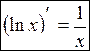 .
.
Формулы дифференцирования обратных тригонометрических функций
А) арксинуса
Функция 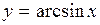 ,
, 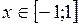 , является обратной к функции
, является обратной к функции 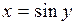 ,
, 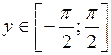 .
.
По правилу дифференцирования обратной функции
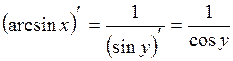 .
.
Выразим 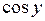 через
через 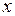 :
:
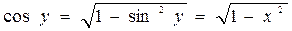 .
.
Под корнем следует брать знак «+», потому что 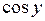 на промежутке
на промежутке 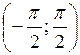 положителен.
положителен.
Таким образом,

Б) арккосинуса
Функция 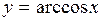 ,
, 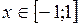 , является обратной к функции
, является обратной к функции 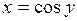 ,
, 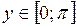 .
.
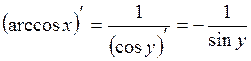
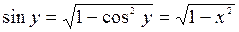
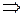
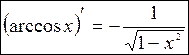
В) арктангенса
Функция 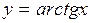 ,
, 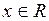 , является обратной к функции
, является обратной к функции 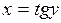 ,
, 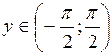 .
.
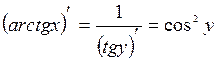
Используя основное тригонометрическое тождество, получаем следующее:
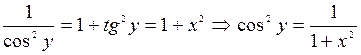
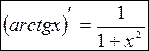
Г) арккотангенса
Функция 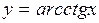 ,
, 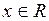 , является обратной к функции
, является обратной к функции 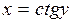 ,
, 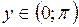 .
.
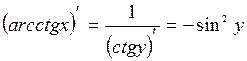
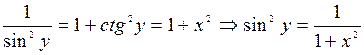
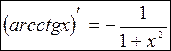
Сложная функция и ее производная
Если переменная 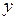 зависит от переменной
зависит от переменной 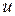 , а переменная
, а переменная 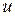 , в свою очередь, зависит от переменной
, в свою очередь, зависит от переменной 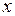 , то есть
, то есть 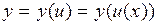 , то
, то 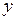 называют сложной функцией. При этом
называют сложной функцией. При этом 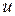 называют промежуточным аргументом, а
называют промежуточным аргументом, а 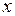 – окончательным аргументом (иногда
– окончательным аргументом (иногда 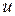 называют внутренней функцией, а
называют внутренней функцией, а 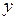 - внешней функцией).
- внешней функцией).
Составление сложной функции из двух функций называют суперпозицие й этих функций.



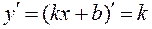
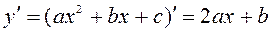
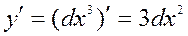
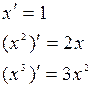

 и
и 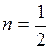 , получаются следующие формулы:
, получаются следующие формулы: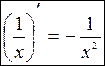 и
и 
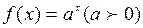
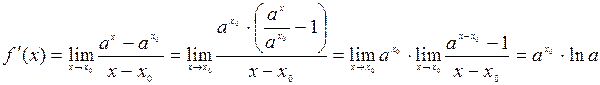
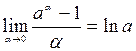 )
)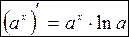
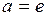 , применяя определение натурального логарифма, для числа е получаем формулу:
, применяя определение натурального логарифма, для числа е получаем формулу:
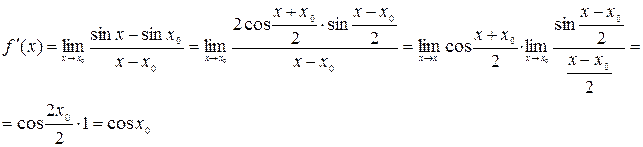
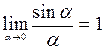 )
)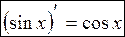
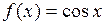
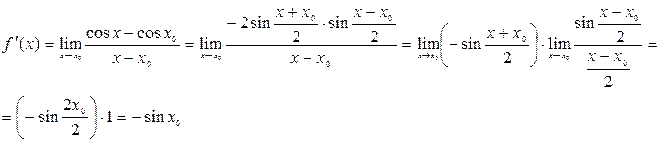
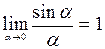 )
)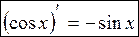
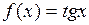 ,
, 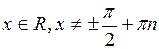
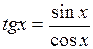 . Воспользуемся формулой производной частного функций и основным тригонометрическим тождеством:
. Воспользуемся формулой производной частного функций и основным тригонометрическим тождеством: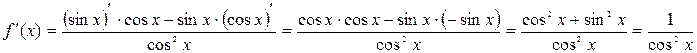
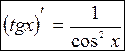
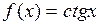 ,
, 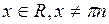
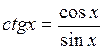 . Воспользуемся формулой производной частного функций и основным тригонометрическим тождеством:
. Воспользуемся формулой производной частного функций и основным тригонометрическим тождеством: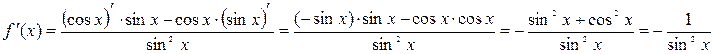
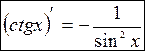
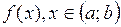 , и ее обратная функция
, и ее обратная функция 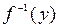 имеют производные, то
имеют производные, то 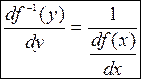 .
.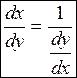 или
или 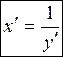 .
.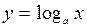 , где
, где 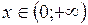 является обратной к функции
является обратной к функции 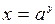 .
.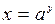 ,
, 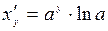
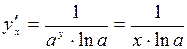 .
. . В частности,
. В частности, 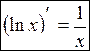 .
.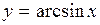 ,
, 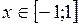 , является обратной к функции
, является обратной к функции 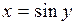 ,
, 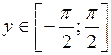 .
.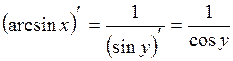 .
.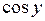 через
через  :
: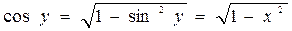 .
.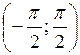 положителен.
положителен.
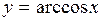 ,
, 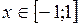 , является обратной к функции
, является обратной к функции 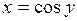 ,
, 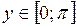 .
.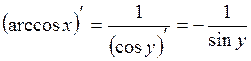
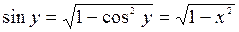
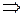
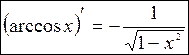
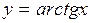 ,
, 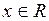 , является обратной к функции
, является обратной к функции 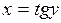 ,
, 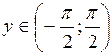 .
.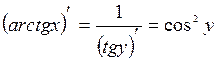
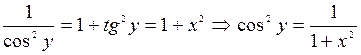
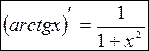
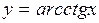 ,
, 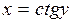 ,
, 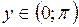 .
.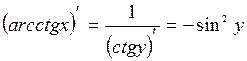
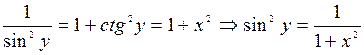
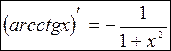
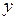 зависит от переменной
зависит от переменной 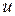 , а переменная
, а переменная 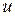 , в свою очередь, зависит от переменной
, в свою очередь, зависит от переменной 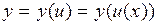 , то
, то 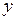 называют сложной функцией. При этом
называют сложной функцией. При этом 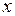 – окончательным аргументом (иногда
– окончательным аргументом (иногда 


