§1. Собственные интегралы, зависящие от параметра
1. Непрерывность интеграла от параметра
Рассмотрим интеграл
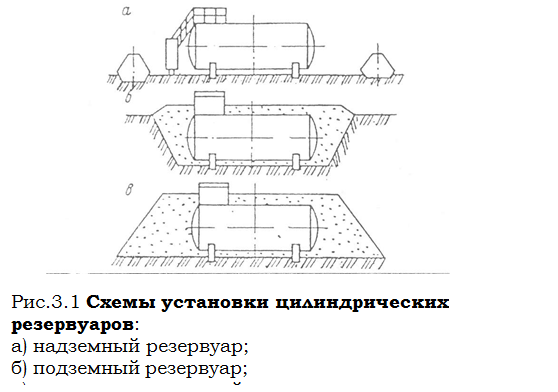
F (y) = 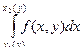
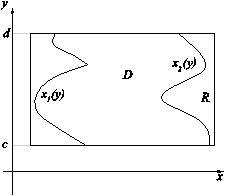
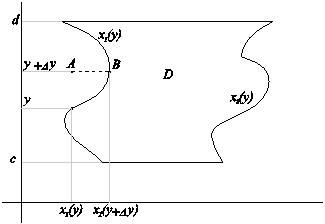
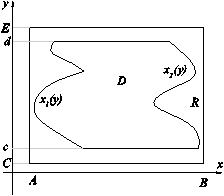
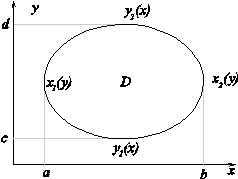
для области вида типа B, D ={(x, y): x 1 (y) £ x £ x 2 (y), y Î [ c, d ]}
Предполагается, что f определена в некоторой прямоугольной области R, содержащей D, как показано на рисунке (D - замкнутая ), x 1 (y), x 2 (y) непрерывные функции, определенные на [ c, d ].
Теорема. Если f непрерывна на R, x 1 (y), x 2 (y) непрерывны на [ c, d ], то F (y) непрерывна на [ c, d ].
Доказательство. Для заданного 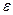 , используя равномерную непрерывность функции f можно подобрать D y так, что
, используя равномерную непрерывность функции f можно подобрать D y так, что
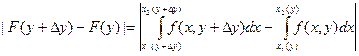 =
=  £
£ 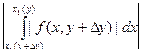 +
+ 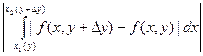 +
+ 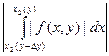 £ M|x1(y+ D y)-x1(y)|+(b - a) e + M| x2(y+ D y)-x2(y)|.
£ M|x1(y+ D y)-x1(y)|+(b - a) e + M| x2(y+ D y)-x2(y)|.
Здесь используется ограниченность функции f, | f | £ M. Отметим, что при доказательстве использовалось то, что функция определена на некотором объемлющем множестве R. Так, например, для интеграла 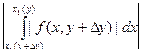 функция f должна быть определена на отрезке [ A, B ], лежащем вне области D (см. рисунок)
функция f должна быть определена на отрезке [ A, B ], лежащем вне области D (см. рисунок)
Определение. Пусть функция f (x, y) определена на [ a, b ] для любого y Î Y. Говорят, что f (x, y) равномерно сходится к g (x) на [ a, b ] при y ® y 0 если
" e >0 $ d >0 " x Î [a,b] " y Î U d (y0): |f(x,y) - g(x)|< e.
Это понятие является обобщением понятия равномерной сходимости функциональной последовательности f (x, y) 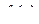 равномерно сходится на [ a, b ] к g (x) при n ® ¥, где вместо дискретного переменного n (индекса) выступает «непрерывный» параметр y.
равномерно сходится на [ a, b ] к g (x) при n ® ¥, где вместо дискретного переменного n (индекса) выступает «непрерывный» параметр y.
Теорема. (Аналог теоремы о непрерывности предельной функции, равномерно сходящейся последовательности непрерывных функций). Если f (x, y) непрерывна и равномерно сходится к g (x) на [ a, b ] при y ® y 0 , то функция g (x) непрерывна на [ a, b ].
Доказательство. Выпишем неравенства
| g (x)- g (x 0)|=| g (x)- f (x, y) + f (x, y)- f (x 0, y)- g (x 0)+ f (x 0, y)| £ | g (x)- f (x, y)|+ | f (x, y)- f (x 0, y)|+ | g (x 0)- f (x 0, y)|. Для заданного e сначала выбираем d окрестность точки x 0 так, чтобы в этой окрестности | f (x, y)- f (x 0, y)|< e для любых y из некоторой окрестности точки y 0. Это можно сделать в силу равномерной непрерывности функции f (x, y). Величины | g (x)- f (x, y)|, | g (x 0)- f (x 0, y)| можно сделать также < e выбором ещё меньшей окрестности точки y 0 для всех x в силу равномерной сходимости f (x, y) к g (x).
Теорема. (Аналог теоремы о переходе к пределу под знаком интеграла или, что тоже, о почленном интегрировании равномерно сходящейся последовательности непрерывных функций). Если f (x, y) непрерывна и равномерно сходится к g (x) на [ a, b ] при y ® y 0, то
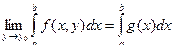 .
.
Доказательство. 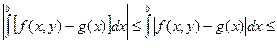 | b - a | e.
| b - a | e.
2. Интегрирование интегралов зависящих от параметра
Предположим, что область является областью типа А и В. Из формул выражения двойного интеграла через повторные следуют следующие формулы
3. Дифференцирование интегралов, зависящих от параметра
Теорема (Лейбниц). Если f и  непрерывны в [ a, b ] ´ [ c, d ], то F (y) =
непрерывны в [ a, b ] ´ [ c, d ], то F (y) = 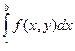
дифференцируема на [ c, d ] и 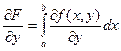 .
.
Доказательство.
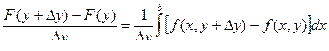 =
=  =
=  , 0< q <1. Тогда
, 0< q <1. Тогда
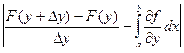 £
£ 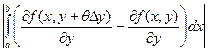 .
.
Из этого неравенства и равномерной непрерывности функции  следует требуемое утверждение.
следует требуемое утверждение.
Рассмотрим область типа В, указанную на рисунке и функцию f, определенную на прямоугольнике R, содержащем область D.
Теорема. Если f и ее производная  непрерывны на R, x 1 (y), x 2 (y) имеют непрерывные на [ c, d ] производные, то F (y) =
непрерывны на R, x 1 (y), x 2 (y) имеют непрерывные на [ c, d ] производные, то F (y) = 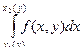 также имеет производную
также имеет производную
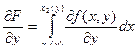 +
+ 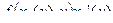 -
-  .
.
Доказательство. Рассмотрим функцию Ф(u, v, y) = 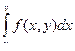 , определенную на прямоугольном параллелепипеде
, определенную на прямоугольном параллелепипеде 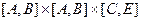 , Для нее существуют непрерывные частные производные
, Для нее существуют непрерывные частные производные 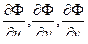 . Непрерывность функции
. Непрерывность функции  =
= 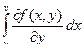 следует из равномерной непрерывности функции
следует из равномерной непрерывности функции 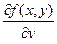 . Дифференцируя сложную функцию F (y) =
. Дифференцируя сложную функцию F (y) = 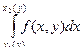 = Ф(y, x 1 (y), x 2 (y)) получим требуемое равенство.
= Ф(y, x 1 (y), x 2 (y)) получим требуемое равенство.
§2. Несобственные интегралы, зависящие от параметра
1. Равномерная сходимость несобственного интеграла от параметра
Рассмотрим интеграл
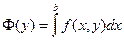 (1)
(1)
 , y Î Y.
, y Î Y.
Предположим, что при некоторых y интеграл (1) является несобственным. Так, если  и при некотором y интеграл (1) имеет единственную особенность в b, то условием сходимости интеграла (1) будет существование конечного предела
и при некотором y интеграл (1) имеет единственную особенность в b, то условием сходимости интеграла (1) будет существование конечного предела
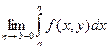 .
.
Если при заданном y интеграл сходится, то для любого h Î [ a, b) интеграл 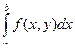 (называемый остатком) будет существовать и условие сходимости можно записать в виде
(называемый остатком) будет существовать и условие сходимости можно записать в виде 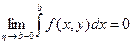 . В случае расходимости этого интеграла, естественно считать, что условие
. В случае расходимости этого интеграла, естественно считать, что условие 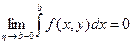 не выполнено. Таким образом, условие сходимости будет в дальнейшем записываться в виде
не выполнено. Таким образом, условие сходимости будет в дальнейшем записываться в виде
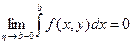 .
.
Определение. Пусть интеграл с параметром  для всех или для некоторых y Î Y имеет единственную особенность в b (если b конечное, интеграл 2-го рода) или в + ¥ (интеграл 2-го рода). Сходящийся на Y интеграл называется равномерно сходящимся на Y, если
для всех или для некоторых y Î Y имеет единственную особенность в b (если b конечное, интеграл 2-го рода) или в + ¥ (интеграл 2-го рода). Сходящийся на Y интеграл называется равномерно сходящимся на Y, если
" e >0 $ d >0 " h Î (b - d, b) " y Î Y:  (для интеграла 2-го рода)
(для интеграла 2-го рода)
" e >0 $ M " h Î (M,+ µ) " y Î Y: 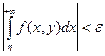 (для интеграла 1-го рода)
(для интеграла 1-го рода)
Признак Вейерштрасса равномерной сходимости
Если существует функция g (x), определенная на [ a, b) (b – конечное или + ¥), интегрируемая на любом [ a, h), h Î (a, b) такая, что
1) |f(x,y)| £ g(x), a £ x < b, " y Î Y
2)  сходится,
сходится,
то интеграл  сходится равномерно на Y.
сходится равномерно на Y.
Утверждение следует из неравенств  .
.
Теорема. (Переход к пределу под знаком интеграла) Пусть  и f (x, y) определена и непрерывна на [ a, b) по x для всех y Î Y. Если для любых h Î (a, b) функция f (x, y) равномерно сходится к g (x) на [ a, b - h ] при y ® y 0, интеграл
и f (x, y) определена и непрерывна на [ a, b) по x для всех y Î Y. Если для любых h Î (a, b) функция f (x, y) равномерно сходится к g (x) на [ a, b - h ] при y ® y 0, интеграл  равномерно сходится на Y,
равномерно сходится на Y, 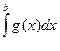 сходится. Тогда
сходится. Тогда
 .
.

Доказательство.
 =
= 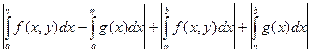 .
.
Для e >0 выбираем h так, что 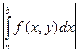
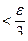 ,
, 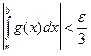 для всех y (равномерная сходимость
для всех y (равномерная сходимость 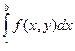 и сходимость
и сходимость 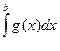 ). Для выбранного таким образом h можно найти окрестность точки y 0, в которой
). Для выбранного таким образом h можно найти окрестность точки y 0, в которой 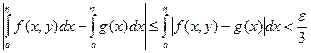 (равномерная сходимость f (x, y) к g (x) на [ a, b - h ]).
(равномерная сходимость f (x, y) к g (x) на [ a, b - h ]).
Критерий Коши равномерной сходимости (интеграла 2-го рода). Для равномерной сходимости интеграла 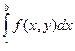 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы
" e >0 $ d >0 " y Î Y " h ¢, h ¢¢ Î (b- d,b): 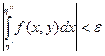 .
.
Достаточность. При выполнении условия 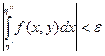 для " y Î Y " h ¢, h ¢¢ Î (b - d, b) можно перейти к пределу при h ¢¢ ® b. Тогда для " y Î Y " h ¢ Î (b - d, b):
для " y Î Y " h ¢, h ¢¢ Î (b - d, b) можно перейти к пределу при h ¢¢ ® b. Тогда для " y Î Y " h ¢ Î (b - d, b): 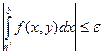 , что означает равномерную сходимость интеграла
, что означает равномерную сходимость интеграла 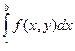 .
.
Необходимость. Имеем " e >0 $ d >0 " y Î Y " h Î (b - d, b):  . Тогда при h ¢, h ¢¢ Î (b - d, b) будет выполнено
. Тогда при h ¢, h ¢¢ Î (b - d, b) будет выполнено 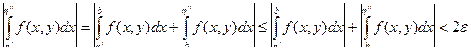 .
.
2. Непрерывность несобственного интеграла от параметра
Теорема 2. Если f (x, y) определена и непрерывна на [ a, b) ´ [ c, d ], интеграл F (y) = 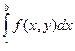 сходится равномерно на [ c, d ], то этот интеграл является непрерывной функцией.
сходится равномерно на [ c, d ], то этот интеграл является непрерывной функцией.
Доказательство.
| F (y + D y) - F (y)| = 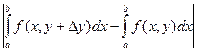 £
£ 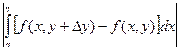 +
+ 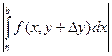 +
+ 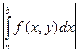 .
.
Второй и третий интегралы могут быть сделаны меньше заданного e выбором h в силу равномерной сходимости интеграла 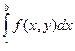 . После выбора h первый интеграл может быть сделан меньше заданного e выбором достаточно мелкого разбиения в силу равномерной непрерывности функции f (x, y) на прямоугольнике [ a, h ]
. После выбора h первый интеграл может быть сделан меньше заданного e выбором достаточно мелкого разбиения в силу равномерной непрерывности функции f (x, y) на прямоугольнике [ a, h ] 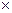 [ c, d ].
[ c, d ].
3. Интегрирование интегралов зависящих от параметра
Теорема. Если функция f (x, y) определена и непрерывна на [ a, b) ´ [ c, d ], интеграл F (y) = 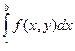 сходится равномерно на [ c, d ], существует интеграл
сходится равномерно на [ c, d ], существует интеграл 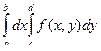 , то
, то
 =
= 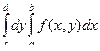 =
= 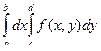 .
.
Доказательство. Для любого h Î [ a, b)
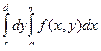 =
= 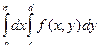 . Отсюда следует требуемое утверждение, если учесть, что
. Отсюда следует требуемое утверждение, если учесть, что  сходится равномерно на [ c, d ] к
сходится равномерно на [ c, d ] к 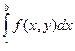 при h ® b. Действительно,
при h ® b. Действительно,  .
.
Эту теорему можно обобщить
Теорема. Если функция f (x, y) определена и непрерывна на [ a, b) ´ [ c, d), интеграл 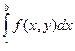 сходится равномерно на любом [ c, h ], интеграл
сходится равномерно на любом [ c, h ], интеграл  сходится равномерно на любом [ a, x ] и существует один из повторных интегралов
сходится равномерно на любом [ a, x ] и существует один из повторных интегралов
 ,
, 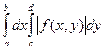 , то существует и другой и выполняется равенство
, то существует и другой и выполняется равенство
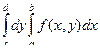 =
= 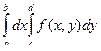 .
.
Без доказательства.
4. Дифференцирование интегралов, зависящих от параметра
Лемма. Если функция f (x, y) непрерывна на [ a, b) ´ [ c, d ], то сходимость интеграла 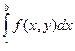 эквивалентна условию: для любой последовательности h k ® b, h 0 = a, h k Î [ a, b) сходится ряд
эквивалентна условию: для любой последовательности h k ® b, h 0 = a, h k Î [ a, b) сходится ряд  . Аналогично для равномерной сходимости: для равномерная сходимость интеграла
. Аналогично для равномерной сходимости: для равномерная сходимость интеграла 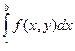 на множестве Y эквивалентна условию: для любой последовательности h k ® b, h 0 = a, h k Î [ a, b) равномерно на Y сходится функциональный ряд
на множестве Y эквивалентна условию: для любой последовательности h k ® b, h 0 = a, h k Î [ a, b) равномерно на Y сходится функциональный ряд  .
.
Это утверждение следует из определения предела 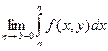 по Гейне и выражения для частичных сумм ряда
по Гейне и выражения для частичных сумм ряда 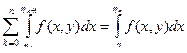 .
.
Теорема. Пусть функции f (x, y) и  непрерывны на [ a, b) ´ [ c, d ]. Если
непрерывны на [ a, b) ´ [ c, d ]. Если 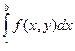 сходится для всех y а
сходится для всех y а  сходится равномерно на [ c, d ], то функция F (y) =
сходится равномерно на [ c, d ], то функция F (y) = 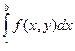 дифференцируема на этом отрезке и
дифференцируема на этом отрезке и
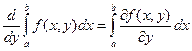 .
.
Доказательство. Пусть h n ® b, h n Î [ a, b), h 0 = a. Согласно лемме
F (y) = 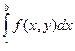 =
= 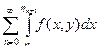 . Таким образом, функциональный ряд
. Таким образом, функциональный ряд 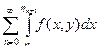 сходится для всех y. Далее,
сходится для всех y. Далее,  . Таким образом, ряд из производных сходится равномерно на [ c, d ]. По теореме о почленном дифференцировании функционального ряда
. Таким образом, ряд из производных сходится равномерно на [ c, d ]. По теореме о почленном дифференцировании функционального ряда 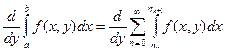 =
=  .
.
Пример. Гамма функция Эйлера Г(p) = 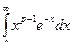 , p > 0.
, p > 0.
Г(p) непрерывна на (0, µ). Г(p) = 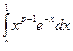 +
+ 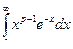 .
.
Докажем непрерывность функций 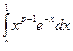 ,
, 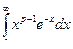 на (0, µ).
на (0, µ).
1) 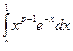 £
£  , p Î [ e, A ].
, p Î [ e, A ].  сходится и по признаку Вейерштрасса интеграл
сходится и по признаку Вейерштрасса интеграл 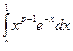 сходится равномерно на [ e, A ] и, следовательно, является непрерывной функцией на этом множестве [ e, A ].
сходится равномерно на [ e, A ] и, следовательно, является непрерывной функцией на этом множестве [ e, A ].
2) 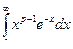 £
£  , p Î [ e, A ].
, p Î [ e, A ].  сходится и по признаку Вейерштрасса интеграл
сходится и по признаку Вейерштрасса интеграл 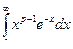 сходится равномерно на [ e, A ] и, следовательно, является непрерывной функцией на множестве [ e, A ].
сходится равномерно на [ e, A ] и, следовательно, является непрерывной функцией на множестве [ e, A ].
Для гамма функции Эйлера справедлива формула
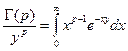 (1)
(1)
Это равенгство получается после замены x ® xy.
G (p) = 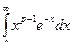 =
= 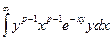 =
= 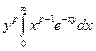 .
.
2. Бэта функция Эйлера В(p, q) = 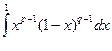 , p > 0, q >0.
, p > 0, q >0.
Сделаем замену 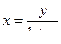 , dx =
, dx =  .
.
В(p, q) =  =
= 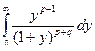 .
.
В(p, q) =  (2)
(2)
3. Другие свойства функций Эйлера
Из формулы (1) следует, что
 ,
,  . Интегрируя, получим
. Интегрируя, получим 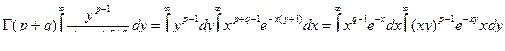 . Откуда, используя (2)
. Откуда, используя (2)
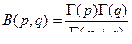 .
.
В(p,1- p) = Г 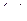 Г
Г  =
= 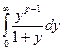 =
= 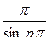 ,0< p <1.
,0< p <1.
Г(1) = 1, Г(p +1) = p Г(p).
Отметим, что из этой формулы следует, что Гамма функцию достаточно знать на интервале (0, 1/2).
Интеграл 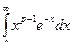 сходится для p >0 и
сходится для p >0 и 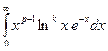 сходится равномерно на любом отрезке [ e, A ], для 0 < e < A. Поэтому интеграл можно дифференцировать по параметру. Докажем равномерную сходимость интегралов
сходится равномерно на любом отрезке [ e, A ], для 0 < e < A. Поэтому интеграл можно дифференцировать по параметру. Докажем равномерную сходимость интегралов 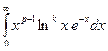 .
.
В окрестности нуля | ln x | £ 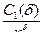 для d > 0 существует C 1 (d).
для d > 0 существует C 1 (d).
В окрестности бесконечности | ln x | £ 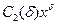 для d > 0 существует C 2 (d).
для d > 0 существует C 2 (d).
Равномерная сходимость интеграла Г( k ) (p)= 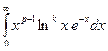 на любом отрезке [ e, A ] следует из оценок
на любом отрезке [ e, A ] следует из оценок 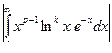 £
£  +
+ 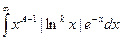 £
£  +
+ 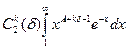 , для всех p Î [ e, A ]. Здесь для e >0 следует выбрать d так, чтобы e - k d оставалось больше нуля.
, для всех p Î [ e, A ]. Здесь для e >0 следует выбрать d так, чтобы e - k d оставалось больше нуля.
4. Примеры вычисления несобственных интегралов, зависящих от параметра
Формула Фруллани. Функция f (x) непрерывна и интеграл 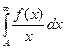 существует для любого A > 0.
существует для любого A > 0.
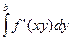 =
= 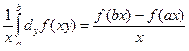 ,
, 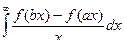 =
= 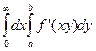 =
= 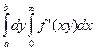 =
= 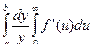 =
=  =- f (0)
=- f (0)  .
.
 = f(0)
= f(0)  , (a>0,b>0).
, (a>0,b>0).
Интегрированием по частям вычисляются интегралы
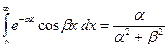 , a ³ 0,
, a ³ 0, 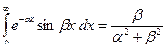 , a ³ 0.
, a ³ 0.
Другой способ: Положим g = - a + i b, 
 , откуда и следуют указанные формулы.
, откуда и следуют указанные формулы.
Вычислить
 .
.
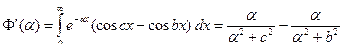 ,
, 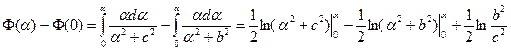 =
= 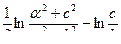 ,
, 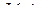
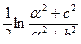
Интеграл Пуассона
I = 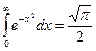 .
.
I 2 = 
 =
= 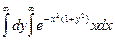 =
= 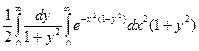 =
= 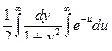 =
= 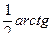
 =
= 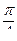 .
.
Интеграл I = 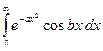 .
.
Интегрирование по частям I = 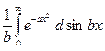 =
= 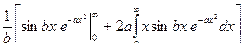 =
= 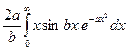 .
.
 =
=  I,
I, 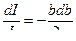 , I = C
, I = C 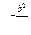 , I(0) =
, I(0) = 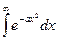 =
=  =
= 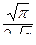 , I =
, I = 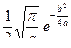 .
.
Вычислить интеграл F (a, b) = 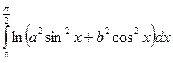 , a >0, b >0 (1)
, a >0, b >0 (1)
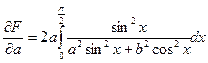 (2),
(2), 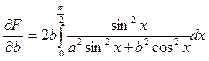
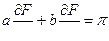 из (2) F (a, b) =
из (2) F (a, b) = 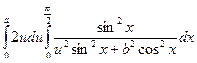 +С(b).
+С(b).
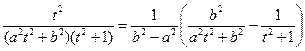
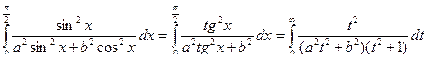 =
=  =
= 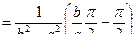 =
= 
F(a,b) = 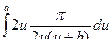 +C(b)=
+C(b)= 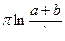 +C(b).
+C(b).
p ln b = F(b,b)= p ln 2 + C(b), C(b) = p 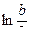 .
.
Глава 6. Преобразования базисов и координат, криволинейные координаты
§1. Преобразования базисов и координат
1.Отображение областей. Криволинейные координаты
Рассмотрим область V в системе координат (x, y, z) и область D в системе координат (x 1, x 2, x 3).

Кроме того, пусть задано взаимно-однозначное соответствие между этими областями, осуществляемое регулярным отображением (регулярное – взаимно-однозначное и такое, что прямое и обратное непрерывно дифференцируемы)
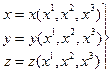 (1)
(1)
Будем предполагать, что матрица Якоби отображения (1) не вырождена всюду в области D. Наборы координат (x, y, z) и (x 1, x 2, x 3) можно интерпретировать следующим образом: каждая точка M из области V определяется, как ее исходными координатами (в дальнейшем это будут декартовы координаты), так и координатами (x 1, x 2, x 3), которые в отличии от исходных координат называются криволинейными координатами. В основе этой терминологии лежит геометрический подход. Так, если в (1) фиксировать две из трех координат x 1, x 2, x 3, то получим линию, которая называется координатной линией. Множество всевозможных линий, полученных фиксированием второй и третьей координат обозначим S 1 (параметром линии служит первая координата x 1). Аналогично определяются еще два семейства линий S 2, S 3. При сделанных предположениях через каждую точку будет проходить ровно по одной линии из этих семейств. Таким образом, задание точки однозначно определяется заданием трех линий l 1 Î S 1, l 2 Î S 2, l 3 Î S 3. Наряду с координатными линиями можно рассматривать координатные поверхности, которые получаются, если в (1) фиксировать одну из координат, а остальные две рассматривать, как параметры.
Рассмотрим три координатные линии, проходящие через заданную точку области V
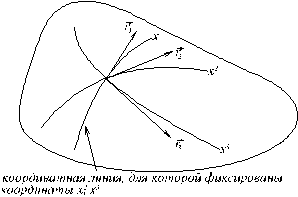
Касательные вектора в точке пересечения этих линий обозначим через
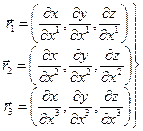 (2)
(2)
Эти вектора образуют базис, так как они не компланарны
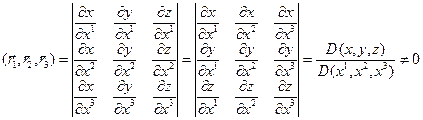 .
.
Для данного базиса единственным образом можно определить базис  1,
1,  2,
2,  3 такой, что (
3 такой, что (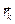 ,
,  j)=
j)=  . Подробнее об этом речь пойдет в одном из следующих пунктах. Такой базис называется взаимным. Векторы взаимного базиса определяются по формулам
. Подробнее об этом речь пойдет в одном из следующих пунктах. Такой базис называется взаимным. Векторы взаимного базиса определяются по формулам
 1=
1= 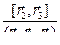 ,
,  2=
2= 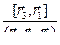 ,
,  3=
3= 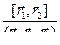 . (3)
. (3)
Определение. Криволинейная система координат (1) называется ортогональной, если в каждой точке области V базис (2) является ортогональным.
В случае ортогональной системы координат формулы (3) упрощаются. Будем предполагать, что тройка  правая. Положим H 1 =
правая. Положим H 1 =  , H 2 =
, H 2 =  , H 3 =
, H 3 = 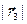 , величины H 1, H 2, H 3 называются коэффициентами Ламэ. В силу ортогональности (тройка правая)
, величины H 1, H 2, H 3 называются коэффициентами Ламэ. В силу ортогональности (тройка правая)
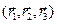 = H1 H2 H3,
= H1 H2 H3,  = H2 H3
= H2 H3 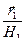 ,
,  = H3 H1
= H3 H1 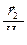 ,
,  = H1 H2
= H1 H2  .
.
Откуда следует, что
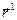 =
= 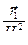 ,
,  =
= 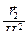 ,
, 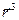 =
= 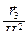 .
.
2. Наиболее употребительные случаи криволинейных координат в пространстве
Цилиндрические координаты
| 
| 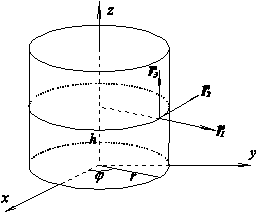
|
| x1=r
| x2= j
| x3=h
|
 1 =(cos j, sin j, 0) 1 =(cos j, sin j, 0)
|  2 =r (- sin j, cos j, 0) 2 =r (- sin j, cos j, 0)
|  3 =(0, 0, 1) 3 =(0, 0, 1)
|
| H1=1
| H2=r
| H3=1
|
| | | | |
Система цилиндрических координат ортогональна и 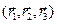 =
=  = r,
= r,
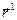 =
=  ,
,  =
= 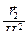 =
= 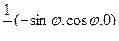 ,
, 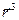 =
=  .
.
Сферические координаты
| 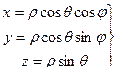
| 
|
| x1= r
| x2= j
| x3= q, q Î [- p /2, p /2]
|
 1 = (cos q cos j, cos q sin j, sin q) 1 = (cos q cos j, cos q sin j, sin q)
|  2 = 2 =
r cos q (-sin j,cos j,0)
|  3 =
r (-sin q cos j, - sin q sin j, cos q) 3 =
r (-sin q cos j, - sin q sin j, cos q)
|
| H1=1
| H2= r sin q,
| H3= r.
|
| | | | |
Система сферических координат ортогональна и 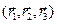 =
=  = r 2 cos q,
= r 2 cos q,
3. Взаимные, сопряженные базисы
В дальнейшем речь пойдет о базисах в трехмерном пространстве.
Определение. Базисы r i, r k называются взаимными или сопряженными, если выполнено условие
( r i, r k) = 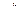 .
.
Теорема. Для любого базиса r i существует единственный взаимный базис.
Из условия r 1 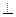 r 2, r 1
r 2, r 1 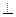 r 3, поэтому этот вектор надо искать в виде c [ r 2 , r 3 ], из условия ( r 1, r 1) = 1 находится множитель c. Таким образом,
r 3, поэтому этот вектор надо искать в виде c [ r 2 , r 3 ], из условия ( r 1, r 1) = 1 находится множитель c. Таким образом,
r 1 = [ r 2 , r 3 ]/( r 1, r 2, r 3), r 2 = [ r 3 , r 1 ]/( r 1, r 2, r 3), r 3 = [ r 1 , r 2 ]/( r 1, r 2, r 3).
Любой вектор пространства можно разложить по базисам
x = 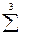 xk r k =
xk r k = 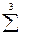 r k xk.
r k xk.
Координаты xk называются ковариантными координатами, а xk – контравариантными координатами.
Соглашение 1. В любом выражении, состоящем из некоторого числа сомножителей, наличие индекса у двух сомножителей на разных уровнях будет означать суммирование по этому индексу от 1 до 3. Следует придерживать единого порядка написания индексов суммирования. Договоримся при написании этих индексов следовать правилу: «левый внизу, правый вверху».
Соглашение 2. Иногда, если не возникает путаницы, стрелка над вектором будет опускаться. То же самое касается жирности шрифта для обозначения вектора ( r = r, если не возникает путаницы).
Например, формулы разложений по базисам будут выглядеть следующим образом
x = xk rk = rk xk.
Еще один пример: ai  cj =
cj = 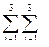 ai
ai  cj.
cj.
Найдем выражение для ко и контравариантных координат
x = xi ri = ri xi Þ
xi = (x, ri), xi = (x, ri) (1).
Подставляя выражения для координат в разложения вектора, получим формулы Гиббса
x = (x, ri) ri = ri (x, ri) (2)
Подставим выражения x из формул Гиббса (2) в (1)
xi = (x, rj)(rj, ri) = xj gji (3)
xi = (rj, ri) (x, rj) = gji xj (4)
Матрицы gji = (rj, ri), gji = (rj, ri) симметричны и называются метрическими тензорами. Беря в качестве x в формуле (2) вектора rj, rj получим формулы, связывающие векторы взаимных базисов с помощью метрических тензоров
rj = gji ri
rj = ri gji.
Подобные операции носят название операций поднимания и опускания индекса с помощью метрического тензора. Умножим первое равенство на rk второе на rk, получим
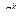 = gji gik
= gji gik
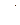 = gik gji.
= gik gji.
Эти равенства показывают, что матрицы метрических тензоров взаимно обратные.
4. Преобразование координат
Даны базисы ei, 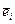 и ei,
и ei, 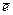 i. Обозначим матрицы, связывающие эти базисы
i. Обозначим матрицы, связывающие эти базисы 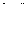 ,
, 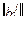 ,
, 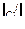 ,
,  .
.
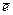 i = ej
i = ej  , ei =
, ei = 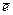 j
j  Þ
Þ 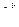
 =
= 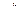 (5)
(5)
Равенство 
 =
= 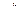 в развернутом виде выглядит следующим образом
в развернутом виде выглядит следующим образом
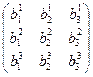
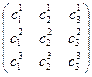 =
= 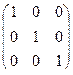 ,
,
Таким образом, если придерживаться правила порядка написания индексов суммирования: «левый внизу, правый вверху», то для матриц верхний индекс указывает номер строки, а нижний – номер столбца.
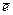 j =
j =  ei, ej =
ei, ej = 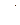
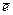 i Þ
i Þ 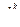
 =
= 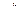 (6)
(6)
Последнее равенство в матричном виде:
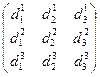
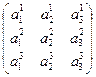 =
= 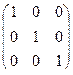 .
.
Умножая первое равенство из (5) на ek , а второе равенство из (6) на 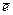 k получим выражения для матриц перехода между базисами
k получим выражения для матриц перехода между базисами
(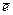 i, ek) = (ej
i, ek) = (ej  , ek)=
, ek)=  =
=  ,
,
(ek, 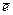 i)= (
i)= (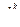
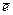 j,
j, 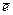 i)=
i)= 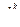
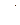 =
= 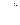 .
.
Таким образом,  =
=  . Аналогично показывается, что
. Аналогично показывается, что 
|
|
|


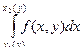

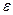 , используя равномерную непрерывность функции f можно подобрать D y так, что
, используя равномерную непрерывность функции f можно подобрать D y так, что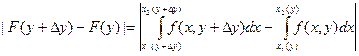 =
=  £
£ 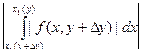 +
+ 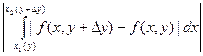 +
+ 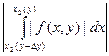 £ M|x1(y+ D y)-x1(y)|+(b - a) e + M| x2(y+ D y)-x2(y)|.
£ M|x1(y+ D y)-x1(y)|+(b - a) e + M| x2(y+ D y)-x2(y)|.
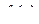 равномерно сходится на [ a, b ] к g (x) при n ® ¥, где вместо дискретного переменного n (индекса) выступает «непрерывный» параметр y.
равномерно сходится на [ a, b ] к g (x) при n ® ¥, где вместо дискретного переменного n (индекса) выступает «непрерывный» параметр y.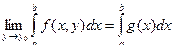 .
.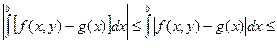 | b - a | e.
| b - a | e.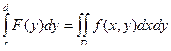 G(x)=
G(x)= 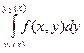
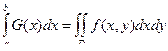
 непрерывны в [ a, b ] ´ [ c, d ], то F (y) =
непрерывны в [ a, b ] ´ [ c, d ], то F (y) = 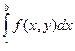
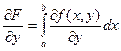 .
.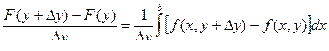 =
=  =
=  , 0< q <1. Тогда
, 0< q <1. Тогда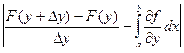 £
£ 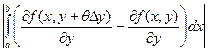 .
.
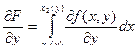 +
+ 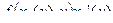 -
-  .
.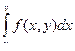 , определенную на прямоугольном параллелепипеде
, определенную на прямоугольном параллелепипеде 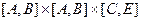 , Для нее существуют непрерывные частные производные
, Для нее существуют непрерывные частные производные 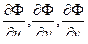 . Непрерывность функции
. Непрерывность функции  =
= 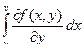 следует из равномерной непрерывности функции
следует из равномерной непрерывности функции 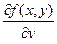 . Дифференцируя сложную функцию F (y) =
. Дифференцируя сложную функцию F (y) = 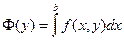 (1)
(1) , y Î Y.
, y Î Y.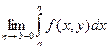 .
.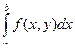 (называемый остатком) будет существовать и условие сходимости можно записать в виде
(называемый остатком) будет существовать и условие сходимости можно записать в виде 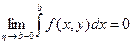 . В случае расходимости этого интеграла, естественно считать, что условие
. В случае расходимости этого интеграла, естественно считать, что условие  для всех или для некоторых y Î Y имеет единственную особенность в b (если b конечное, интеграл 2-го рода) или в + ¥ (интеграл 2-го рода). Сходящийся на Y интеграл называется равномерно сходящимся на Y, если
для всех или для некоторых y Î Y имеет единственную особенность в b (если b конечное, интеграл 2-го рода) или в + ¥ (интеграл 2-го рода). Сходящийся на Y интеграл называется равномерно сходящимся на Y, если (для интеграла 2-го рода)
(для интеграла 2-го рода)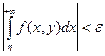 (для интеграла 1-го рода)
(для интеграла 1-го рода) сходится,
сходится, .
. равномерно сходится на Y,
равномерно сходится на Y, 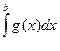 сходится. Тогда
сходится. Тогда .
.
 =
= 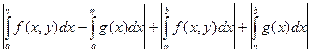 .
.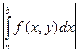
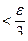 ,
, 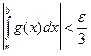 для всех y (равномерная сходимость
для всех y (равномерная сходимость 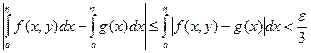 (равномерная сходимость f (x, y) к g (x) на [ a, b - h ]).
(равномерная сходимость f (x, y) к g (x) на [ a, b - h ]).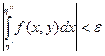 .
.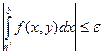 , что означает равномерную сходимость интеграла
, что означает равномерную сходимость интеграла 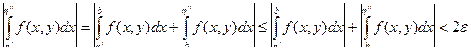 .
.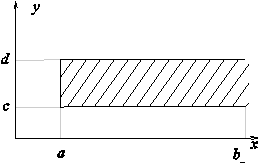
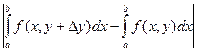 £
£ 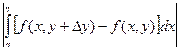 +
+ 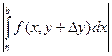 +
+ 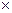 [ c, d ].
[ c, d ].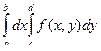 , то
, то =
= 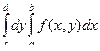 =
= 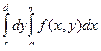 =
= 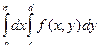 . Отсюда следует требуемое утверждение, если учесть, что
. Отсюда следует требуемое утверждение, если учесть, что  сходится равномерно на [ c, d ] к
сходится равномерно на [ c, d ] к  .
. сходится равномерно на любом [ a, x ] и существует один из повторных интегралов
сходится равномерно на любом [ a, x ] и существует один из повторных интегралов ,
, 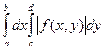 , то существует и другой и выполняется равенство
, то существует и другой и выполняется равенство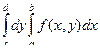 =
=  . Аналогично для равномерной сходимости: для равномерная сходимость интеграла
. Аналогично для равномерной сходимости: для равномерная сходимость интеграла 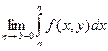 по Гейне и выражения для частичных сумм ряда
по Гейне и выражения для частичных сумм ряда 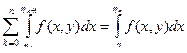 .
. сходится равномерно на [ c, d ], то функция F (y) =
сходится равномерно на [ c, d ], то функция F (y) = 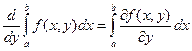 .
.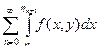 . Таким образом, функциональный ряд
. Таким образом, функциональный ряд  . Таким образом, ряд из производных сходится равномерно на [ c, d ]. По теореме о почленном дифференцировании функционального ряда
. Таким образом, ряд из производных сходится равномерно на [ c, d ]. По теореме о почленном дифференцировании функционального ряда 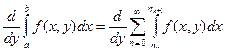 =
=  .
.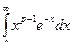 , p > 0.
, p > 0.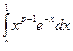 +
+ 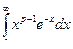 .
. , p Î [ e, A ].
, p Î [ e, A ].  , p Î [ e, A ].
, p Î [ e, A ]. 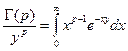 (1)
(1)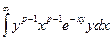 =
= 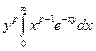 .
.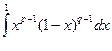 , p > 0, q >0.
, p > 0, q >0.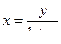 , dx =
, dx =  .
. =
= 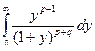 .
. (2)
(2) ,
,  . Интегрируя, получим
. Интегрируя, получим 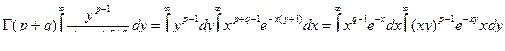 . Откуда, используя (2)
. Откуда, используя (2)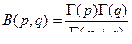 .
.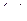 Г
Г  =
= 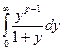 =
= 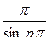 ,0< p <1.
,0< p <1.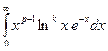 сходится равномерно на любом отрезке [ e, A ], для 0 < e < A. Поэтому интеграл можно дифференцировать по параметру. Докажем равномерную сходимость интегралов
сходится равномерно на любом отрезке [ e, A ], для 0 < e < A. Поэтому интеграл можно дифференцировать по параметру. Докажем равномерную сходимость интегралов 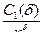 для d > 0 существует C 1 (d).
для d > 0 существует C 1 (d).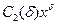 для d > 0 существует C 2 (d).
для d > 0 существует C 2 (d).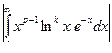 £
£  +
+ 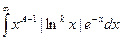 £
£  +
+ 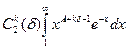 , для всех p Î [ e, A ]. Здесь для e >0 следует выбрать d так, чтобы e - k d оставалось больше нуля.
, для всех p Î [ e, A ]. Здесь для e >0 следует выбрать d так, чтобы e - k d оставалось больше нуля.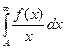 существует для любого A > 0.
существует для любого A > 0.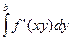 =
= 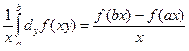 ,
, 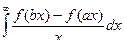 =
= 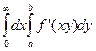 =
= 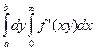 =
= 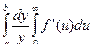 =
=  =- f (0)
=- f (0)  .
. = f(0)
= f(0) 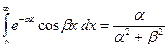 , a ³ 0,
, a ³ 0, 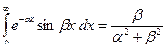 , a ³ 0.
, a ³ 0.
 , откуда и следуют указанные формулы.
, откуда и следуют указанные формулы. .
.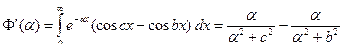 ,
, 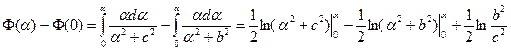 =
= 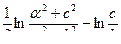 ,
, 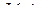
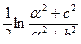
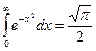 .
.
 =
= 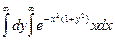 =
= 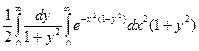 =
= 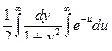 =
= 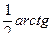
 =
= 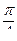 .
.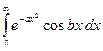 .
.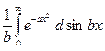 =
= 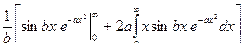 =
= 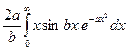 .
. =
=  I,
I, 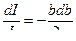 , I = C
, I = C 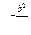 , I(0) =
, I(0) = 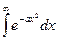 =
=  =
= 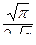 , I =
, I = 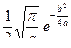 .
.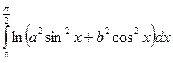 , a >0, b >0 (1)
, a >0, b >0 (1)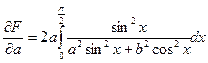 (2),
(2), 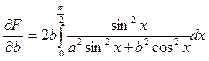
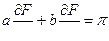 из (2) F (a, b) =
из (2) F (a, b) = 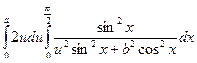 +С(b).
+С(b).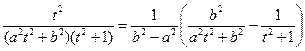
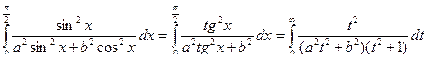 =
=  =
= 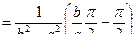 =
= 
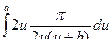 +C(b)=
+C(b)= 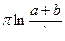 +C(b).
+C(b).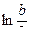 .
.
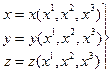 (1)
(1)
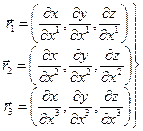 (2)
(2)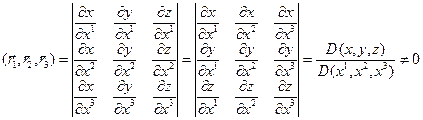 .
. 1,
1, 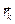 ,
,  . Подробнее об этом речь пойдет в одном из следующих пунктах. Такой базис называется взаимным. Векторы взаимного базиса определяются по формулам
. Подробнее об этом речь пойдет в одном из следующих пунктах. Такой базис называется взаимным. Векторы взаимного базиса определяются по формулам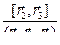 ,
, 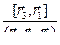 ,
, 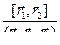 . (3)
. (3) правая. Положим H 1 =
правая. Положим H 1 =  , H 2 =
, H 2 =  , H 3 =
, H 3 = 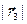 , величины H 1, H 2, H 3 называются коэффициентами Ламэ. В силу ортогональности (тройка правая)
, величины H 1, H 2, H 3 называются коэффициентами Ламэ. В силу ортогональности (тройка правая)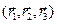 = H1 H2 H3,
= H1 H2 H3,  = H2 H3
= H2 H3 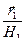 ,
,  = H3 H1
= H3 H1 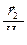 ,
,  = H1 H2
= H1 H2  .
.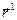 =
= 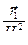 ,
,  =
= 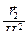 ,
, 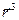 =
= 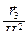 .
.

 = r,
= r, ,
, 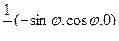 ,
,  .
.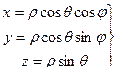

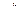 .
.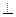 r 2, r 1
r 2, r 1 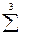 xk r k =
xk r k =  cj =
cj = 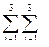 ai
ai 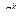 = gji gik
= gji gik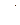 = gik gji.
= gik gji.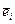 и ei,
и ei, 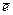 i. Обозначим матрицы, связывающие эти базисы
i. Обозначим матрицы, связывающие эти базисы 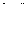 ,
, 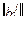 ,
, 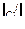 ,
,  .
. , ei =
, ei =  Þ
Þ 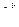

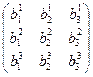
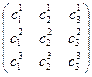 =
= 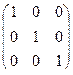 ,
,
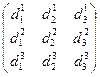
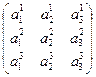 =
=  =
=  .
.