

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...
Топ:
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Интересное:
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Благодаря радиальной природе полярной системы координат, некоторые кривые могут быть достаточно просто описаны полярным уравнением, тогда как уравнение в прямоугольной системе координат было бы намного сложнее. Среди самых известных кривых: полярная роза, архимедова спираль, Лемниската, улитка Паскаля и кардиоида.
Окружность
Общее уравнение окружности с центром в (r0, 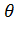 ) и радиусом a имеет вид:
) и радиусом a имеет вид:
r2-2rr0cos(φ - 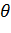 )+r02=a2.
)+r02=a2.
Это уравнение может быть упрощено для частных случаев, например
r(φ)=a
является уравнением, определяющим окружность с центром в полюсе и радиусом a.

Рисунок 3 - Окружность, заданная уравнением r(φ)=1
Прямая
Радиальные прямые (те, которые проходят через полюс) определяются уравнением
φ =θ,
где θ - угол, на который прямая отклоняется от полярной оси, то есть, θ = arctg,m где m - наклон прямой в прямоугольной системе координат. Нерадиальная прямая, перпендикулярно пересекает радиальную прямую φ =θ в точке (r0,θ) определяется уравнением
r(φ)=r0sec(φ-θ).
Полярная роза
Полярная роза - известная математическая кривая, похожая на цветок с лепестками. Она может быть определена простым уравнением в полярных координатах:
r(φ)=acos(kφ +θ0)
для произвольной постоянной θ0 (включая 0). Если k - целое число, то это уравнение будет определять розу с k лепестками для нечётных k, либо с 2k лепестками для чётных k. Если k - рациональное, но не целое, график, заданный уравнением, образует фигуру, подобную розе, но лепестки будут перекрываться. Если k - иррациональное, то роза состоит из бесконечного множества частично накладывающихся друг на друга лепестков. Розы с 2, 6, 10, 14 и т. д. лепестками этим уравнением определить невозможно. Переменная a определяет длину лепестков.
|
|
Если считать, что радиус не может быть отрицательным, то при любом натуральном k мы будем иметь k-лепестковую розу. Таким образом, уравнение r(φ)=cos(2φ) будет определять розу с двумя лепестками. С геометрической точки зрения радиус - это расстояние от полюса до точки и он не может быть отрицательным.

Рисунок 4 - Полярная роза задана уравнением r(φ)=2sin 4φ
Спираль Архимеда
Архимедова спираль названа в честь её изобретателя, древнегреческого математика Архимеда. Эту спираль можно определить с помощью простого полярного уравнения:
r(φ)=a+bφ.
Изменения параметра a приводят к повороту спирали, а параметра b - расстояния между витками, которое является константой для конкретной спирали. Спираль Архимеда имеет две ветви, одну для φ >0 а другую для φ <0. Две ветви плавно соединяются в полюсе. Зеркальное отображение одной ветви относительно прямой, проходящей через угол 90°/270°, даст другую ветвь. Эта кривая интересна тем, что была описана в математической литературе одной из первых, после конического сечения, и лучше других определяется именно полярным уравнением.

Рисунок 5 - Одна из ветвей спирали Архимеда, задаваемая уравнением r(φ)=φ для 0<θ <6π
Конические сечения
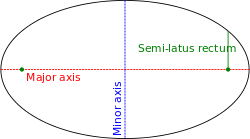
Рисунок 6 - Эллипс
Коническое сечение, один из фокусов которого находится в полюсе, а другой где-то на полярной оси (так, что малая полуось лежит вдоль полярной оси) задаётся уравнением:

где e - эксцентриситет, а l - фокальный параметр. Если e>1, это уравнение определяет гиперболу; если e=1, то параболу; если e<1, то эллипс. Отдельным случаем является e=0, определяющее окружность с радиусом l.
Комплексные числа
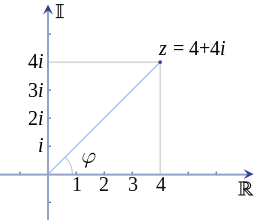
Рисунок 7 - Пример комплексного числа z, нанесённого на комплексную плоскость
Каждое комплексное число может быть представлено точкой на комплексной плоскости, и, соответственно, эта точка может определяться в декартовых координатах (прямоугольная или декартова форма), либо в полярных координатах (полярная форма). Комплексное число z может быть записано в прямоугольной форме так:
|
|
z=x+iy,
где i - мнимая единица, или в полярной:
z=rcdot (cos φ +isin φ)
и отсюда:
z=reiφ,
где e - число Эйлера. Благодаря формуле Эйлера, оба представления эквивалентны (6). (Следует отметить, что в этой формуле, подобно остальным формулам, содержащим возведения в степень углов, угол φ задан в радианах)
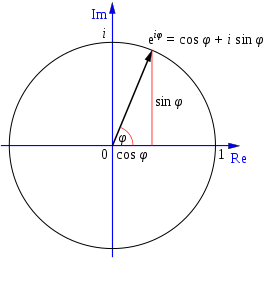
Рисунок 8 - Пример комплексного числа, нанесённого на график, с использованием формулы Эйлера
Для перехода между прямоугольным и полярным представлением комплексных чисел, могут использоваться указанные выше формулы преобразования между системами координат.
Операции умножения, деления и возведения в степень с комплексными числами, как правило, проще проводить в полярной форме. Согласно правилам возведения в степень:
· Умножение:
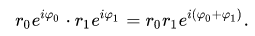
· Деление:

· Возведение в степень (формула Муавра):
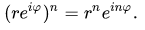
В математическом анализе
Операции математического анализа тоже можно сформулировать, используя полярные координаты.
Дифференциальное исчисление
Справедливы следующие формулы:
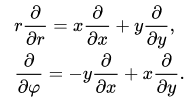
Чтобы найти тангенс угла наклона касательной к любой данной точке полярной кривой r(φ) в декартовых координатах, выразим их через систему уравнений в параметрическом виде:
x=r(φ)cosφ,
y=r(φ)sinφ.
Дифференцируя оба уравнения по φ получим:
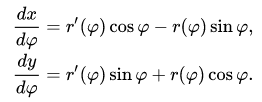
Разделив эти уравнения (второе на первое), получим искомый тангенс угла наклона касательной в декартовой системе координат в точке (r, r(φ)):
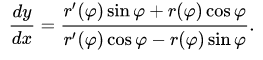
Интегральное исчисление

Рисунок 9 - Область R, которая образована полярной кривой r(φ) и лучами φ =a и φ =b
Пусть R - область, которую образуют полярная кривая r(φ) и лучи φ =a и φ =b, где 0<b-a<2π. Тогда площадь этой области находится определённым интегралом:
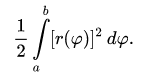

Рисунок 10 - Область R образована из n секторов (тут n=5)
Такой результат можно получить следующим образом. Сначала разобьём интервал [a,b] на произвольное число подынтервалов n. Таким образом, длина такого подынтервала ∆φ равна b-a (полная длина интервала), разделённая на n (число подынтервалов). Пусть для каждого подынтервала i=1, 2, …, nφi - средняя точка. Построим секторы с центром в полюсе, радиусами r(φi), центральными углами ∆φ и длиной дуги r(φi)∆ φ. Поэтому площадь каждого такого сектора будет
|
|

Отсюда, полная площадь всех секторов:
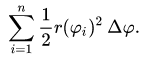
Если число подынтервалов n увеличивать, то погрешность такого приближенного выражения будет уменьшаться. Положив n 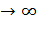 , полученная сумма станет интегральной. Предел этой суммы при ∆φ
, полученная сумма станет интегральной. Предел этой суммы при ∆φ 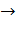 0 определяет вышеописанный интеграл:
0 определяет вышеописанный интеграл:

Векторный анализ
Для полярных координат можно применить элементы векторного анализа. Любое векторное поле F можно записать в полярной системе координат, используя единичные векторы:
er=(cosφ, sinφ)
в направлении r, и
eφ =(-sinφ, cosφ);
F =Frer+Fφ eφ.
Связь между декартовыми компонентами поля Fx и Fy и его компонентами в полярной системе координат задаётся уравнениями:
Fx=Frcosφ -Fφ sinφ;
Fy=Frsinφ +Fφ cosφ.
Соответствующим образом в полярной системе координат определяются операторы векторного анализа. Например, градиент скалярного поля Ф (r, φ) записывается:

Трёхмерное расширение
Полярная система координат распространяется в третье измерение двумя системами: цилиндрической и сферической, обе содержат двумерную полярную систему координат как подмножество. По сути, цилиндрическая система расширяет полярную добавлением ещё одной координаты расстояния, а сферическая - ещё одной угловой координаты.
Цилиндрические координаты
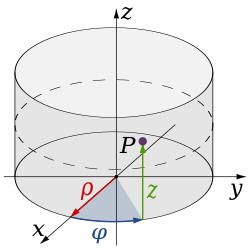
Рисунок 11 - Точка P начертана в цилиндрической системе координат
Цилиндрическая система координат, грубо говоря, расширяет плоскую полярную систему добавлением третьей линейной координаты, называемой «высотой» и равной высоте точки над нулевой плоскостью подобно тому, как Декартова система расширяется на случай трёх измерений. Третья координата обычно обозначается как z, образуя тройку координат (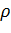 , φ, z).
, φ, z).
Тройку цилиндрических координат можно перевести в декартову систему следующими преобразованиями:

Сферические координаты

Рисунок 12 - Точка начертана в сферической системе координат
Также полярные координаты можно расширить на случай трёх измерений путём добавления угловой координаты θ, равным углу поворота от вертикальной оси z (называется зенитом или широтой, значения находятся в интервале от 0 до 180°). То есть, сферические координаты, это тройка (r, φ, θ), где r - расстояние от центра координат, φ - угол от оси x (как и в плоских полярных координатах), θ - широта. Сферическая система координат подобна географической системе координат для определения места на поверхности Земли, где начало координат совпадает с центром Земли, широта ∆ является дополнением θ и равна ∆ =90° -θ, а долгота l вычисляется по формуле l=φ -180°.
|
|
Тройку сферических координат можно перевести в декартову систему следующими преобразованиями:
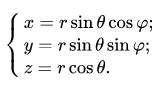
Обобщение на n измерений
Полярную систему координат можно расширить на случай n-мерного пространства. Пусть xi 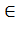 R, i=1, …, n - координатные векторы n-мерной прямоугольной системе координат. Необходимые координаты в n-мерный полярной системе можно вводить как угол отклонения вектора x
R, i=1, …, n - координатные векторы n-мерной прямоугольной системе координат. Необходимые координаты в n-мерный полярной системе можно вводить как угол отклонения вектора x 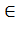 Rn от координатной оси xi+2.
Rn от координатной оси xi+2.
Для перевода обобщённых n-мерных полярных координат в декартовы можно воспользоваться следующими формулами:
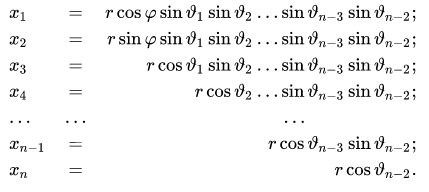
Как можно показать, случай n=2 соответствует обычной полярной системе координат на плоскости, а n=3 - обычной сферической системе координат.
Якобиан преобразования полярных координат в декартовы даётся формулой:

где n-мерный элемент объёма имеет вид:
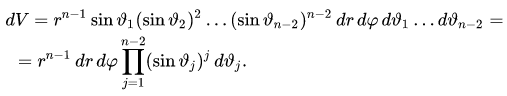
Применение
|
|
|

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!