440305
ПАМ
Толстиков А.В.
Практическое занятие 7. Многочлены над конечными полями
1. Функция Мебиуса и формула обращения Мебиуса.
2. Неприводимые многочлены над конечными полями и их число.
3. Порядок многочлена над конечным полем.
4. Критерий неприводимости многочлена и способы построения неприводимых многочленов над конечным полем.
5. Конструкция конечного поля из pn элементов.
6. Вычисления в конечных полях.
Литература. Нечаев В.И. – С. 42-48.
Глухов М.М. и др. -Т. 2. – С. 221-237.
Самсонов Б.Б., Плохов Е.М., Филоненков А.И. Компьютерная математика (основания информатики). Ростов-на-Дону: «Феникс», 2002. – С. 228-292.
.
Задачи для решения на практическом занятии и для самостоятельного решения
1. Составить таблицу значений функции Мебиуса для все целых чисел n из промежутка:
1) [1, 20]; 2) [21, 40]; 3) [41, 60].
2. Найти все нормированные неприводимые многочлены степени n над полем Z p для случаев.
1) p = 2, n = 4; 2) p = 2, n = 5; 3) p = 3, n = 2; 4) p = 3, n = 3.
3. Найти число нормированных неприводимый многочленов степени n над полем Fp для случаев.
1) p = 2, n = 8; 2) p = 2, n = 12; 3) p = 3, n = 10; 4) p = 5, n = 4.
4. Пусть m Î N, f – многочлен над полем Fp. Доказать, что f | (xm -1) тогда и только тогда, когда ord f | m.
5. Пусть f, g – взаимно простые многочлены над полем Fp. Доказать, что ord (fg)= НОД(ord (f), ord (g)).
6. Пусть n Î N, f – многочлен над полем Fp, g = f n, t – наименьшее неотрицательное число с условием p t ³ n. Доказать:
1) ord g = ord (f n) = p t × ord f;
2) если к тому же n > 0, то ord g < p deg g – 1.
7. Определить порядки многочленов над полем F 2:
1) x 2 + x + 1; 2) x 3 + x + 1; 3) x 5 + x + 1; 4) x 4 + x 3 + x 2 + x + 1.
8. Определить порядки многочленов над полем F 5:
1) x + 1; 2) x + 2; 3) x + 3; 4) x + 4; 5) x 2 + x + 1; 6) x 2 + x + 2; 4) x 2 + x + 3.
9. Найти число примитивных многочленов степени n над полем Fp для случаев.
1) p = 2, n = 8; 2) p = 2, n = 12; 3) p = 3, n = 10; 4) p = 5, n = 4.
10. Доказать, что данный многочлен f примитивный над полем F 2:
1) f = x 2 + x + 1; 2) x 3 + x + 1; 3) x 4 + x + 1; 4) x 5 + x 2 + 1; 5) x 6 + x + 1; 4) x 7 + x 3 + 1.
11. Определить порядки многочленов над полем F 2:
1) (x 2 + x + 1)5(x 3 + x + 1); 2) (x 2 + x + 1)7(x 3 + x + 1)3.
12. Приводим или нет многочлен x 5 -2 Î F 3[ x ] над полем F 3 и в случае его приводимости разложить его на множители.
13. Приводим или нет многочлен x 3 + x 2 + 1 Î F 3[ x ] над полем F 3 и в случае его приводимости разложить его на множители.
14. Приводим или нет многочлен x 4 + x 3 + x 3 + x 2 + 1 Î F 3[ x ] над полем F 3 и в случае его приводимости разложить его на множители.
15. Составить таблицы сложения и умножения элементов поля Fp (q), где q - корень многочлена f.
1) f = x 3 + x + 1, p = 2; 2) f = x + 2, p = 3.
16. Выполнить все арифметические действия над элементами a, b в поле Fp (q), где q - корень многочлена f.
1) f = x 4+ x +1, p = 2, a = (1101), b = (1010); 2) f = x 2+ 1, p = 3, a = (120), b=(012).
17. Представить элементы поля Fp (q), где q - корень многочлена f все возможными способами. Выполнить все арифметические операции над элементами a, b этого поля всевозможными способами и сравнить результаты.
1) f = x 4+ x +1, p = 2, a = (1001), b = (1010); 2) f = x 2+ 1, p = 3, a = (102), b=(212).
1. Составить программу, определяющую все неприводимые многочлены поля Fp степени n.
2. Составить программу для вычисления порядка данного многочлена.
3. Составить программу для нахождения примитивного многочлена над полем Fp степени n.
4. Составить программу для выполнения арифметических операций над элементами простого расширения Fp (q), где q - корень многочлена f = xn + a 1 xn - 1 +…+ an.
Степенное и целочисленное представления удобны для выполнения мультипликативных операций (умножения и деления).
Степенное представление ненулевых элементов.
Умножение: a i a j = a k , где k º i + j (mod q - 1).
Деление: a i / a j = a k , где k º i - j (mod q - 1).
Выписывается элемент 1.
2. Умножается полученный элемент на x.
Приведение многочлена, полученного на шаге 2 по модулю примитивного многочлена, порождающего данное поле.
Переход к пункту 2.
Пример 3. Генерировать все элементы поле 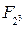 , f (x) = x 3 + x + 1 в полиномиальном представлении:
, f (x) = x 3 + x + 1 в полиномиальном представлении:
1, x, x 2 , x 3 = x + 1, x 4= x (x + 1) = x 2 + x, x 5= x (x 2 + x) = x 3 + x 2 = x 2 + x + 1,
x 6= x (x 2 + x + 1) = x 3 + x 2 + 1= x 2 + x.
При векторном и полиномиальном представлении элементов поля сложение и вычитание выполняются естественным образом как поразрядное сложение и соответственно вычитание по модулю p. При полиномиальном представлении элементов умножении элементов поля осуществляется по следующему алгоритму:
Обычное умножение полиномов.
2. Приведение по модулю p коэффициентов в полученном представлении.
440305
ПАМ
Толстиков А.В.
Практическое занятие 7. Многочлены над конечными полями
1. Функция Мебиуса и формула обращения Мебиуса.
2. Неприводимые многочлены над конечными полями и их число.
3. Порядок многочлена над конечным полем.
4. Критерий неприводимости многочлена и способы построения неприводимых многочленов над конечным полем.
5. Конструкция конечного поля из pn элементов.
6. Вычисления в конечных полях.
Литература. Нечаев В.И. – С. 42-48.
Глухов М.М. и др. -Т. 2. – С. 221-237.
Самсонов Б.Б., Плохов Е.М., Филоненков А.И. Компьютерная математика (основания информатики). Ростов-на-Дону: «Феникс», 2002. – С. 228-292.
.
Задачи для решения на практическом занятии и для самостоятельного решения
1. Составить таблицу значений функции Мебиуса для все целых чисел n из промежутка:
1) [1, 20]; 2) [21, 40]; 3) [41, 60].
2. Найти все нормированные неприводимые многочлены степени n над полем Z p для случаев.
1) p = 2, n = 4; 2) p = 2, n = 5; 3) p = 3, n = 2; 4) p = 3, n = 3.
3. Найти число нормированных неприводимый многочленов степени n над полем Fp для случаев.
1) p = 2, n = 8; 2) p = 2, n = 12; 3) p = 3, n = 10; 4) p = 5, n = 4.
4. Пусть m Î N, f – многочлен над полем Fp. Доказать, что f | (xm -1) тогда и только тогда, когда ord f | m.
5. Пусть f, g – взаимно простые многочлены над полем Fp. Доказать, что ord (fg)= НОД(ord (f), ord (g)).
6. Пусть n Î N, f – многочлен над полем Fp, g = f n, t – наименьшее неотрицательное число с условием p t ³ n. Доказать:
1) ord g = ord (f n) = p t × ord f;
2) если к тому же n > 0, то ord g < p deg g – 1.
7. Определить порядки многочленов над полем F 2:
1) x 2 + x + 1; 2) x 3 + x + 1; 3) x 5 + x + 1; 4) x 4 + x 3 + x 2 + x + 1.
8. Определить порядки многочленов над полем F 5:
1) x + 1; 2) x + 2; 3) x + 3; 4) x + 4; 5) x 2 + x + 1; 6) x 2 + x + 2; 4) x 2 + x + 3.
9. Найти число примитивных многочленов степени n над полем Fp для случаев.
1) p = 2, n = 8; 2) p = 2, n = 12; 3) p = 3, n = 10; 4) p = 5, n = 4.
10. Доказать, что данный многочлен f примитивный над полем F 2:
1) f = x 2 + x + 1; 2) x 3 + x + 1; 3) x 4 + x + 1; 4) x 5 + x 2 + 1; 5) x 6 + x + 1; 4) x 7 + x 3 + 1.
11. Определить порядки многочленов над полем F 2:
1) (x 2 + x + 1)5(x 3 + x + 1); 2) (x 2 + x + 1)7(x 3 + x + 1)3.
12. Приводим или нет многочлен x 5 -2 Î F 3[ x ] над полем F 3 и в случае его приводимости разложить его на множители.
13. Приводим или нет многочлен x 3 + x 2 + 1 Î F 3[ x ] над полем F 3 и в случае его приводимости разложить его на множители.
14. Приводим или нет многочлен x 4 + x 3 + x 3 + x 2 + 1 Î F 3[ x ] над полем F 3 и в случае его приводимости разложить его на множители.
15. Составить таблицы сложения и умножения элементов поля Fp (q), где q - корень многочлена f.
1) f = x 3 + x + 1, p = 2; 2) f = x + 2, p = 3.
16. Выполнить все арифметические действия над элементами a, b в поле Fp (q), где q - корень многочлена f.
1) f = x 4+ x +1, p = 2, a = (1101), b = (1010); 2) f = x 2+ 1, p = 3, a = (120), b=(012).
17. Представить элементы поля Fp (q), где q - корень многочлена f все возможными способами. Выполнить все арифметические операции над элементами a, b этого поля всевозможными способами и сравнить результаты.
1) f = x 4+ x +1, p = 2, a = (1001), b = (1010); 2) f = x 2+ 1, p = 3, a = (102), b=(212).
1. Составить программу, определяющую все неприводимые многочлены поля Fp степени n.
2. Составить программу для вычисления порядка данного многочлена.
3. Составить программу для нахождения примитивного многочлена над полем Fp степени n.
4. Составить программу для выполнения арифметических операций над элементами простого расширения Fp (q), где q - корень многочлена f = xn + a 1 xn - 1 +…+ an.
Функция Мебиуса и формула обращения Мебиуса
Определение 1. Функцией Мебиуса называется функция m: N ® {-1, 0, 1}, определенная равенством:
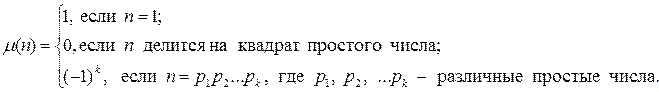
Теорема 2 (теорема обращения Мебиуса). Пусть f и g – функции натурального аргумента. Тогда равенство
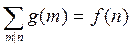 (3)
(3)
верно тогда и только тогда, когда
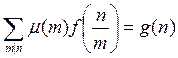 . (4)
. (4)



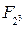 , f (x) = x 3 + x + 1 в полиномиальном представлении:
, f (x) = x 3 + x + 1 в полиномиальном представлении: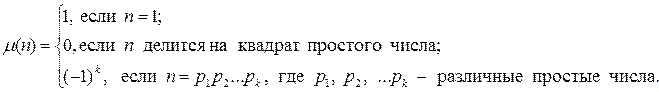
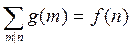 (3)
(3)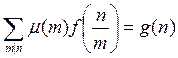 . (4)
. (4)


