Теорема 1. Многочлен f (x) Î F [ x ] степени n >0 неприводим над полем F = 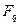 , q = pm, тогда и только тогда, когда выполняются условия:
, q = pm, тогда и только тогда, когда выполняются условия:
1) (f (x), f ¢ (x)) = 1;
2) уравнение
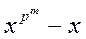 (1)
(1)
имеет в кольце R = F [ x ]/ f (x) ровно pm решений.
Доказательство. Необходимость. Пусть многочлен f (x) степени n >0 неприводим над полем F. Покажем, что уравнение (1) имеет в кольце R ровно pm решений. Уравнение (1) имеет в кольце R по крайней мере pm решений. Это элементы множества
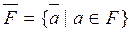 ,
,
где ` a – класс вычетов элемента a Î F по модулю f (x). Действительно,
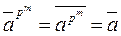 ,
,
при этом для любых элементов a 1, a 2, если a 1 ¹ a 2, то f (x) не делит a 1 - a 2 и ` a 1 ¹ ` a 2.
Так как многочлен f (x) неприводим над F, то он не имеет кратных множителей и многочлены f (x) и f ¢ (x) взаимно простые. Так как в этом случае кольцо R является полем и уравнение (1) не может иметь в кольце R более решений pm. Таким образом условия 1-2 выполняются.
Достаточность. Пусть выполняются условия 1-2. Тогда уравнение (1) не имеет других решений, кроме элементов поля F. Докажем, что многочлен f (x) неприводим над полем F. Допустим противное, что многочлен f (x) приводим над полем F. Тогда n >1 и существуют такие многочлены f 1(x), f 2(x) Î F [ x ] степени >0, что
f (x) = f 1(x) f 2(x).
Докажем теперь, что уравнение (1) имеет решение в R \ ` F, и тем самым приходим к противоречию, доказывающему неприводимость f (x). Так как выполняется условие 1, то многочлен f (x) не имеет кратных множителей и многочлены f 1(x) и f 2(x) взаимно простые. Тогда существуют такие многочлены u (x), v (x) Î F [ x ], что
u (x), f 1(x) + v (x) f 2(x) = 1. (2)
При этом можно считать, что deg u (x) < deg f 2(x). Так как в противном случае многочлен u (x) можно разделить на f 2(x) с остатком u (x) = f 2(x) g (x) + r (x), deg r (x)<deg f 2(x) и тогда получаем:
r (x), f 1(x) + (f 1(x) g (x)+ v (x)) f 2(x) = 1.
Далее в равенстве (2) u (x) ¹ 0. В кольце R имеет место равенство для классов
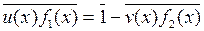 .
.
Тогда
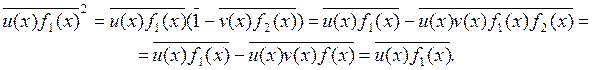
Следовательно,
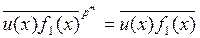
и 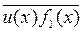 - решение уравнения (1) в кольце R. При этом
- решение уравнения (1) в кольце R. При этом 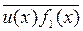 Ï ` F, так как
Ï ` F, так как
0 < deg u (x), f 1(x) < deg f (x).ÿ
Способ распознавания приводимости или неприводимости многочлена f (x) Î F [ x ] степени n >1 над полем F.
1) Если (f (x), f ¢ (x)) ¹ 1, то многочлен f (x) – приводим над полем F.
2) Если (f (x), f ¢ (x)) = 1, то подсчитываем число решений многочлен (1) в кольце R.
Произвольный элемент кольца R можно записать в виде
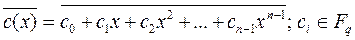 .
.
Элемент 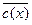 является решением уравнения (1) тогда и только тогда, когда выполняется равенство
является решением уравнения (1) тогда и только тогда, когда выполняется равенство
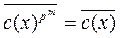 ,
,
которое можно записать в виде
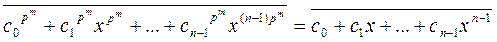 .
.
Так как 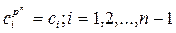 , то отсюда получаем
, то отсюда получаем
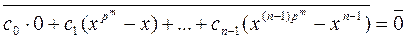 . (3)
. (3)
Для каждого i = 1,…, n -1 существует такой однозначно определенный многочлен
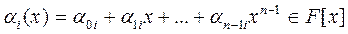 ,
,
что
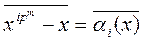 .
.
Тогда равенство (3) представляется в виде
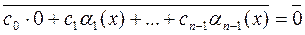 . (4)
. (4)
Так как deg f (x) = n, deg a i (x) < n при i = 1,…, n -1, то равенство (4) равносильно в кольце F [ x ] условию
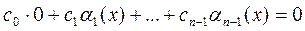 . (5)
. (5)
Приравнивая коэффициенты в правой и левой частях равенства (4), получим систему линейных уравнений:
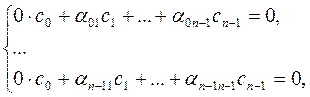
которую в матричной форме
AC=0, (6)
где
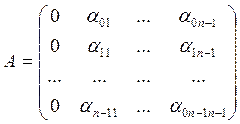 .
.
Таким образом число решений уравнения (1) в кольце R равно числу решений СЛУ (6), т.е. равно 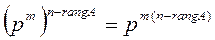 . По теореме 1 многочлен f (x) Î F [ x ] неприводим над полем F =
. По теореме 1 многочлен f (x) Î F [ x ] неприводим над полем F = 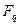 , q = pm, тогда и только тогда, когда n -rang A =1, т.е. rang A = n -1.
, q = pm, тогда и только тогда, когда n -rang A =1, т.е. rang A = n -1.
Используя изложенный выше алгоритм, можно разложить многочлен f (x) Î F [ x ] в случае приводимости в произведение многочленов меньшей степени. Рассмотрим два случая:
1) d (x) = НОД(f (x), f ¢ (x)) ¹ 1.
Если при этом f ¢ (x) ¹ 0, то 0 £ deg f ¢ (x) < n. Значит 0 < deg d (x) < n и f (x) = d (x) f 1(x), 0 < deg f 1(x) < n..
Если f ¢ (x) = 0, то из равенств
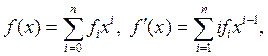
получаем, что ifi = 0 при i = 1,…, n. Следовательно, если j = 1,…, n и fj ¹ 0, то p | j, так как характеристика поля F равна p. Поэтому многочлен f (x) имеет вид
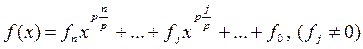
Это в виду равенства
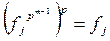
можно записать в виде
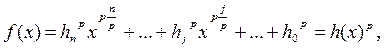
где
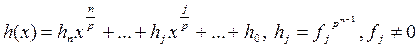 .
.
2) (f (x), f ¢ (x)) = 1. Если многочлен f (x) приводим над F, то rang A < n -1 и существует нулевое решение C = (с 0, с 1,…, с n -1), где с i ¹ 0, при некотором i = 1,…, n -1. Тогда 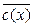 решение уравнения (1), где
решение уравнения (1), где 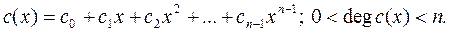
Теорема 2. Пусть q = pm. Если f (x) Î Fq [ x ] – нормированный многочлен степени > 0 и многочлен h (x)Î Fq [ x ], удовлетворяет условию h (x) q º h (x)(mod f (x)), то
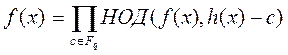 . (7)
. (7)
Доказательство. Каждый НОД из правой части равенства (7) делит многочлен f (x). Поскольку многочлены h (x) – с, c Î Fq попарно взаимно простые, то взаимно простыми являются и их НОД с f (x). Тогда сомножители правой части равенства (7) делят многочлен f (x). С другой стороны, многочлен f (x) делит разность
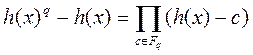 ,
,
а значит f (x) делит правую часть равенства (7). Так как обе части равенства (7) являются нормированными многочленами, каждый из которых делит другой, и значит, они должны совпадать.ÿ
Число различных нормированных неприводимых делителей многочлена f (x) равно k = n – r, где r – ранг матрицы A. Нетривиальные делители многочлена f (x) находим на основании равенства (7) теоремы (2).
Пример 1. Приводим или нет многочлен f (x) = x 4 -2 Î F 3[ x ] над полем F 3 и в случае его приводимости разложить его на множители.
Так как НОД(f (x), f ¢ (x)) = НОД(x 4 -2, x 3) = 1, то имеет место второй случай. Вычислим многочлены a i (x), i =1, 2, 3.
i =1. x 3 – x º x 3 + 2 x (f (x)), a1(x) = 0 + 2 x + 0 x 2 + x 3.
i =2. Так как x 6 º 2 x 2 (f (x)), x 6 – x 2º 4 x 2 º x 2 (f (x)), a2(x) = 0 + 0 x + 1 x 2 + 0 x 3.
i =3. Так как x 5 º 2 x (f (x)), x 9 º 4 x º x (f (x)), x 9 – x 3º x + 2 x 3(f (x)), a3(x) = 0 + 1 x + 0 x 2 + 2 x 3.
Тогда система уравнений (6) принимает вид
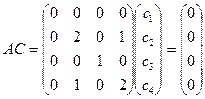 . (7)
. (7)
Так как rang A =2 < 3 = n -1, то многочлен f (x) приводим над полем F 3 и разлагается на произведение k = n – r = 4 – 2 = 2 неприводимых сомножителей.
Общее решение системы (7) С = (с 0, с 1,0, с 1). Поэтому можно выбрать решение с (x) = x 3 + x уравнения (1) По теореме 2
f (x) = x 4 -2 = НОД(x 4 -2, x 3 + x)× НОД(x 4 -2, x 3 + x - 1)× НОД(x 4 -2, x 3 + x - 2).
Находим
НОД(x 4-2, x 3 + x) = 1, НОД(x 4-2, x 3 + x -1) = x 2 + x +2, НОД(x 4-2, x 3 + x -2) = x 2 +2 x +2,.
Отсюда находим
f (x) = (x 2 + x +2)(x 2 +2 x +2).
Так как нетривиальных многочленов в разложении два, то они оба неприводимые над полем Fq.
Так как всего нормированных многочленов степени n над полем Fq имеется (q – 1) qn -1, а неприводимых над полем Fq имеется
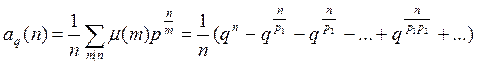 ,
,
то вероятность случайного выбора неприводимого нормированного многочлена равна
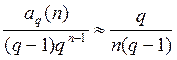 .
.
Число операций необходимых для проверки на неприводимость одного многочлена имеет порядок qn 3. Следовательно, общее число операций имеет порядок (q - 1) n 4.
Существуют более быстрые способы построения неприводимых многочленов с использованием отображений s: Fq [ x ] ® Fq [ x ], t: Fq [ x ] ® Fq [ x ],определяемые формулами:
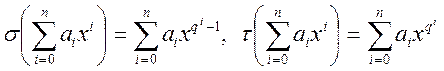 . (8)
. (8)
запишем в виде.
Обозначим, через {a1,…, a s } – множество всех его ненулевых корней в поле разложения над Fq. Через 0(f) обозначим НОК мультипликативных порядков элементов a1,…, a s: 0(f) = НОК(Ord (a1),…, Ord (a s)).
Тогда справедливы теоремы.
Теорема 3. Пусть многочлен f (x)Î Fq [ x ] неприводим над полем Fq, deg f (x) = n, f (x) ¹ x. Тогда многочлен все неприводимы над полем Fq делители многочлена s(f (x)) имеют степень 0(f).
Теорема 4. Пусть многочлен f (x)Î Fq [ x ] неприводим над полем Fq, deg f (x) = n, f (x) ¹ x. Тогда многочлен s(f (x)) неприводим над полем Fq тогда и только тогда, когда 0(f) = qn - 1.
Пример 2. Пусть 2 n – 1 – простое число (простое число Мерсенна). Тогда, если многочлен f (x)Î Fq [ x ] неприводим над полем Fq, deg f (x) = n > 1, то из 0(f)| (2 n – 1) следует, что 0(f) = 2 n – 1 и по теореме 3 многочлен s(f (x)) неприводим над полем Fq.
Так как числа 22– 1 = 3, 23– 1 = 5, 25– 1 = 31, 27– 1 = 127 – простые, то последовательно построим неприводимые над полем F 2многочлены:
f (x) = x 2 + x + 1,
s(f (x)) = x 3 + x + 1,
s2(f (x)) = s(s(f (x))) = x 7 + x + 1,
s3(f (x)) = x 127 + x + 1.
5. Конструкция конечного поля из pn элементов
Пусть f – примитивный многочлен над полем F = Fp степени n, q - один из корней многочлена f в его поле разложения. Тогда простое алгебраическое расширение F (q) – простое поле из pn элементов и каждый элемент этого поля однозначно представим в виде
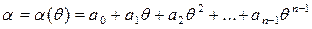 , (1)
, (1)
где a 0, a 1, …, an – 1 – элементы поля F.
С каждым выражение (1) сопоставим n -ку элементов поля F
(a 0, a 1, …, an – 1). (2)
При этом элементы поля F обозначаем значками 0, 1, 2, …, p – 1. Для завершения построения поля из pn элементов укажем, как выполняются операции над n -ками вида (2). Сложение и вычитание выполняется по правилам:
a + b = (a 0, a 1, …, an – 1) + (b 0, b 1, …, bn – 1) = (a 0+ b 0, a 1 + b 1, …, an – 1+ bn – 1),
a - b = (a 0, a 1, …, an – 1) - (b 0, b 1, …, bn – 1) = (a 0- b 0, a 1 - b 1, …, an – 1- bn – 1).
Произведение элементов a, b Î F (q) находим следующим образом. Так как
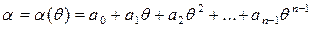 ,
, 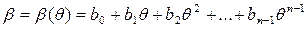 ,
,
то рассмотрим многочлены
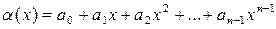 ,
, 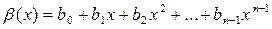 ,
,
и многочлен a(x)×b(x) разделим на многочлен f (x) с остатком:
a(x)×b(x) = f (x) q (x) + g (x), (3)
где 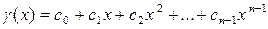 Î F [ x ]. Так как f (q) = 0, то полагая в равенстве (3) x = q получим
Î F [ x ]. Так как f (q) = 0, то полагая в равенстве (3) x = q получим
a(q)×b(q) = f (q) q (q) + g (q) = g (q).
Таким образом,
(a 0, a 1, …, an – 1)× (b 0, b 1, …, bn – 1) = (с 0, с 1, …, с n – 1).
Чтобы найти частное элементов a, b Î F (q)
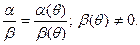 (4)
(4)
Так как многочлен f (x) неприводим над полем F и число q не является корнем многочлена b(x), то многочлены f (x) и b(x) взаимно простые. Тогда найдутся такие два многочлена u (x), v (x) Î F [ x ], что
u (x) f (x) + v (x)b(x) = 1. (5)
Так как f (q) = 0, то полагая в равенстве (5) x = q получим
v (q)b(q) = 1.
Используя это равенство и умножая числитель и знаменатель дроби (5) на v (q) получим
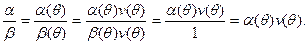
После умножения a (q)v(q) в поле F (q) найдем частное элементов a, b.
Пример 1. Многочлен f (x) = x 2 + x + 1 неприводим над полем F 2, q - один из корней многочлена f в его поле разложения. Тогда простое алгебраическое расширение F 2(q) – простое поле из 22 = 4 элементов и каждый элемент этого поля однозначно представим в виде
 , (6)
, (6)
где a 0, a 1 – элементы поля F 2 = {0, 1}. Таблицы сложения и умножения элементов поля F 2(q) выглядит следующим образом:
| +
| 00
| 01
| 10
| 11
|
| ×
| 00
| 01
| 10
| 11
|
| 00
| 00
| 01
| 10
| 11
|
| 00
| 00
| 00
| 00
| 00
|
| 01
| 01
| 00
| 11
| 10
|
| 01
| 00
| 01
| 01
| 11
|
| 10
| 10
| 11
| 00
| 01
|
| 10
| 00
| 10
| 11
| 01
|
| 11
| 11
| 10
| 01
| 00
|
| 11
| 00
| 11
| 01
| 10
|
6.

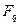 , q = pm, тогда и только тогда, когда выполняются условия:
, q = pm, тогда и только тогда, когда выполняются условия: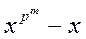 (1)
(1)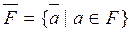 ,
,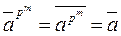 ,
,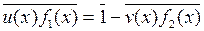 .
.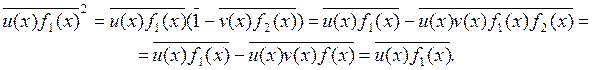
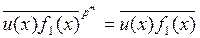
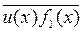 - решение уравнения (1) в кольце R. При этом
- решение уравнения (1) в кольце R. При этом 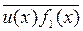 Ï ` F, так как
Ï ` F, так как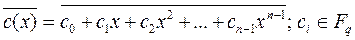 .
.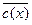 является решением уравнения (1) тогда и только тогда, когда выполняется равенство
является решением уравнения (1) тогда и только тогда, когда выполняется равенство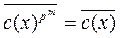 ,
,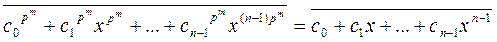 .
.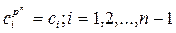 , то отсюда получаем
, то отсюда получаем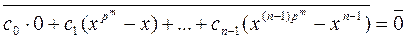 . (3)
. (3)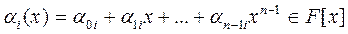 ,
,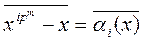 .
.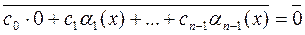 . (4)
. (4)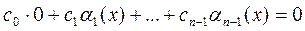 . (5)
. (5)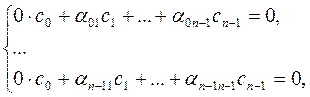
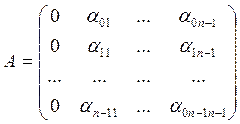 .
.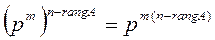 . По теореме 1 многочлен f (x) Î F [ x ] неприводим над полем F =
. По теореме 1 многочлен f (x) Î F [ x ] неприводим над полем F =  , q = pm, тогда и только тогда, когда n -rang A =1, т.е. rang A = n -1.
, q = pm, тогда и только тогда, когда n -rang A =1, т.е. rang A = n -1.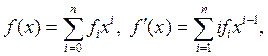
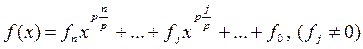
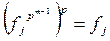
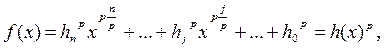
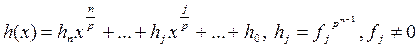 .
.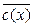 решение уравнения (1), где
решение уравнения (1), где 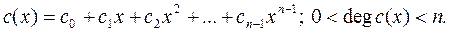
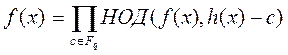 . (7)
. (7)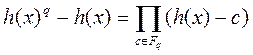 ,
,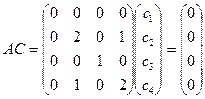 . (7)
. (7)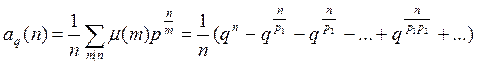 ,
,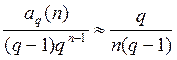 .
.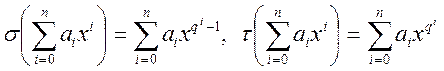 . (8)
. (8)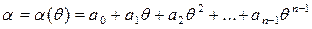 , (1)
, (1)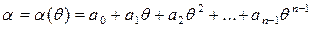 ,
, 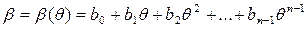 ,
,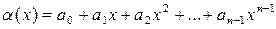 ,
, 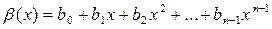 ,
,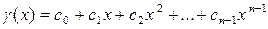 Î F [ x ]. Так как f (q) = 0, то полагая в равенстве (3) x = q получим
Î F [ x ]. Так как f (q) = 0, то полагая в равенстве (3) x = q получим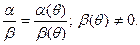 (4)
(4)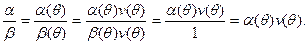
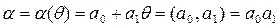 , (6)
, (6)