440305
ПАМ
Толстиков А.В.
Лекция 8. Многочлены над конечными полями
1. Функция Мебиуса и формула обращения Мебиуса.
2. Неприводимые многочлены над конечными полями и их число.
3. Порядок многочлена над конечным полем.
4. Критерий неприводимости многочлена и способы построения неприводимых многочленов над конечным полем.
5. Конструкция конечного поля из pn элементов. Вычисления в конечных полях.
Литература. Нечаев В.И. – С. 34-41, 79-83. С. 42-48.
Глухов М.М. и др. Т.1 – С. 244-251, 262-268; -Т2. –С. 202-220.
С. 221-237.
Самсонов Б.Б., Плохов Е.М., Филоненков А.И. Компьютерная математика (основания информатики). Ростов-на-Дону: «Феникс», 2002. – С. 228-292.
Конечные группы. Примеры конечных групп. Симметрическая группа. Теорема Кэли.
Определение 1. Непустое множество G называется группой, если на множестве G определена бинарная алгебраическая операция, обозначим ее значком умножение, которая каждой паре элементов a, b Î G ставит в соответствие единственный третий элемент из G, обозначаемый ab и для ее выполняются условия:
1) 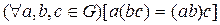 - ассоциативный закон;
- ассоциативный закон;
2) 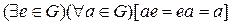 - свойство нейтрального элемента;
- свойство нейтрального элемента;
3) 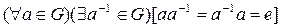 - свойство симметричного элемента.
- свойство симметричного элемента.
Если операция в группе G, как и в нашем случае, обозначается значком «×», то группа G называется мультипликативной, нейтральный элемент называется в этом случае единицей, а симметричный элемент – обратным.
Если операция в группе G обозначается значком «+», то группа G называется аддитивной, нейтральный элемент называется тогда нулем, а симметричный элемент – противоположным.
Если операция в группе G обладает свойством коммутативности, т.е.
 ,
,
то группа G называется коммутативной или абелевой группой
Если число элементов в группе G конечно, то группа G называется конечной группой, если число элементов в группе G бесконечно, то группа G называется бесконечно. В случаеконечной группы число элементов в группе G обозначаем через | G | и называем порядком группы.
Примерами конечных групп являются.
Пример 1. Группа (Z m,+) классов вычетов по модулю m. Порядок этой группы равен m.
Пример 2. Группа (Z m ´,×) примитивных классов вычетов по модулю m. Порядок этой группы равен j(m).
Пример 3. Пусть S = {1, 2,…, n }. Подстановкой n -й степени называемлюбое взаимно однозначное отображение a множества S самого на себя. Любую подстановку a n -й степени можно записать в виде двух n -перестановок, записанных одна под другой, т.е. записать в виде:
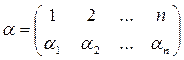 ,
,
где для каждого i Î S a i = a(i).
Если a i = a(i) = i, то говорят, что элемент i переходит при подстановке a в элемент a i. При этом, если a i = i, то элемент i называется неподвижным элементом подстановки a, если a i ¹ i, то элемент i называется подвижным элементом подстановки a.
Композиции подстановок называется умножением подстановок: при умножение подстановок ab нужно сначала выполнить подстановку b, а затем подстановку a. Например, если
 ,
,
то для любого i Î S (ba)(i) = b(a(i)) = b(a i) = b i, т.о.
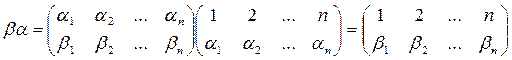 .
.
Подстановки
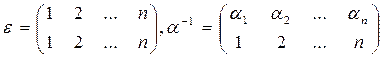
называются соответственно единичной и обратной подстановкой для a.
Множество всех подстановок n -й степени обозначается символом Sn.
Справедлива теорема.
Теорема 1. Множество Sn всех подстановок -й степени образует группу относительно операции умножения подстановок. ÿ
Группа Sn играет большую роль в математике и называется симметрической группой подстановок n -й степени.
Особое положение теории групп подстановок в теории групп поясняется следующей теоремой.
Теорема 2 (Кэли). Любая конечная группа G порядка n изоморфна некоторой подгруппе симметрической группы n -й степени Sn.
Доказательство. Пусть G = { a 1, a 2,…, an }, a 1 = e - единичный элемент группы G. Рассмотрим n-ку (a 1, a 2,…, an). Возьмем произвольный элемент a Î G, и рассмотрим n-ку (aa 1, aa 2,…, aan). Все элементы этого множества принадлежат G и попарно различны. Действительно, если aai = aaj, то по закону сокращения получаем ai = aj противоречие с тем, что все элементы множества { a 1, a 2,…, an } попарно различны. Таким образом, n -ка (aa 1, aa 2,…, aan) определяется однозначно и является перестановкой из элементов группы G, (aa 1, aa 2,…, aan) = =  . Обозначим ее через j(a) подстановку n -степени
. Обозначим ее через j(a) подстановку n -степени 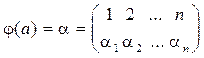 , которая по элементу определяется однозначно. Покажем, что, если a, b Î G, a ¹ b, то j(a) ¹ j(b). Действительно, если a ¹ b, то для любого элемента ai Î G aai ¹ bai. Поэтому элементам a, b соответствуют различные перестановки j(a), j(b). В В силу сказанного выше j - взаимно однозначное отображение G группы в группу Sn.
, которая по элементу определяется однозначно. Покажем, что, если a, b Î G, a ¹ b, то j(a) ¹ j(b). Действительно, если a ¹ b, то для любого элемента ai Î G aai ¹ bai. Поэтому элементам a, b соответствуют различные перестановки j(a), j(b). В В силу сказанного выше j - взаимно однозначное отображение G группы в группу Sn.
Покажем, что установленное соответствие является изоморфизмом группы G на подалгебру j(G) группы Sn..Покажем, что для любых двух элементов a, b Î G имеет место равенство j(ab) = j(a)j(b). Пусть
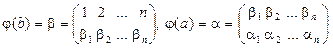 .
.
Тогда по определению произведения подстановок
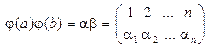 . (1)
. (1)
По определению установленного выше соответствия j имеем
(ba 1, ba 2,…, ban) = 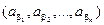 ,
, 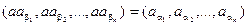 .
.
Тогда в силу ассоциативного закона будем иметь
((ab) a 1, (ab) a 2,…, (ab) an) =(a (ba 1), a (ba 2),…, a (ban))= 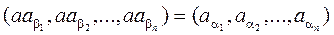
По определению установленного выше соответствия j и формулы (1) получаем
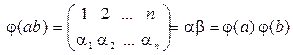 .
.
Так как отображение j является изоморфизмом алгебр G и j(G), и G группа, то j(G) группа. Таким образом, G изоморфно подгруппе j(G) группы Sn.
Следствие. Все конечные группы порядка n с точностью до изоморфизма являются подгруппами симметрической группы Sn подстановок n -й степени.
Определение 2. Подстановку aÎ Sn не равная единичной называют циклом длины k, если она перестановкой столбцов, может быть приведена к виду:
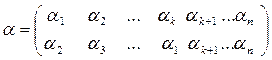 ,
,
т.е. элементы a1, a2,…, a k подстановки переставляются по циклу, а остальные элементы остаются на своих местах.
Для записи цикла удобна более простая запись подстановки:
a = (a1, a2,…, a k).
Заметим, что один и тот же цикл длины k можно записать k способами.
Два цикла называются независимыми, если они не содержат одинаковых элементов.
Теорема 3. Любая неединичная подстановка aÎ Sn либо является циклом, либо раскладывается в произведение некоторого числа попарно независимых циклов. Такое разложение однозначно с точностью до порядка следования сомножителей.
Доказательство. Доказательство существования проведем методом математической индукции по числу m подвижных элементов в подстановке a. Число подвижных элементов в неединичной подстановке a не менее двух. Пусть m = 2. Тогда в подстановке a два подвижных элемента a1 и a2 , которые образуют цикл длины 2 и подстановка a – цикл a = (a1, a2). Для m = 2 утверждение теоремы справедливо.
Допустим, что утверждение теоремы справедливо для любой подстановки, которая имеет менее m подвижных элементов и докажем его для подстановки a, имеющей m подвижных элементов. Пусть a1 – любой подвижный элемент подстановки a. Тогда имеем последовательность элементов
a2 = a(a1), a3 = a(a2) = a2(a1), a4 = a(a3)= a3(a1),…, a i = a(a i - 1)= a i -1(a1),… (1)
Так как все элементы последовательности (1) принадлежат S, то среди них обязательно найдется по крайней мере два равных:
a i = a j, (i < j), т.е. a i -1(a1) = a j -1(a1).
Применяя к обеим частям последнего равенства подстановку (a-1) i -1 получаем
. a j - i (a1) = e(a1) = a1.
Таким образом, в последовательности (1) найдется элемент a i; i > 1, равный элементу a1. Пусть k - наименьшее натуральное число > 1 с таким свойством.
Рассмотрим цикл b = (a1, a2, …, a k - 1). Тогда подстановка b-1a оставляет элементы a1, a2, …, a k - 1 неподвижными и сохраняет неподвижные элементы подстановки a. Тогда число неподвижных элементов в подстановке b-1a меньше m и к ней применимо индуктивное предположение b-1a представляется в виде произведения независимых циклов, в которые войдут только подвижные элементы подстановки b-1a: b-1a = g…d. Отсюда a = bg…d. Тогда первая часть теоремы доказана.
Методом от противного доказывается единственность разложения.
Пример 1.
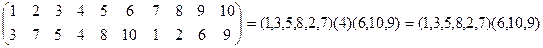 .
.
Доказательство.
1) Следует из равенства (1).
2) Следует из того, что порядок элемента конечной группы является делителем порядка группы.
3) Следует из того, что q – 1 делит qn – 1.
4) Для a = 0 очевидно, а для a ¹0 следует из 3).ÿ
Теорема 2. Для любого элемента a Î Fq * порядка d выполняются свойства:
10 для любых натуральных чисел a m = a k тогда и только тогда, когда m º k (mod d);
20 все элементы множества
1, a, a 2, …, a d-1 (3)
различны;
30 элементы множества (3) есть все корни многочлена
x d - 1; (4)
40 для любого натурального числа k порядок элемента ak равен 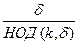 .
.
50 для любого натурального числа k ord ak = d тогда и только тогда, когда числа k и d взаимно простые;
60 число элементов b Î Fq порядка d равно j(d).
Доказательство. Свойства 10 и 20 следуют из свойства порядка элемента мультипликативной группы.
30 Так как для любого натурального числа k
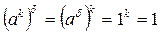 ,
,
то все элементы множества (3) являются корнями многочлена (4). Так как многочлен степени d над полем Fq имеет не более d корней, то все корни многочлена (4) исчерпываются элементами множества (3).
40 Пусть ord ak = m. Тогда
 .
.
Тогда по следствию теоремы Лагранжа d делит km. Поэтому
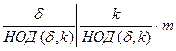 .
.
Так как числа
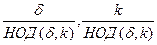
взаимно простые, то
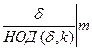 . (5)
. (5)
С другой стороны,
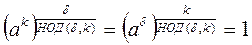 .
.
Поэтому
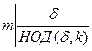 . (6)
. (6)
Из (5) и (6) следует, что
 . (7)
. (7)
50 Пусть числа k иd взаимно простые. Тогда НОД(k, d) = 1 и из формулы (7) следует, что ord ak = d. Обратно, если ord ak = d, то из формулы (7) следует, что НОД(k, d) = 1 и числа k иd взаимно простые.
60 По определению всяких элемент b порядка d корень уравнения (4). По свойству 30 все корни уравнения (4) исчерпываются элементами множества (3). По свойству 50 элемент ak из множества (3) имеет порядок k тогда и только тогда, когда (k, d) = 1. Таким образом, элементов порядка d в поле Fq столько, сколько во множестве {0, 1, …, d -1} имеется чисел взаимно простых с числом d. По определению функции Эйлера таких чисел j(d). Следовательно, в поле Fq имеется j(d) элементов, имеющих порядок d.ÿ
6.
Выписывается элемент 1.
2. Умножается полученный элемент на x.
Переход к пункту 2.
Пример 3. Генерировать все элементы поле 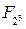 , f (x) = x 3 + x + 1 в полиномиальном представлении:
, f (x) = x 3 + x + 1 в полиномиальном представлении:
1, x, x 2 , x 3 = x + 1, x 4= x (x + 1) = x 2 + x, x 5= x (x 2 + x) = x 3 + x 2 = x 2 + x + 1,
x 6= x (x 2 + x + 1) = x 3 + x 2 + 1= x 2 + x.
При векторном и полиномиальном представлении элементов поля сложение и вычитание выполняются естественным образом как поразрядное сложение и соответственно вычитание по модулю p. При полиномиальном представлении элементов умножении элементов поля осуществляется по следующему алгоритму:
440305
ПАМ
Толстиков А.В.
Лекция 8. Многочлены над конечными полями
1. Функция Мебиуса и формула обращения Мебиуса.
2. Неприводимые многочлены над конечными полями и их число.
3. Порядок многочлена над конечным полем.
4. Критерий неприводимости многочлена и способы построения неприводимых многочленов над конечным полем.
5. Конструкция конечного поля из pn элементов. Вычисления в конечных полях.
Литература. Нечаев В.И. – С. 34-41, 79-83. С. 42-48.
Глухов М.М. и др. Т.1 – С. 244-251, 262-268; -Т2. –С. 202-220.
С. 221-237.
Самсонов Б.Б., Плохов Е.М., Филоненков А.И. Компьютерная математика (основания информатики). Ростов-на-Дону: «Феникс», 2002. – С. 228-292.
Конечные группы. Примеры конечных групп. Симметрическая группа. Теорема Кэли.
Определение 1. Непустое множество G называется группой, если на множестве G определена бинарная алгебраическая операция, обозначим ее значком умножение, которая каждой паре элементов a, b Î G ставит в соответствие единственный третий элемент из G, обозначаемый ab и для ее выполняются условия:
1) 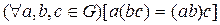 - ассоциативный закон;
- ассоциативный закон;
2) 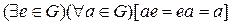 - свойство нейтрального элемента;
- свойство нейтрального элемента;
3) 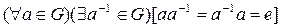 - свойство симметричного элемента.
- свойство симметричного элемента.
Если операция в группе G, как и в нашем случае, обозначается значком «×», то группа G называется мультипликативной, нейтральный элемент называется в этом случае единицей, а симметричный элемент – обратным.
Если операция в группе G обозначается значком «+», то группа G называется аддитивной, нейтральный элемент называется тогда нулем, а симметричный элемент – противоположным.
Если операция в группе G обладает свойством коммутативности, т.е.
 ,
,
то группа G называется коммутативной или абелевой группой
Если число элементов в группе G конечно, то группа G называется конечной группой, если число элементов в группе G бесконечно, то группа G называется бесконечно. В случаеконечной группы число элементов в группе G обозначаем через | G | и называем порядком группы.
Примерами конечных групп являются.
Пример 1. Группа (Z m,+) классов вычетов по модулю m. Порядок этой группы равен m.
Пример 2. Группа (Z m ´,×) примитивных классов вычетов по модулю m. Порядок этой группы равен j(m).
Пример 3. Пусть S = {1, 2,…, n }. Подстановкой n -й степени называемлюбое взаимно однозначное отображение a множества S самого на себя. Любую подстановку a n -й степени можно записать в виде двух n -перестановок, записанных одна под другой, т.е. записать в виде:
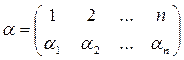 ,
,
где для каждого i Î S a i = a(i).
Если a i = a(i) = i, то говорят, что элемент i переходит при подстановке a в элемент a i. При этом, если a i = i, то элемент i называется неподвижным элементом подстановки a, если a i ¹ i, то элемент i называется подвижным элементом подстановки a.
Композиции подстановок называется умножением подстановок: при умножение подстановок ab нужно сначала выполнить подстановку b, а затем подстановку a. Например, если
 ,
,
то для любого i Î S (ba)(i) = b(a(i)) = b(a i) = b i, т.о.
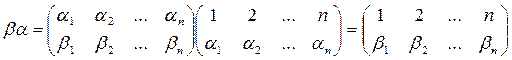 .
.
Подстановки
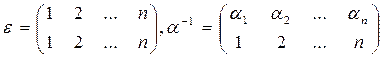
называются соответственно единичной и обратной подстановкой для a.
Множество всех подстановок n -й степени обозначается символом Sn.
Справедлива теорема.
Теорема 1. Множество Sn всех подстановок -й степени образует группу относительно операции умножения подстановок. ÿ
Группа Sn играет большую роль в математике и называется симметрической группой подстановок n -й степени.
Особое положение теории групп подстановок в теории групп поясняется следующей теоремой.
Теорема 2 (Кэли). Любая конечная группа G порядка n изоморфна некоторой подгруппе симметрической группы n -й степени Sn.
Доказательство. Пусть G = { a 1, a 2,…, an }, a 1 = e - единичный элемент группы G. Рассмотрим n-ку (a 1, a 2,…, an). Возьмем произвольный элемент a Î G, и рассмотрим n-ку (aa 1, aa 2,…, aan). Все элементы этого множества принадлежат G и попарно различны. Действительно, если aai = aaj, то по закону сокращения получаем ai = aj противоречие с тем, что все элементы множества { a 1, a 2,…, an } попарно различны. Таким образом, n -ка (aa 1, aa 2,…, aan) определяется однозначно и является перестановкой из элементов группы G, (aa 1, aa 2,…, aan) = =  . Обозначим ее через j(a) подстановку n -степени
. Обозначим ее через j(a) подстановку n -степени 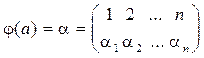 , которая по элементу определяется однозначно. Покажем, что, если a, b Î G, a ¹ b, то j(a) ¹ j(b). Действительно, если a ¹ b, то для любого элемента ai Î G aai ¹ bai. Поэтому элементам a, b соответствуют различные перестановки j(a), j(b). В В силу сказанного выше j - взаимно однозначное отображение G группы в группу Sn.
, которая по элементу определяется однозначно. Покажем, что, если a, b Î G, a ¹ b, то j(a) ¹ j(b). Действительно, если a ¹ b, то для любого элемента ai Î G aai ¹ bai. Поэтому элементам a, b соответствуют различные перестановки j(a), j(b). В В силу сказанного выше j - взаимно однозначное отображение G группы в группу Sn.
Покажем, что установленное соответствие является изоморфизмом группы G на подалгебру j(G) группы Sn..Покажем, что для любых двух элементов a, b Î G имеет место равенство j(ab) = j(a)j(b). Пусть
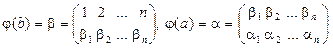 .
.
Тогда по определению произведения подстановок
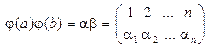 . (1)
. (1)
По определению установленного выше соответствия j имеем
(ba 1, ba 2,…, ban) = 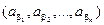 ,
, 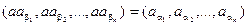 .
.
Тогда в силу ассоциативного закона будем иметь
((ab) a 1, (ab) a 2,…, (ab) an) =(a (ba 1), a (ba 2),…, a (ban))= 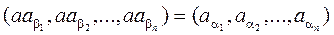
По определению установленного выше соответствия j и формулы (1) получаем
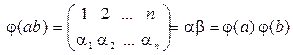 .
.
Так как отображение j является изоморфизмом алгебр G и j(G), и G группа, то j(G) группа. Таким образом, G изоморфно подгруппе j(G) группы Sn.
Следствие. Все конечные группы порядка n с точностью до изоморфизма являются подгруппами симметрической группы Sn подстановок n -й степени.
Определение 2. Подстановку aÎ Sn не равная единичной называют циклом длины k, если она перестановкой столбцов, может быть приведена к виду:
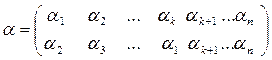 ,
,
т.е. элементы a1, a2,…, a k подстановки переставляются по циклу, а остальные элементы остаются на своих местах.
Для записи цикла удобна более простая запись подстановки:
a = (a1, a2,…, a k).
Заметим, что один и тот же цикл длины k можно записать k способами.
Два цикла называются независимыми, если они не содержат одинаковых элементов.
Теорема 3. Любая неединичная подстановка aÎ Sn либо является циклом, либо раскладывается в произведение некоторого числа попарно независимых циклов. Такое разложение однозначно с точностью до порядка следования сомножителей.
Доказательство. Доказательство существования проведем методом математической индукции по числу m подвижных элементов в подстановке a. Число подвижных элементов в неединичной подстановке a не менее двух. Пусть m = 2. Тогда в подстановке a два подвижных элемента a1 и a2 , которые образуют цикл длины 2 и подстановка a – цикл a = (a1, a2). Для m = 2 утверждение теоремы справедливо.
Допустим, что утверждение теоремы справедливо для любой подстановки, которая имеет менее m подвижных элементов и докажем его для подстановки a, имеющей m подвижных элементов. Пусть a1 – любой подвижный элемент подстановки a. Тогда имеем последовательность элементов
a2 = a(a1), a3 = a(a2) = a2(a1), a4 = a(a3)= a3(a1),…, a i = a(a i - 1)= a i -1(a1),… (1)
Так как все элементы последовательности (1) принадлежат S, то среди них обязательно найдется по крайней мере два равных:
a i = a j, (i < j), т.е. a i -1(a1) = a j -1(a1).
Применяя к обеим частям последнего равенства подстановку (a-1) i -1 получаем
. a j - i (a1) = e(a1) = a1.
Таким образом, в последовательности (1) найдется элемент a i; i > 1, равный элементу a1. Пусть k - наименьшее натуральное число > 1 с таким свойством.
Рассмотрим цикл b = (a1, a2, …, a k - 1). Тогда подстановка b-1a оставляет элементы a1, a2, …, a k - 1 неподвижными и сохраняет неподвижные элементы подстановки a. Тогда число неподвижных элементов в подстановке b-1a меньше m и к ней применимо индуктивное предположение b-1a представляется в виде произведения независимых циклов, в которые войдут только подвижные элементы подстановки b-1a: b-1a = g…d. Отсюда a = bg…d. Тогда первая часть теоремы доказана.
Методом от противного доказывается единственность разложения.
Пример 1.
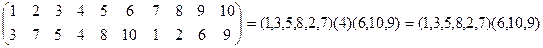 .
.


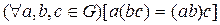 - ассоциативный закон;
- ассоциативный закон;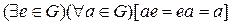 - свойство нейтрального элемента;
- свойство нейтрального элемента;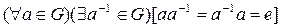 - свойство симметричного элемента.
- свойство симметричного элемента. ,
,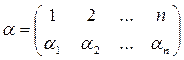 ,
, ,
,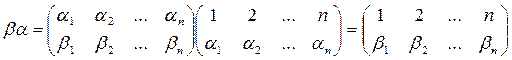 .
.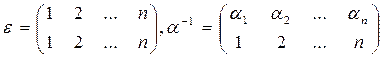
 . Обозначим ее через j(a) подстановку n -степени
. Обозначим ее через j(a) подстановку n -степени 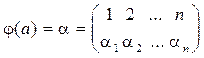 , которая по элементу определяется однозначно. Покажем, что, если a, b Î G, a ¹ b, то j(a) ¹ j(b). Действительно, если a ¹ b, то для любого элемента ai Î G aai ¹ bai. Поэтому элементам a, b соответствуют различные перестановки j(a), j(b). В В силу сказанного выше j - взаимно однозначное отображение G группы в группу Sn.
, которая по элементу определяется однозначно. Покажем, что, если a, b Î G, a ¹ b, то j(a) ¹ j(b). Действительно, если a ¹ b, то для любого элемента ai Î G aai ¹ bai. Поэтому элементам a, b соответствуют различные перестановки j(a), j(b). В В силу сказанного выше j - взаимно однозначное отображение G группы в группу Sn.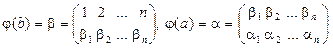 .
.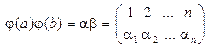 . (1)
. (1)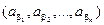 ,
, 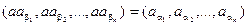 .
.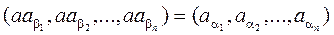
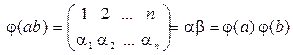 .
.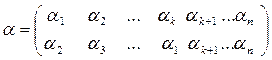 ,
,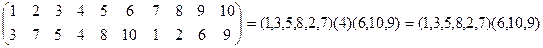 .
.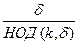 .
.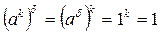 ,
, .
.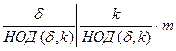 .
.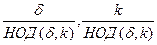
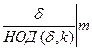 . (5)
. (5)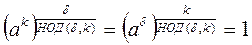 .
.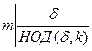 . (6)
. (6) . (7)
. (7) , f (x) = x 3 + x + 1 в полиномиальном представлении:
, f (x) = x 3 + x + 1 в полиномиальном представлении:


