Дискретное логарифмирование
План.
1. Показатели по модулю и их свойства.
2. Первообразные корни их существование и свойства
3. Индексы и их свойства. Определение дискретного логарифма
4. Квадратичные сравнения. Символы Лежандра и Якоби и их свойства.
5. Первообразные корни их существование и свойства
6. Индексы и их свойства. Определение дискретного логарифма
7. Алгоритм Диффи-Хелмана.
8. Криптосистема Эль-Гамаля.
9. Криптосистема Рабина.
10. Криптосистема Шамира.
Показатели по модулю и их свойства.
Определение 1. Пусть (a, m) =1. Порядком или показателем числа a по модулю m называется такое наименьшее натуральное число a, что
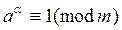 . (1)
. (1)
Обозначаем порядок числа a по модулю m через Pm (a). Порядок по модулю обладает следующими свойствами.
10 Если (a, m) =1 то Pm (a) существует и Pm (a) £. j(a).
20 Если (a, m) =1 и b º a (mod m), то Pm (b) = Pm (a).
30 Если d = Pm (a) и 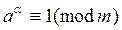 , то d|a.
, то d|a.
40 Если d = Pm (a), то d|j(m).
50 Если (a, m) =1 и d = Pm (a), 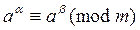 , то aºb(mod d).
, то aºb(mod d).
60 Если (a, m) =1 и d = Pm (a), то все степени 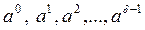 попарно несравнимы по модулю m..
попарно несравнимы по модулю m..
Алгоритм нахождения показателя r = Pm (a).
Ввод: Проверяемое число a и модуль m..
m:=0; r:= b;a 1:= a;;b 1:= b;
d:= function НОД (a, m);
if d >1 then s $:= «показатель Pm (a) не существует»
else P:=1; (q, r): = div (a, m);
while r ¹ 1 do P:= P + 1; (q, r): = div (ra, m); end while;
s $:= «показатель Pm (a) равен»;
end if
Вывод: s $и P.
Так как по свойству 40 порядок числа Pm (a) делит число j(m), то найдя каноническое разложение числа j(m) можно перебирать только делители числа j(m). Тогда алгоритм вычисления показателя принимает следующий вид.
Алгоритм нахождения показателя r = Pm (a).
Ввод: Проверяемое число a и модуль m..
m:=0; r:= b;a 1:= a;;b 1:= b;
d:= function НОД (a, m);
if d >1 then s $:= «показатель Pm (a) не существует»
else
f: = function j(m)
procedure Факторизация(f; A, k);{A- матрица, имеющая две строки, в первой строка матрицы, простые числа, делящие число m, вторая – соответствующие показатели этих простых чисел в каноническом разложении числа f, k – число различных простых множителей в каноническом разложении числа f }
d:=1; (q, r): = div (a, m);
for i:= 1 to k; B (i, 1):=1; B (i, 2):=0; end for; i:=1;
while r ¹ 1 do d:= d + 1; (q, r): = div (ra, m);
r:=0; {Перебор делителей числа j(m) до тех пор пока не будет r = 1}
while r = 0 do
if B (i, 2) < A (i, 2) then
B (i, 2):= B (i, 2) +1; p:= A (i, 2); v:= a;
while p > 0 do
(p, u):= div (p,2)
if u = 1 then (q, B (i, 1)):= div (B (i, 1)* v, m); end if
( q, v):= div (v* v, m);
end while;
r:= B (i, 1);
while i > 1 do i:=i- 1; B (i, 1):= r; B (i, 2):=0; end while;
else
i:=i+ 1;
end while;
end while;
P:=1;
for i:= 1 to k;
while B (i, 2)> 0 do P:= P*A (i, 1); B (i, 2):= B (i, 2)-1; end while;
end for;
s $:= «показатель Pm (a) равен»; P;
end if.
Вывод: s $и r.
Пример 2. Найти показатель числа 7 по модулю 15. Так как (7, 15) =1, то показатель существует. Вычисляем j(15) = 2×4 = 8. Делители числа j(15);1, 2, 4, 8.
Так как 7T1(mod 15), 72 º 49 º 4 T1(mod 15), 74 º 42 º1(mod 15), то P 15(7) = 4.
End while
End while
End while
End while
End while
End while
Вывод: p и K, P, a.
Нахождение первообразного корня g по модулю p простого числа типа Жермен.
Ввод: p – простое число, K, P – факторизация числа p -1
g:=1;pr:=0;
while pr=0 do
g:=g+1; i:=0
while k[i]>0 and pr=0 and i<6 do;
if BigStMod(g,(p-1)/P[i],p) =1 then pr:=0; i:=7; else i:=i+1;end if;
if i=6 then pr:=1;end if;
end while
end while;
Вывод: g.
Алгоритм Диффи-Хелмана.
Создание общего секретного ключа для КС с секретным ключом.
Рассмотрим случай двух абонентов A и B.
1. Один из абонентов, например A определяет большое число p и вычисляет для него первообразный корень g.
2. Абонент A пересылает по открытому каналу числа p, g абоненту B.
3. Абонент A выбирает случайное число a, 1< a < p -1 и вычисляет число с º ga (mod p).
4. Абонент B выбирает случайное число b, 1< b < p -1 и вычисляет число d º gb (mod p).
5. Абонент A пересылает по открытому каналу число с абоненту B.
6. Абонент B пересылает по открытому каналу число d абоненту A.
7. Абонент A вычисляет число k 1º da (mod p), 0< k 1< p.
8. Абонент B вычисляет число k 2º cb (mod p), 0< k 2< p.
Так как k 1º da º (gb) a º gba º gab º (ga) b º cb º k 2 (mod p), и 0< k 1< p, 0< k 2< p, то 0< k 1= k 2. Следовательно, абоненты A и B получили общий секретный ключ k = k 1= k 2., который не пересылался по открытому каналу связи.
Крипто аналитику необходимо по числам p, g, c, d, пересылаемым по открытым каналам связи необходимо вычислить общий секретный ключ, а для этого ему будет необходимо вычислить числа a или b, т.е. вычислить a º ind g c (mod p -1) или b º ind g d (mod p -1). Последнее связано с решение трудной задачи «Проблемы дискретного логараифма».
Потребуются программы:
Возведение целого числа в степень по модулю.
Программа вычисления простого числа Жермен.
Программа вычисления первообразного корня для простого числа Жермен.
Криптосистема Эль-Гамаля.
Генерация ключей.
Для группы пользователей выбирается большое число p (простое число С.Жермен) и вычисляет для него первообразный корень g.
Получатель секретного сообщения, например, B производит генерацию открытого ключа и закрытого ключа:
1) выбирает секретное число с;
2) вычисляет соответствующее ему открытое число d: d º gc (mod p), 0< d < p;
3) определяет закрытый (секретный) ключ (p, g, c), оставляя его себе;
4) открытый ключ ((p, g, d)) сообщаются всем отправителям сообщений.
Шифрование
- Шифруемое сообщение представляется в виде последовательности чисел X 1, X 2,… (0≤ Xi < p, i =1.2,…)
2 Каждый блок Xi, i =1.2,… шифруется по правилу:
1) формируется случайное число k; 0< k < p -1;
2) вычисляется число
Yi º g k (mod p), 0< Yi < p, (1)
3) вычисляется число
Zi º Xi d k (mod p), 0< Zi < p, (2)
- Получателю B отправляется последовательность чисел Y 1, Z 1, Y 2, Z 2,…., которая представляет собой зашифрованное сообщение.
Расшифровывание.
Зашифрованное сообщение Y 1, Z 1, Y 2, Z 2,…., расшифровывается по правилу:
Xi’ º Z i Yi - c º Z i Yi p -1- c (mod p), (3)
Ниже доказывается, что полученная последовательность чисел X 1’, X 2’,… (0≤ Xi ’ < p, i =1.2,…), совпадает с исходной последовательностью X 1, X 2,…, которая преобразуется в исходный текст.
Теорема 1. Шифрование с открытым ключом корректно, т.е. в предыдущих обозначениях Xi ’= Xi.
Доказательство. Из (1), (2), (3) получаем
Xi’ º Z i Yi - c º Z i Yi p -1- c º Xi (gc) k (g k) p -1- c º Xi gc k g k (p -1)- kc º Xi (g p -1) k º Xi (mod p).
Так как 0≤ Xi < p и 0≤ Xi ’ < p, то Xi ’= Xi для всех i =1.2,….
Сложностью крипто анализа в КС Эль-Гамаля является сложность решения проблемы дискретного алгоритма.
Потребуются программы.
Возведение целого числа в степень по модулю.
Программа вычисления простого числа Жермен.
Программа вычисления первообразного корня для простого числа Жермен.
Программа преобразования текста в числа с основанием счисления p.
Программа преобразования числа с основанием счисления p в текст.
Написать программы.
Программа генерации ключей El-Gamalia.
Программа решения линейного сравнения по модулю.
Программа шифрования El-Gamalia.
Программа расшифровывания El-Gamalia.
.
Криптосистема Шамира.
Шифр Шимира позволяет передавать сообщения по открытым каналам связи, когда нет никаких ни открытых ни секретных ключей, которые нужно передавать друг другу.
Пусть два абонента A и B соединены открытой линией связи. Пусть A хочет передать сообщение T абоненту B так, чтобы никто не узнал его содержимого.
1. A выбирает случайное большое простое число p и пересылает его по открытому каналу связи B.
2. A выбирает случайное большое число a взаимно простое с p -1 1< a < p -1 и вычисляет число с, решая сравнение ac º 1 (mod p -1), 1< c < p -1.
3. B выбирает случайное большое число b взаимно простое с p -1 1< b < p -1 и вычисляет число d, решая сравнение bd º 1 (mod p -1), 1< d < p -1.
Передаваемое сообщение представляется в виде последовательности чисел X 1, X 2,… (0≤ Xi < p, i =1.2,…). При этом для кодирования каждого из чисел Xi лучше выбирать случайно новые пары (a, c) и (b, d).
В настоящее время такой шифр, как правило используется для передачи чисел, меньших p, например, для передачи секретных ключей.
Опишем протокол передачи каждого из чисел Xi
1. A выбирает пару (a, c).
2. A вычисляет число Yi º Xi a (mod p), 0< Yi < p, и пересылает его B.
3. B выбирает пару (b, d).
4. B вычисляет число Zi º Yi b (mod p), 0< Zi < p, и пересылает его A.
5. A вычисляет число Ui º Zi c (mod p), 0< Ui < p, и пересылает его B.
6. B вычисляет число Vi º Ui d (mod p), 0< Vi < p (ниже доказывается, что число Vi совпадает с числом Xi.
Теорема. 1) В результате реализации протокола Шамира получим Vi = Xi.
2) крипто аналитик не может узнать, какое сообщение было передано.
Доказательство. Из условий под пар (a, c) и (b, d) следует, что
ac = 1 + k (p -1), bd = 1 + l (p -1), где k, l Î Z.
Тогда при Xi делящемся на p имеем Vi = Xi =0, а при Xi не делящемся на p имеем
Vi º Ui d º (Zi c) d º Zi cd º (Yi b) cd º (Yi bd) c º (Yi 1+ 1(p- 1)) c º (Yi (Yi p- 1) l) c º (Yi) c º (Xi a) c º º Xi ac º Xi 1 + k (p -1) º Xi Xi (p -1) k º Xi (mod p),
Так как 0≤ Xi < p и 0≤ Vi < p, то Vi = Xi для всех i =1.2,….
Доказательство второго утверждения основано на предположении, что злоумышленник, пытающийся определить Xi должен сначала определить c, из условия Ui º Zi c (mod p), 0< Zi < p, затем вычислить Xi из условия Yi c º Xi ac º Xi (mod p), 1< Xi < p.
Потребуются программы.
Возведение целого числа в степень по модулю.
Программа преобразования текста в числа с основанием счисления p.
Программа преобразования числа с основанием счисления p в текст.
Криптосистема Рабина.
Криптосистема Рабина, используя в качестве шифрования возведение в квадрат по модулю. Пусть два абонента A и B соединены открытой линией связи. Пусть A хочет передать сообщение T абоненту B так, чтобы никто не узнал его содержимого.
Генерация ключей.
1. B выбирает случайно два различные большие простое число p и q. Эти числа представляют секретный ключ. Удобно выбирать p º 3 (mod 4), q º 3 (mod 4).
- Тогда открытый ключ представляет произведение n = pq.
Шифрование.
1. Передаваемое сообщение представляется в виде последовательности чисел X 1, X 2,… (0≤ Xi < n, i =1.2,…).
- Каждое Xi шифруется по формуле Yi º Xi 2(mod n), 0≤ Yi < n.
- Последовательность чисел Y 1, Y 2, …. пересылается B.
Расшифровывание.
Расшифровывание полученной последовательности Y 1, Y 2, …. состоит в решении для
каждого Yi квадратичного сравнения
Yi º X 2(mod n). (4)
Для B, знающего разложение числа n = pq, это сравнение равносильно системе сравнений
Yi º X 2(mod p), (5)
Yi º X 2(mod q). (6)
Тогда при Xi делящемся на p имеем X º Vi º Xi º0(mod p), а при Xi не делящемся на p имеем.
Так как p º 3 (mod 4), то решение X сравнения (5) можно найти по формул X º Yi ( p +1)/4(mod p). Действительно,
X 2º Yi (p +1)/2º Yi Yi (p- 1)/2 º Yi Xi (p- 1) º Yi (mod p).
Таким образом, для каждого из сравнений (5) и (6) мы можем найти по два решения
X º ± Yi (p +1)/4(mod p), X º ± Yi (q +1)/4(mod q).
Тогда, используя китайскую теорему об остатках найдем 4 решения сравнения (4). Возникает неоднозначность расшифровывания. Если открытое сообщение обладает некоторой избыточностью, например, написано на естественном языке, то это не должно стать помехой для расшифровывания.
такой шифр, как правило используется для передачи чисел, меньших p, например, для передачи секретных ключей.
Теорема. 1) В результате реализации протокола Рабина получим X = Xi.
2) крипто аналитик не может узнать, какое сообщение было передано.
Доказательство. Первая часть утверждения была обоснована выше.
Если крипто аналитик не зная разложение числа n на простые множители, то он может решить сравнение (4) только перебором. Поэтому, для того, чтобы решить сравнение (4) необходимо знать разложение числа n на простые множители. Последняя задача трудно решаемая и связана с проблемой разложения целого числа на простые множители.
Потребуются программы.
Возведение целого числа в степень по модулю.
Программа вычисления простого числа
Программа преобразования текста в числа с основанием счисления p.
Программа преобразования числа с основанием счисления p в текст.
Написать программы.
Программа генерации ключей Рабина.
Программа решения линейного сравнения по модулю.
Программа реализующая китайскую теорему об остатках.
Программа шифрования Рабина.
Программа расшифровывания Рабина.
Вопросы.
1. Определение показателя числа по модулю.
2. Свойства показателя числа по модулю.
3. Алгоритм вычисления показателя числа по модулю.
4. Определение первообразного корня.
5. Условие существования первообразного корня.
6. Число первообразных корней в полной системе вычетов по модулю.
7. Алгоритм нахождения первообразного корня.
8. Алгоритм подбора большого простого числа Жермен для вычисления его первообразного корня.
9. Определение индекса (дискретного логарифма) числа по модулю.
10. Свойства индексов.
11. Вычисление индексов.
12. Определение квадратичного вычета по модулю.
13. Определение символа Лежандра.
14. Теорема Эйлера.
15. Свойства Символа Лежандра. Квадратичный закон взаимности.
16. Вычисление символа Лежандра.
17. Символ Якоби и его свойства.
18. Алгоритм Деффи-Хеллмана.
19. Крипто система Эль-Гамаля. Генерация ключей. Шифрование и расшифровывание.
20. Криптосистема Шамира. Генерация ключей. Шифрование и расшифровывание.
21. Криптосистема Рабина. Генерация ключей. Шифрование и расшифровывание.
22. Теорема Эйлера и возможность ее использования для тестирования простых чисел на простоту.
23. Псевдопростые числа Эйлера.
24. Что такое криптосистема? Основные задачи криптографии.
25. Криптографический алгоритм. Криптографический протокол.
26. Принцип Керкгоффса.
27. Уязвимости RSA относительно активных и пассивных атак.
Дискретное логарифмирование
План.
1. Показатели по модулю и их свойства.
2. Первообразные корни их существование и свойства
3. Индексы и их свойства. Определение дискретного логарифма
4. Квадратичные сравнения. Символы Лежандра и Якоби и их свойства.
5. Первообразные корни их существование и свойства
6. Индексы и их свойства. Определение дискретного логарифма
7. Алгоритм Диффи-Хелмана.
8. Криптосистема Эль-Гамаля.
9. Криптосистема Рабина.
10. Криптосистема Шамира.
Показатели по модулю и их свойства.
Определение 1. Пусть (a, m) =1. Порядком или показателем числа a по модулю m называется такое наименьшее натуральное число a, что
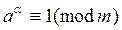 . (1)
. (1)
Обозначаем порядок числа a по модулю m через Pm (a). Порядок по модулю обладает следующими свойствами.
10 Если (a, m) =1 то Pm (a) существует и Pm (a) £. j(a).
20 Если (a, m) =1 и b º a (mod m), то Pm (b) = Pm (a).
30 Если d = Pm (a) и 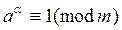 , то d|a.
, то d|a.
40 Если d = Pm (a), то d|j(m).
50 Если (a, m) =1 и d = Pm (a), 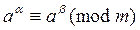 , то aºb(mod d).
, то aºb(mod d).
60 Если (a, m) =1 и d = Pm (a), то все степени 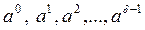 попарно несравнимы по модулю m..
попарно несравнимы по модулю m..
Алгоритм нахождения показателя r = Pm (a).
Ввод: Проверяемое число a и модуль m..
m:=0; r:= b;a 1:= a;;b 1:= b;
d:= function НОД (a, m);
if d >1 then s $:= «показатель Pm (a) не существует»
else P:=1; (q, r): = div (a, m);
while r ¹ 1 do P:= P + 1; (q, r): = div (ra, m); end while;
s $:= «показатель Pm (a) равен»;
end if
Вывод: s $и P.
Так как по свойству 40 порядок числа Pm (a) делит число j(m), то найдя каноническое разложение числа j(m) можно перебирать только делители числа j(m). Тогда алгоритм вычисления показателя принимает следующий вид.
Алгоритм нахождения показателя r = Pm (a).
Ввод: Проверяемое число a и модуль m..
m:=0; r:= b;a 1:= a;;b 1:= b;
d:= function НОД (a, m);
if d >1 then s $:= «показатель Pm (a) не существует»
else
f: = function j(m)
procedure Факторизация(f; A, k);{A- матрица, имеющая две строки, в первой строка матрицы, простые числа, делящие число m, вторая – соответствующие показатели этих простых чисел в каноническом разложении числа f, k – число различных простых множителей в каноническом разложении числа f }
d:=1; (q, r): = div (a, m);
for i:= 1 to k; B (i, 1):=1; B (i, 2):=0; end for; i:=1;
while r ¹ 1 do d:= d + 1; (q, r): = div (ra, m);
r:=0; {Перебор делителей числа j(m) до тех пор пока не будет r = 1}
while r = 0 do
if B (i, 2) < A (i, 2) then
B (i, 2):= B (i, 2) +1; p:= A (i, 2); v:= a;
while p > 0 do
(p, u):= div (p,2)
if u = 1 then (q, B (i, 1)):= div (B (i, 1)* v, m); end if
( q, v):= div (v* v, m);
end while;
r:= B (i, 1);
while i > 1 do i:=i- 1; B (i, 1):= r; B (i, 2):=0; end while;
else
i:=i+ 1;
end while;
end while;
P:=1;
for i:= 1 to k;
while B (i, 2)> 0 do P:= P*A (i, 1); B (i, 2):= B (i, 2)-1; end while;
end for;
s $:= «показатель Pm (a) равен»; P;
end if.
Вывод: s $и r.
Пример 2. Найти показатель числа 7 по модулю 15. Так как (7, 15) =1, то показатель существует. Вычисляем j(15) = 2×4 = 8. Делители числа j(15);1, 2, 4, 8.
Так как 7T1(mod 15), 72 º 49 º 4 T1(mod 15), 74 º 42 º1(mod 15), то P 15(7) = 4.



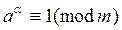 . (1)
. (1)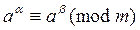 , то aºb(mod d).
, то aºb(mod d).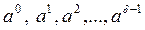 попарно несравнимы по модулю m..
попарно несравнимы по модулю m..


