Пусть g – первообразный корень по модулю m (m = p a или m = 2 p a, p – простое нечетное число), c = j(m). Тогда множество чисел
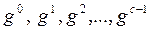 (1)
(1)
образует приведенную систему вычетов по модулю m. Поэтому для любого числа a взаимно простого с числом существует число gi из множества (1) сравнимое с ним по модулю m: т.е.
 . (2)
. (2)
Определение 1. Пусть g – первообразный корень по модулю m, (a, m) =1. Индексом числа a по модулю m и по основанию g называется такое целое число  , что
, что
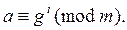
Обозначается индекс символом ind g a или короче, когда ясно, о каком основании идет речь.
Теорема 1. Для любого целого числа a взаимно простого с m по любому модуля m = p a или m = 2 p a, где p – простое нечетное число, индекс ind g a существует, и для любых целых чисел a, b взаимно простых с m выполняются свойства:
10 a º b (mod m) тогда и только тогда, когда ind g a º ind g b (mod j(m));
20 ind g (ab)º ind g a + ind g b (mod j(m));
30 если b | a, то ind g (a/b)º ind g a - ind g b (mod j(m));
40 если n Î N, то ind g an º n ×ind g a (mod j(m)).
Доказательство. Доказательство существования индекса следует из рассуждений в начале параграфа. Первое свойство следует из свойства первообразного корня.
Докажем свойство 30. Пусть ind g (ab) = i, ind g a = j, ind g b = k. Тогда по определению индекса имеем:

Отсюда
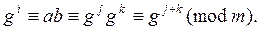
Тогда по свойству первообразного корня i º j + k (mod j(m)).
Свойства 30 и 40 доказываются аналогично.ÿ
В силу свойств 10-30 индекса числа a по основанию g и по модулю m называют иногда дискретным логарифмом числа a. Задача вычисления дискретного логарифма трудная задача. Одним из методов вычисления дискретного логарифма ind g a является метод перебора:
Чтобы найти ind g a необходимо начиная, например с n = 0, сравнивать элемент a с элементом gn по mod m: если a º gn (mod m), то ind g a = n, в противном случае находим gn +1 º gn g (mod m) и опять сравниваем элемент a с элементом gn + 1 и т.д. Если модуль m большой, то количество операций умножения, необходимое для вычисления дискретного логарифма велико.
Существует алгоритм, позволяющий существенно уменьшить время вычисления дискретного логарифма.
Теорема 2. Пусть t, r - натуральные числа, r 2 ³ t. Для любого целого числа l можно указать такие целые числа x и y, что
l º xr+y (mod t); 0£ x < r, 0 £ y < r. (3)
Доказательство. Можно предполагать, что 0£ l < t. Полагаем
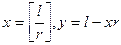 .
.
Имеем
 .
.
С другой стороны,
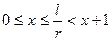 ,
,
поэтому
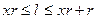
или
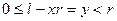 .ÿ
.ÿ
Теорема 2. Пусть g – первообразный корень по модулю m (m = p a или m = 2 p a, p – простое нечетное число), c = j(m). Тогда ind g a можно найти, выполнив не более 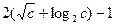 операций умножения по mod m.
операций умножения по mod m.
Доказательство. Пусть 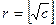 +1. Рассмотрим ряды вычетов
+1. Рассмотрим ряды вычетов
 (4)
(4)
 (5)
(5)
Если сравнение 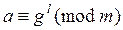 разрешимо относительно l, то по теореме 2 l представимо в виде (3). Тогда
разрешимо относительно l, то по теореме 2 l представимо в виде (3). Тогда
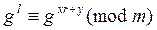
имеет место тогда и только тогда, когда
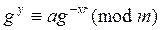 , (6)
, (6)
т.е. когда найдется элемент ряда (4), который сравним с каким-нибудь элементом ряда (5).
Сосчитаем число операций, позволяющих установить равенство (6). Для вычисления ряда (4) необходимо выполнить не более r -2 умножения по mod m. Для вычисления 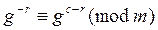 требуется выполнить не более
требуется выполнить не более 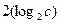 умножения по mod m и не более r -1 умножений для вычисления всех членов ряда (5). Поэтому число операций умножения для решения сравнения (6) не более
умножения по mod m и не более r -1 умножений для вычисления всех членов ряда (5). Поэтому число операций умножения для решения сравнения (6) не более
 . ÿ
. ÿ
Справедлива следующая теорема.
Теорема 4. Пусть g – первообразный корень по модулю m (m = p a или m = 2 p a, p – простое нечетное число), c = j(m) = r 1× r 2 ×…× rk,1< r 1< c,…, 1< rk < c. Тогда ind g a можно найти, выполнив не более
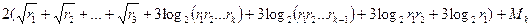
операций умножения по mod m, где  .
.
Для маленьких модулей составляются таблицы индексов.
Пример 1. Составить таблицу индексов по mod 19.
Первообразный корень по модулю 19 равен 2 (см. пример 2 параграфа 2). Вычисляем по модулю 19:
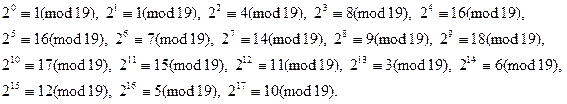
Таблица индексов по mod 19 имеет вид:
| a
| 0
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
|
| 0
| -
| 0
| 1
| 13
| 2
| 16
| 14
| 6
| 3
| 8
|
| 1
| 17
| 12
| 15
| 5
| 7
| 11
| 4
| 9
| 10
| -
|
Пример 2. Вычислить ind g 234, ind g -100 индексов по mod 19.
Так как 234 º 6(mod 19), то ind g 234º14(mod 18).
Так как -100 º 14(mod 19), то ind g -100º7(mod 18).
Пример 3. Найти x, y если по mod 19 ind g x = 24, ind g y = 39.
Так как ind g x = 24 º6(mod 18), то x º 7(mod 19).
Так как ind g y = 39 º3(mod 18), то y º 8(mod 19).
Теорема 5. Пусть m = p a или m = 2 p a, p – простое нечетное число, c = j(m), НОД(m, c) = d. Тогда сравнение
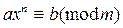 (7)
(7)
разрешимо тогда и только тогда, когда d | (ind g b - ind g a), при этом в случае его разрешимости оно имеет d решений по mod m.
Доказательство. По теореме 1 сравнение (7) равносильно сравнению
n × ind g x × º ind g b - ind g a (mod c) (8)
Последнее сравнение (8) линейное относительно ind g x. Оно разрешимо тогда и только тогда, когда d делит (ind g b - ind g a). При этом в случае разрешимости сравнение (8) имеет d решений по mod с:
ind g x º y 1(mod с),…, ind g x º yd (mod с),
которые дают d решений сравнения (7) по mod m:
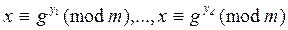 .ÿ
.ÿ
Пример 4. Решить сравнение 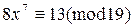 . Перейдем к индексам и получим:
. Перейдем к индексам и получим:
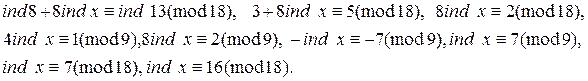
Тогда по таблице индексов находим x º 14(mod 19), то x º 5(mod 19).
Определение 2. Пусть (a, m) = 1. Число a называется вычетом n -й степени по mod m, если сравнение
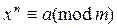 (9)
(9)
разрешимо.
Теорема 6. Пусть (a, m) = 1. Число a является вычетом n -й степени по mod m, тогда и только тогда, когда d |ind g a. В приведенной системе вычетов по по mod m имеется ровно с/ d вычетов n -й степени по mod m.
Доказательство. Первая часть теоремы следует из теоремы 5.
По свойству индекса, если a пробегает приведенную систему вычетов по mod m, то ind g a пробегают по mod с все числа множества 0, 1,…, с -1. Среди чисел последнего множества имеется с/ d чисел кратных d. Поэтому сравнение
n × ind g x × º ind g a (mod c),
а поэтому и сравнение (9) разрешимо для с/ d чисел a из приведенной системы вычетов по mod m. ÿ
Теорема 7. Пусть (a, m) = 1. Число a является вычетом n -й степени по mod m тогда и только тогда, когда
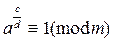 . (10)
. (10)
Доказательство. Разрешимость сравнения (9) равносильна условию
 .
.
Последнее сравнение равносильно условию
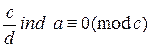 .
.
Последнее по свойству индекса равносильно условию (10).ÿ
Пример 5. Так как 3 делит ind 7=6 по mod 19, то число 7 является вычетом 3-й степени по mod 19. В приведенной системе вычетов по mod 19 имеется 18/3 = 6 вычетов 3-й степени: 1, 7, 8, 11, 12, 17.



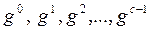 (1)
(1) . (2)
. (2)  , что
, что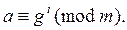

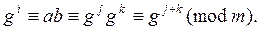
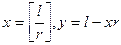 .
. .
.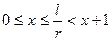 ,
,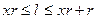
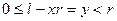 .ÿ
.ÿ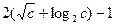 операций умножения по mod m.
операций умножения по mod m. 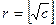 +1. Рассмотрим ряды вычетов
+1. Рассмотрим ряды вычетов (4)
(4) (5)
(5)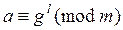 разрешимо относительно l, то по теореме 2 l представимо в виде (3). Тогда
разрешимо относительно l, то по теореме 2 l представимо в виде (3). Тогда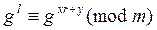
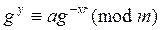 , (6)
, (6)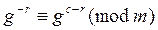 требуется выполнить не более
требуется выполнить не более 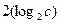 умножения по mod m и не более r -1 умножений для вычисления всех членов ряда (5). Поэтому число операций умножения для решения сравнения (6) не более
умножения по mod m и не более r -1 умножений для вычисления всех членов ряда (5). Поэтому число операций умножения для решения сравнения (6) не более . ÿ
. ÿ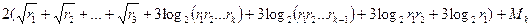
 .
.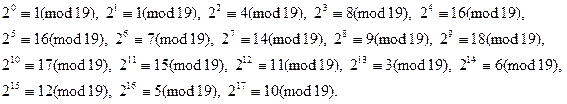
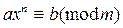 (7)
(7)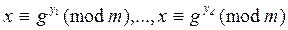 .ÿ
.ÿ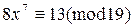 . Перейдем к индексам и получим:
. Перейдем к индексам и получим: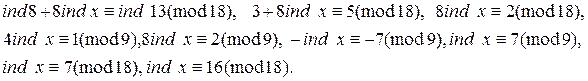
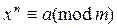 (9)
(9)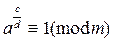 . (10)
. (10) .
.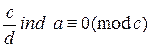 .
.


