Тема: Графы и сети
Моделирование на графах
План лекции:
1. Основные понятия теории графов.
2. Способы задания графов.
3. Маршруты в графе.
4. Взвешенные графы.
5. Понятие сети.
6. Применение теории графов к моделированию систем.
7. Планирование и управление в сетях.
8. Оптимальный путь. Алгоритм Дейкстры. Алгоритм Беллмана–Мура.
9. Критический путь. Алгоритм Беллмана–Калаба.
Основные понятия теории графов
Граф – совокупность точек, соедененных определенным образом. Предметом рассмотрения теории графов является множество элементов, между которыми существуют связи.
В виде графов можно представить сеть железных дорог, сеть телефонных связей, сеть трубопроводов, информационную систему, структуру управления сложной иерархической системой и т.д.
Таким образом, во многих случаях, не вдаваясь в физический смысл, можно изобразить некоторые черты объекта в виде схемы, которая отображает внутренние связи и не зависит от природы объекта. Такие схемы называют графами.
Определение.Графом (конечным графом)  называется совокупность двух множеств – конечного множества
называется совокупность двух множеств – конечного множества  и множества
и множества  пар элементов из
пар элементов из  . Элементы множества
. Элементы множества  называются вершинами графа, а элементы множества
называются вершинами графа, а элементы множества  – его ребрами.
– его ребрами.
Если элементами множества  являются упорядоченные пары, то граф
являются упорядоченные пары, то граф 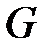 называется ориентированным (или орграфом). В этом случае элементы множества
называется ориентированным (или орграфом). В этом случае элементы множества  называются узлами, а элементы множества
называются узлами, а элементы множества 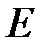 – дугами. В ориентированном графе первая по порядку вершина называется его началом, другая – его концом. Орграф обозначают
– дугами. В ориентированном графе первая по порядку вершина называется его началом, другая – его концом. Орграф обозначают  .
.
Если элементом множества  является пара одинаковых элементов множества
является пара одинаковых элементов множества  , то такой элемент множества
, то такой элемент множества 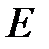 называется петлей, а граф
называется петлей, а граф  называется графом с петлями.
называется графом с петлями.
Если  является не множеством, а набором, который содержит несколько одинаковых элементов, то эти элементы называются кратными ребрами.
является не множеством, а набором, который содержит несколько одинаковых элементов, то эти элементы называются кратными ребрами.
Пример 1. Пусть задано множество  и
и
 .
.
Тогда множества  и
и  определяют граф (мультиграф)
определяют граф (мультиграф)  ,
,
 – петля,
– петля,  – кратное ребро.
– кратное ребро.
Пример 2. Пусть задано множество  и
и
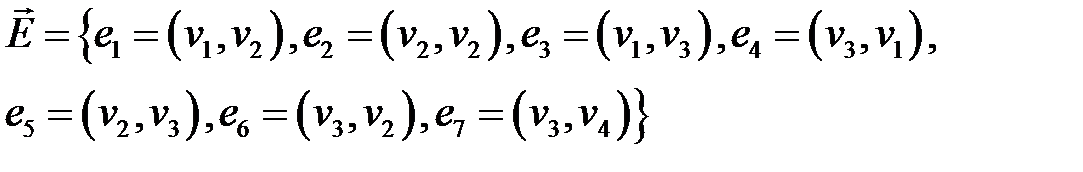 .
.
Тогда множества  и
и  определяют орграф
определяют орграф  .
.
Любой граф  определяется отношением инцидентности между множествами вершин
определяется отношением инцидентности между множествами вершин  и ребер
и ребер  . Если вершина
. Если вершина  является концом ребра
является концом ребра 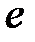 , то говорят, что
, то говорят, что  инцидентна
инцидентна  . Отношение инцидентности является обобщением отношения принадлежности, оно нерефлексивно и симметрично. Заметим, что каждый элемент
. Отношение инцидентности является обобщением отношения принадлежности, оно нерефлексивно и симметрично. Заметим, что каждый элемент  инцидентный точно двум элементам
инцидентный точно двум элементам 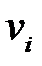 и
и  из
из  .
.
Определение. Число ребер, инцидентных вершине  , называется степенью вершины
, называется степенью вершины  и обозначается
и обозначается  .
.
 .
.
В орграфе число дуг, выходящих из узла  , называется полустепенью выхода (обозначается
, называется полустепенью выхода (обозначается  ), и входящих – полустепенью входа (обозначается
), и входящих – полустепенью входа (обозначается  ).
).
2. Способы задания графов
Граф 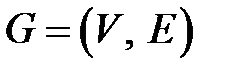 считается заданным, если определены множества его вершин
считается заданным, если определены множества его вершин  и ребер
и ребер  , а также отношение инцидентности между ними.
, а также отношение инцидентности между ними.
Граф может быть задан:
1) Геометрическим способом
Геометрическим изображением графа  называется фигура
называется фигура  в евклидовом пространстве, если между вершинами фигуры
в евклидовом пространстве, если между вершинами фигуры  и вершинами графа
и вершинами графа  , а также между кривыми фигуры
, а также между кривыми фигуры  и ребрами графа
и ребрами графа 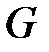 существует взаимно однозначное соответствие (соответствующие кривые и ребра соединяют соответствующие вершины).
существует взаимно однозначное соответствие (соответствующие кривые и ребра соединяют соответствующие вершины).
При изображении орграфов направления ребер изображаются стрелками, которые примыкают к их концам. Орграф может иметь петли, кратные ребра, а также ребра, которые соединяют одни и те же вершины, но идут в противоположных направлениях (примеры 1,2).
Пример 1. Пример 2.
2) Алгебраическим способом, для которого используются матрицы смежности и матрицы инцидентности.
Определение.Матрицей смежности графа  называется квадратная
называется квадратная  – матрица
– матрица  , где
, где

Столбцам и строкам матрицы смежности соответствуют вершины графа. Для неориентированного графа  – число ребер, инцидентных
– число ребер, инцидентных  -й и
-й и  -й вершинам. Для ориентированного графа
-й вершинам. Для ориентированного графа  – число ребер с началом в
– число ребер с началом в  -й и концом в
-й и концом в 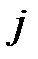 -й вершине.
-й вершине.
Свойства матрицы смежности:
1. Матрица смежности неориентированного графа симметрична ( ), а ориентированного – не обязательно.
), а ориентированного – не обязательно.
2. Сумма элементов  -й строки или
-й строки или  -го столбца матрицы смежности неориентированного графа равна степени
-го столбца матрицы смежности неориентированного графа равна степени 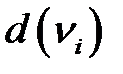 вершины
вершины  .
.
3. Сумма элементов верхнего правого треугольника, расположенного над главной диагональю матрицы смежности неориентированного графа, включая последнюю, равна количеству ребер графа.
4. Сумма элементов 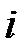 -й строки матрицы смежности ориентированного графа равна полустепени выхода
-й строки матрицы смежности ориентированного графа равна полустепени выхода  узла
узла  .
.
5. Сумма элементов  -го столбца матрицы смежности ориентированного графа равна полустепени
-го столбца матрицы смежности ориентированного графа равна полустепени 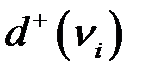 входа узла
входа узла  .
.
6. Сумма всех элементов матрицы смежности ориентированного графа равна количеству его дуг.
Матрицы смежности графов из примеров 1 и 2:


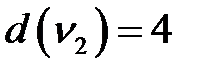 ,
,  ,
, 
Определение.Матрицей инцидентности графа  называется
называется  – матрица
– матрица  , где
, где

Определение. Матрицей инцидентности орграфа  называется
называется  – матрица
– матрица  , где
, где

Свойства матрицы инцидентности:
1. В каждой строке матрицы инцидентности неориентированного или ориентированного графа только два элемента не равны 0 (или один, если ребро является петлей). (Поэтому такой способ задания недостаточно экономный.)
2. Сумма элементов  -й строки матрицы инцидентности ориентированного графа равна 0.
-й строки матрицы инцидентности ориентированного графа равна 0.
Матрицы инцидентности графов из примеров 1 и 2


Определение. Графы  и
и 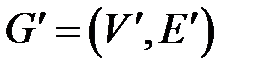 называются изоморфными, если существует взаимно однозначное соответствие между множествами их вершин и множествами их ребер, которое сохраняет отношение инцидентности (соответствующие ребра соединяют соответствующие вершины).
называются изоморфными, если существует взаимно однозначное соответствие между множествами их вершин и множествами их ребер, которое сохраняет отношение инцидентности (соответствующие ребра соединяют соответствующие вершины).
Изоморфизм графов является отношением эквивалентности, т.е. имеет свойства рефлексивности, симметричности, транзитивности..
Маршруты в графе
Определение. Маршрутом 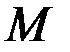 в графе
в графе  называется такая последовательность чередующихся вершин и ребер
называется такая последовательность чередующихся вершин и ребер  , в которой любые два соседних элемента инцидентны. В ориентированном графе
, в которой любые два соседних элемента инцидентны. В ориентированном графе  – начало ребра
– начало ребра  ,
, 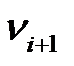 – конец ребра
– конец ребра 
Очевидно, маршрут 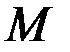 в графе
в графе  можно задать как последовательностью вершин, так и последовательностью ребер.
можно задать как последовательностью вершин, так и последовательностью ребер.
Определение. Вершина  называется началом маршрута, вершина
называется началом маршрута, вершина  называется концом маршрута. Вершины, инцидентные ребрам маршрута, кроме начальной и конечной, называются внутренними или промежуточными.
называется концом маршрута. Вершины, инцидентные ребрам маршрута, кроме начальной и конечной, называются внутренними или промежуточными.
Если начало и конец маршрута совпадают:  , то маршрут
, то маршрут  называется замкнутым. В противном случае маршрут называется открытым.
называется замкнутым. В противном случае маршрут называется открытым.
Определение. Маршрут  называется цепью, если все его ребра разные. Маршрут называется простой цепью, если все его вершины разные.
называется цепью, если все его ребра разные. Маршрут называется простой цепью, если все его вершины разные.
Определение. Замкнутая цепь называется циклом. Замкнутая простая цепь называется простым циклом. Граф без циклов называют ацикличным.
Для орграфов цепь называется путём, а цикл – контуром.
Цепь (путь) является элементарной, если среди её вершин нет одинаковых.
Определение. Длиной маршрута (цепи, простой цепи) называется число ребер в порядке их прохождения.
Маршрут, состоящий из одной вершины, имеет нулевую длину.
Определение. Минимальная длина простой цепи с началом 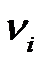 и концом
и концом  называется расстоянием
называется расстоянием  между этими вершинами.
между этими вершинами.
Маршруты в графах из примеров 1 и 2
Пример 1.
 – маршрут из вершины
– маршрут из вершины  до вершины
до вершины 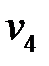 длины 2 – простая цепь;
длины 2 – простая цепь;
 – простой цикл,
– простой цикл,
Расстояние  между вершиной
между вершиной  и вершиной
и вершиной 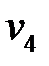 равно 2.
равно 2.
Пример 2.
 – простой путь из вершины
– простой путь из вершины  до вершины
до вершины  , длина 2.
, длина 2.
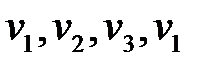 – простой контур длины 3.
– простой контур длины 3.
Определение. Граф называется связным, если между любой парой его вершин существует хотя бы одна цепь.
Орграф называется сильно связным, если между любой парой его вершин существует хотя бы один путь.
Граф без петель, в котором любые две вершины могут быть соединены одной элементарной цепью, называется деревом.
Дерево не содержит элементарных циклов. Удаление любой дуги приводит к распаду дерева на несвязные части, каждая из которых будет деревом. Число дуг любого дерева на единицу меньше числа его вершин.
Если в дереве  выделена какая-либо вершина
выделена какая-либо вершина 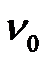 , то эту вершину называют корнем дерева
, то эту вершину называют корнем дерева 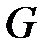 , а само дерево называют деревом с корнем.
, а само дерево называют деревом с корнем.
Взвешенные графы
Определение. Граф 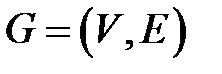 называется взвешенным, если каждому ребру
называется взвешенным, если каждому ребру  поставлено в соответствие некоторое число
поставлено в соответствие некоторое число  , которое называется его длиной (или весом, или стоимостью).
, которое называется его длиной (или весом, или стоимостью).
Орграф  называется взвешенным, если каждой дуге
называется взвешенным, если каждой дуге  поставлено в соответствие некоторое число
поставлено в соответствие некоторое число  , которое называется её длиной (или весом, или стоимостью).
, которое называется её длиной (или весом, или стоимостью).
Алгебраично взвешенный граф задаётся с помощью матрицы длин ребер.
Определение. Матрицей длин ребер или матрицей весов графа  называется матрица
называется матрица  , где
, где 
Матрицей длин дуг или матрицей весов орграфа  называется матрица
называется матрица  , где
, где 
Свойства матрицы длин ребер (дуг)
1. Матрица длин ребернеориентированного графа симметрична (т.е.  )
)
2. Матрица длин дуг орграфа не обязательно симметрична.
Пример. Для взвешенного графа, изображенного на рисунке, матрица  имеет вид:
имеет вид:

Для взвешенного орграфа, зображеного на рисунке, матрица 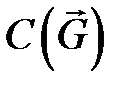 имеет вид:
имеет вид:

Понятие сети
Обобщением понятия графа является понятие сети.
Определение. Совокупность множества  и множества
и множества  , в которой каждое
, в которой каждое 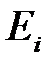 является набором элементов из
является набором элементов из  , т.е.
, т.е.  , называется сетью и обозначается
, называется сетью и обозначается  . Элементы множества
. Элементы множества  называются вершинами, а элементы из набора
называются вершинами, а элементы из набора 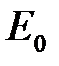 – полюсами сети.
– полюсами сети.
Пример. V = (1, 2, 3, 4, 5, 6, 7), E = (E0, E1, E2, E3, E4, E5), де Е0 = (1, 2, 6); Е1 = (1, 3, 3, 4, 5), Е2 = (4, 4, 4, 5, 6), Е3 = Е4 = (2, 4), Е5 = (2, 5, 6, 7).
Тогда  будет сетью.
будет сетью.
Таким образом, сеть – это граф с выделенным множеством вершин Е0.
Определение. Если 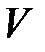 и Е – конечные множества, то сеть называется конечной.
и Е – конечные множества, то сеть называется конечной.
Подобно тому, как это было сделано в случае графов, можно получить графическое изображение сети. Пусть  – сеть. Разобьём множество
– сеть. Разобьём множество  на 3 части, которые между собой не пересекаются:
на 3 части, которые между собой не пересекаются:  – множество полюсов;
– множество полюсов; 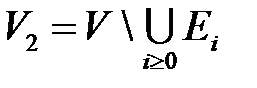 – множество изолированных вершин, отличных от полюсов;
– множество изолированных вершин, отличных от полюсов;  – остальные вершины. Каждой вершине поставим в трехмерном евклидовом пространстве точку. Каждому набору
– остальные вершины. Каждой вершине поставим в трехмерном евклидовом пространстве точку. Каждому набору 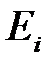 из
из  ,
,  , поставим круг (или прямоугольник), на границе которого выбраны попарно разные вершины из набора
, поставим круг (или прямоугольник), на границе которого выбраны попарно разные вершины из набора  . При этом необходимо, чтобы круги не пересекались и не содержали ранее выбранных вершин. Потом все точки, соответствующие одной и той же вершине
. При этом необходимо, чтобы круги не пересекались и не содержали ранее выбранных вершин. Потом все точки, соответствующие одной и той же вершине  , соединяются. Полученная в результате геометрическая фигура называется геометрическим изображением сети
, соединяются. Полученная в результате геометрическая фигура называется геометрическим изображением сети  .
.
Пример. Данная фигура является геометрическим изображением сети из предыдущего примера.
Рис.3
Рассмотрим некоторые классы сетей.
1) Класс сетей, у которых  и каждый набор
и каждый набор  ,
,  , состоит из 2-х элементов множества
, состоит из 2-х элементов множества  , совпадает с классом графов.
, совпадает с классом графов.
2) Дерево с корнем является однополюсной сетью, т.е.  .
.
Планирование и управление в сетях
Проектом (комплексом операций) называют совокупность операций, необходимых для достяжения некоторой цели, время выполнения каждой из которых известно и которые связаны отношением порядка.
Каждая отдельная работа, входящая в комплекс (проект), требует затрат определенного времени. Некоторые операции могут выполняться только в определенном порядке. Нельзя, например, закладывать фундамент, если еще не выкопали котлован для него. Существуют работы, входящие в комплекс, которые могут выполняться независимо друг от друга, одновременно. Например, одновременно можно проводить работы по изготовлению декораций и работа над ролями.
При выполнении комплекса работ всегда можно выделить ряд событий, т.е. итогов некоторой деятельности, что позволяет приступить к выполнению следующей работы. Примеры событий: котлован выкопан, роли распределены, декорации изготовлены.
Если каждому событию поставить в соответствие вершину графа, а каждой работе – ориентированное ребро, то получим некоторый граф. Он будет отображать последовательность выполнения отдельных работ и наступление событий в едином комплексе. Если над работами поставить время, необходимое для завершения соответствующей работы, тогда получим сеть.
Таким образом, проект (комплекс операций) может быть представлен сетью, которая называется «моделью проекта в виде сети» или логической диаграммой, дуги которой являются операциями. Изображение такой сети называется графиком сети.
Пример:
Рис.4
При построении сети необходимо для каждой операции знать операции, которые предшествуют данной. Сеть отображает таким образом соотношения порядка, которые существуют во множестве операций.
Тема: Графы и сети
Моделирование на графах
План лекции:
1. Основные понятия теории графов.
2. Способы задания графов.
3. Маршруты в графе.
4. Взвешенные графы.
5. Понятие сети.
6. Применение теории графов к моделированию систем.
7. Планирование и управление в сетях.
8. Оптимальный путь. Алгоритм Дейкстры. Алгоритм Беллмана–Мура.
9. Критический путь. Алгоритм Беллмана–Калаба.
Основные понятия теории графов
Граф – совокупность точек, соедененных определенным образом. Предметом рассмотрения теории графов является множество элементов, между которыми существуют связи.
В виде графов можно представить сеть железных дорог, сеть телефонных связей, сеть трубопроводов, информационную систему, структуру управления сложной иерархической системой и т.д.
Таким образом, во многих случаях, не вдаваясь в физический смысл, можно изобразить некоторые черты объекта в виде схемы, которая отображает внутренние связи и не зависит от природы объекта. Такие схемы называют графами.
Определение.Графом (конечным графом)  называется совокупность двух множеств – конечного множества
называется совокупность двух множеств – конечного множества  и множества
и множества  пар элементов из
пар элементов из  . Элементы множества
. Элементы множества  называются вершинами графа, а элементы множества
называются вершинами графа, а элементы множества  – его ребрами.
– его ребрами.
Если элементами множества  являются упорядоченные пары, то граф
являются упорядоченные пары, то граф 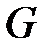 называется ориентированным (или орграфом). В этом случае элементы множества
называется ориентированным (или орграфом). В этом случае элементы множества  называются узлами, а элементы множества
называются узлами, а элементы множества 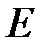 – дугами. В ориентированном графе первая по порядку вершина называется его началом, другая – его концом. Орграф обозначают
– дугами. В ориентированном графе первая по порядку вершина называется его началом, другая – его концом. Орграф обозначают  .
.
Если элементом множества  является пара одинаковых элементов множества
является пара одинаковых элементов множества  , то такой элемент множества
, то такой элемент множества 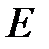 называется петлей, а граф
называется петлей, а граф  называется графом с петлями.
называется графом с петлями.
Если  является не множеством, а набором, который содержит несколько одинаковых элементов, то эти элементы называются кратными ребрами.
является не множеством, а набором, который содержит несколько одинаковых элементов, то эти элементы называются кратными ребрами.
Пример 1. Пусть задано множество  и
и
 .
.
Тогда множества  и
и  определяют граф (мультиграф)
определяют граф (мультиграф)  ,
,
 – петля,
– петля,  – кратное ребро.
– кратное ребро.
Пример 2. Пусть задано множество  и
и
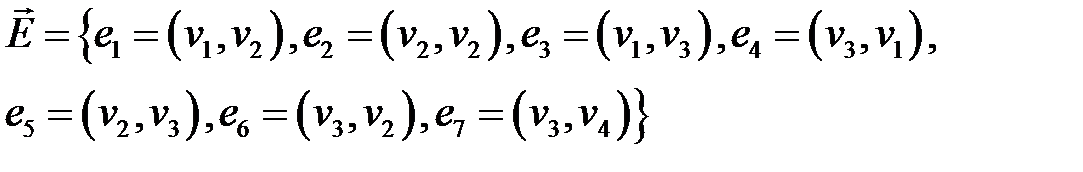 .
.
Тогда множества  и
и  определяют орграф
определяют орграф  .
.
Любой граф  определяется отношением инцидентности между множествами вершин
определяется отношением инцидентности между множествами вершин  и ребер
и ребер  . Если вершина
. Если вершина  является концом ребра
является концом ребра 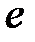 , то говорят, что
, то говорят, что  инцидентна
инцидентна  . Отношение инцидентности является обобщением отношения принадлежности, оно нерефлексивно и симметрично. Заметим, что каждый элемент
. Отношение инцидентности является обобщением отношения принадлежности, оно нерефлексивно и симметрично. Заметим, что каждый элемент  инцидентный точно двум элементам
инцидентный точно двум элементам 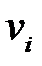 и
и  из
из  .
.
Определение. Число ребер, инцидентных вершине  , называется степенью вершины
, называется степенью вершины  и обозначается
и обозначается  .
.
 .
.
В орграфе число дуг, выходящих из узла  , называется полустепенью выхода (обозначается
, называется полустепенью выхода (обозначается  ), и входящих – полустепенью входа (обозначается
), и входящих – полустепенью входа (обозначается  ).
).
2. Способы задания графов
Граф 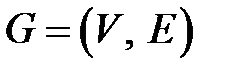 считается заданным, если определены множества его вершин
считается заданным, если определены множества его вершин  и ребер
и ребер  , а также отношение инцидентности между ними.
, а также отношение инцидентности между ними.
Граф может быть задан:
1) Геометрическим способом
Геометрическим изображением графа  называется фигура
называется фигура  в евклидовом пространстве, если между вершинами фигуры
в евклидовом пространстве, если между вершинами фигуры  и вершинами графа
и вершинами графа  , а также между кривыми фигуры
, а также между кривыми фигуры  и ребрами графа
и ребрами графа 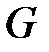 существует взаимно однозначное соответствие (соответствующие кривые и ребра соединяют соответствующие вершины).
существует взаимно однозначное соответствие (соответствующие кривые и ребра соединяют соответствующие вершины).
При изображении орграфов направления ребер изображаются стрелками, которые примыкают к их концам. Орграф может иметь петли, кратные ребра, а также ребра, которые соединяют одни и те же вершины, но идут в противоположных направлениях (примеры 1,2).
Пример 1. Пример 2.



 называется совокупность двух множеств – конечного множества
называется совокупность двух множеств – конечного множества  и множества
и множества  пар элементов из
пар элементов из  . Элементы множества
. Элементы множества  называются вершинами графа, а элементы множества
называются вершинами графа, а элементы множества  – его ребрами.
– его ребрами. являются упорядоченные пары, то граф
являются упорядоченные пары, то граф 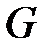 называется ориентированным (или орграфом). В этом случае элементы множества
называется ориентированным (или орграфом). В этом случае элементы множества  называются узлами, а элементы множества
называются узлами, а элементы множества 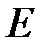 – дугами. В ориентированном графе первая по порядку вершина называется его началом, другая – его концом. Орграф обозначают
– дугами. В ориентированном графе первая по порядку вершина называется его началом, другая – его концом. Орграф обозначают  .
. является пара одинаковых элементов множества
является пара одинаковых элементов множества  , то такой элемент множества
, то такой элемент множества 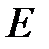 называется петлей, а граф
называется петлей, а граф  называется графом с петлями.
называется графом с петлями. является не множеством, а набором, который содержит несколько одинаковых элементов, то эти элементы называются кратными ребрами.
является не множеством, а набором, который содержит несколько одинаковых элементов, то эти элементы называются кратными ребрами. и
и .
. и
и  определяют граф (мультиграф)
определяют граф (мультиграф)  ,
, – петля,
– петля,  – кратное ребро.
– кратное ребро. и
и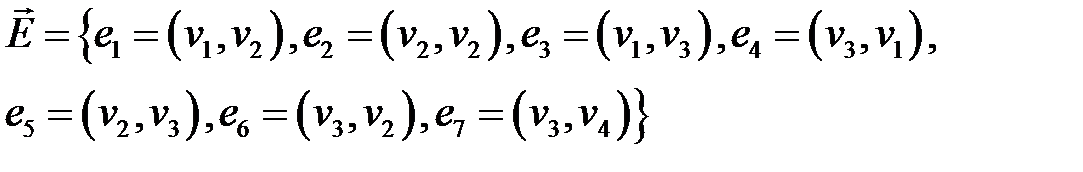 .
. и
и  определяют орграф
определяют орграф  .
. определяется отношением инцидентности между множествами вершин
определяется отношением инцидентности между множествами вершин  и ребер
и ребер  . Если вершина
. Если вершина  является концом ребра
является концом ребра 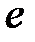 , то говорят, что
, то говорят, что  инцидентна
инцидентна  . Отношение инцидентности является обобщением отношения принадлежности, оно нерефлексивно и симметрично. Заметим, что каждый элемент
. Отношение инцидентности является обобщением отношения принадлежности, оно нерефлексивно и симметрично. Заметим, что каждый элемент  инцидентный точно двум элементам
инцидентный точно двум элементам 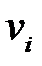 и
и  из
из  .
. , называется степенью вершины
, называется степенью вершины  и обозначается
и обозначается  .
. .
. , называется полустепенью выхода (обозначается
, называется полустепенью выхода (обозначается  ), и входящих – полустепенью входа (обозначается
), и входящих – полустепенью входа (обозначается  ).
).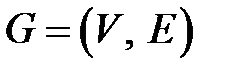 считается заданным, если определены множества его вершин
считается заданным, если определены множества его вершин  и ребер
и ребер  , а также отношение инцидентности между ними.
, а также отношение инцидентности между ними. называется фигура
называется фигура  в евклидовом пространстве, если между вершинами фигуры
в евклидовом пространстве, если между вершинами фигуры  и вершинами графа
и вершинами графа  , а также между кривыми фигуры
, а также между кривыми фигуры  и ребрами графа
и ребрами графа 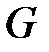 существует взаимно однозначное соответствие (соответствующие кривые и ребра соединяют соответствующие вершины).
существует взаимно однозначное соответствие (соответствующие кривые и ребра соединяют соответствующие вершины).












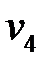


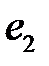

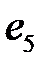



 называется квадратная
называется квадратная  – матрица
– матрица  , где
, где
 – число ребер, инцидентных
– число ребер, инцидентных  -й и
-й и  -й вершинам. Для ориентированного графа
-й вершинам. Для ориентированного графа  – число ребер с началом в
– число ребер с началом в  -й и концом в
-й и концом в 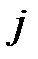 -й вершине.
-й вершине. ), а ориентированного – не обязательно.
), а ориентированного – не обязательно. -й строки или
-й строки или  -го столбца матрицы смежности неориентированного графа равна степени
-го столбца матрицы смежности неориентированного графа равна степени 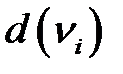 вершины
вершины  .
.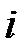 -й строки матрицы смежности ориентированного графа равна полустепени выхода
-й строки матрицы смежности ориентированного графа равна полустепени выхода  узла
узла  .
. -го столбца матрицы смежности ориентированного графа равна полустепени
-го столбца матрицы смежности ориентированного графа равна полустепени 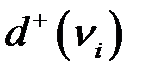 входа узла
входа узла  .
.

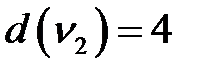 ,
,  ,
, 
 называется
называется  – матрица
– матрица  , где
, где
 называется
называется  – матрица
– матрица  , где
, где
 -й строки матрицы инцидентности ориентированного графа равна 0.
-й строки матрицы инцидентности ориентированного графа равна 0.

 и
и 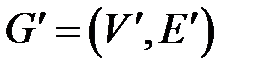 называются изоморфными, если существует взаимно однозначное соответствие между множествами их вершин и множествами их ребер, которое сохраняет отношение инцидентности (соответствующие ребра соединяют соответствующие вершины).
называются изоморфными, если существует взаимно однозначное соответствие между множествами их вершин и множествами их ребер, которое сохраняет отношение инцидентности (соответствующие ребра соединяют соответствующие вершины).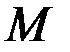 в графе
в графе  называется такая последовательность чередующихся вершин и ребер
называется такая последовательность чередующихся вершин и ребер  , в которой любые два соседних элемента инцидентны. В ориентированном графе
, в которой любые два соседних элемента инцидентны. В ориентированном графе  – начало ребра
– начало ребра  ,
, 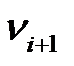 – конец ребра
– конец ребра 
 можно задать как последовательностью вершин, так и последовательностью ребер.
можно задать как последовательностью вершин, так и последовательностью ребер. называется началом маршрута, вершина
называется началом маршрута, вершина  называется концом маршрута. Вершины, инцидентные ребрам маршрута, кроме начальной и конечной, называются внутренними или промежуточными.
называется концом маршрута. Вершины, инцидентные ребрам маршрута, кроме начальной и конечной, называются внутренними или промежуточными. , то маршрут
, то маршрут  называется замкнутым. В противном случае маршрут называется открытым.
называется замкнутым. В противном случае маршрут называется открытым. называется цепью, если все его ребра разные. Маршрут называется простой цепью, если все его вершины разные.
называется цепью, если все его ребра разные. Маршрут называется простой цепью, если все его вершины разные.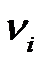 и концом
и концом  называется расстоянием
называется расстоянием  между этими вершинами.
между этими вершинами. – маршрут из вершины
– маршрут из вершины  до вершины
до вершины 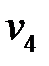 длины 2 – простая цепь;
длины 2 – простая цепь; – простой цикл,
– простой цикл, между вершиной
между вершиной  и вершиной
и вершиной 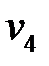 равно 2.
равно 2. – простой путь из вершины
– простой путь из вершины  до вершины
до вершины  , длина 2.
, длина 2.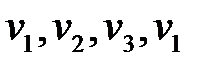 – простой контур длины 3.
– простой контур длины 3. выделена какая-либо вершина
выделена какая-либо вершина 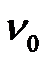 , то эту вершину называют корнем дерева
, то эту вершину называют корнем дерева 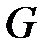 , а само дерево называют деревом с корнем.
, а само дерево называют деревом с корнем.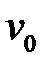
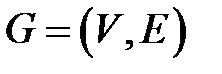 называется взвешенным, если каждому ребру
называется взвешенным, если каждому ребру  поставлено в соответствие некоторое число
поставлено в соответствие некоторое число  , которое называется его длиной (или весом, или стоимостью).
, которое называется его длиной (или весом, или стоимостью). называется взвешенным, если каждой дуге
называется взвешенным, если каждой дуге  поставлено в соответствие некоторое число
поставлено в соответствие некоторое число  , которое называется её длиной (или весом, или стоимостью).
, которое называется её длиной (или весом, или стоимостью). называется матрица
называется матрица  , где
, где 
 называется матрица
называется матрица  , где
, где 
 )
) имеет вид:
имеет вид:





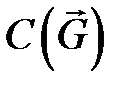 имеет вид:
имеет вид:

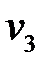



 и множества
и множества  , в которой каждое
, в которой каждое 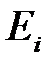 является набором элементов из
является набором элементов из  , т.е.
, т.е.  , называется сетью и обозначается
, называется сетью и обозначается  . Элементы множества
. Элементы множества  называются вершинами, а элементы из набора
называются вершинами, а элементы из набора 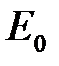 – полюсами сети.
– полюсами сети. будет сетью.
будет сетью.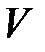 и Е – конечные множества, то сеть называется конечной.
и Е – конечные множества, то сеть называется конечной. – сеть. Разобьём множество
– сеть. Разобьём множество  на 3 части, которые между собой не пересекаются:
на 3 части, которые между собой не пересекаются:  – множество полюсов;
– множество полюсов; 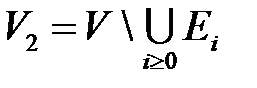 – множество изолированных вершин, отличных от полюсов;
– множество изолированных вершин, отличных от полюсов;  – остальные вершины. Каждой вершине поставим в трехмерном евклидовом пространстве точку. Каждому набору
– остальные вершины. Каждой вершине поставим в трехмерном евклидовом пространстве точку. Каждому набору 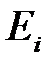 из
из  ,
,  , поставим круг (или прямоугольник), на границе которого выбраны попарно разные вершины из набора
, поставим круг (или прямоугольник), на границе которого выбраны попарно разные вершины из набора  . При этом необходимо, чтобы круги не пересекались и не содержали ранее выбранных вершин. Потом все точки, соответствующие одной и той же вершине
. При этом необходимо, чтобы круги не пересекались и не содержали ранее выбранных вершин. Потом все точки, соответствующие одной и той же вершине  , соединяются. Полученная в результате геометрическая фигура называется геометрическим изображением сети
, соединяются. Полученная в результате геометрическая фигура называется геометрическим изображением сети  .
.  и каждый набор
и каждый набор  ,
,  , состоит из 2-х элементов множества
, состоит из 2-х элементов множества  , совпадает с классом графов.
, совпадает с классом графов. .
.


