МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
СТАРООСКОЛЬСКИЙ ФИЛИАЛ
ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ
ВЫСШЕГО ОБРАЗОВАНИЯ
«РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГЕОЛОГОРАЗВЕДОЧНЫЙ УНИВЕРСИТЕТ
Имени СЕРГО ОРДЖОНИКИДЗЕ»
СОФ МГРИ
Г.Н.ЗУБКОВА
Н.С.ГАВРЮШКИНА
МАТЕМАТИКА
Методические указания для практических занятий и самостоятельной работы студентов 2 курса.
Старый Оскол
2018
Рецензент
СТИ НИТУ МИСиС , доцент, кандидат технических наук О.С. Кравцова
Краткая аннотация:
Методические указания являются частью основной профессиональной образовательной программы для студентов 2 курса всех специальностей в соответствии с требованиями ФГОС СПО.
Методические указания адресованы студентам очной формы обучения.
Целью данного пособия является помощь студентам выработать навыки решения практических задач по математике.
Оно включает в себя основной теоретический материал и образцы решения типовых задач.
Пособие будет полезно тем студентам, которые по различным причинам не смогли посетить все учебные занятия.
Также оно будет полезно для подготовки к практическим занятиям, для более успешного понимания и усвоения материала.
Издается по решению
ПЦК математики,физики и информатики
Протокол № от __ _ 2018 г.
Председатель ПЦК: ____ _______
Г.Н.Зубкова
Количество страниц:_______
Количество условных печатных листов:_______
Оглавление
1. Глава 1. Математический анализ………………………3
1.1. Предел функции……………………………………3
1.2. Производная функции……………………………..7
1.3. Производная сложной функции……………..…..10
1.4 Интегральное исчисление………………………...16
1.5 Неопределенный  . Его свойства………………17
. Его свойства………………17
1.6. Определенный интеграл. Вычисление
площадей плоских фигур……………………………..21
1.7. Метод замены переменной
(метод подстановки)………………………………22
1.8. Дифференциальные уравнения…………………..23
1.9. Однородные дифференциальные
уравнения первого порядка………………………..25
1.10 Частные производные…………………………….27
2. Глава 2. Ряды……………………………………………28
2.1. Числовые ряды……………………………………..28
2.2. Знакопеременные ряды…………………………...31
2.3. Функциональные ряды…………………………….31
3. Глава 3. Основы дискретной математики…………….33
3.1. Множества и отношения………………………….33
4. Глава 4. Основы теории комплексных чисел…………35
4.1. Алгебраическая форма комплексного числа…….35
4.2. Геометрическое представление
комплексных чисел…………………………………….37
4.3. Показательная форма комплексного числа………39
5. Глава 5. Основы теории вероятностей………………….42
5.1. Вероятность. Случайные события…………………42
5.2. Случайная величина. Ее функция распределения..44
5.3. Математическое ожидание и дисперсия
случайной величины………………………………..45
Самостоятельные работы ………………………………..48
Контрольная работа № 1………………………………...57
Глава 1. Математический анализ.
Предел функции.
1. Определение. Таблица замечательных пределов.
Обозначения:  множество вещественных чисел.
множество вещественных чисел.
Опр. 1.1.  , допустим, что каждому значению
, допустим, что каждому значению  по какому – либо закону поставлено в соответствие
по какому – либо закону поставлено в соответствие  . Это сопоставление определяет однозначное отображение и называется функцией одной переменной с областью определения X и множеством значений Y.
. Это сопоставление определяет однозначное отображение и называется функцией одной переменной с областью определения X и множеством значений Y.
Обозн. 
Пример.

Пусть  определена в некоторой окрестности точки а.
определена в некоторой окрестности точки а.
Опр. 1.2. число b называется пределом функции  при
при  , если для любой последовательности аргументов
, если для любой последовательности аргументов 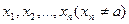 сходящихся к а, соответствующая последовательность значений функций
сходящихся к а, соответствующая последовательность значений функций  сходится у b.
сходится у b.
Обозн. 
Таблица пределов:

Свойства пределов:
1)  ;
;
2)  ;
;
3)  ;
;
4) 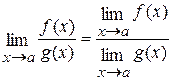 (при
(при  ).
).
Пример. Вычислить предел.

Задача:

1.2. Производная функции.
1. Непрерывность функции.
Опр. 2.1. Функция  называется непрерывной в точке а, если она имеет предел
называется непрерывной в точке а, если она имеет предел  и этот предел равен значению функции в этой точке, т.е.
и этот предел равен значению функции в этой точке, т.е. 
Пусть функция у = f(x) определена на промежутке X. Возьмем точку х  Х. Дадим значению х приращение
Х. Дадим значению х приращение  , тогда функция получит приращение
, тогда функция получит приращение  .
.
Опр. 2.2. Производной функции у = f(x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):
 .
.
Пример. 

Таблица производных:
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
6.  .
.
7. 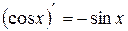 .
.
8.  .
.
9.  .
.
10.  .
.
11.  .
.
12. 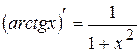 .
.
13.  .
.
Свойства производных:
Если С - постоянное число,  - функции, имеющие производные, тогда:
- функции, имеющие производные, тогда:
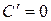 (I);
(I);
 (II);
(II);
 (III);
(III);
 (IV);
(IV);
 (V).
(V).
Пример. Вычислить производную функций.

Задача. Найти производные функции.
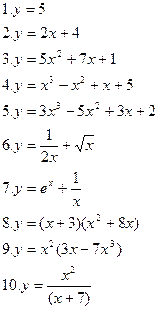
1.3. Производная сложной функции.
Исследование функции с помощью производной.
Пусть  композиция двух функций.
композиция двух функций.
Т.3.1. Если функция  дифференцируема по x, а функция
дифференцируема по x, а функция  дифференцируема по y, то сложная функция
дифференцируема по y, то сложная функция  дифференцируема по x, причем её производная вычисляется по формуле:
дифференцируема по x, причем её производная вычисляется по формуле: 
Пример. 
Задача. Найти производную сложной функции.

Опр.3.1. Точки мах и min функции называются точками экстремума функции.
Пример. Y=|x|, x=0 – точка min.
Т.3.2. пусть выполняются следующие условия:
1.  стационарная точка дифференцируемой функции, т.е.
стационарная точка дифференцируемой функции, т.е.  .
.
2. При переходе аргумента x через точку  производная меняет знак,
производная меняет знак,
Тогда точка  является точкой экстремума функции
является точкой экстремума функции 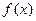 , причем:
, причем:
1) Если при переходе через точку  производная меняет знак с «-» на «+», то
производная меняет знак с «-» на «+», то  - точка минимума.
- точка минимума.
2) Если при переходе через точку  производная меняет знак с «+» на «-», то
производная меняет знак с «+» на «-», то  - точка максимума.
- точка максимума.
Пример. 
Опр. 3.2. Функция  называется выпуклой вниз на (a,b), если какова бы ни была точка
называется выпуклой вниз на (a,b), если какова бы ни была точка  , график этой функции целиком находится над графиком касательной, проходящей через эту точку.
, график этой функции целиком находится над графиком касательной, проходящей через эту точку.
Аналогично выпуклая вверх с заменой слов «над» графиком на слова «под» графиком.
Опр.3.3. Точка  называется точкой перегиба графика функции
называется точкой перегиба графика функции  , если при переходе через эту точку, функция меняет направление выпуклости.
, если при переходе через эту точку, функция меняет направление выпуклости.
Т.3.3. Пусть  дважды дифференцируема на (a,b) и точка
дважды дифференцируема на (a,b) и точка  является точкой перегиба, тогда
является точкой перегиба, тогда  .
.
Пример. 
Т.3.4. пусть точка  является корнем уравнения
является корнем уравнения  , тогда если при переходе через точку
, тогда если при переходе через точку  вторая производная меняет знак, то точка
вторая производная меняет знак, то точка  является точкой перегиба функции
является точкой перегиба функции  , причем:
, причем:
1) Если при переходе через 
 меняет знак с «-» на «+», то выпуклость вниз меняется на выпуклость вверх.
меняет знак с «-» на «+», то выпуклость вниз меняется на выпуклость вверх.
2) Если при переходе через 
 меняет знак с «+» на «-», то выпуклость вверх меняется на выпуклость вниз.
меняет знак с «+» на «-», то выпуклость вверх меняется на выпуклость вниз.
Схема исследования функции с помощью производной:
1) найти область определения функции;
2) найти точки разрыва функции и вертикальные асимптоты (если они существуют);
3) исследовать функцию на четность (нечетность) и на периодичность (для тригонометрических функций);
4) найти экстремумы и интервалы монотонности функции;
5) определить интервалы выпуклости (вогнутости) и точки перегиба;
6) исследовать поведение функции в бесконечности, найти горизонтальные и наклонные асимптоты;
7) найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.
Исследование функции проводится одновременно с построением ее графика.
Пример. Исследовать функцию  и построить ее
и построить ее
график. Решение:
1. Область определения  .
.
2. Функция непрерывна во всей ее области определения. Следовательно, нет ни точек разрыва, ни вертикальных асимптот.
3. Функция четная, так как  :
:
 .
.
График функции симметричен относительно оси ординат.
4. Экстремумы и интервалы монотонности.
 . Из уравнения
. Из уравнения  получим три критические точки:
получим три критические точки: 

 . Исследуем характер критических точек. Для этого методом пробных точек определяем знак производной в каждом из интервалов: (- ∞; -1), (-1; 0), (0; 1), (1; + ∞).
. Исследуем характер критических точек. Для этого методом пробных точек определяем знак производной в каждом из интервалов: (- ∞; -1), (-1; 0), (0; 1), (1; + ∞).

На интервалах (-∞; -1) и (0; 1) функция убывает, на интервалах (-1; 0) и (1; +∞) - возрастает. При переходе через критические точки x1 = -1 и х3 = 1 производная меняет знак с минуса на плюс, следовательно, в этих точках функция имеет минимум.  ;
; 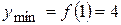 . При переходе через критическую точку х = 0 производная меняет знак с плюса на минус. Следовательно, в этой точке функция имеет максимум уmax = ƒ(0)=5.
. При переходе через критическую точку х = 0 производная меняет знак с плюса на минус. Следовательно, в этой точке функция имеет максимум уmax = ƒ(0)=5.
5. Интервалы выпуклости и точки перегиба.
 . Из уравнения
. Из уравнения 
получим  и
и  . Определяем знак второй производной в каждом из интервалов:
. Определяем знак второй производной в каждом из интервалов:
 ,
,  ,
,  .
.

Таким образом, кривая, вогнутая на интервалах  и
и  и выпуклая на интервале
и выпуклая на интервале  , а
, а  ,
,  - точки перегиба.
- точки перегиба.
 ;
;
 .
.
6. Наклонная асимптота имеет вид у = kx + b, если существуют конечные пределы:  ,
,  ;
;
 .
.
Таким образом, функция не имеет наклонных асимптот.
7. Дополнительные точки, уточняющие график:
 ;
;  . Построим график функции:
. Построим график функции:

Задачи.
1. Вычислить производные.

2. Построить график функции.

Интегральное исчисление
- Первообразная функции
Опр. 4.1.
Функция F(x) над первообразной функции F(x) на некотором промежутке, если для всех x из этого промежутка 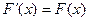
Пр: 1) F(x)=sin x – первообр. F(x)=cosx, т.к. 
2)  - первооб.
- первооб.  ,т.к
,т.к  .
.
Задача Док – ть, что F(x) – первооб. F(x)
1.  3.
3. 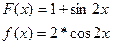
2.  4.
4. 
§1.5 Неопределенный  . Его свойства.
. Его свойства.
Опр. 5.1. Интегрирование – это процесс нахождения первообразованых
Опр. 5.2. Множество первообразованых для данной функции F(x) над неопределенным интегралом и обозначается 
Пр. 

Таблица неопределенных интегралов
-
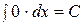 .
. -
 .
. -

 .
. -
 .
. -

 .
. -
 .
. -
 .
. -
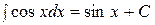 .
. -
 .
. -
 .
. -
 .
.
12.  .
.
13.  .
.
14. 
Свойства неопределенного интеграла:
- Если
 – постоянная величина, то
– постоянная величина, то  .
. -

-
 .
. -
 .
. -
 .
.
Задача: Вычислить неопределенный интеграл.

Задача. Вычислить неопределенный интеграл.

Самостоятельная работа.


Дифференциальные уравнения.
Опр.8.1. Диф.уравнением называется уравнение, связывающее функцию 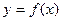 , переменную x и производную f(x).
, переменную x и производную f(x).
Опр. 8.2. Если функция 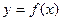 зависит только от переменной x, то диф.урав. называется обыкновенным.
зависит только от переменной x, то диф.урав. называется обыкновенным.
Общий вид обыкновенного диф.уравнения. 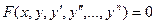 .
.
Опр. 8.3. Максимальный порядок входящих в уравнение производных называется порядком диф.уравнения.
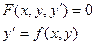 -диф.уравнение первого порядка.
-диф.уравнение первого порядка.
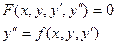 - диф. Уравнение второго порядка.
- диф. Уравнение второго порядка.
Решить диф.уравнение – значит найти первообразную функции f(x), т.е. вычислить неопределенный интеграл от F(x).
Пусть дано диф.ур. первого порядка 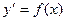 , необходимо его решить.
, необходимо его решить.
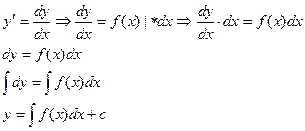 общее решение диф.уравнения.
общее решение диф.уравнения.
Алгоритм решения диф.уравнений:
1. 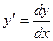
2. домножаем обе части уравнения на 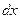 и переносим слагаемые с
и переносим слагаемые с 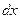 в другую сторону.
в другую сторону.
3. Переменные, содержащие x переносим к 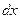 , а переменные, содержащие y к
, а переменные, содержащие y к 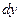 .
.
4. Интегрируем обе части уравнения.
Пример. Решить диф.уравнение.
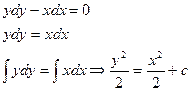
Уравнению вида 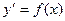 можно придать вид
можно придать вид
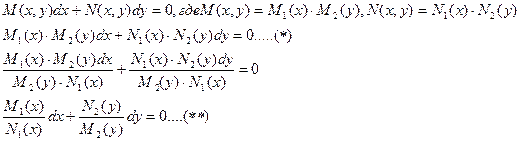
Опр.8.4. Уравнение (*) называется уравнением с разделяющимися переменными, а уравнение (**) – уравнением с разделенными переменными.
Пример. 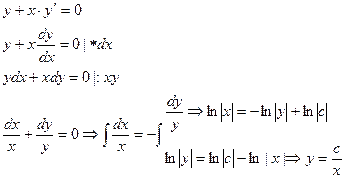
Частные производные
Дана функция двух переменных Z=F(x,y),дадим аргументу x приращение Bx, а арг. Y менять не будем, Т.Е. перейдем от точки с координатами (x,y) к точке с координатоми (x+bx,y).
Тогда функция F(x,y) получит приращение 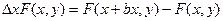 ,которое над частным приращ. Ф-ии. F(x,y) по переменой x.
,которое над частным приращ. Ф-ии. F(x,y) по переменой x.
Опр.10.1: 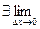
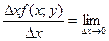
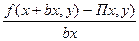
Он над частной производной ф-ии
F(x,y) и обозн. 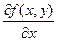
Аналогична опред-ся ч.пр. F(x,y) по Y
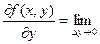
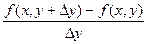
Т.Е ч.пр. 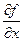 это обычная производная ф. F(x,y) по переменой x при фиксиров.знач. y, а ч.пр
это обычная производная ф. F(x,y) по переменой x при фиксиров.знач. y, а ч.пр 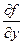 это есть обыч. Пр. Ф. F(x,y) по переменой y при фиксир. Знач. X
это есть обыч. Пр. Ф. F(x,y) по переменой y при фиксир. Знач. X
Пр; Найти ч.пр. ф-ии 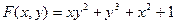
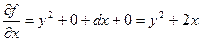
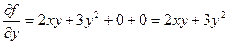
Задачи:
1. 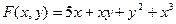 6.
6. 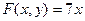
2. 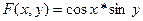 7.
7. 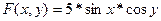
3. 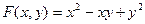 8.
8. 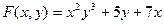
4. 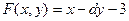 9.
9. 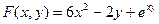
5. 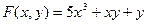 10.
10. 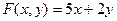
Глава 2. Ряды.
Числовые ряды.
Ряды бывают: числовые, функциональные, степенные, конечные и бесконечные, знакопеременные.
Опр.1.1. Числовым рядом называется выражение вида 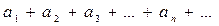 , где
, где 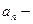 числа.
числа.
Для сокращенного обозначения рядов используют знак 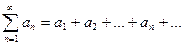
Пример. 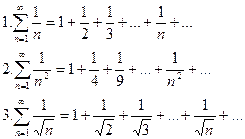
Опр. 1.2. Сумма первых n элементов ряда называется частичной суммой ряда 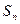 .
.
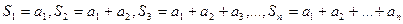
Опр. 1.3. Ряд называется сходящимся, если последовательность его частичных сумм сходится, т.е. 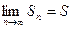 , где S – сумма ряда. (если предел не существует или равен
, где S – сумма ряда. (если предел не существует или равен 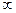 , то ряд расходится).
, то ряд расходится).
Пример. Определить сходимость ряда 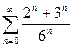 - геометрическая прогрессия.
- геометрическая прогрессия.
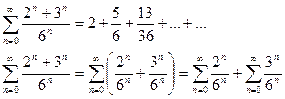
Докажем сходимость каждого ряда.
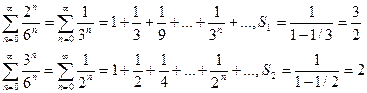
Эти ряды являются рядами бесконечной геометрической прогрессии со знаменателем <1, тогда 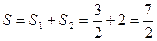 . Так как сумма ряда конечное число, то ряд сходится.
. Так как сумма ряда конечное число, то ряд сходится.
Т. 1.1. (Необходимый признак сходимости рядов).
Если ряд сходится, то его общий элемент стремится к нулю, т.е. 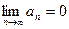 .
.
Пример. 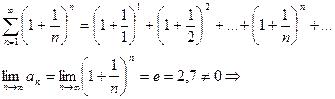 ряд расходится.
ряд расходится.
Признак Даламбера сходимости рядов.
Пусть дан ряд 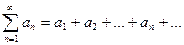 Допустим, что
Допустим, что 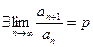 , тогда
, тогда
1) Если p<1, то ряд сходится.
2) Если p>1, то ряд расходится.
Пример. 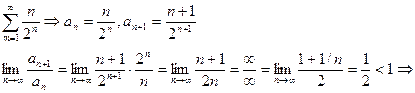 ряд сходится.
ряд сходится.
Задача. Написать первые пять элементов ряда по заданному общему элементу и проверить сходится ли ряд.
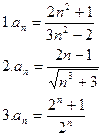
Знакопеременные ряды.
Опр.2.1. Рассмотрим ряд, у которого все элементы по очереди меняют знак: 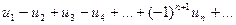 , где
, где 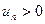 . Такой ряд называется знакочередующимся.
. Такой ряд называется знакочередующимся.
Пример. 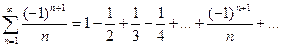
Т.2.1. (Признак Лейбница).
Пусть знакочередующийся ряд удовлетворяет следующим условиям:
- Все элементы ряда убывают
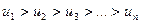 .
. - Общий элемент ряда стремится к 0 при
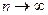 .
.
Тогда ряд сходится.
Функциональные ряды.
Опр. 3.1. Пусть дана бесконечная последовательность функций 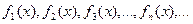 , где все функции определены на некотором множестве, тогда ряд
, где все функции определены на некотором множестве, тогда ряд 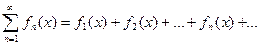 называется функциональным рядом.
называется функциональным рядом.
Если вместо аргумента x поставить конкретное число, то получим числовой ряд 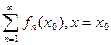 .
.
Опр. 3.2. Если этот ряд сходится, то точка 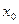 называется точкой сходимости ряда.
называется точкой сходимости ряда.
Опр. 3.3. совокупность всех точек сходимости ряда называется областью сходимости ряда.
Факториал! n!=1*2*3*4*…*n
3!=1*2*3
2!=1*2
1!=1
0!=1
Пример. 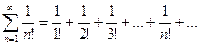
Определить сходимость данного ряда по признаку Даламбера.
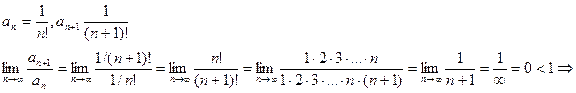 ряд сходится.
ряд сходится.
Задача. Определить сходимость ряда.
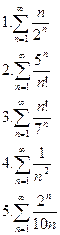
Контрольная работа по трем темам: производная, ряды, диф.уравнения.
Множества и отношения.
Опр. 1.1. Множество это совокупность объектов, которые объединены как-либо свойствами.

1. Z - Множество целых чисел 
2. Q - Множество рациональных чисел 
3. N - Натуральные числа (1,2,3…)
4. R - Действительные числа
5. C - Комплексные числа
Опр.1.2. Подмножеством В данного множества А называется множество, которое содержит некоторые элементы мн. А или множество, каждый элемент которого принадлежит мн.А.
Обозн. 
Пустое множество это множество, которое не содержит ни одного элемента.
Обозн.  Ø
Ø
Опр.1.3. пересечением двух множеств А и В называется множество, каждый элемент которого принадлежит одновременно и множеству А, и множеству В.
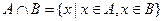
Опр. 1.4. Объединением двух множеств А и В называется множество, каждый элемент которого принадлежит или множеству А, или множеству В, или одновременно двум множествам.

Опр.1.5. Разностью множеств А и В называется множество только тех элементов множества А, которые не принадлежат В.

Опр.1.6.  . Дополнением множества В до множества А называется множество таких элементов, которые принадлежат А, и не принадлежат В.
. Дополнением множества В до множества А называется множество таких элементов, которые принадлежат А, и не принадлежат В.

Пример. А={0,1,2,…,9}, В={5,6,7,…,15}, C={0,1,2,…,15}
Найти 
Операции над множествами можно проиллюстрировать с помощью диаграмм Эйлера.






Опр. 1.7. Два множества А и В называются равными, если каждый элемент множества А принадлежит В и наоборот.
Задача 1. С помощью диаграмм Эйлера найти
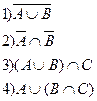
Задача 2. А={0,1,2,3,4,5,6}, B={1,2,3,4,6,8}, C={-1,0,3,4,7,8}
Найти 
Самостоятельно
А={0,1,2,3}, B={-1,2,3,4,5,6}
Найти 
Список литературы
1. Виноградов И. М.Элементы высшей математики. - М: Высш. шк., 2007.
2. Григорьев В.П. Элементы высшей математики. - М: Высш. шк., 2008
3. Григорьев С.Г. Математика: учебник для студентов сред. проф.
учреждений / С.Г. Григорьев, С.В. Задулина; под ред. В.А. Гусева. – 2-е
изд., стер. – М.: Издательский центр «Академия», 2007. – 384 с.
4. Письменный Д.Т. Конспект лекций по высшей математике: полный курс,
4-е изд. — М.: Айрис-пресс, 2008.
5. Спирина. М.С. Теория вероятностей и математическая статистика:
учебник для студ. учреждений сред. проф. образования / М.С. Спирина,
П.А. Спирин. – М.: Издательский центр «Академия», 2007. – 352 с.
6. Шипачев В. Основы высшей математики: учебное пособие для ВТУЗов. –
М: Высш. шк., 2007
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
СТАРООСКОЛЬСКИЙ ФИЛИАЛ
ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ
ВЫСШЕГО ОБРАЗОВАНИЯ
«РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГЕОЛОГОРАЗВЕДОЧНЫЙ УНИВЕРСИТЕТ
Имени СЕРГО ОРДЖОНИКИДЗЕ»
СОФ МГРИ
Г.Н.ЗУБКОВА
Н.С.ГАВРЮШКИНА
МАТЕМАТИКА
Методические указания для практических занятий и самостоятельной работы студентов 2 курса.
Старый Оскол
2018
Рецензент
СТИ НИТУ МИСиС , доцент, кандидат технических наук О.С. Кравцова
Краткая аннотация:
Методические указания являются частью основной профессиональной образовательной программы для студентов 2 курса всех специальностей в соответствии с требованиями ФГОС СПО.
Методические указания адресованы студентам очной формы обучения.
Целью данного пособия является помощь студентам выработать навыки решения практических задач по математике.
Оно включает в себя основной теоретический материал и образцы решения типовых задач.
Пособие будет полезно тем студентам, которые по различным причинам не смогли посетить все учебные занятия.
Также оно будет полезно для подготовки к практическим занятиям, для более успешного понимания и усвоения материала.
Издается по решению
ПЦК математики,физики и информатики
Протокол № от __ _ 2018 г.
Председатель ПЦК: ____ _______
Г.Н.Зубкова
Количество страниц:_______
Количество условных печатных листов:_______
Оглавление
1. Глава 1. Математический анализ………………………3
1.1. Предел функции……………………………………3
1.2. Производная функции……………………………..7
1.3. Производная сложной функции……………..…..10
1.4 Интегральное исчисление………………………...16
1.5 Неопределенный  . Его свойства………………17
. Его свойства………………17
1.6. Определенный интеграл. Вычисление
площадей плоских фигур……………………………..21
1.7. Метод замены переменной
(метод подстановки)………………………………22
1.8. Дифференциальные уравнения…………………..23
1.9. Однородные дифференциальные
уравнения первого порядка………………………..25
1.10 Частные производные…………………………….27
2. Глава 2. Ряды……………………………………………28
2.1. Числовые ряды……………………………………..28
2.2. Знакопеременные ряды…………………………...31
2.3. Функциональные ряды…………………………….31
3. Глава 3. Основы дискретной математики…………….33
3.1. Множества и отношения………………………….33
4. Глава 4. Основы теории комплексных чисел…………35
4.1. Алгебраическая форма комплексного числа…….35
4.2. Геометрическое представление
комплексных чисел…………………………………….37
4.3. Показательная форма комплексного числа………39
5. Глава 5. Основы теории вероятностей………………….42
5.1. Вероятность. Случайные события…………………42
5.2. Случайная величина. Ее функция распределения..44
5.3. Математическое ожидание и дисперсия
случайной величины………………………………..45
Самостоятельные работы ………………………………..48
Контрольная работа № 1………………………………...57
Глава 1. Математический анализ.
Предел функции.
1. Определение. Таблица замечательных пределов.
Обозначения:  множество вещественных чисел.
множество вещественных чисел.
Опр. 1.1.  , допустим, что каждому значению
, допустим, что каждому значению  по какому – либо закону поставлено в соответствие
по какому – либо закону поставлено в соответствие  . Это сопоставление определяет однозначное отображение и называется функцией одной переменной с областью определения X и множеством значений Y.
. Это сопоставление определяет однозначное отображение и называется функцией одной переменной с областью определения X и множеством значений Y.
Обозн. 
Пример.

Пусть  определена в некоторой окрестности точки а.
определена в некоторой окрестности точки а.
Опр. 1.2. число b называется пределом функции  при
при  , если для любой последовательности аргументов
, если для любой последовательности аргументов 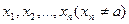 сходящихся к а, соответствующая последовательность значений функций
сходящихся к а, соответствующая последовательность значений функций  сходится у b.
сходится у b.
Обозн. 
Таблица пределов:

Свойства пределов:
1)  ;
;
2)  ;
;
3) 
|
|
|



 . Его свойства………………17
. Его свойства………………17 множество вещественных чисел.
множество вещественных чисел. , допустим, что каждому значению
, допустим, что каждому значению  по какому – либо закону поставлено в соответствие
по какому – либо закону поставлено в соответствие  . Это сопоставление определяет однозначное отображение и называется функцией одной переменной с областью определения X и множеством значений Y.
. Это сопоставление определяет однозначное отображение и называется функцией одной переменной с областью определения X и множеством значений Y.

 определена в некоторой окрестности точки а.
определена в некоторой окрестности точки а. , если для любой последовательности аргументов
, если для любой последовательности аргументов 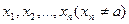 сходящихся к а, соответствующая последовательность значений функций
сходящихся к а, соответствующая последовательность значений функций  сходится у b.
сходится у b.

 ;
; ;
; ;
;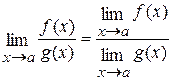 (при
(при  ).
).

 и этот предел равен значению функции в этой точке, т.е.
и этот предел равен значению функции в этой точке, т.е. 
 Х. Дадим значению х приращение
Х. Дадим значению х приращение  , тогда функция получит приращение
, тогда функция получит приращение  .
. .
.

 .
. .
. .
. .
. .
. .
.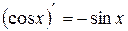 .
. .
. .
. .
. .
.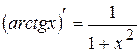 .
. .
. - функции, имеющие производные, тогда:
- функции, имеющие производные, тогда: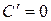 (I);
(I); (II);
(II); (III);
(III); (IV);
(IV); (V).
(V).
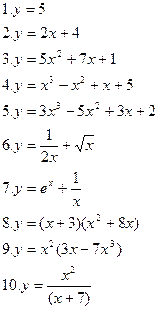
 композиция двух функций.
композиция двух функций. дифференцируема по x, а функция
дифференцируема по x, а функция  дифференцируема по y, то сложная функция
дифференцируема по y, то сложная функция  дифференцируема по x, причем её производная вычисляется по формуле:
дифференцируема по x, причем её производная вычисляется по формуле: 


 стационарная точка дифференцируемой функции, т.е.
стационарная точка дифференцируемой функции, т.е.  .
. производная меняет знак,
производная меняет знак,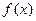 , причем:
, причем:
 называется выпуклой вниз на (a,b), если какова бы ни была точка
называется выпуклой вниз на (a,b), если какова бы ни была точка  , если при переходе через эту точку, функция меняет направление выпуклости.
, если при переходе через эту точку, функция меняет направление выпуклости. дважды дифференцируема на (a,b) и точка
дважды дифференцируема на (a,b) и точка  .
.
 меняет знак с «-» на «+», то выпуклость вниз меняется на выпуклость вверх.
меняет знак с «-» на «+», то выпуклость вниз меняется на выпуклость вверх. и построить ее
и построить ее .
. :
: .
. . Из уравнения
. Из уравнения  получим три критические точки:
получим три критические точки: 

 . Исследуем характер критических точек. Для этого методом пробных точек определяем знак производной в каждом из интервалов: (- ∞; -1), (-1; 0), (0; 1), (1; + ∞).
. Исследуем характер критических точек. Для этого методом пробных точек определяем знак производной в каждом из интервалов: (- ∞; -1), (-1; 0), (0; 1), (1; + ∞).
 ;
; 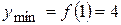 . При переходе через критическую точку х = 0 производная меняет знак с плюса на минус. Следовательно, в этой точке функция имеет максимум уmax = ƒ(0)=5.
. При переходе через критическую точку х = 0 производная меняет знак с плюса на минус. Следовательно, в этой точке функция имеет максимум уmax = ƒ(0)=5. . Из уравнения
. Из уравнения 
 и
и  . Определяем знак второй производной в каждом из интервалов:
. Определяем знак второй производной в каждом из интервалов: ,
,  ,
,  .
.
 и
и  и выпуклая на интервале
и выпуклая на интервале  , а
, а  ,
,  - точки перегиба.
- точки перегиба. ;
; .
. ,
,  ;
; .
. ;
;  . Построим график функции:
. Построим график функции:


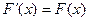

 - первооб.
- первооб.  ,т.к
,т.к  .
. 3.
3. 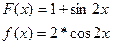
 4.
4. 
 . Его свойства.
. Его свойства.


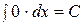 .
. .
.
 .
. .
.
 .
. .
. .
.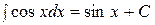 .
. .
. .
. .
. .
. .
.
 – постоянная величина, то
– постоянная величина, то  .
.
 .
. .
. .
.



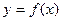 , переменную x и производную f(x).
, переменную x и производную f(x).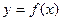 зависит только от переменной x, то диф.урав. называется обыкновенным.
зависит только от переменной x, то диф.урав. называется обыкновенным.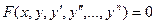 .
.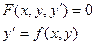 -диф.уравнение первого порядка.
-диф.уравнение первого порядка.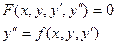 - диф. Уравнение второго порядка.
- диф. Уравнение второго порядка.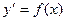 , необходимо его решить.
, необходимо его решить.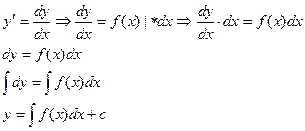 общее решение диф.уравнения.
общее решение диф.уравнения.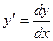
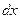 и переносим слагаемые с
и переносим слагаемые с 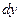 .
.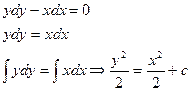
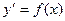 можно придать вид
можно придать вид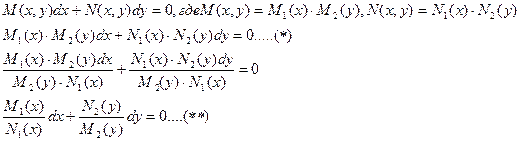
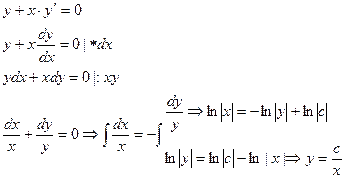
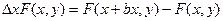 ,которое над частным приращ. Ф-ии. F(x,y) по переменой x.
,которое над частным приращ. Ф-ии. F(x,y) по переменой x.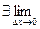
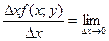
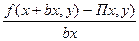
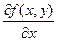
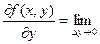
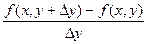
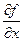 это обычная производная ф. F(x,y) по переменой x при фиксиров.знач. y, а ч.пр
это обычная производная ф. F(x,y) по переменой x при фиксиров.знач. y, а ч.пр 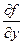 это есть обыч. Пр. Ф. F(x,y) по переменой y при фиксир. Знач. X
это есть обыч. Пр. Ф. F(x,y) по переменой y при фиксир. Знач. X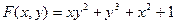
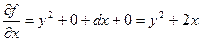
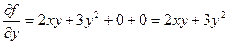
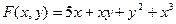 6.
6. 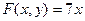
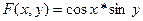 7.
7. 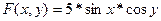
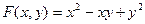 8.
8. 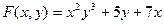
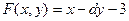 9.
9. 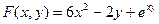
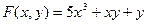 10.
10. 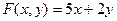
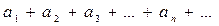 , где
, где 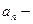 числа.
числа.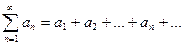
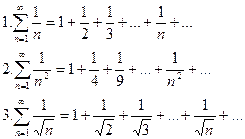
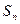 .
.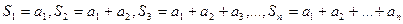
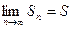 , где S – сумма ряда. (если предел не существует или равен
, где S – сумма ряда. (если предел не существует или равен 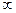 , то ряд расходится).
, то ряд расходится).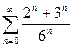 - геометрическая прогрессия.
- геометрическая прогрессия.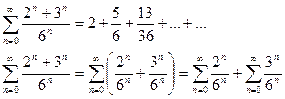
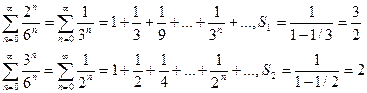
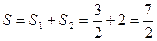 . Так как сумма ряда конечное число, то ряд сходится.
. Так как сумма ряда конечное число, то ряд сходится.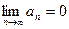 .
.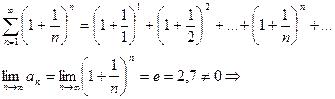 ряд расходится.
ряд расходится.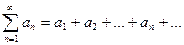 Допустим, что
Допустим, что 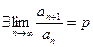 , тогда
, тогда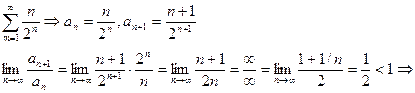 ряд сходится.
ряд сходится.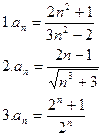
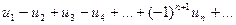 , где
, где 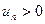 . Такой ряд называется знакочередующимся.
. Такой ряд называется знакочередующимся.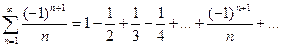
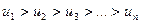 .
.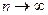 .
.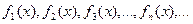 , где все функции определены на некотором множестве, тогда ряд
, где все функции определены на некотором множестве, тогда ряд 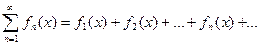 называется функциональным рядом.
называется функциональным рядом.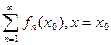 .
.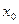 называется точкой сходимости ряда.
называется точкой сходимости ряда.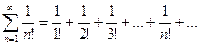
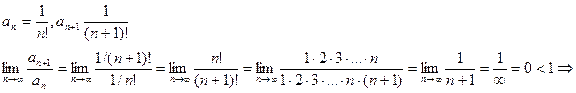 ряд сходится.
ряд сходится.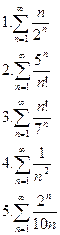




 Ø
Ø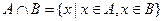


 . Дополнением множества В до множества А называется множество таких элементов, которые принадлежат А, и не принадлежат В.
. Дополнением множества В до множества А называется множество таких элементов, которые принадлежат А, и не принадлежат В.