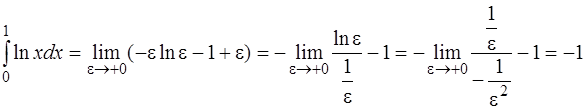ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА
Задача о площади криволинейной трапеции
Рассмотрим промежуток  и заданную на нем непрерывную неотрицательную функцию
и заданную на нем непрерывную неотрицательную функцию  . Фигура, ограниченная прямыми
. Фигура, ограниченная прямыми  и кривой
и кривой  называется криволинейной трапецией (рис. 1).
называется криволинейной трапецией (рис. 1).

Будем решать задачу о вычислении площади криволинейной трапеции.
Для этого разобьем отрезок  на части точками
на части точками  :
:
 .
.
Проведем прямые  . Тогда наша криволинейная трапеция будет представлять собой сумму
. Тогда наша криволинейная трапеция будет представлять собой сумму  узких «криволинейных полосок» (каждая k -я полоска ограничена линиями
узких «криволинейных полосок» (каждая k -я полоска ограничена линиями  ). Обозначим площадь криволинейной трапеции через
). Обозначим площадь криволинейной трапеции через  , а площадь каждой k -ой полоски через
, а площадь каждой k -ой полоски через 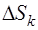 . Получим
. Получим

Площадь каждой полоски приближенно равна площади прямоугольника с основанием 
 и высотой
и высотой  , где
, где  – произвольно выбранная точка из промежутка
– произвольно выбранная точка из промежутка 
 (рис. 2). Это приближенное равенство тем ближе к точному равенству, чем уже ширина полоски
(рис. 2). Это приближенное равенство тем ближе к точному равенству, чем уже ширина полоски  .
.

Таким образом
 (1)
(1)
Введем понятие ранга дробления. Среди всех значений  выберем наибольшее, обозначим его через
выберем наибольшее, обозначим его через  и назовем рангом дробления, так что
и назовем рангом дробления, так что
 .
.
Можно показать, что в силу непрерывности функции  при
при 
 приближенное равенство (1) переходит в точное равенство
приближенное равенство (1) переходит в точное равенство
 (2)
(2)
Более того, величина  в этом случае не зависит от выбора точек
в этом случае не зависит от выбора точек  ,
,  ,
,  .
.
К необходимости изучать пределы вида (2) приводят многие задачи геометрии, механики, физики. Пределы вида (2) обобщены с помощью понятия определенного интеграла.
Свойства определенного интеграла, выражаемые неравенствами
Теорема 4. Пусть 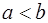 , функции
, функции  и
и  интегрируемы на промежутке
интегрируемы на промежутке  и при всех
и при всех  справедливо неравенство
справедливо неравенство
 . (11)
. (11)
Тогда
 (12)
(12)
Доказательство. Рассмотрим разность интересующих нас интегралов как интеграл разности данных функций. В силу (9)

Последний интеграл запишем по формуле (4), т.е. следуя определению определённого интеграла. Тогда получим

Здесь все парные произведения интегральной суммы неотрицательны. Действительно, по условию (11) 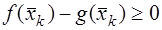 при всех
при всех  , а
, а  при всех
при всех  , поскольку
, поскольку 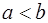 .
.
Значит и сама интегральная сумма неотрицательна. Тогда по теореме о предельном переходе в неравенстве неотрицателен и ее предел. Таким образом, получаем:
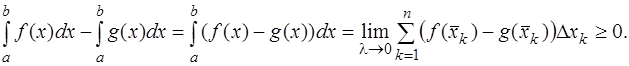
Теорема доказана.
Следствие. Пусть 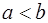 , функция
, функция  интегрируема на промежутке
интегрируема на промежутке  и при всех
и при всех  справедливо неравенство
справедливо неравенство  . Тогда
. Тогда  .
.
Теорема 5. Если функция  интегрируема на промежутке
интегрируема на промежутке  , то функция
, то функция  также интегрируема на промежутке
также интегрируема на промежутке 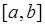 и при
и при  справедливо неравенство
справедливо неравенство
 (13)
(13)
Доказательство. Проведем его только для непрерывных функций. Заметим, что
 (14)
(14)
для всех  . К цепочке неравенств (14) применим теорему 4. Получим
. К цепочке неравенств (14) применим теорему 4. Получим
 ,
,
Что равносильно неравенству (13).
Теорема о среднем значении
Теорема 6. Пусть функции  и
и 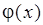 непрерывны на промежутке
непрерывны на промежутке  и пусть функция
и пусть функция 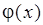 не меняет знака на этом промежутке. Тогда найдется такая точка
не меняет знака на этом промежутке. Тогда найдется такая точка  , что справедливо равенство
, что справедливо равенство
 (15)
(15)
Доказательство. Без ограничения общности будем считать, что  , а
, а  при
при  . Рассмотрим два случая.
. Рассмотрим два случая.
1). Пусть  при всех
при всех  . Тогда равенство (15) выполнено очевидным образом.
. Тогда равенство (15) выполнено очевидным образом.
2). Пусть  не является тождественно равной нулю. Тогда в силу непрерывности функции
не является тождественно равной нулю. Тогда в силу непрерывности функции  можем утверждать, что
можем утверждать, что

Поскольку функция  непрерывна на замкнутом промежутке
непрерывна на замкнутом промежутке  , то она достигает на этом промежутке своего наибольшего значения
, то она достигает на этом промежутке своего наибольшего значения  и своего наименьшего значения
и своего наименьшего значения  , т.е. при всех
, т.е. при всех  справедливы неравенства
справедливы неравенства
 . (16)
. (16)
Домножим неравенства (16) на положительные значения функции  и получим справедливые при всех
и получим справедливые при всех  неравенства
неравенства
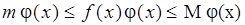 (17)
(17)
К цепочке неравенств (17) применим теорему 4 и получим справедливые неравенства
 (18)
(18)
Разделим все части цепочки неравенств (18) на положительное число  . Получим
. Получим

Поскольку непрерывная функция  принимает на промежутке
принимает на промежутке  все значения между своим наибольшим
все значения между своим наибольшим 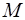 и наименьшим
и наименьшим  , существует такая точка
, существует такая точка  , что
, что

Отсюда следует, что

Таким образом, теорема 6 доказана.
Следствие. Если функция  непрерывна на промежутке
непрерывна на промежутке  , то можно указать такое значение
, то можно указать такое значение  , что
, что
 (19)
(19)
Доказательство. Будем считать  при
при 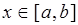 . Тогда согласно теореме 6 найдется такая точка
. Тогда согласно теореме 6 найдется такая точка  , что
, что

В случае, когда  при всех
при всех  , формула (19) имеет простой геометрический смысл. Рассмотрим криволинейную трапецию, ограниченную линиями
, формула (19) имеет простой геометрический смысл. Рассмотрим криволинейную трапецию, ограниченную линиями 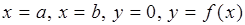 . Согласно равенству(19) площадь этой криволинейной трапеции равна площади прямоугольника с основанием
. Согласно равенству(19) площадь этой криволинейной трапеции равна площади прямоугольника с основанием  и высотой
и высотой 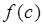 (рис. 4).
(рис. 4).

Теорема Барроу
Рассмотрим определенный интеграл с переменным верхним пределом
 (20)
(20)
Здесь  – число,
– число,  – переменная. Таким образом,
– переменная. Таким образом,  является функцией верхнего предела
является функцией верхнего предела  .
.
В силу геометрического смысла определённого интеграла, если  ,
,  , то величина
, то величина  является площадью криволинейной трапеции, ограниченной справа прямой
является площадью криволинейной трапеции, ограниченной справа прямой  . Т.к.
. Т.к.  – переменная, то и интеграл (20) изображает трапецию с переменной площадью (рис. 5).
– переменная, то и интеграл (20) изображает трапецию с переменной площадью (рис. 5).

Справедливо следующее важное утверждение.
Теорема Барроу. Если функция  непрерывна, то
непрерывна, то

т.е. производная определенного интеграла по переменному верхнему пределу равна значению подынтегральной функции в точке дифференцирования.
Доказательство. По определению производной
 ,
,
где
 . (21)
. (21)
Во втором слагаемом правой части (21) поменяем пределы интегрирования по формуле (6) и на основании теоремы 3 получим:

Величина  является площадью заштрихованной криволинейной трапеции (рис. 5). Поскольку функция
является площадью заштрихованной криволинейной трапеции (рис. 5). Поскольку функция  непрерывна, по теореме 6 о среднем значении найдется такая точка
непрерывна, по теореме 6 о среднем значении найдется такая точка  , для которой справедливо
, для которой справедливо

Тогда

Теорема доказана.
Приведем примеры применения теоремы Барроу.
Пример 6.1. 
Следствие. Любая непрерывная на промежутке  функция имеет на этом промежутке первообразную.
функция имеет на этом промежутке первообразную.
Действительно, если  – непрерывна, то существует
– непрерывна, то существует  . Но по теореме Барроу
. Но по теореме Барроу  , т.е.
, т.е.  – первообразная для
– первообразная для  . Таким образом,
. Таким образом,  – первообразная для
– первообразная для  .
.
Замечание. Первообразная непрерывной функции не всегда может быть выражена в терминах элементарных функций.
Замечания.
1. При решении задач обычно пользуются компактной формой (28), а не развернутой формой (27).
2. Типы функций, которые следует интегрировать по частям, такие же, как и в случае вычисления неопределенного интеграла.
3. Форма записи решения такая же, как и в случае неопределенного интеграла.
Приведем примеры.
Пример 8.1. Вычислить  .
.
Положим  . Получим
. Получим 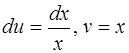 . Тогда
. Тогда
 .
.
Пример 8.2. Вычислить  .
.
Положим  . Получим
. Получим  . Тогда
. Тогда

Несобственные интегралы
Расширим понятие определенного интеграла.
1.10.1. Несобственный интеграл по бесконечному промежутку
Пусть функция 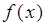 определена при всех
определена при всех  и интегрируема на каждом конечном промежутке
и интегрируема на каждом конечном промежутке  . Рассмотрим предел
. Рассмотрим предел
 (31)
(31)
Его называют интегралом функции 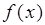 в пределах от
в пределах от  до
до  или несобственным интегралом II рода и обозначают символом
или несобственным интегралом II рода и обозначают символом
 . (32)
. (32)
Таким образом,

Если предел (31) существует и конечен, то говорят, что интеграл (32) существует или сходится. Функцию 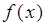 при этом называют интегрируемой на промежутке
при этом называют интегрируемой на промежутке  . Если же рассматриваемый предел (31) не существует или бесконечен, то говорят, что несобственный интеграл (32) не существует или расходится.
. Если же рассматриваемый предел (31) не существует или бесконечен, то говорят, что несобственный интеграл (32) не существует или расходится.
Пример 10.1.
 .
.
Пример 10.2.
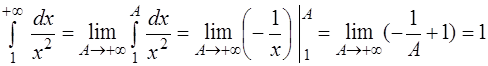 .
.
Пример 10.3.
 .
.
Таким образом, несобственный интеграл  расходится.
расходится.
Пусть теперь функция  определена на промежутке
определена на промежутке  и интегрируема на любом конечном промежутке
и интегрируема на любом конечном промежутке  . Несобственным интегралом II рода или интегралом функции
. Несобственным интегралом II рода или интегралом функции  в пределах от
в пределах от  до
до  называется
называется
 . (33)
. (33)
Этот интеграл обозначается следующим образом
 . (34)
. (34)
Таким образом,

Если предел (33) существует и конечен, то говорят, что интеграл (34) существует или сходится. Функцию 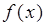 при этом называют интегрируемой на промежутке
при этом называют интегрируемой на промежутке  . В противном случае говорят, что несобственный интеграл (34) не существует или расходится.
. В противном случае говорят, что несобственный интеграл (34) не существует или расходится.
Пусть функция 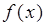 определена на всей числовой оси и интегрируема на каждом промежутке
определена на всей числовой оси и интегрируема на каждом промежутке  .
.
Тогда будем говорить, что функция 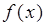 интегрируема на всей числовой оси и
интегрируема на всей числовой оси и
 , (35)
, (35)
где  – любое число, если оба интеграла в правой части (35) сходятся.
– любое число, если оба интеграла в правой части (35) сходятся.
1.10.2. Несобственный интеграл от неограниченной функции
Рассмотрим теперь конечный промежуток  , на котором функция
, на котором функция 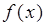 не ограничена.
не ограничена.
Пусть функция 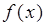 задана, ограничена и интегрируема на любом отрезке
задана, ограничена и интегрируема на любом отрезке 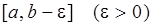 , но в точке
, но в точке  функция
функция  является бесконечно большой, т.е.
является бесконечно большой, т.е.  .
.
Рассмотрим предел
 . (36)
. (36)
Этот предел называется несобственным интегралом функции  от
от  до
до  , или несобственным интегралом I рода, и обозначается как обычно:
, или несобственным интегралом I рода, и обозначается как обычно:
 . (37)
. (37)
Если предел (36) существует и конечен, то говорят, что интеграл (37) существует, или сходится, а функция 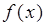 интегрируема на промежутке
интегрируема на промежутке  . Если предел (36) бесконечен или не существует, то говорят, что интеграл (37) не существует, или расходится.
. Если предел (36) бесконечен или не существует, то говорят, что интеграл (37) не существует, или расходится.
Пример 10.5.
 .
.
Пример 10.6.
 .
.
Пусть теперь функция 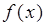 задана, ограничена и интегрируема на любом отрезке
задана, ограничена и интегрируема на любом отрезке  , но в точке
, но в точке  функция
функция  является бесконечно большой, т.е.
является бесконечно большой, т.е.  . Тогда несобственный интеграл функции
. Тогда несобственный интеграл функции  в пределах от
в пределах от  до
до  определяется равенством
определяется равенством
 (38)
(38)
Если предел, стоящий в правой части (38) существует и конечен, то говорят, что несобственный интеграл существует или сходится, а функция  интегрируема на промежутке
интегрируема на промежутке  . Если же предел бесконечен или не существует, то говорят, что интеграл не существует или расходится.
. Если же предел бесконечен или не существует, то говорят, что интеграл не существует или расходится.
Пример 10.7.

Таким образом, рассматриваемый интеграл расходится.
Теперь рассмотрим случай, когда функция 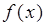 определена, ограничена и интегрируема в промежутках
определена, ограничена и интегрируема в промежутках 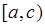 и
и  , и является бесконечно большой в точке
, и является бесконечно большой в точке  , т.е.
, т.е.  . Тогда несобственный интеграл функции
. Тогда несобственный интеграл функции  в пределах от
в пределах от  до
до  определяется равенством
определяется равенством
 (39)
(39)
Если оба предела в правой части (39) существуют и конечны при стремлении к нулю  и
и  произвольно и независимо друг от друга, то несобственный интеграл сходится. В противном случае он расходится. Сравнивая (36), (38) и (39), видим, что справедливо равенство
произвольно и независимо друг от друга, то несобственный интеграл сходится. В противном случае он расходится. Сравнивая (36), (38) и (39), видим, что справедливо равенство
 . (40)
. (40)
Несобственный интеграл в левой части (40) сходится, если сходятся оба несобственных интеграла в правой части. Если хотя бы один из интегралов справа расходится, то расходится и исходный интеграл слева.
Пример 10.11. Вычислить несобственный интеграл

или доказать его расходимость.
Решение. Подынтегральная функция стремится к  при стремлении переменной
при стремлении переменной  к нулю справа. Согласно определению
к нулю справа. Согласно определению
 .
.
Применим метод интегрирования по частям, выбрав  , и вычислим
, и вычислим

Вычисляя предел полученного выражения, воспользуемся правилом Лопиталя. Тогда
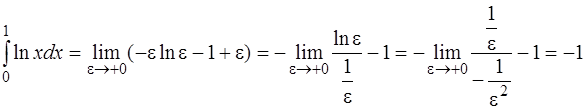
ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА



 и заданную на нем непрерывную неотрицательную функцию
и заданную на нем непрерывную неотрицательную функцию  . Фигура, ограниченная прямыми
. Фигура, ограниченная прямыми  и кривой
и кривой  называется криволинейной трапецией (рис. 1).
называется криволинейной трапецией (рис. 1).
 на части точками
на части точками  :
: .
. . Тогда наша криволинейная трапеция будет представлять собой сумму
. Тогда наша криволинейная трапеция будет представлять собой сумму  узких «криволинейных полосок» (каждая k -я полоска ограничена линиями
узких «криволинейных полосок» (каждая k -я полоска ограничена линиями  ). Обозначим площадь криволинейной трапеции через
). Обозначим площадь криволинейной трапеции через  , а площадь каждой k -ой полоски через
, а площадь каждой k -ой полоски через 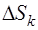 . Получим
. Получим

 и высотой
и высотой  , где
, где  – произвольно выбранная точка из промежутка
– произвольно выбранная точка из промежутка 

 (1)
(1) выберем наибольшее, обозначим его через
выберем наибольшее, обозначим его через  и назовем рангом дробления, так что
и назовем рангом дробления, так что .
.
 приближенное равенство (1) переходит в точное равенство
приближенное равенство (1) переходит в точное равенство (2)
(2) ,
,  ,
,  .
.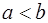 , функции
, функции  и
и  интегрируемы на промежутке
интегрируемы на промежутке  и при всех
и при всех  справедливо неравенство
справедливо неравенство . (11)
. (11) (12)
(12)

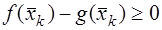 при всех
при всех  , а
, а  при всех
при всех  , поскольку
, поскольку 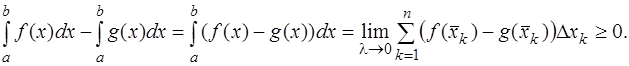
 . Тогда
. Тогда  .
. , то функция
, то функция  также интегрируема на промежутке
также интегрируема на промежутке 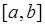 и при
и при  справедливо неравенство
справедливо неравенство (13)
(13) (14)
(14) ,
,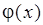 непрерывны на промежутке
непрерывны на промежутке  и пусть функция
и пусть функция  , что справедливо равенство
, что справедливо равенство (15)
(15) , а
, а  при
при  . Рассмотрим два случая.
. Рассмотрим два случая. при всех
при всех  не является тождественно равной нулю. Тогда в силу непрерывности функции
не является тождественно равной нулю. Тогда в силу непрерывности функции 
 непрерывна на замкнутом промежутке
непрерывна на замкнутом промежутке  , то она достигает на этом промежутке своего наибольшего значения
, то она достигает на этом промежутке своего наибольшего значения  и своего наименьшего значения
и своего наименьшего значения  , т.е. при всех
, т.е. при всех  . (16)
. (16) и получим справедливые при всех
и получим справедливые при всех  неравенства
неравенства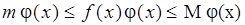 (17)
(17) (18)
(18) . Получим
. Получим
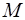 и наименьшим
и наименьшим  , существует такая точка
, существует такая точка  , что
, что

 (19)
(19) при
при 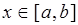 . Тогда согласно теореме 6 найдется такая точка
. Тогда согласно теореме 6 найдется такая точка 
 при всех
при всех 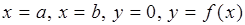 . Согласно равенству(19) площадь этой криволинейной трапеции равна площади прямоугольника с основанием
. Согласно равенству(19) площадь этой криволинейной трапеции равна площади прямоугольника с основанием  и высотой
и высотой 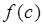 (рис. 4).
(рис. 4).
 (20)
(20) – число,
– число,  – переменная. Таким образом,
– переменная. Таким образом,  является функцией верхнего предела
является функцией верхнего предела  ,
,  , то величина
, то величина  является площадью криволинейной трапеции, ограниченной справа прямой
является площадью криволинейной трапеции, ограниченной справа прямой  . Т.к.
. Т.к. 

 ,
, . (21)
. (21)
 является площадью заштрихованной криволинейной трапеции (рис. 5). Поскольку функция
является площадью заштрихованной криволинейной трапеции (рис. 5). Поскольку функция  , для которой справедливо
, для которой справедливо


 . Но по теореме Барроу
. Но по теореме Барроу  , т.е.
, т.е.  – первообразная для
– первообразная для  . Таким образом,
. Таким образом,  .
. . Получим
. Получим 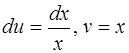 . Тогда
. Тогда .
. .
. . Получим
. Получим  . Тогда
. Тогда
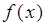 определена при всех
определена при всех  . Рассмотрим предел
. Рассмотрим предел (31)
(31)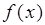 в пределах от
в пределах от  до
до  или несобственным интегралом II рода и обозначают символом
или несобственным интегралом II рода и обозначают символом . (32)
. (32)
 . Если же рассматриваемый предел (31) не существует или бесконечен, то говорят, что несобственный интеграл (32) не существует или расходится.
. Если же рассматриваемый предел (31) не существует или бесконечен, то говорят, что несобственный интеграл (32) не существует или расходится. .
.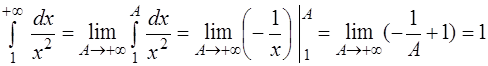 .
. .
. расходится.
расходится. определена на промежутке
определена на промежутке  и интегрируема на любом конечном промежутке
и интегрируема на любом конечном промежутке  . Несобственным интегралом II рода или интегралом функции
. Несобственным интегралом II рода или интегралом функции  в пределах от
в пределах от  до
до  называется
называется . (33)
. (33) . (34)
. (34)
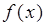 при этом называют интегрируемой на промежутке
при этом называют интегрируемой на промежутке  . В противном случае говорят, что несобственный интеграл (34) не существует или расходится.
. В противном случае говорят, что несобственный интеграл (34) не существует или расходится. .
. , (35)
, (35) – любое число, если оба интеграла в правой части (35) сходятся.
– любое число, если оба интеграла в правой части (35) сходятся. , на котором функция
, на котором функция 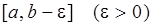 , но в точке
, но в точке  функция
функция  является бесконечно большой, т.е.
является бесконечно большой, т.е.  .
. . (36)
. (36) до
до  . (37)
. (37) . Если предел (36) бесконечен или не существует, то говорят, что интеграл (37) не существует, или расходится.
. Если предел (36) бесконечен или не существует, то говорят, что интеграл (37) не существует, или расходится. .
. .
. , но в точке
, но в точке  функция
функция  является бесконечно большой, т.е.
является бесконечно большой, т.е.  . Тогда несобственный интеграл функции
. Тогда несобственный интеграл функции  в пределах от
в пределах от  (38)
(38) . Если же предел бесконечен или не существует, то говорят, что интеграл не существует или расходится.
. Если же предел бесконечен или не существует, то говорят, что интеграл не существует или расходится.
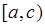 и
и  , и является бесконечно большой в точке
, и является бесконечно большой в точке  , т.е.
, т.е.  . Тогда несобственный интеграл функции
. Тогда несобственный интеграл функции  (39)
(39) и
и  произвольно и независимо друг от друга, то несобственный интеграл сходится. В противном случае он расходится. Сравнивая (36), (38) и (39), видим, что справедливо равенство
произвольно и независимо друг от друга, то несобственный интеграл сходится. В противном случае он расходится. Сравнивая (36), (38) и (39), видим, что справедливо равенство . (40)
. (40)
 к нулю справа. Согласно определению
к нулю справа. Согласно определению .
. , и вычислим
, и вычислим