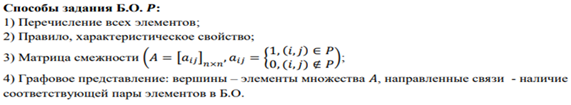Бинарные отношения и их свойства.

Бинарные отношения и их свойства.

Бинарным отношением называется любое множество упорядоченных пар. Прямого произведения двух множеств. Бинарным отношением является любое подмножество.

Пусть Р-бинарное отношение, то х, у? Р- элементы х и у связаны отношением Р.

Примеры Б.О.:

𝐴 = {1,2,3,4}, 𝑃 = {(1,2), (1,3), (2,4), (4,4)};

𝐴 = {яблоко, груша, персик, банан, киви}, 𝑃 = {(яблоко, персик), (банан, киви), (груша, киви)};

Пример: 𝐴 = {1,2,3,4}, 𝑃 = {(𝑥, 𝑦)| 𝑥 + 𝑦 > 2}. То есть (𝑥, 𝑦) ∈ 𝑃 ⇔ 𝑥 + 𝑦 > 2.

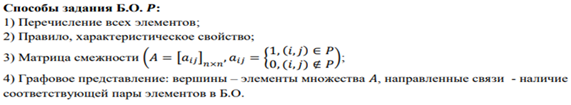
Множество – это набор (совокупность, коллекция) различимых объектов, обладающих общим для них всех характеристическим свойством.

Объекты, составляющие множество, называются его элементами.

 Примеры конечных множеств:

1. Множество цифр шестнадцатеричной системы счисления:

{0, 1,..., 9, A, B,..., F}.

2. Множество цифр двоичной системы счисления: {0, 1}.

3. Множество букв латинского алфавита:

{a, b,..., z, A, B,..., Z}.

Примеры бесконечных множеств:

4. Множество натуральных чисел: {1, 2, 3,...}.

5. Множество четных натуральных числа: {2, 4, 6,...}.

6. Множество целых чисел: {0, −1, 1, −2, 2,...}

Два множества A и B равны (обозначается A = B) тогда и только тогда, когда они состоят из одних и

Тех же элементов.

Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается ∅

Множество A содержится во множестве B (обозначение A ⊆ B) тогда и только тогда, когда каждый элемент A является элементом B.

  Пример 1.4. Пусть A = {1, 2, 3}, N= {1, 2, 3...}, тогда A ⊆ N. ¢

Иногда вместо ”A содержится в B" говорят: A включается

В B, или B содержит A, или B включает A. Если A содержится в B, то говорят, что A – подмножество B или, что то же

самое, B – надмножество A. Если A ⊆ B и существует такой

x ∈ B, что x 6 ∈ A, то говорят, что A является собственным

подмножеством B (обозначают A ⊂ B), или, что то же самое, B – собственное надмножество A. Если A не является

подмножеством B, то это обозначают так: A 6 ⊆ B.

       Теорема 1.1 Множества A и B равны тогда и только тогда, когда A ⊆ B и B ⊆ A.

Д о к а з а т е л ь с т в о (от противного).

1. ° ⇒ (необходимость). Пусть A = B. Предпол ожим, что

A 6 ⊆ B. Следовательно существует такой x, что x ∈ A, x 6 ∈ B,

Однако это противоречит тому, что множества A и B равны.

Аналогично показывается, что предположение B 6 ⊆ A также

ведет к противоречию. Следовательно, если A = B, то A ⊆

B, B ⊆ A.

  Если все множества, рассматриваемые в рамках определенной ситуации или определенного рассуждения, являются подмножествами некоторого множества U, то это множество называют универсальным множеством (универсумом) для данного рассуждения.

Примеры 1.6.

В элементарной теории чисел U – множество целых чисел

Или множество рациональных чисел.

2. Если мы рассматриваем множества, состоящие из строчных букв латинского алфавита, то U = {a, b, c,..., z}. ¢

Таким образом, на данном универсуме U множество A

задается совокупностью пар A = {hx, µA(x)i| x ∈ U}.

   Мощность множества – это обобщение понятия “число элементов” на произвольные множества.

Множество, элементами которого являются множества, называется семейством множеств

Пример 1.11.

Пусть A = {a, b, c}, тогда

B(A) = { ∅, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}. ¢

                        

Теорема Кронекера-Капелли:

Т: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Доказательство:

Необходимость

Пусть система совместна. Тогда существуют числа такие, что. Следовательно, столбец b является линейной комбинацией столбцовматрицы A. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что.

Достаточность

Пусть. Возьмем в матрице A какой-нибудь базисный минор. Так как, то он же и будет базисным минором и матрицы B. Тогда согласно теореме о базисном миноре последний столбец матрицы B будет линейной комбинацией базисных столбцов, то есть столбцов матрицы A. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы A.

Операции над матрицами.

Транспонирование.

Умножение матрицы на число.

Сложение матриц.

Умножение матриц.

Свойства обратной матрицы:

-1. Единственность: для данной матрицы А её обратная – единственная.

-2. определитель матрицы   -3. Операция взятия транспонирования и взятие матрицы обратной.

ТЕОРЕМА1: Определитель матрицы А равен сумме произведений всех элементов произвольной строки (столбца) на их алгебраические дополнения.

Бинарные отношения и их свойства.