65.1. Пусть случайная величина 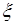 имеет плотность вероятности
имеет плотность вероятности  и функция одной переменной
и функция одной переменной  ,
,  , является взаимно однозначной, тогда плотность вероятности
, является взаимно однозначной, тогда плотность вероятности  случайной величины
случайной величины  определяется соотношением:
определяется соотношением:
 , (65.1)
, (65.1)
где  - функция, обратная функции
- функция, обратная функции  .
.
Вывод формулы (65.1) основан на соотношениях (64.4) и (64.6). Поскольку функция  - взаимно однозначная, то эта функция или монотонно возрастающая
- взаимно однозначная, то эта функция или монотонно возрастающая  или монотонно убывающая
или монотонно убывающая  . Очевидны соотношения:
. Очевидны соотношения:
 , (65.2)
, (65.2)
 . (65.3)
. (65.3)
Пусть  ,
, 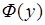 - функции распределения вероятностей случайных величин
- функции распределения вероятностей случайных величин 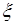 и
и 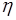 . Если
. Если  , тогда используя (65.2),
, тогда используя (65.2),
 . (65.4)
. (65.4)
Продифференцируем по  равенство (65.4), тогда
равенство (65.4), тогда
 . (65.5)
. (65.5)
Аналогично при  справедливо равенство (65.3), поэтому
справедливо равенство (65.3), поэтому
 (65.6)
(65.6)
Отсюда:
 . (65.7)
. (65.7)
Теперь из соотношений (65.5) и (65.7) следует (65.1).
Существенным условием при выводе формулы (65.1) является свойство взаимной однозначности функции  . Примерами таких функций являются: 1). Линейная функция
. Примерами таких функций являются: 1). Линейная функция  , где
, где  ,
,  - числа, при этом обратная функция имеет вид
- числа, при этом обратная функция имеет вид  ; 2). Экспонента -
; 2). Экспонента -  , откуда обратная функция
, откуда обратная функция  ,
,  , и другие. Однако условие взаимной однозначности функции
, и другие. Однако условие взаимной однозначности функции  может нарушаться, например, для функции
может нарушаться, например, для функции  обратная функция
обратная функция  ,
,  - двузначная. При этом рассматриваются две функции
- двузначная. При этом рассматриваются две функции 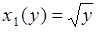 и
и  ,
, 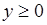 , которые называются первая и вторая ветви обратного преобразования
, которые называются первая и вторая ветви обратного преобразования 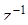 . Более сложный пример:
. Более сложный пример:  . Здесь обратная функция – многозначная.
. Здесь обратная функция – многозначная.
65.2. Рассмотрим модификацию формулы (65.1) на случай многозначного обратного преобразования  . Для этого на области определения функции
. Для этого на области определения функции  выделим неперекрывающиеся интервалы
выделим неперекрывающиеся интервалы  ,
,  - целое, на которых
- целое, на которых  , тогда на интервалах вида
, тогда на интервалах вида 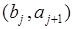 выполняется условие
выполняется условие  . Функция
. Функция  , для
, для  , монотонная возрастающая, а для
, монотонная возрастающая, а для  - монотонная убывающая. Поэтому для каждого из указанных интервалов существует однозначная обратная функция по отношению к функции
- монотонная убывающая. Поэтому для каждого из указанных интервалов существует однозначная обратная функция по отношению к функции  . Пусть функция
. Пусть функция  для
для  имеет обратную функцию вида
имеет обратную функцию вида  ,
,  , очевидно
, очевидно  - монотонная возрастающая, поскольку обратная ей
- монотонная возрастающая, поскольку обратная ей  - монотонная возрастающая. Аналогично обозначим через
- монотонная возрастающая. Аналогично обозначим через  - функцию со значениями
- функцию со значениями  , обратную к
, обратную к  на интервале
на интервале  . Очевидно
. Очевидно  - монотонная убывающая. Функция
- монотонная убывающая. Функция  называется
называется  -я ветвь обратного преобразования функции
-я ветвь обратного преобразования функции  . Теперь по формуле сложения вероятностей для несовместных событий:
. Теперь по формуле сложения вероятностей для несовместных событий:
 (65.8)
(65.8)
где суммирование ведется по всем ветвям обратного преобразования.
На рис. 65.1. представлен простой пример функции 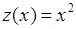 , у которой ветви обратного преобразования:
, у которой ветви обратного преобразования:  со значениями
со значениями 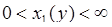 , и
, и  - со значениями
- со значениями 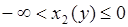 . На интервале
. На интервале  функция
функция  - монотонно возрастающая, а на интервале
- монотонно возрастающая, а на интервале 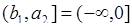 функция
функция  - монотонная убывающая. Равенство (65.8) в этом случае принимает вид:
- монотонная убывающая. Равенство (65.8) в этом случае принимает вид:
 .
.

Рис. 65.1. Пример преобразования случайной величины.
Представим вероятности в (65.8) через плотности вероятностей, тогда:
 . (65.9)
. (65.9)
Дифференцируя по  обе части (65.9), получим
обе части (65.9), получим
 (65.10)
(65.10)
или
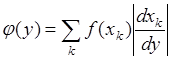 , (65.11)
, (65.11)
где суммирование по 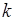 ведется по всем ветвям обратного преобразования.
ведется по всем ветвям обратного преобразования.
65.3. Рассмотрим примеры вычисления плотности вероятности случайной величины  по формуле (65.11). Пусть
по формуле (65.11). Пусть 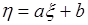 - линейное преобразование случайной величины
- линейное преобразование случайной величины 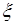 . Функция
. Функция  - взаимно однозначная, поэтому обратное преобразование имеет одну ветвь и сумма в (65.11) содержит одно слагаемое. Поскольку
- взаимно однозначная, поэтому обратное преобразование имеет одну ветвь и сумма в (65.11) содержит одно слагаемое. Поскольку  , то (65.11) принимает вид:
, то (65.11) принимает вид:
 . (65.12)
. (65.12)
Рассмотрим квадратичное преобразование 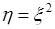 . Обратное преобразование имеет две ветви
. Обратное преобразование имеет две ветви  и
и 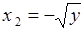 . Поэтому сумма (65.11) состоит из двух слагаемых. Вычисляя,
. Поэтому сумма (65.11) состоит из двух слагаемых. Вычисляя,  для
для  , получаем:
, получаем:
 (65.13)
(65.13)
Пусть  и случайная величина
и случайная величина 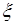 имеет равномерное распределение вероятностей на интервале
имеет равномерное распределение вероятностей на интервале  , с плотностью
, с плотностью  , если
, если  , и
, и  при
при  . Обратное преобразование имеет две ветви:
. Обратное преобразование имеет две ветви:  , а также
, а также 
 . Вычисление производных
. Вычисление производных  и подстановка в (65.11) приводит к результату:
и подстановка в (65.11) приводит к результату:
 . (65.14)
. (65.14)
На рис. 65.2. представлен график плотности  косинус-преобразования
косинус-преобразования
равномерно распределенной случайной величины. Таким образом, исходная

Рис. 65.2. Плотность вероятности косинус-преобразования.
исходная величина 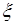 и преобразованная величина
и преобразованная величина  могут иметь совершенно непохожие плотности вероятности.
могут иметь совершенно непохожие плотности вероятности.
Преобразование нескольких случайных величин
66.1. Соотношение (65.11), определяющее плотность вероятности  преобразованной величины
преобразованной величины  через плотность
через плотность 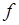 исходной случайной величины
исходной случайной величины 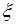 , можно обобщить на случай преобразования
, можно обобщить на случай преобразования  случайных величин. Пусть случайные величины
случайных величин. Пусть случайные величины  имеют совместную плотность
имеют совместную плотность 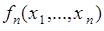 , и заданы
, и заданы  функций
функций  ,
,  переменных
переменных 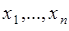 . Необходимо найти совместную плотность вероятности
. Необходимо найти совместную плотность вероятности  случайных величин:
случайных величин:
 (66.1)
(66.1)
Эта задача отличается от общей постановки, п. 6.4., условием  - число исходных случайных величин равно числу преобразованных величин. Преобразование, обратное (66.1), находится как решение системы уравнений
- число исходных случайных величин равно числу преобразованных величин. Преобразование, обратное (66.1), находится как решение системы уравнений  ,
,  , относительно переменных
, относительно переменных  . При этом каждое
. При этом каждое  зависит от
зависит от  . Совокупность таких функций
. Совокупность таких функций  ,
, 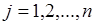 , образует обратное преобразование. В общем случае обратное преобразование неоднозначно. Пусть
, образует обратное преобразование. В общем случае обратное преобразование неоднозначно. Пусть  ,
,  , -
, -  - я ветвь обратного преобразования
- я ветвь обратного преобразования  , тогда справедливо соотношение:
, тогда справедливо соотношение:
 , (66.2)
, (66.2)
где сумма берется по всем ветвям обратного преобразования,
 (66.3)
(66.3)
- якобиан преобразования от случайных величин  к случайным величинам
к случайным величинам 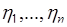 .
.
Если из каждой совокупности  случайных величин получается
случайных величин получается  случайных величин
случайных величин  , то формулой (66.2) можно воспользоваться, дополнив систему
, то формулой (66.2) можно воспользоваться, дополнив систему  до
до  случайных величин, например, такими величинами
случайных величин, например, такими величинами  . Если же
. Если же  , то
, то  случайных величин из совокупности
случайных величин из совокупности 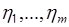 функционально связаны с остальными
функционально связаны с остальными  величинами, поэтому
величинами, поэтому 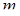 - мерная плотность
- мерная плотность  будет содержать
будет содержать  дельта-функций.
дельта-функций.
Соотношения (64.4), (64.6) и (66.2) определяют два метода решения задачи вычисления плотности  совокупности случайных величин
совокупности случайных величин  , полученных функциональным преобразованием исходных случайных величин
, полученных функциональным преобразованием исходных случайных величин  с совместной плотностью вероятности
с совместной плотностью вероятности  . Основная трудность в применении первого метода состоит в вычислении
. Основная трудность в применении первого метода состоит в вычислении  -мерного интеграла по сложной области
-мерного интеграла по сложной области  . Во втором методе основная трудность – это нахождение всех ветвей обратного преобразования.
. Во втором методе основная трудность – это нахождение всех ветвей обратного преобразования.
66.2. Рассмотрим простой пример вычисления плотности вероятности суммы двух случайных величин  и
и  с плотностью
с плотностью 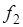 по формуле (66.2). Очевидно, в качестве первой преобразованной величины следует выбрать сумму:
по формуле (66.2). Очевидно, в качестве первой преобразованной величины следует выбрать сумму: 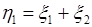 , а в качестве второй
, а в качестве второй  (хотя можно взять и
(хотя можно взять и  ). Таким образом, функциональное преобразование от
). Таким образом, функциональное преобразование от  ,
,  к
к  ,
,  задается системой уравнений:
задается системой уравнений:
 (66.4)
(66.4)
Обратное преобразование – это решение системы уравнений относительно  ,
,  :
:
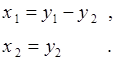 (66.5)
(66.5)
Обратное преобразование однозначно, поэтому в (66.2) сумма состоит из одного слагаемого. Найдем якобиан преобразования:
 .
.
Теперь (66.2) для  принимает вид:
принимает вид:
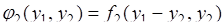 . (66.6)
. (66.6)
Функция  - это совместная плотность вероятности случайных величин
- это совместная плотность вероятности случайных величин  и
и  . Отсюда плотность вероятности
. Отсюда плотность вероятности 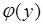 суммы
суммы  находится из условия согласованности:
находится из условия согласованности:
 . (66.7)
. (66.7)
Рассмотрим первый метод решения этой же задачи. Из (64.4) следует:
 . 66.8)
. 66.8)
Задача сводится к преобразованию интеграла по области  , определяемой условием
, определяемой условием  . Этот интеграл можно представить в виде:
. Этот интеграл можно представить в виде:
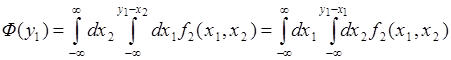 (66.9)
(66.9)
Отсюда плотность вероятности:
Отсюда плотность вероятности:
 , (66.10)
, (66.10)
что совпадает с формулой (66.7).



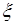 имеет плотность вероятности
имеет плотность вероятности  и функция одной переменной
и функция одной переменной  ,
,  , является взаимно однозначной, тогда плотность вероятности
, является взаимно однозначной, тогда плотность вероятности  случайной величины
случайной величины  определяется соотношением:
определяется соотношением: , (65.1)
, (65.1) - функция, обратная функции
- функция, обратная функции  .
. - взаимно однозначная, то эта функция или монотонно возрастающая
- взаимно однозначная, то эта функция или монотонно возрастающая  или монотонно убывающая
или монотонно убывающая  . Очевидны соотношения:
. Очевидны соотношения: , (65.2)
, (65.2) . (65.3)
. (65.3) ,
, 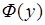 - функции распределения вероятностей случайных величин
- функции распределения вероятностей случайных величин 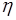 . Если
. Если  , тогда используя (65.2),
, тогда используя (65.2), . (65.4)
. (65.4) равенство (65.4), тогда
равенство (65.4), тогда . (65.5)
. (65.5) справедливо равенство (65.3), поэтому
справедливо равенство (65.3), поэтому (65.6)
(65.6) . (65.7)
. (65.7) , где
, где  ,
,  - числа, при этом обратная функция имеет вид
- числа, при этом обратная функция имеет вид  ; 2). Экспонента -
; 2). Экспонента -  , откуда обратная функция
, откуда обратная функция  ,
,  , и другие. Однако условие взаимной однозначности функции
, и другие. Однако условие взаимной однозначности функции  обратная функция
обратная функция  ,
,  - двузначная. При этом рассматриваются две функции
- двузначная. При этом рассматриваются две функции 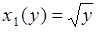 и
и  ,
, 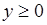 , которые называются первая и вторая ветви обратного преобразования
, которые называются первая и вторая ветви обратного преобразования 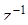 . Более сложный пример:
. Более сложный пример:  . Здесь обратная функция – многозначная.
. Здесь обратная функция – многозначная. . Для этого на области определения функции
. Для этого на области определения функции  выделим неперекрывающиеся интервалы
выделим неперекрывающиеся интервалы  ,
,  - целое, на которых
- целое, на которых  , тогда на интервалах вида
, тогда на интервалах вида 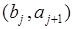 выполняется условие
выполняется условие  . Функция
. Функция  , монотонная возрастающая, а для
, монотонная возрастающая, а для  - монотонная убывающая. Поэтому для каждого из указанных интервалов существует однозначная обратная функция по отношению к функции
- монотонная убывающая. Поэтому для каждого из указанных интервалов существует однозначная обратная функция по отношению к функции  . Пусть функция
. Пусть функция  имеет обратную функцию вида
имеет обратную функцию вида  ,
,  , очевидно
, очевидно  - монотонная возрастающая, поскольку обратная ей
- монотонная возрастающая, поскольку обратная ей  - функцию со значениями
- функцию со значениями  , обратную к
, обратную к  на интервале
на интервале  . Очевидно
. Очевидно  называется
называется  (65.8)
(65.8)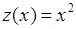 , у которой ветви обратного преобразования:
, у которой ветви обратного преобразования:  со значениями
со значениями 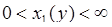 , и
, и  - со значениями
- со значениями 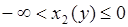 . На интервале
. На интервале  функция
функция  - монотонно возрастающая, а на интервале
- монотонно возрастающая, а на интервале 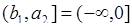 функция
функция  - монотонная убывающая. Равенство (65.8) в этом случае принимает вид:
- монотонная убывающая. Равенство (65.8) в этом случае принимает вид: .
.
 . (65.9)
. (65.9) (65.10)
(65.10)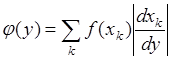 , (65.11)
, (65.11)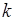 ведется по всем ветвям обратного преобразования.
ведется по всем ветвям обратного преобразования.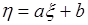 - линейное преобразование случайной величины
- линейное преобразование случайной величины  - взаимно однозначная, поэтому обратное преобразование имеет одну ветвь и сумма в (65.11) содержит одно слагаемое. Поскольку
- взаимно однозначная, поэтому обратное преобразование имеет одну ветвь и сумма в (65.11) содержит одно слагаемое. Поскольку  , то (65.11) принимает вид:
, то (65.11) принимает вид: . (65.12)
. (65.12)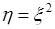 . Обратное преобразование имеет две ветви
. Обратное преобразование имеет две ветви  и
и 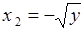 . Поэтому сумма (65.11) состоит из двух слагаемых. Вычисляя,
. Поэтому сумма (65.11) состоит из двух слагаемых. Вычисляя,  для
для  , получаем:
, получаем: (65.13)
(65.13) и случайная величина
и случайная величина  , с плотностью
, с плотностью  , если
, если  , и
, и  при
при  . Обратное преобразование имеет две ветви:
. Обратное преобразование имеет две ветви:  , а также
, а также 
 . Вычисление производных
. Вычисление производных  и подстановка в (65.11) приводит к результату:
и подстановка в (65.11) приводит к результату: . (65.14)
. (65.14)
 могут иметь совершенно непохожие плотности вероятности.
могут иметь совершенно непохожие плотности вероятности. преобразованной величины
преобразованной величины 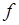 исходной случайной величины
исходной случайной величины 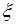 , можно обобщить на случай преобразования
, можно обобщить на случай преобразования  случайных величин. Пусть случайные величины
случайных величин. Пусть случайные величины  имеют совместную плотность
имеют совместную плотность 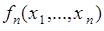 , и заданы
, и заданы  функций
функций  ,
,  переменных
переменных 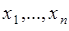 . Необходимо найти совместную плотность вероятности
. Необходимо найти совместную плотность вероятности  случайных величин:
случайных величин: (66.1)
(66.1) - число исходных случайных величин равно числу преобразованных величин. Преобразование, обратное (66.1), находится как решение системы уравнений
- число исходных случайных величин равно числу преобразованных величин. Преобразование, обратное (66.1), находится как решение системы уравнений  ,
,  , относительно переменных
, относительно переменных  . При этом каждое
. При этом каждое  зависит от
зависит от  . Совокупность таких функций
. Совокупность таких функций  ,
, 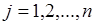 , образует обратное преобразование. В общем случае обратное преобразование неоднозначно. Пусть
, образует обратное преобразование. В общем случае обратное преобразование неоднозначно. Пусть  ,
,  , -
, -  , тогда справедливо соотношение:
, тогда справедливо соотношение: , (66.2)
, (66.2) (66.3)
(66.3) к случайным величинам
к случайным величинам 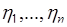 .
. случайных величин получается
случайных величин получается  случайных величин
случайных величин  , то формулой (66.2) можно воспользоваться, дополнив систему
, то формулой (66.2) можно воспользоваться, дополнив систему  до
до  . Если же
. Если же  , то
, то  случайных величин из совокупности
случайных величин из совокупности 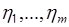 функционально связаны с остальными
функционально связаны с остальными 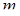 - мерная плотность
- мерная плотность  будет содержать
будет содержать  совокупности случайных величин
совокупности случайных величин  с совместной плотностью вероятности
с совместной плотностью вероятности  . Основная трудность в применении первого метода состоит в вычислении
. Основная трудность в применении первого метода состоит в вычислении  . Во втором методе основная трудность – это нахождение всех ветвей обратного преобразования.
. Во втором методе основная трудность – это нахождение всех ветвей обратного преобразования. и
и  с плотностью
с плотностью 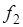 по формуле (66.2). Очевидно, в качестве первой преобразованной величины следует выбрать сумму:
по формуле (66.2). Очевидно, в качестве первой преобразованной величины следует выбрать сумму: 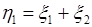 , а в качестве второй
, а в качестве второй  (хотя можно взять и
(хотя можно взять и  ). Таким образом, функциональное преобразование от
). Таким образом, функциональное преобразование от  ,
,  ,
,  задается системой уравнений:
задается системой уравнений: (66.4)
(66.4) ,
,  :
: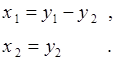 (66.5)
(66.5) .
.  принимает вид:
принимает вид: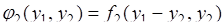 . (66.6)
. (66.6) - это совместная плотность вероятности случайных величин
- это совместная плотность вероятности случайных величин  и
и  . Отсюда плотность вероятности
. Отсюда плотность вероятности 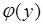 суммы
суммы  находится из условия согласованности:
находится из условия согласованности: . (66.7)
. (66.7) . 66.8)
. 66.8) , определяемой условием
, определяемой условием  . Этот интеграл можно представить в виде:
. Этот интеграл можно представить в виде: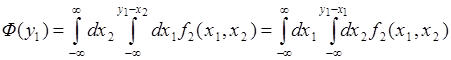 (66.9)
(66.9) , (66.10)
, (66.10)

